時速100公里級地鐵車輛通過隧道時引起的活塞風仿真研究

樸榮煥，張繼業，李田

時速100公里級地鐵車輛通過隧道時引起的活塞風仿真研究

樸榮煥，張繼業，李田

（西南交通大學 牽引動力國家重點實驗室，四川 成都 610031）

地鐵車輛通過隧道時，會誘導隧道內氣體流動，對隧道內通風、基礎設備運行以及人員安全造成安全隱患。為確保隧道內設備正常運行與人員安全，針對地鐵車通過隧道時引起的氣體流動進行研究。本文使用仿真計算的方法，基于滑動網絡技術數值模擬某一地鐵車輛通過隧道的動態過程，監測地鐵車輛通過隧道時引起的隧道內氣體流動。結果表明：隧道內活塞風縱向分量和總流量變化基本一致，隧道內的活塞風主要是縱向流;距離車體或地面越遠，列車風流速最大值越小；車底與車頂處活塞風沿垂向距離降低緩慢，車體中部活塞風流速沿垂向迅速降低；隧道內活塞風流速最大值出現在距離入口750 m處。

地鐵車輛；隧道滑流；壓力波

高速列車運行時，由于空氣的粘性，運動列車會帶動車體周圍空氣運動，稱為列車風。目前對于明線運行時車體周圍的列車風進行了廣泛研究，特別是車頭幾何形狀、列車長度、列車速度等因素對車體周圍流暢的影響[1-4]，同時有研究指出，列車風的強度在橫向和垂直方向上與車體的距離高度相關[5]。而當高速列車從外部環境進入隧道時，列車周圍的空間急劇縮小。由于隧道壁面的限制，當列車頭部進入隧道時，在車頭前方形成高壓區，產生壓縮波，推動空氣向前運動；當列車尾部進入隧道時，尾部后部會形成低壓區，產生膨脹波，將外部空氣吸入隧道，這種由運行列車所驅使的空氣運動被稱為活塞效應[6]。活塞效應引起的氣流會對隧道內的通風機、接觸網系統和橫向通道的安全門等裝置產生較大的瞬態壓力，影響設備正常運行，同時會對軌旁工作人員造成潛在的安全隱患。陳逸斐[7]通過有限元模型對地鐵車輛端部底架疲勞強度進行虛擬試驗。而針對隧道內滑流對人員及設備的危害，歐盟國家共享一套規則，指出根據列車在兩個高度（0.2 m和1.4 m）下的最大合成允許水平風速[8]；在日本，安全站立距離基于9 m/s滑流平均速度[9]；在中國，考慮到安全問題，14 m/s速度被視為滑流極限[10]。劉堂紅等[11]對隧道中的列車誘導的列車風進行了現場測量，發現流暢速度大小與列車速度呈線性關系。列車通過隧道時產生的氣流基本上是三維的，在縱向、橫向及垂向都有分量。由于隧道的縱向長度遠遠大于橫向寬度，在隧洞中傳輸的壓力波可近似視為一維平面波[12]。滑流強度與車頭流線型形狀、列車運行速度和距離車體的橫向距離有關，而地鐵車輛相較于高速列車，其頭型流線型更小且隧道直徑較小，會產生劇烈的壓力波動和氣體流動。因此為確保地鐵車隧道內的人員安全及隧道內設備的安全，需要對地鐵車通過隧道時引起的隧道內滑流進行研究。

1 仿真方法

1.1 幾何模型

地鐵車模型為六節車模型，最高運營速度為100 km/h。車輛部件包括空調、轉向架、車鉤和風擋等，如圖1所示。由于車燈等結構對此研究結果影響很小，建立幾何模型時進行了簡化處理。此模型車長為141 m，車寬為3.1 m，車高為3.8 m，縱向截面面積10.28 m2。隧道為圓形隧道，隧道截面直徑為6 m。

圖1 地鐵及其車模型

1.2 計算域及邊界條件

計算域入口與出口處采用半圓形計算域，半圓形區域半徑為50 m、長度為500 m，列車頭車距離入口距離為50 m。根據隧道內最大負壓峰值，隧道長度是列車運行的最不利長度[16-17]，計算公式為：

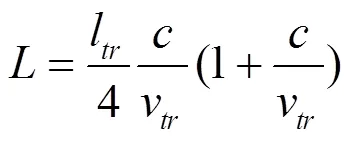
式中：l為列車長度，m；為當地聲速，m/s；v為列車列車運行速度，m/s。

計算區域分為兩個部分：區域Ⅰ為包含列車的細長半圓柱形，而區域Ⅱ包括外部區域和部分隧道區域，如圖2所示。列車與隧道的相對運動采用滑移網格實現。滑移網格法目前被證明是模擬列車通過隧道時產生的相互作用最有效方法之一[13]。與動網格相比，滑移網格不需要變化網格，在確保精度的前提下大大提高了網格質量和計算效率。區域Ⅰ與區域Ⅱ的邊界采用交界面傳輸信息。

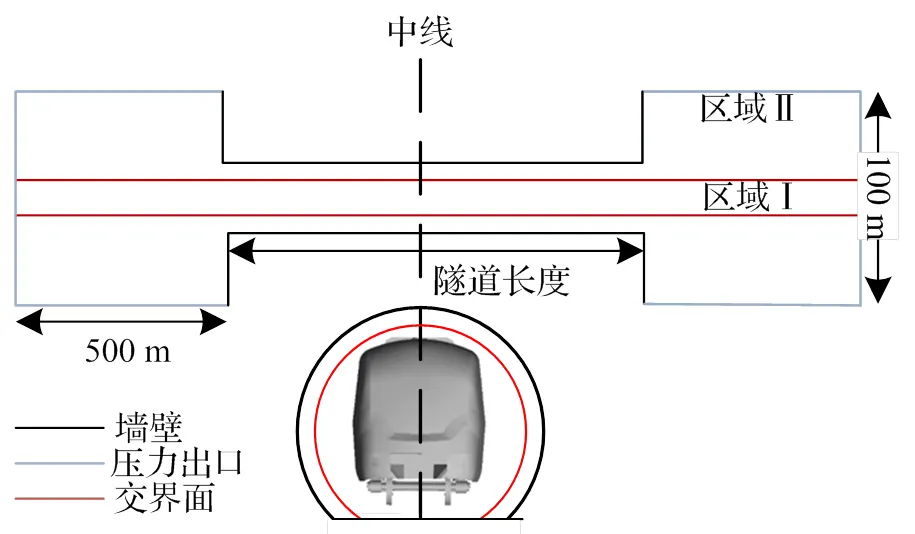
圖2 邊界條件設置

為了避免壓力波在外部邊界上的反射，將外部計算域的頂面、側面和背面定義為壓力出口。列車表面、地面和隧道表面被定義為靜止的防滑壁邊界。坐標系原點位于隧道入口地面中點，軸沿隧道縱向，軸沿隧道橫向，軸沿隧道垂向。

1.3 網格劃分

由于列車具有復雜的幾何結構，包括轉向架、空調和風擋等，因此，Ⅰ區采用四面體網格，Ⅱ區采用結構網格生成六面體網格。在網格劃分中，為了準確地模擬車體周圍的流場變化，列車附近流場區域采用四面體網格、且對曲面變化較大的部分進行加密處理。同時外部計算域靠近隧道端流場進行軸向加密處理，橫向沿指向隧道入口與隧道出口方向進行加密。網格劃分的結果如圖3所示，總網格數量約為2400萬。

圖3 計算域及車體網格

1.4 求解器

由于活塞效應，列車通過隧道時引起的氣體流動為非定常流動，氣體模型采用理想可壓縮氣體，湍流模型選擇Rng k-e。有研究證明，該方法在模擬列車通過隧道時引起的氣動效應是有效的[13-15]，在大多數情況下，相關應用和驗證的工作與移動模型或全尺寸實驗數據的最大差異都在5%以內。控制方程采用連續性方程、Navier-Stokes方程和能量方程，分別描述了質量守恒、動量守恒和能量守恒的物理關系。壁面函數采用尺度化壁面函數，采用壓力基的PISO算法依次迭代方程組中的壓力、速度項。由于高壓驅動氣流運動，采用PRESTO!算法離散壓力項，有利于捕捉初始的高、低壓界面流動。密度、動量及能量方程采用二階迎風格式。為加快收斂，采用二階隱式的對偶時間步推進方法離散時間項，以增大時間步迭代的穩定性時間步長設為0.005 s，總時間步數以頭車到達出口計算域邊界為標準，每步迭代20次。

1.5 監測點布置

監測點橫向位置以及所在的縱向平面如圖4所示，監測點距離車體中軸線分別為1.7 m、2.2 m與2.7 m。垂向距離以地面為基準，每間隔0.5 m設置一個監測點，分別位于左右兩側，監測縱向流速分量v、橫向流速分量v與垂向流速分量v。

總滑流計算式為：

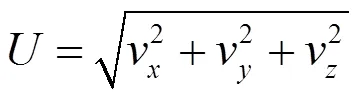
1.6 網格獨立性檢驗

綜合考慮選擇合適的網格尺寸，Mesh1采用細網格，Mesh2采用粗網格，體網格最大尺寸均為500 mm，車體面網格尺寸和總網格數量如表1所示。隧道長度采用上節提到的最不利隧道長度1075 m，對比隧道中點監測點處列車風數據，如圖5所示，可見，兩種網格計算的結果趨勢相同，尾車通過監測點時粗網格與細網兩種網格尾流流速峰值分別為21.9 m/s和22.4 m/s、誤差為2.2%，在可接受范圍內，所以后續工況采用粗網格尺寸進行模擬仿真。

表1 粗網格與細網格網格尺寸與網格數量

圖5 粗網格與細網格計算結果對比

1.7 模型驗證

文獻[16]中進行了地鐵車輛實車試驗，監測了隧道內表面氣體流速，將文獻中的結果與仿真結果進行對比，仿真結果與試驗數據相吻合，如圖6所示。由于文獻[16]中隧道內存在初始風速，而仿真中沒有考慮隧道內的初始風速，所以列車通過監測點前的結果不吻合，但當尾車通過監測點后實驗結果與仿真結果一致，可以說明此研究方法是可靠的。

圖6 仿真數據與實驗數據對比

2 結果與分析

2.1 流動方向

圖7繪制了隧道中點處縱向流速分量v、橫向流速分量v和垂向流速分量v與總流速的關系。由于總流速永遠為正值，可以看出，縱向流速分量v與總流速的絕對峰值相同，且橫向流速分量v與垂向流速分量v相對相對較小，經過平方根計算后可以忽略不計，說明隧道內的氣體流動主要為縱向流動，與文獻[12]所提出的結論相同，因此在以下的分析中，主要針對縱向滑流進行分析。

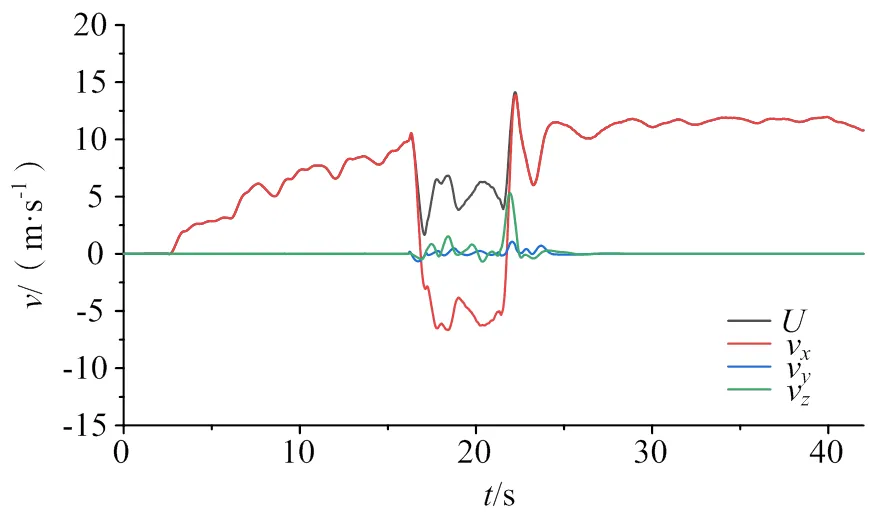
圖7 各滑流分量對比

2.2 同一縱向截面

圖8（a）（b）（c）分別繪制了距離隧道中軸線1.7 m、2.2 m和2.7 m不同高度監測點位置的列車風流速，圖8（d）繪制了距離地面2.5 m不同水平距離監測點處測得的風速，1時刻與2時刻分別為頭車鼻尖通過監測點與尾車鼻尖通過監測點時刻。

圖8 同一截面縱向滑流對比

從圖8可以看出，隧道內活塞風的最大值均出現在尾流處，并且隨著橫向距離的增加、尾流流速最大值降低。同時，隧道風速對橫向距離的敏感程度低于垂向距離，與文獻[17]中明線運行情況的結果不同，主要是因為露天環境沒有壁面限制，隧道內受隧道壁面的干預，致使隧道內氣體流動主要受活塞效應與摩擦效應的影響，而隧道內橫向相較于垂向受到更多限制，所以隧道內氣體流速對垂向距離更加敏感。當地鐵車輛通過時，隧道壁面與車體壁面之間形成渦流，導致靠近隧道壁面處氣體流動方向與地鐵車輛運行方向相反。

2.3 隧道內活塞風特性曲線

圖9繪制了列車中點處縱向截面流速云圖，可知：由于車底部分轉向架與車底設備的影響，底部區域氣流流速快且峰值幾乎不變；車頂及其以上部分，由于空間大且車頂設備較少，此處氣流流速受車體運動影響較小，所以隨著高度的增加峰值下降平緩；而車體中部由于靠近車體，受車體側壁的影響，隨著垂直高度的增加，氣體流速峰值迅速降低。車底與車頂部分為緩慢下降區域，中部為快速下降區域。

根據此平面距離中軸線2.2 m監測點氣體流速可擬合快速下降區的活塞風曲線，擬合公式見式（3），描述了距離中軸線2.2 m處隧道內氣體流速與高度的相互關系，可以看出，在列車中部附近氣體流速對于高度位置最敏感，此敏感性與隧道形狀、車體形狀等因素有關。

2.4 隧道內壓力波

為分析隧道內壓力波的作用，分析隧道入口監測點、隧道內監測點以及隧道出口監測點氣體流動情況，如圖10所示。其中N與T分別代表頭車鼻尖與尾車鼻尖位移，黃色直線代表與列車同向壓力波，實線為壓縮波，虛線為膨脹波，藍色直線代表與列車反向壓力波，實線為壓縮波，虛線為膨脹波。

圖9 沿垂向高度局部氣流流速變化

從圖10可以看出，由于車頭進入隧道時引起壓縮波效應，氣體流動速度在N到達之前就開始上升，1時刻頭車進入隧道，此時頭車經過隧道入口監測點，壓縮隧道內氣體從而產生壓縮波；2時刻尾車經過隧道入口監測點，產生膨脹波；3、4分別為頭車經過隧道內監測點與隧道出口檢測點時刻；5、6分別為尾車經過隧道內監測點與隧道出口檢測點時刻。此外，紅色直線標注了膨脹波與壓縮波傳播方向與列車同向的時刻，綠色直線標注了膨脹波與壓縮波傳播方向與列車反向的時刻，可以看出同向時，膨脹波會加速隧道局部流量，壓縮波會降低隧道內的局部氣體流速，而反向時膨脹波會降低隧道局部流量，而壓縮波會提升隧道局部氣體流速。

圖10 馬赫波對隧道內局部氣流的影響

2.5 人員安全退避距離

文獻[10]中確定人員安全距離的標準為列車尾部最大風速不超過14 m/s。繪制距離隧道中軸線2.7 m位置隧道風風速峰值變化，并進行二次曲線擬合，如圖11所示。

圖11 距離中軸線2.7 m活塞風風速峰值

從圖11可以看出，隧道內列車風風速峰值隨著列車運行位置增加，在距離入口750 m時達到最大值，隨后在距離入口750 m至隧道出口期間呈現下降趨勢。在接近隧道出口位置部分已經超過規定速度，因此在列車以100 km/h運行時，不建議人員在隧道內進行作業。

3 結論

采用非定常方法對某地鐵車通過隧道時產生的活塞風進行了CFD研究，結果總結如下：

（1）列車誘導的活塞風為三維流動，活塞風縱向分量和總流量變化基本一致，且縱向流量遠大于橫向流量和垂向流量，說明隧道內的氣體流動主要是一維縱向流。

（2）隧道內的壓力波對局部氣流有一定的影響。當壓力波的傳播方向與列車運行方向相同時，壓縮波的到來加速了局部氣體流速，而膨脹波則使其減小。當壓力波的傳播方向與列車運行方向相反時，壓縮波的到來降低了局部氣體流速，而膨脹波增強了局部氣體流速。

（3）活塞風縱向流量的最大峰值隨垂直高度的增加而減小，由于側向空間有限，流速最大峰值對側向距離的敏感性小于垂直高度，縱向流量的最大峰值隨側向距離的增大而減小。車輛底部區域氣流流速快且沿垂向變化緩慢，車頂部分及其以上部分氣流隨著高度的增加峰值下降平緩，而車體中部由于靠近車體，氣體流速迅速下降。

（4）當車速達到100 km/h時，隧道內活塞風流速最大值已經超過14 m/s，根據人員安全退避距離，未達到安全標準，因此在列車運行時，不建議隧道內人員作業。

[1]XIE Taizhong，LIU Tanghong，CHEN Zhengwei，et al. Numerical study on the slipstream and trackside pressure induced by trains with different longitudinal section lines[J]. Journal of Rail and Rapid Transit，2018，232（6）：1671-1685.

[2]CHEN Zhengwei，LIU Tanghong，YAN Chunguang，et al. Numerical simulation and comparison of the slipstreams of trains with different nose lengths under crosswind[J]. Journal of Wind Engineering & Industrial Aerodynamics，2019（190）：256-272.

[3]GUO Zijian，LIU Tanghong，CHEN Zhengwei，et al. Comparative numerical analysis of the slipstream caused by single and double unit trains[J]. Journal of Wind Engineering & Industrial Aerodynamics，2018（172）：395-408.

[4]WANG Shibo，Bell J R，Burton D，et al. The performance of different turbulence models (URANS, SAS and DES) for predicting high-speed train slipstream[J]. Journal of Wind Engineering & Industrial Aerodynamics，2017（165）：46-57.

[5]GUO Zijian，Liu Tanghong，Chen Zhengwei，et al a. Comparative numerical analysis of the slipstream caused by single and double unit trains[J]. Journal of Wind Engineering & Industrial Aerodynamics，2018（172）：395-408.

[6]CROSS D，HUGHES B，INGHAM D，et al. Enhancing the piston effect in underground railway tunnels[J]. Tunnel and Underground Space Technology，2017（61）：71-81.

[7]陳逸斐. 地鐵車輛端部底架疲勞壽命研究[J]. 機械，2021，48（1）：44-51.

[8]BS EN 14067-4：Requirements and Test Procedures for Aerodynamics on Open Track[S].

[9]LIAO S，et al. Aerodynamic Effects of High-Speed Trains on People and Property at Stations in the Northeast Corridor[R]. United States：Federal Railroad Administration，1999.

[10]田紅旗. 中國列車空氣動力學研究進展[J]. 交通運輸工程學報，2006（1）：1-9.

[11]劉堂紅，田紅旗，金學松. 隧道空氣動力學實車試驗研究[J].空氣動力學學報，2008（1）：42-46.

[12]梅元貴，王瑞麗，許建林，等. 高速列車進入隧道誘發初始壓縮波效應的數值模擬[J]. 計算力學學報，2016，33（1）：95-102.

[13]NIU Jinqiang，ZHOU Dan，LIU Feng，et al. Effect of train length on fluctuating aerodynamic pressure wave in tunnels and method for determining the amplitude of pressure wave on trains[J]. Tunnel and Underground Space Technology，2018（80）：277-289.

[14]WANG Yiwei，YANG Guowei，HUANG Chengguang，et al. Influence of tunnel length on the pressure wave generated by high-speed trains passing each other[J]. Science China Technological Sciences.，2012，55（1）：255-263.

[15]CHEN Xiaodong，LIU Tanghong. ZHOU Xisai，et al. Analysis of the aerodynamic effects of different nose lengths on two trains intersecting in a tunnel at 350 km/h[J]. Tunneling and Underground Space Technology，2017（66）：77-90.

[16]ZHANG Na，LU Zhaijun，ZHOU Dan. Influence of train speed and blockage ratio on the smoke characteristics in a subway tunnel[J]. Tunneling and Underground Space Technology，2018 （74）：33-40.

[17]HUANG Sha，HEMIDA Hassan，YANG Mingzhi. Numerical calculation of the slipstream generated by a CRH2 high-speed train[J]. Journal of Rail and Rapid Transit. 2016（230）：103-116.

Simulation Study on Piston wind Caused by 100 km/h Metro Vehicles Passing through Tunnels

PIAO Ronghuan，ZHANG Jiye，LI Tian

( State Key Laboratory of traction power, Southwest Jiaotong University, Chengdu 610031, China )

Metro vehicles passing through the tunnel induce the air flow, which will cause hidden danger to the ventilation in the tunnel, the operation of equipment and the safety of personnel. In order to eliminate these hidden dangers, this paper carries out a simulation study on the air flow caused by metro vehicles passing through the tunnel. The dynamic process is simulated by using the sliding mesh technology, and the airflow is monitored. The results show that the longitudinal component of piston wind in tunnel is consistent with the total flow, and the piston wind in tunnel is mainly longitudinal flow. The farther away from the car body or the ground, the smaller the maximum value of train air flow velocity. The piston wind at the vehicle bottom and roof decreases slowly along the vertical distance, but decreases rapidly in the middle of the car body. The maximum value of piston air flow velocity in the tunnel appears at 750 m away from the tunnel mouth.

metro vehicles；tunnel slipstream；pressure wave

U270.2

A

10.3969/j.issn.1006-0316.2021.11.006

1006－0316 (2021) 11－0041－08

2021－04－12

國家重點研發計劃（2016YFB1200403）；國家自然科學基金（51605397）

樸榮煥（1996－），男，內蒙古呼倫貝爾扎蘭屯市人，碩士研究生，主要研究方向為列車空氣動力學與耦合動力學，E-mail：piaoronghuan@126.com。*通訊作者：張繼業（1965－），男，四川夾江人，博士，教授，主要研究方向為高速列車空氣動力學，E-mail：jyzhang@swjtu.edu.cn。