基于NEMA編號和合流相位的跳相序感應控制策略

張帥鵬 柳祖鵬 何雅琴 姚昌宇

(武漢科技大學汽車與交通工程學院 武漢 430065)

0 引 言

感應控制是解決城市道路交叉口交通擁堵的有效方法之一.2003年，美國電氣制造商協會(national electrical manufacturers association，NEMA)面向典型的十字形信號控制交叉口，建立了具有8個機動車相位和4個行人相位，采用半環分析方法，定義起始相位和末尾相位兩種機動車相位屬性，討論可能存在的相位組合方案和相位切換方案，分析相位切換過程基本規律的NEMA雙環相位結構[1].

國內外學者基于NEMA雙環相位結構做了一系列的研究.黃謙[2]以NEMA相位為基礎，提出了一種通過排隊長度算法來確定周期和綠燈時間的交通配時優化模型.喬建明等[3]發現采用基于雙環8相位的交通信號控制方法,既避免相位沖突，又易形成搭接相位，操作起來標準且簡單.季策[4]通過引入了NEMA雙環相位結構，采用動態規劃方法實現相序的靈活優化，提出了一種單交叉口實時信號控制算法.曹政等[5]以NEMA雙環結構為基礎制定優先度規則,以此確定動態相位組合及相序排列.

國內外學者對交叉口感應控制的相關研究，有考慮各方向車流量的[6-7]，有考慮各相位排隊長度的[8-9]，有考慮車輛排隊長度和排隊時間的[10].韓平超[11]提出了相位需求度的概念，設計了相位需求度的計算方法和控制流程，但是相位需求度計算時只考慮了時間因素，無法合理地反映各個相位對綠燈信號的需求程度.柳祖鵬等[12]提出了綠燈需求度的概念，設計了綠燈需求度的計算方法和控制流程，但該控制流程是以相位結構固定為前提的，不能實現動態的相位組合.

對于合流相位的相關研究較少，郭英明等[13]利用VISSIM軟件對不同周期不同流量條件下的交叉口合流放行狀態進行仿真,結果表明：當出口車道數目與同時放行的左轉和直行車道數目之和相同或大于時,合流放行相位在理論上具備一定的可行性.肖文彬等[14]提出了合流流線相容的概念并用于交叉口信號控制的相關研究.

針對NEMA雙環相位結構的一些限制，例如北進口道的直行流量大，左轉流量小，但南進口道的直行流量小，左轉流量大，這時NEMA相位結構就無法實現調節.文中引用綠燈需求度的概念和計算方法，提出一種基于NEME編號和合流相位的跳相序感應控制策略，實現相位的動態組合，以解決城市道路交叉口交通擁堵問題.

1 NEMA雙環相位車流編號及其規律

NEMA雙環相位結構由8股機動車相位組成，見圖1.車流1、3、5、7為左轉車流，車流2、4、6、8為直右車流，NEMA雙環相位結構見圖2.同時，在將編號為9、10、11、12、13的虛擬車流分別對應編號為1、2、3、4、5的實際車流后，可以發現規律：設置編號為i的車流，當i為奇數時，與編號為i+3，i+4，i+5的車流分別構成合流、交叉、分流三種相位效果組合；反之，當i為偶數時，與編號為i+3，i+4，i+5的車流分別構成分流、交叉、合流三種相位效果組合.如編號為4的車流，4為偶數，與編號為7(4+3)的車流為分流，與編號為8(4+4)的車流為交叉，與編號為1(4+5)的車流為合流，見表1.

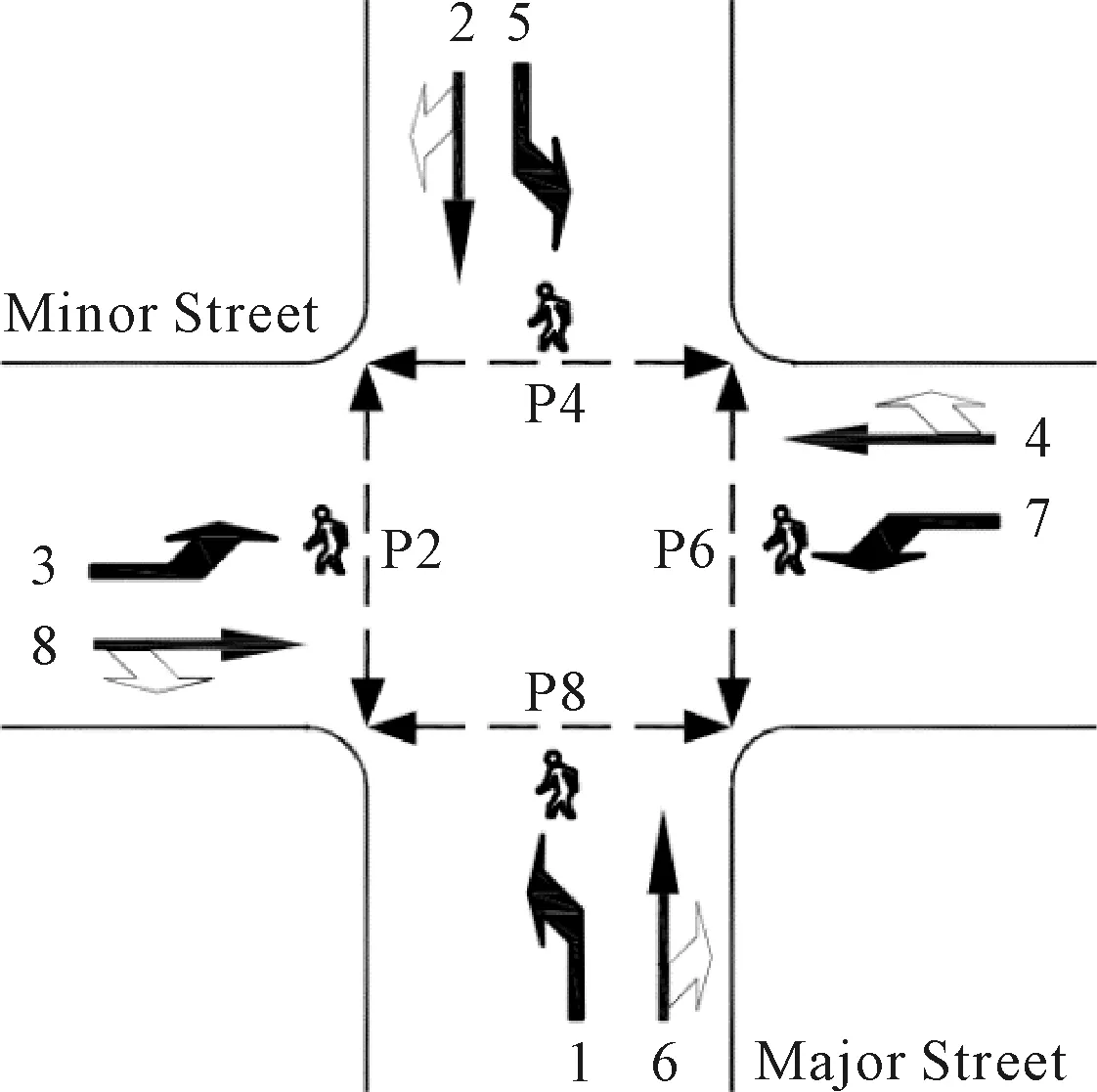
圖1 NEMA機動車相位編號圖

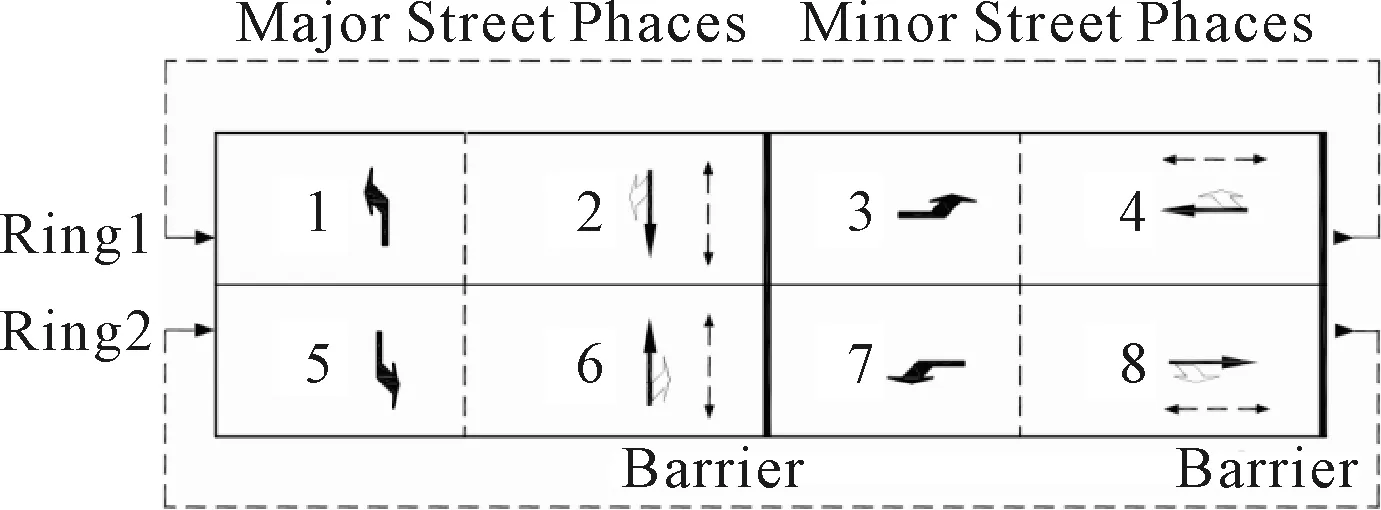
圖2 NEMA雙環相位結構圖

表1 NEMA機動車相位組合規律表

在考慮合流的前提下，8股車流的全部組合見表2.在考慮合流的前提下，8股車流的全部組合共有3×4=12種，其中(1,4)，(3,6)，(5,8)，(7,2)為合流.

2 合流相位

合流相位是指在同一出口道匯合的左轉和直行車流同時放行的綠燈相位.基于已有研究表明：當出口車道數目與同時放行的左轉和直行車道數目之和相同或大于時,合流放行相位在理論上具備一定的可行性.在本研究中，交叉口背景符合車道平衡條件，車輛在在交叉口內左轉或直行時嚴格按照規定車道行駛且不會變道.根據NEMA相位的車流編號，合流相位有四種情況：(1，4)，(3，6)，(5，8)，(7，2)為合流相位.以合流相位(1，4)為例，示意圖見圖3.

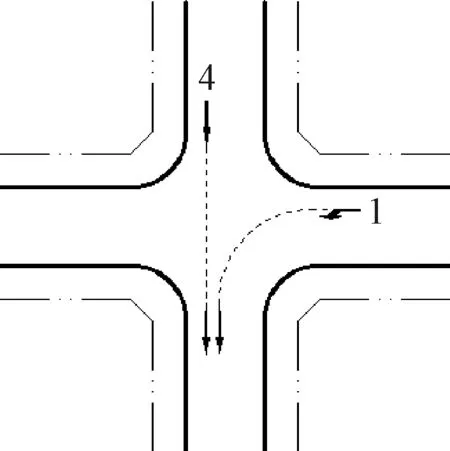
圖3 (1，4)合流相位示意圖

3 綠燈需求度

綠燈需求度(demand degree of green, DDG)是指不同相位在周期中的不同時間對綠燈信號的需求程度.處于紅燈相位下的車流的綠燈需求度與等待時間和排隊車輛數有關.為了統計紅燈相位下的排隊車輛數，在緊靠停車線的下游(停車線與人行橫道之間)布設“檢出檢測器”，在進口道上游大于最大排隊長度的位置布置“檢入檢測器”，不間斷統計檢入、檢出檢測器上的車輛到達脈沖，檢入脈沖時排隊數增加，檢出脈沖時排隊數減少，由此可統計得到各個相位在不同時刻的排隊車輛數.檢測器位置見圖4.

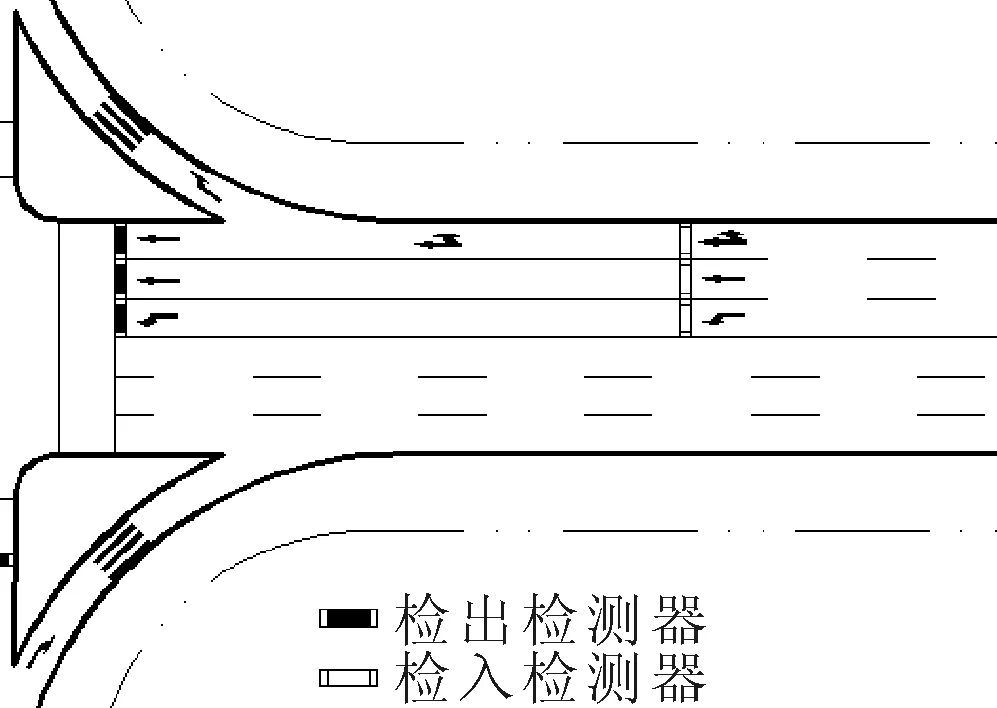
圖4 檢測器位置示意圖

紅燈開始時，累加該相位下每1s時間內的等待車輛數，即累加該相位下每一輛車已經等待的時間，計算公式為

(1)

式中：DDG為綠燈需求度，veh·s；R為當前紅燈時間；t為時間變量，從1增加到R；veh(t)為t-1～t這1 s內該相位下的排隊車輛數.

根據車輛檢測器的檢測信息，經統計可以得到該相位下每1 s的車輛排隊數veh(t)，由此計算得到的綠燈需求度可以全面的反映紅燈相位下的等待時間和排隊情況.從而使得排隊車輛較多且等待時間較長的車流所在的相位獲得優先通行權.

4 感應控制策略

4.1 相位切換

相位切換分為三種情況，以相位最小綠燈時間和相位最大綠燈時間為分界點，表示為：

1) 任一相位綠燈起始，在感應信號控制內設置最小綠燈時間，在最小綠燈時間結束之前，不進行相位切換.

2) 到最小綠燈時間結束時，如果在一個預先設置的時間間隔內沒有后續車輛到達，切換相位；如果有車輛到達，則延長綠燈時間，只要不斷有車到達，綠燈時間可繼續延長，直到預設的最長綠燈時間.

3) 當相位綠燈時間大于等于最大綠燈時間時，切換相位.

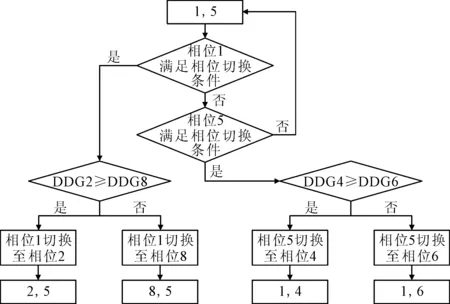
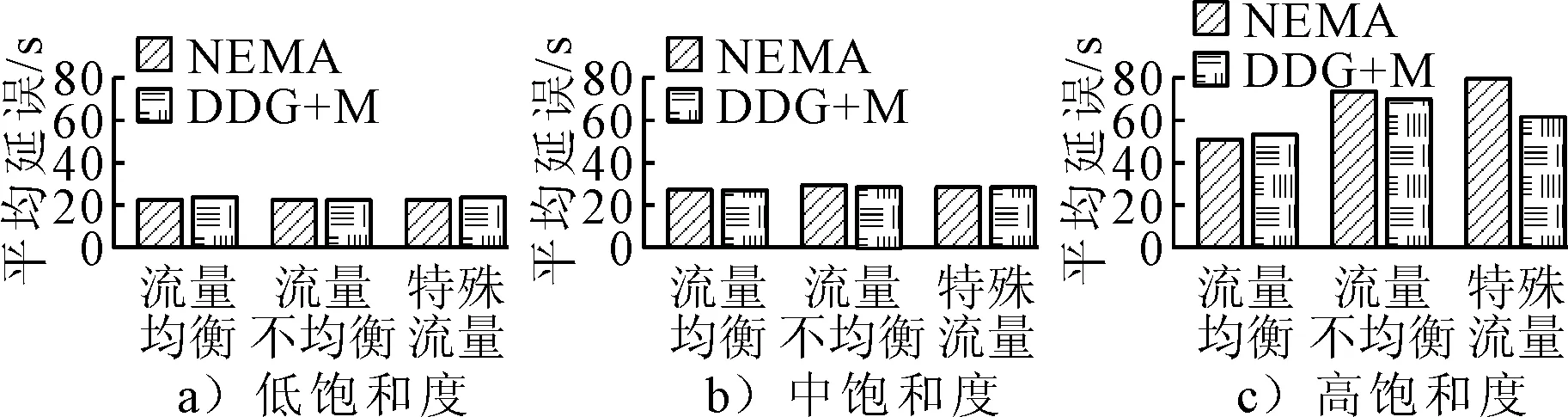
用數學表達式表示為以下三個階段：①0≤t相

4.2 相位選擇

采用全感應控制，以NEMA雙環結構中定義的8個機動車相位為基礎，在8個機動車相位對應進口道上都設置檢測器，并根據車輛檢測器的檢測信息，計算得到對應相位的綠燈需求度.在每一次選擇下一個切換相位時，選擇此時不沖突且綠燈需求度最大的相位為下一個變換相位.

通過相關研究和觀察可知，在NEMA相位結構中，交叉口至多只能使2股機動車相位的車流同時通過，通常情況下，為了使交叉口時空資源得到充分利用，交叉口信號控制都是以2股機動車相位為基礎，這樣既充分利用了資源，又避免了沖突.處于綠燈狀態下的2股機動車相位，當其中1股機動車相位滿足相位切換條件時，選擇該機動車相位對應的不沖突且綠燈需求度最大max(DDGi)的相位進行切換.以相位1和5為例，示意流程圖見圖5.

圖5 相位切換示意流程圖

5 仿真測試與分析

5.1 仿真測試環境

以武漢市團結大道-園林路交叉口為例，該交叉口4個進口道均為3車道，其中直行與右轉共用2車道，左轉專用1車道.見圖6.

圖6 交叉口布局示意圖

仿真運行時，共運行4 000 s，前400 s作為路網車流初始化階段.設置多個仿真種子運行仿真試驗，試驗結束后輸出所有車輛的平均延誤作為評價指標.

5.2 仿真場景

根據車流流量差異設置“流量均衡”“流量不均衡”和“特殊流量”三種場景.①流量均衡場景下，主、次干路流量比約為3∶2，左、直、右流量之比為3∶6∶1，上下兩環的流量之和基本相等，車流1+車流2約等于車流5+車流6，車流3+4約等于車流7+8.②流量不均衡場景下，主、次干路流量比約為3∶2，上環流量之和大于下環流量之和，車流1+2大于車流5+6，車流3+4大于車流7+8.③特殊流量場景下，主、次干路流量比約為3∶2，上下環流量之和基本相等，車流1+2大于車流5+6，車流7+8大于車流3+4.以上3種場景下，再分別設置低、中、高三種不同的飽和度，交叉口的流量分別為2 000，4 000和5 600輛/h.

設置兩種感應控制方案：①NEMA雙環結構感應控制，用“NEMA”表示；②基于綠燈需求度的跳相序感應控制，用“DDG+M”表示.

5.3 仿真結果及分析

匯總多次仿真實驗的平均延誤評價數據，得到3×3=9種不同條件下的交叉口平均延誤對比圖，見圖7.

圖7 不同場景下，不同飽和度的延誤對比

由圖7可知，流量均衡場景下，相較于NEMA控制策略，DDG+M控制策略的延誤整體較大，其中在高飽和度情況下，相較于NEMA控制策略，DDG+M控制策略下的平均延誤增加了2.26 s，增加了4.5%.流量不均衡場景下，相較于NEMA控制策略，DDG+M控制策略的延誤整體較小，其中在高飽和度情況下，相較于NEMA控制策略，DDG+M控制策略下的平均延誤減少了4.02 s，降低了5.5%.特殊流量場景下，相較于NEMA控制策略，DDG+M控制策略的延誤整體較小，其中在高飽和度情況下，相較于NEMA控制策略，DDG+M控制策略下的平均延誤減少了17.68 s，降低了22.4%.由此可見，相較于NEMA控制策略，DDG+M控制策略更適用于流量不均衡和特殊流量場景的交叉口.

不同飽和度條件下，不同場景的延誤對比圖，見圖8.

圖8 不同飽和度條件下，不同場景的延誤對比

由圖8可知，低飽和度條件下，三種場景下的兩種控制策略的延誤相差不多，原因是交通流量過小，各車流在最小綠燈時間內均完全駛入交叉口，無法凸顯控制策略調節效果.中飽和度條件下，三種場景下的兩種控制策略的延誤相差不多，都在1 s以內，原因是交通流量適中，兩種控制策略的調節效果差距不明顯.高飽和度條件下，兩種控制策略調節效果開始凸顯，在高飽和度流量均衡場景下，相較于NEMA控制策略，DDG+M控制策略下的平均延誤增加了2.26 s，增加了4.5%.在高飽和度流量不均衡場景下，相較于NEMA控制策略，DDG+M控制策略下的平均延誤減少了4.02 s，降低了5.5%；在高飽和度特殊流量場景下，相較于NEMA控制策略，DDG+M控制策略下的平均延誤減少了17.68 s，降低了22.4%.

匯總不同流量場景和不同飽和度條件下，NEMA和DDG+M控制策略的延誤對比，見圖9.由圖9可知，在流量均衡場景下，NEMA控制策略較優，但兩者交叉口平均延誤相差不大；在流量不均衡和特殊流量下，DDG+M控制策略較優，特別是在流量不均衡和特殊流量場景的高飽和度交叉口，DDG+M控制策略都具有明顯的優勢.

圖9 各種組成場景下的延誤對比

6 結 束 語

基于NEMA雙環相位結構的相關研究，充分證明了NEMA相位的合理性和在交叉口控制中的優勢，其對于相位的定義以及獨有的具有規律的相位編號方式方便了相關研究.紅燈相位下的綠燈需求度的計算方法充分考慮了車輛的排隊和等待時間，合理地反映出了各個紅燈相位對于綠燈信號的需求程度.在滿足當出口車道數目與同時放行的左轉和直行車道數目之和相同或大于時的前提下，合流相位的存在將實現交叉口相位的動態組合.

仿真測試和結果表明，在流量不均衡和特殊流量的交叉口，基于綠燈需求度的感應控制策略比NEMA雙環相位結構更有效，且其控制效果隨著流量的增加表現得越來越明顯.

后續擬在車輛以車隊行駛方式到達的條件下，進一步對該控制策略進行驗證和改進.單點信號控制是干線協調控制的基礎，后續研究可在單點控制的基礎上擴展到干線甚至區域層面，并在實踐中進行測試和驗證.