雙模量梁動力響應的時域GD法求解
黃春林 彭建設
(成都大學機械工程學院 成都 610106)
0 引 言
除了金屬材料,工程材料的實際運用中的玻璃鋼、塑料、混凝土、橡膠、粉末冶金材料、聚合材料及復合材料等等都具有一定的拉壓彈性模量不等的性質.由于雙模量材料的大量使用,學者們也對其展開了深入的研究。潘勤學等[1]探討了不同模量理論廣義彈性定律的意義并進行了討論梳理.對于雙模量梁的振動問題,劉相斌等[2]在平截面假定下提出了雙模量梁振動過程中中性軸會發生跳變,并分析了雙模量彎曲梁的固有頻率和主振型.王銘慧等[3-4]在平截面假設下對拉壓彈性模量不等材料簡支梁的線性振動和非線性振動頻率問題進行了研究.楊洋等[5]推導并分析不同模量鐵木辛柯梁的自由振動頻率特性.吳曉等[6]研究了考慮剪切效應及阻尼時雙模量梁的自由振動固有頻率問題.但對于雙模量梁的受迫振動的時程響應鮮有研究。文中基于雙模量理論,運用時域GD法研究均布交變載荷和均布突加載荷作用下簡支雙模量梁受迫振動的時程響應,討論了拉壓彈性模量不等對受迫振動的影響.
1 GD法簡介
GD法(general differential method)是在利用泰勒展開的基礎上來使用全域的節點函數值來表示某個基點處的導數值.將某連續函數在基點處做泰勒展開,用全域內節點函數值的加權和來表示基點的導數,從而將微分方程轉化為可解的代數方程組,通過求解代數方程組來得到微分方程的解.在域內沿x方向取N個等間距為h節點xi(i=1,2,…,N),設f=f(x)是彈性體內某一連續函數,該函數只隨x坐標變化而變化,以起點為基點,其余各點可展開為泰勒級數,則以第i個節點為基點,則任意第n(n≠i)點函數值可以用h表示為
(1)
稱fi(i=2,3,…,N-1)為內節點,f1,fN為外邊界節點.將各節點(N=1,2,…,i-1,i+1,…,N)整理為如下矩陣.
(2)
式中:

(3)
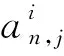
該表達式改寫為
Aif=W
(4)
式中:Ai為第i個節點展開的系數矩陣;f為導數矩陣;W為展開點與基點的差值的矩陣.可得到導數矩陣:
f=MiW
(5)
式中:Mi為Ai通過Gauss-Jordan消元法得到的逆矩陣,詳細推導過程參見文獻[7],由之得到第i個節點的1,2,…,N-1階導數值.其中第i個節點的k階導數可表示為
(6)
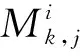
域內不同節點的同階導數系數列陣可按不同基點展開分別求逆,然后將不同節點的同階導數整理到一個矩陣C,詳細內容參見文獻[7].
由之可得任意i節點的k階導數為
(7)
權系數矩陣C的表達式為
(8)
2 時域GD法解雙模量梁的受迫振動問題
2.1 雙模量梁的幾何關系與本構方程
長度為L、寬為b、高為h,拉伸和壓縮彈性模量分別為Et和Ec的矩形截面梁.考慮在線彈性小變形范圍內,定義梁的中面層位移為(u,w),則梁的任意縱向截面層距離中面層為y的點的位移為(u′,w′),兩者間的幾何關系為
(9)
(10)
式中:ρ為梁彎曲變形后中性層的曲率半徑.
于是在線彈性范圍內,定義雙模量梁中性層到幾何中面的距離為y0,有
(11)
由材料的本構關系可得
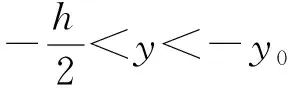
(12)
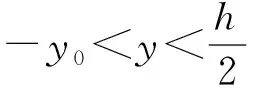
(13)
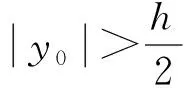

(14)
(15)
將式(12)~(13)代入式(14)~(15)分別可得
(16)
(17)
由式(15)可知,振動過程中即使中性軸位置發生跳變,彎矩M的表達式不變.
結合式(17)可得雙模量梁的抗彎剛度為
(18)
設Ec/Et=λ,式(18)可改寫為
(19)
當拉壓彈性模量相等即λ=1時,式(19)可退化為經典的等模量梁的抗彎剛度.
2.2 雙模量梁的振動控制微分方程
設雙模量材料的密度為ρ1,則根據達朗貝爾原理,可以得到雙模量梁的橫向自由振動的控制微分方程:
(19)
式中:w為橫向位移;A為橫截面積。為方便求解,改寫為按位移表達形式后,可得雙模量梁的受迫振動控制微分方程.
(20)
式中:(EI)*為梁的抗彎剛度;x為梁沿軸向的自變量;t為時間;w(x,t)為梁的振動小撓度;y0為中性層相對于中面層的距離;ρ1為材料密度;q(x,t)為隨時間變化的載荷.
2.3 雙模量梁振動微分方程的時域GD法求解
針對均布載荷下梁結構的受迫振動響應問題,運用時域GD法求解此類問題,將該問題的控制方程和邊界條件在時間域和空間域都使用GD法離散,得到全域內關于該振動問題的一次線性方程組,在權系數矩陣和廣義載荷列陣融入邊界條件,使線性方程組可解。通過求解融入邊界條件和初始條件的可解一次線性方程組,可得全域內梁振動的位移響應場。
控制方程量綱一的量化,令X=x/L,X∈[0,1],τ=t/T,τ∈[0,1]可得量綱一的量控制方程.
(21)
在空間域取Nx個節點,在時間域內取Nτ個節點并使用GD法離散處理,則有:
(22)
(23)
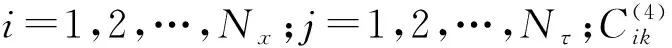
(24)
式中:i=1,2,…,Nx;j=1,2,…,Nτ.
由之可得,在全域內有Nx×Nτ個GD線性方程組,將式(24)改寫成矩陣形式,
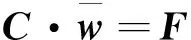
(25)
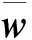
為求解GD線性方程組,需確定定解條件.梁在任意時間節點τj(j=1,2,…,Nτ)都有4個邊界條件,在全域內有4Nτ個邊界條件,以簡支梁為例,其邊界條件為
即
(26)
此外,梁在X空間域任意節點Xi(i=1,2,…,Nx)處有兩個初始條件,在全域內有2Nx個初始條件,簡支梁初始條件為
即
(27)
3 算例分析
例1兩端簡支的梁,長L=50 cm,橫截面寬1 cm、高2 cm,質量密度ρ=0.008 kg·cm-3,彈性模量E=15 000 000 N·cm-2,上作用一q=10sin(500t) N·cm-1均布交變載荷.初位移和初速度均為零,求梁中點的位移響應.
例2兩端簡支雙模量梁,其幾何參數同例1,拉伸彈性模量Et=15 000 000 N·cm-2,質量密度ρ=0.008 kg·cm-3,在梁上作用一q=10sin(500t) N·cm-1均布交變載荷,初始位移和初始速度均為零,求當壓縮與拉伸彈性模量之比Ec/Et=λ分別為0.7,1,2,4時梁中點x=25 cm處的位移響應.
例3兩端簡支雙模量梁,其幾何參數同例1,拉伸彈性模量Et=15 000 000 N·cm-2,質量密度ρ=0.008 kg·cm-3,在梁上作用一q=1 N·cm-1突加均布載荷,初始位移和初始速度均為零,求當壓縮與拉伸彈性模量之比Ec/Et=λ分別為0.7,1,2,4時雙模量梁中點x=25 cm處的位移響應.
三個算例數值結果如下:為說明方法的準確性,針對算例1相同節點用精確解,Newmark-β解和本文的時域GD解列出具體數值見表1,算例1~3對應的圖像見圖1.

表1 算例1精確解與兩種數值解
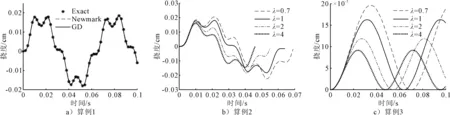
圖1 三種方法對比結果
算例1為經典的單模量情況,使用2.3的方法解決問題時,將雙模量梁的抗彎剛度(EI)*中λ取為1即可.
求解算例1,當使用時域GD法求解時,在空間域取13個節點,時間域取101個節點,時間步長為0.001 s;使用Newmark-β法求解時,在空間域取13個節點,取時間步長為0.001 s,使Newmark-β法與時域GD法的時間步長相等.由表1和圖1a)可知,在相同的時間步長的情況下,時域GD法的解與精確解的誤差小于Newmark-β法與精確解的誤差.說明時域GD法解決該問題是可行的,所得結果是可信的.
由圖1b)可知,λ=1時的結果與經典單模量理論E=15 000 000 N·cm-2時等效;從結果可以看出當λ=0.7時其受迫振動正向幅值相對于λ=1時增大13.5%,負向振動幅值增大22.9%,響應周期增大9.3%;當λ=2時,其受迫振動幅值相對于λ=1時減小但不明顯,而響應周期減小14%;當λ=4時,其受迫振動幅值相對于λ=1時減小,其中正向幅值變化不明顯,但負向幅值減小21.3%,響應周期減小28%.
由圖1c)可知,λ=1時的結果等效于經典單模量理論時彈性模量梁E=15 000 000 N·cm-2的位移響應結果,與λ=0.7時的結果比較,λ=1時振動幅值減小17%,響應周期也減小8.6%;當λ=2時的結果與λ=1時相比,其受迫振動幅值減小27%,響應周期減小15.6%;當λ=4時的結果與λ=1時相比,其受迫振動幅值減小44.7%,響應周期減小25%;.這是由于彈性模量比λ的增大,使得使梁的抗彎剛度增大,最終導致梁的振幅和響應周期減小.
4 結 論
1) 相較于Newmark-β法,時域GD法在時間步長與之相等時,時域GD法與精確解的誤差更小.
2) 隨著比值λ的增大,中性軸位置偏離幾何中面的距離越大,使梁的抗彎剛度得到提升,導致雙模量簡支梁受迫振動的振幅和響應周期都會相應的減小.而比值λ越大,振幅與響應周期越小.
3) 隨對于雙模量梁的動力響應問題,若簡化為單模量問題計算可能與實際問題產生較大誤差,彈性模量比值λ越大,誤差越大.

