超高性能混凝土柱的抗震性能分析

方 志， 方文昌， 胡 銳， 董長征

(1.湖南大學 土木工程學院， 湖南 長沙 410082； 2.湖北省交通投資集團有限公司， 湖北 武漢 430050)

超高性能混凝土(Ultra-High Performance Concrete，UHPC)是20世紀90年代國外研發的一種具有超高強度和優異耐久性的新型水泥基復合材料[1]。UHPC的抗壓比強度(抗壓強度/材料容重)約為普通混凝土的4倍，由此可顯著減小配筋混凝土構件的截面尺寸，從而減輕結構自重、增加結構的變形能力、減小結構的地震作用[2]；此外，UHPC的高韌性和高延性可使結構吸收更多的地震能量，從而增強結構的抗震能力[3]。因此，與普通混凝土結構相比，采用UHPC有望形成抗震性能更為優越的配筋混凝土結構。

ZOHREVAND P[4]等對柱腳兩倍塑性鉸長度范圍內采用UHPC代替普通混凝土的混合橋墩進行了擬靜力試驗試驗，結果表明：UHPC可以顯著提高試件的耗能能力。PALACIOS[5]等對塑性鉸區采用UHPC的柱進行了擬靜力試驗，結果表明：UHPC柱具有良好的抗震性能，柱的配箍率可相應降低。MARCHAND P[6]等對無箍筋或配少量箍筋UHPC柱的抗震性能進行了試驗研究，結果表明：箍筋的作用較小，尤其是軸壓比較大時更是如此。

趙冠遠[7]等對4根UHPC柱進行了擬靜力試驗，結果表明：UHPC柱抗震性能良好，箍筋對UHPC柱約束作用不明顯。王誠[8]等對3根UHPC箱型墩進行了擬靜力試驗，結果表明：UHPC箱型墩抗震性能良好，水平荷載方向角是影響抗震性能的一個重要因素。鞠彥忠[9]等對18根UHPC柱進行了擬靜力試驗，結果表明：軸壓比越大，試件承載力越高，延性越差；配筋率、配箍率越大，試件延性和耗能能力均越好；增加鋼纖維摻量，可提高柱的延性和耗能能力。

現有研究均表明UHPC柱抗震性能良好，但相關研究仍較有限。基于此，本文采用開源有限元軟件OpenSees(Open System for Earthquake Engineering Simulation)建立了UHPC柱全過程受力的分析模型，并對UHPC柱進行了擬靜力試驗，獲得了柱的全過程受力形態，用以驗證分析模型的適用性；基于被試驗結果驗證的有限元模型，對試件受力全過程進行了數值模擬，分析了不同參數對UHPC柱抗震性能的影響。

1 試驗概況

1.1 試件設計

試件尺寸和配筋如圖1所示。柱總高為3 600 mm，中部凈高為2 800 mm，截面為200 mm×300 mm矩形截面，采用強度等級為150 MPa的UHPC澆筑，UHPC為商品預混料，鋼纖維體積含量2%、長度13 mm、直徑0.2 mm、抗拉強度≥2 000 MPa；用于柱頂端加載和底部固定的柱帽和底座高均為400 mm，采用C50混凝土澆注；柱縱向采用6根直徑16 mm的HRB500鋼筋，截面上對稱布置，箍筋采用直徑8 mm、間距200 mm的HRB400鋼筋。試件制作時先澆筑UHPC柱體并采用蒸汽養護，澆筑完成靜置48 h后，再使用90 ℃蒸汽養護48 h。UHPC柱養護完成后，再澆筑兩端的普通混凝土柱帽和底座。普通混凝土澆注前，將UHPC柱內預留縱筋深入其內足夠錨固長度并將預制UHPC柱體伸入底座和柱帽各3 cm，以保證預制件與后澆部分的整體性。實測試件所采用材料性能的特征值分別如表1和表2所示，表1中C50抗拉強度根據文獻[10]計算，其余均為實測值。

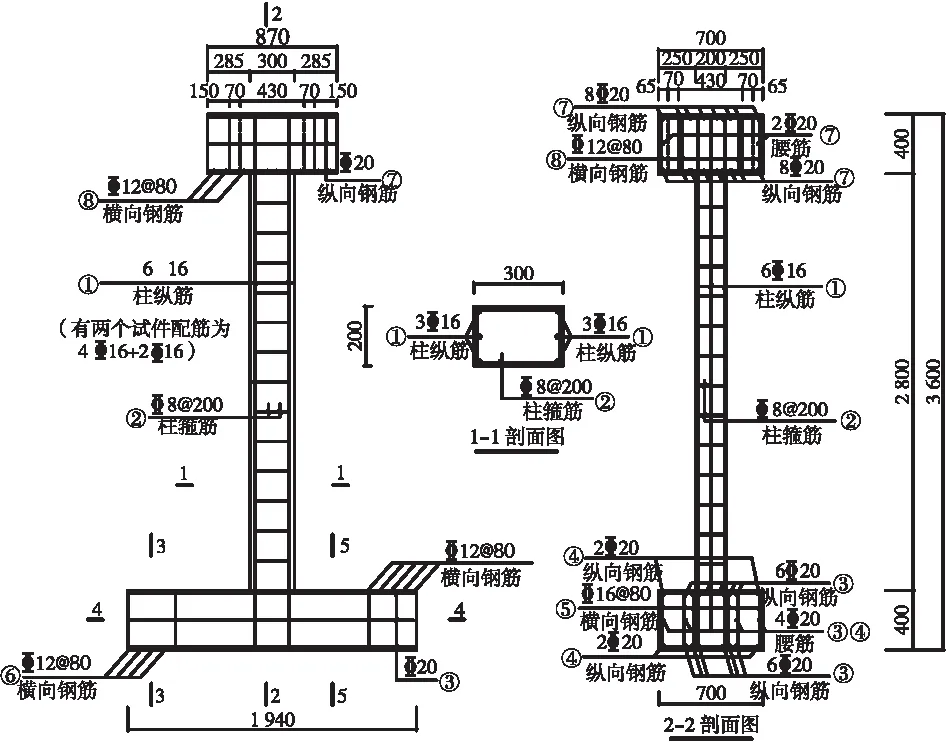
圖1 試件尺寸及配筋(單位： mm)Figure 1 Diemnsion and reinforcement of specimens(Unit: mm)

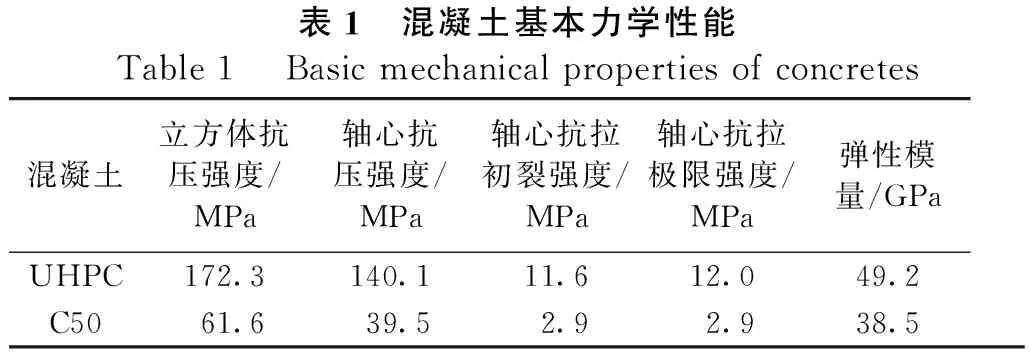
表1 混凝土基本力學性能Table 1 Basic mechanical properties of concretes混凝土立方體抗壓強度/MPa軸心抗壓強度/MPa軸心抗拉初裂強度/MPa軸心抗拉極限強度/MPa彈性模量/GPaUHPC172.3140.111.612.049.2C5061.639.52.92.938.5

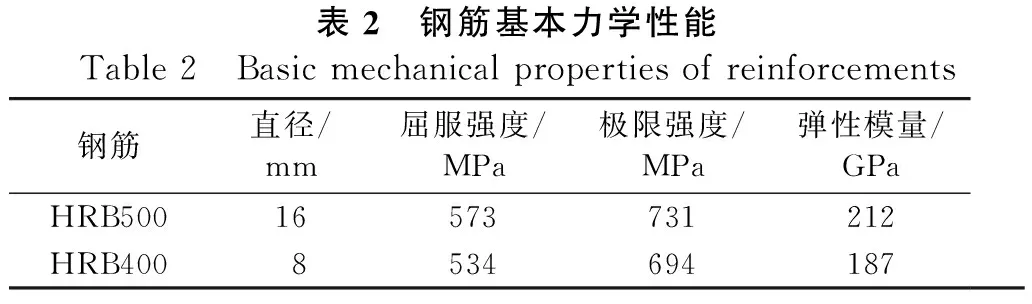
表2 鋼筋基本力學性能Table 2 Basic mechanical properties of reinforcements鋼筋直徑/mm屈服強度/MPa極限強度/MPa彈性模量/GPaHRB50016573731212HRB4008534694187

1.2 加載裝置和方案

試件采用多功能結構試驗裝置(Multi-Usage Structural Testing System，MUST)進行加載，加載裝置如圖2所示。軸壓力通過4個豎向作動器施加，水平荷載通過2個水平作動器施加，先加豎直荷載至額定值，再施加水平荷載至柱破壞。柱試驗軸壓比為0.1，相應的軸壓力840 kN。

圖2 加載裝置Figure 2 Loading set-up

參照相關試驗規程[11]及文獻[12]，對試件采用基于層間位移角控制的位移控制加載，加載制度見表3。每級荷載循環3次，直至試件破壞或荷載降低至極限承載能力的85%以下。

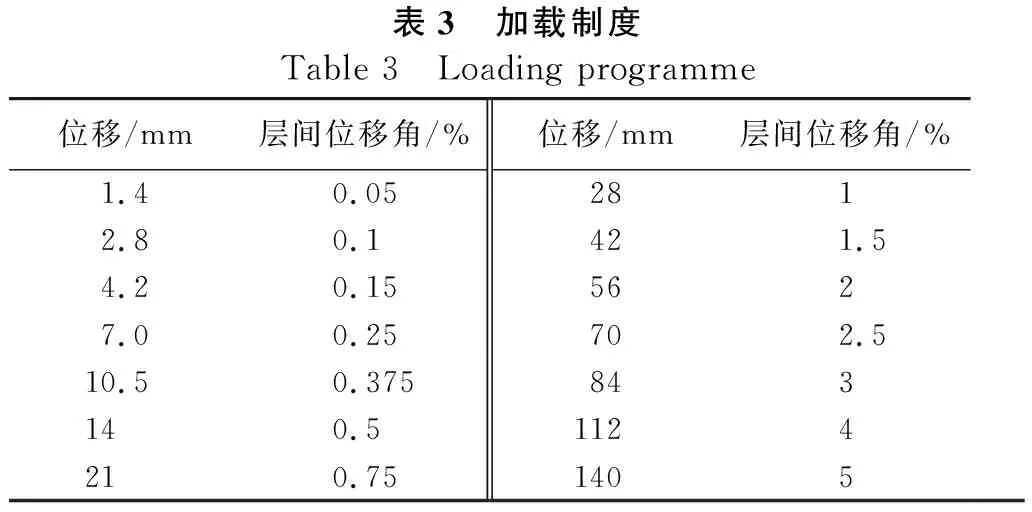
表3 加載制度Table 3 Loading programme位移/mm層間位移角/%位移/mm層間位移角/%1.40.052812.80.1421.54.20.155627.00.25702.510.50.375843140.51124210.751405

1.3 試驗現象

位移小于6.3 mm時，水平荷載為79.6 kN，試件未出現裂縫，荷載-位移曲線呈線性，無殘余變形；位移達到7.8 mm時，水平荷載為94.5 kN，試驗柱左上角出現初始裂縫，寬度為0.01 mm；位移達到20.0 mm時，水平荷載達到峰值127.3 kN，試驗柱四個角均有裂縫產生，最大裂縫寬度為0.07 mm；此后，試件水平荷載開始下降；位移達到55.7 mm時，水平荷載下降至124.1 kN，柱頂裂縫繼續發展，正向裂縫與負向裂縫交叉，最大裂縫寬度為0.18 mm，并且在試驗柱的拐角處觀察到局部混凝土壓碎；位移達到105.5 mm時，最大裂縫寬度為0.23 mm，水平荷載下降至103.2 kN，為極限承載能力的83%，判定試件破壞，終止加載并卸載。試件破壞形態與裂縫分布如圖3所示。

圖3 試件破壞形態與裂縫分布Figrue 3 Failure modes and crack distribution of specimens

2 分析模型建立

2.1 截面與單元類型選取

OpenSees中截面恢復力模型有彈性模型、理想彈塑性模型、雙折線強化模型等常規模型和比較精細的纖維模型。纖維模型是將截面劃分為一定數量的離散小纖維，并可在各纖維內定義不同的材料本構關系，可較好地反映出截面的材料特性和鋼筋分布特點，因此本文選用纖維截面模型。

OpenSees中非線性梁柱單元(Nonlinear Beam-Column Elements)分為基于力的梁柱單元和基于位移的梁柱單元，前者計算精度高但不易收斂，后者易于收斂但精度比前者稍低，不過可以通過增加單元數量來提高計算精度，因此本文選用基于位移的梁柱單元。

2.2 材料本構關系

UHPC采用OpenSees中基于Thorenfeldt曲線的Concrete06 Material本構，相關參數取UHPC材料的測試值；卸載方式為分段線性卸載，卸載與再加載路徑取為不同，以便更準確地模擬混凝土的滯回特性，Concrete06的應力 — 應變關系滯回本構如圖4所示[13]。

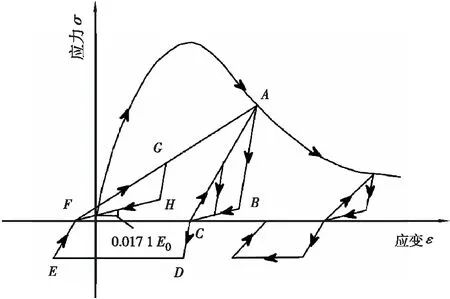
圖4 UHPC的滯回本構Figure 4 Constitutive relationship of UHPC

UHPC單軸受壓本構方程為式(1)：

(1)

式中：σc為壓應力；fc為軸心抗壓強度；εc0為峰值壓應變；n為受壓應變-應變曲線形狀系數，取n=2；k為峰值壓應變后應力 — 應變曲線形狀系數，取k=1.33。

UHPC單軸受拉本構方程為式(2)：

(2)

式中：σt為拉應力，E0為彈性模量；fte為軸心抗拉初裂強度；εte為初裂應變，且εte=fte/E0；εtu為極限拉應變；b為受拉應變-應變曲線形狀系數，取b=0.05。依據文獻[14]的研究結果，取：

fte=ft0(1+αtλf)

(3)

(4)

式中：ft0為基體抗拉強度，根據文獻[15]ft0=0.047fcu，k；鋼纖維影響系數t=0.32；鋼纖維特征參數λf=ρflf/df，ρf、lf、df分別為鋼纖維的體積摻量、長度和直徑。

根據材性試驗和文獻[15]，定義UHPC本構時的參數取值如下：fc為140.1 MPa，εc0為3.20×10-3，E0為49.2 GPa，fte為11.6 MPa，εtu為3.88×10-3。

鋼筋采用基于Giuffre-Menegotto-Pinto模型的Steel02 Material本構，其采用應變的顯函數形式，計算效率高，同時也考慮了等向應變硬化和包辛格效應的影響，鋼筋的應力-應變關系本構模型如圖5和式(5)所示。

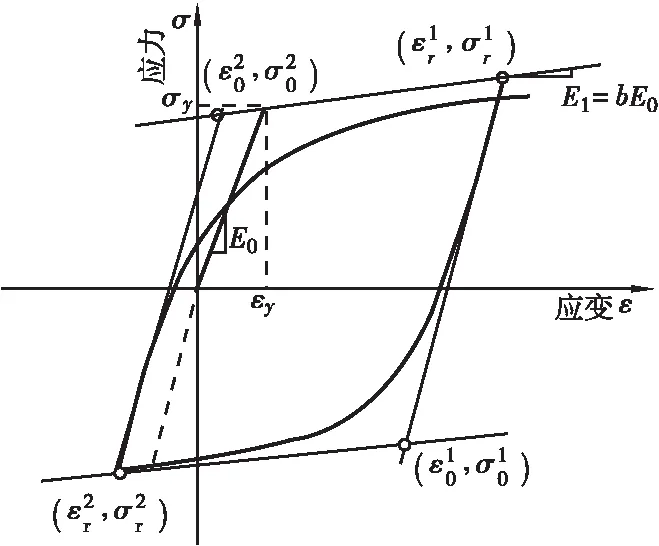
圖5 鋼筋本構Figure 5 Constitutive model of reinforcement

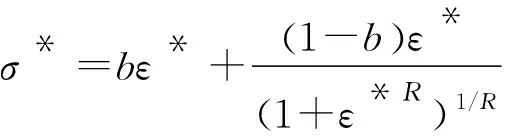
(5)

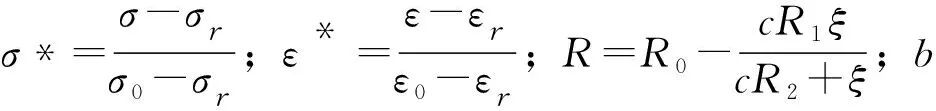
根據材性試驗和OpenSees用戶手冊，定義鋼筋本構時的參數取值如下：鋼筋為HRB500，fy為573 MPa，E為212 GPa，b為0.01，R0為18.5，cR1為0.925，cR2為0.15。

2.3 結果對比

圖6為試件受力變形性能模擬值與試驗值的比較，峰值點處極限承載能力及相應水平位移實測值分別為127.3 kN和20.04 mm，相應的預測值分別為127.7 kN和19.60 mm，受力全過程的預測結果與試驗結果吻合較好，驗證了所建立分析模型的適用性。

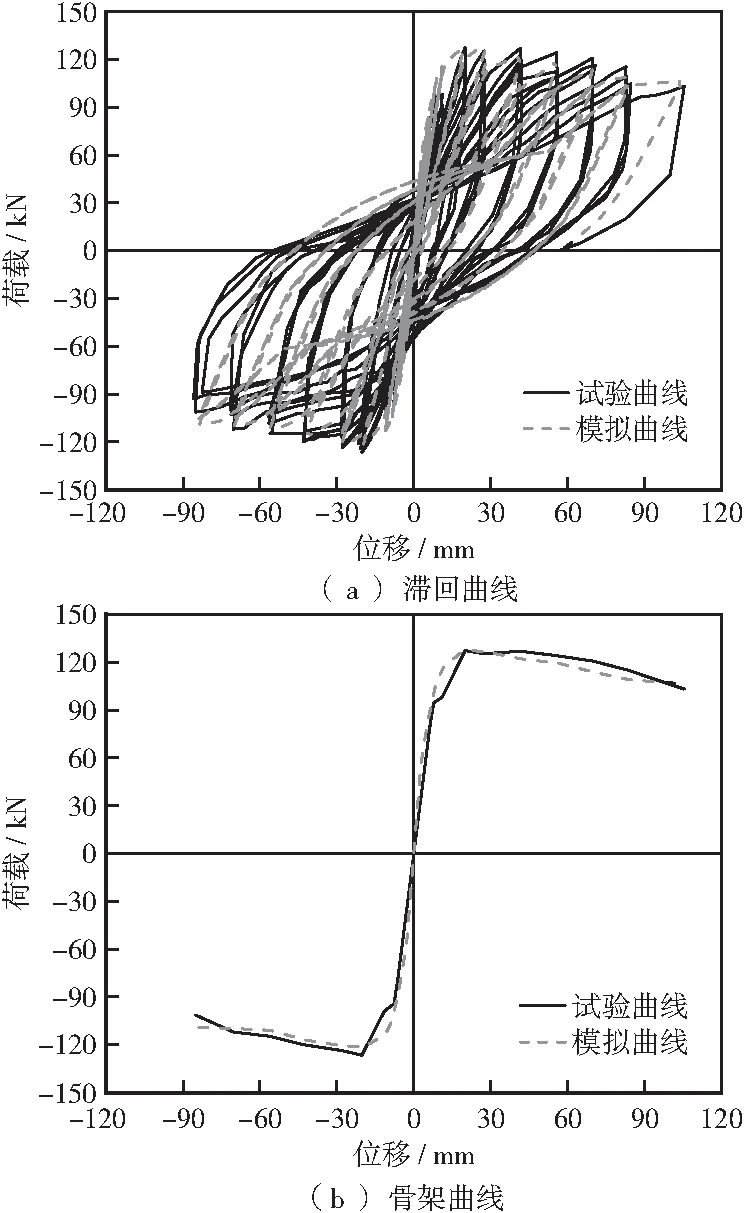
圖6 模擬結果與試驗結果對比Figure 6 Comparison of the predicted and the measured results

3 參數分析

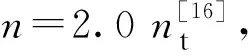
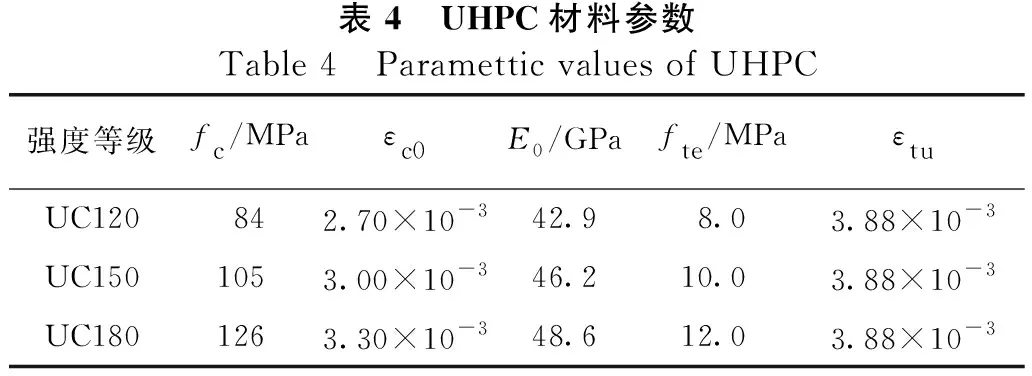
表4 UHPC材料參數Table 4 Paramettic values of UHPC強度等級fc/MPaεc0E0/GPafte/MPaεtuUC120842.70×10-342.98.03.88×10-3UC1501053.00×10-346.210.03.88×10-3UC1801263.30×10-348.612.03.88×10-3

各試件計算結果見表5，試件編號中N、R和S分別表示軸壓比、縱筋配筋率和UHPC強度3個參數，其后的數字表示對應參數的取值；屈服位移按照等能量法[17]計算，極限位移為荷載下降至極限承載能力85%時對應的位移。

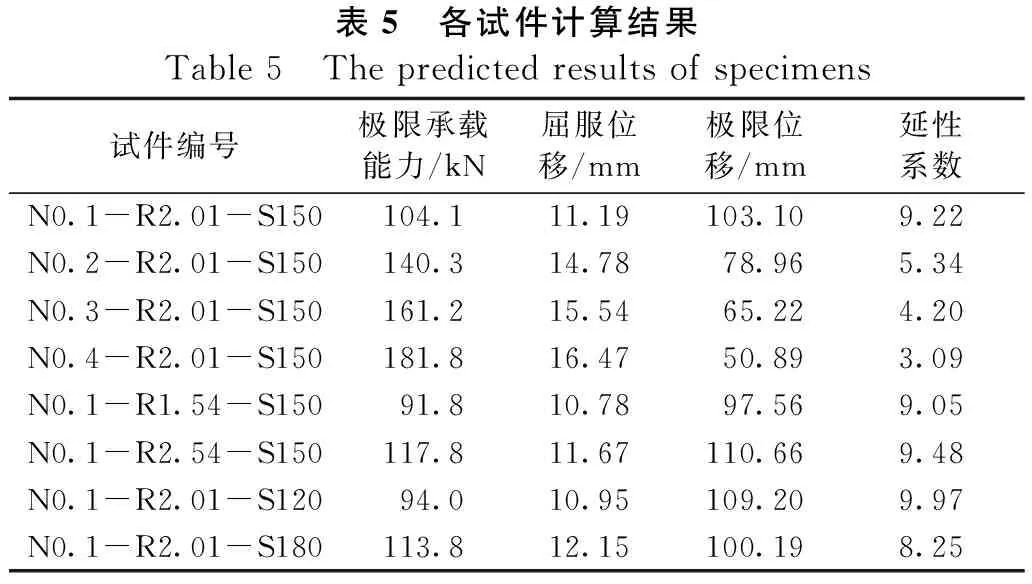
表5 各試件計算結果Table 5 The predicted results of specimens試件編號極限承載能力/kN屈服位移/mm極限位移/mm延性系數N0.1-R2.01-S150104.111.19103.109.22N0.2-R2.01-S150140.314.7878.965.34N0.3-R2.01-S150161.215.5465.224.20N0.4-R2.01-S150181.816.4750.893.09N0.1-R1.54-S15091.810.7897.569.05N0.1-R2.54-S150117.811.67110.669.48N0.1-R2.01-S12094.010.95109.209.97N0.1-R2.01-S180113.812.15100.198.25

所有試件的延性系數均大于3，表現出良好的抗震性能；若以位移延性系數不小于3為目標，則UHPC柱的設計軸壓比限值為0.8。

3.1 軸壓比

軸壓比對試件抗震性能的影響如圖7所示，由于試件模擬骨架曲線正負向基本對稱，故僅取正向骨架曲線進行分析。可知：在加載初期，試件處于彈性狀態，不同軸壓比下試件的初始剛度相同，線性段重合，而軸壓比越大，試件的線性段越長，開裂荷載與位移均越大，骨架曲線下降段越陡峭；軸壓比從0.1增大到0.4，試件的極限承載能力增大75%，屈服位移增大47%，極限位移減小51%，導致延性系數減小66%。

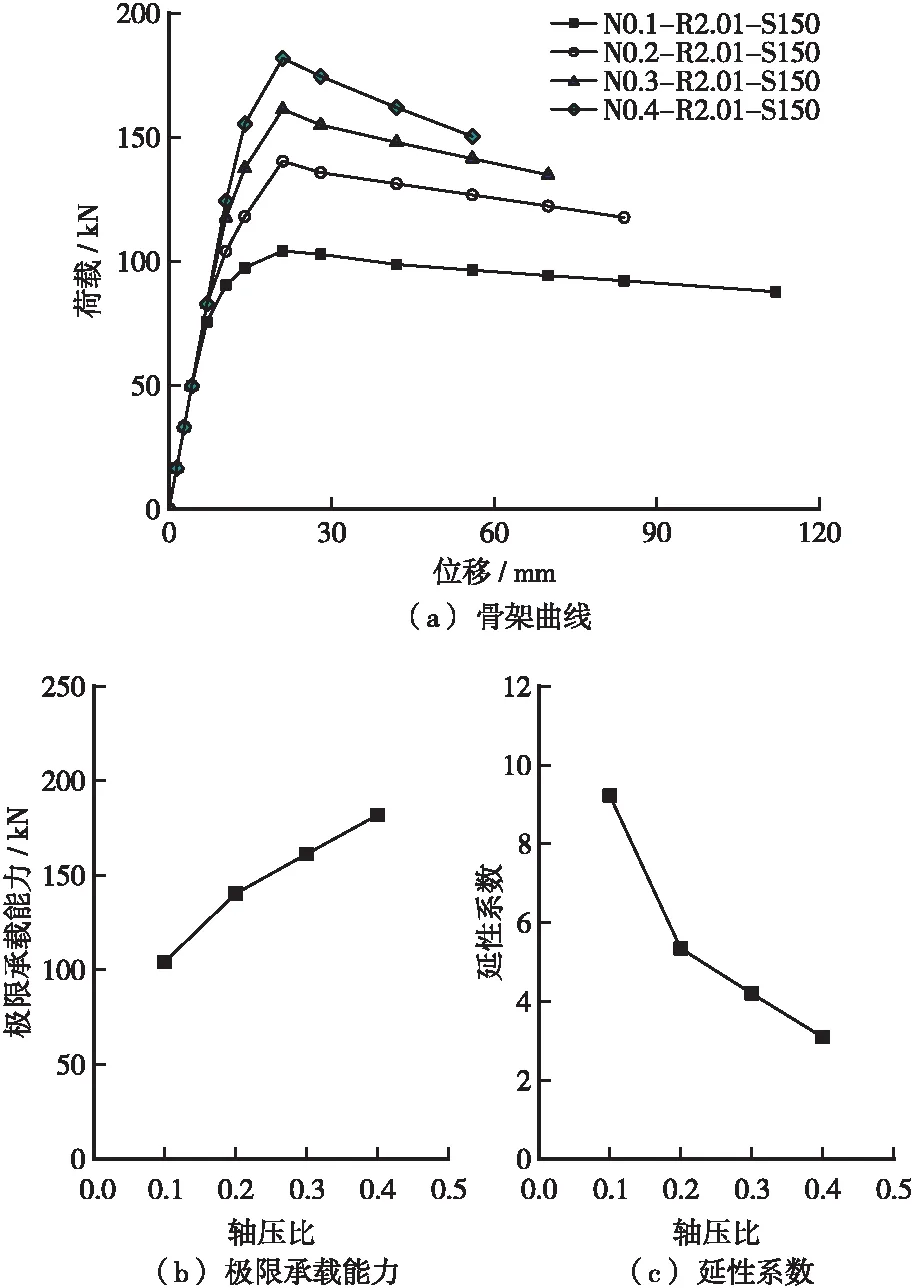
圖7 軸壓比對試件抗震性能的影響Figure 7 Effect of axial loading ratio on seismic performance of specimens

3.2 縱筋配筋率

縱筋配筋率對試件抗震性能的影響如圖8所示。可知：不同縱筋配筋率試件的骨架曲線初始剛度基本相同，試件極限承載能力隨縱筋配筋率的增大而增大；縱筋配筋率從1.54%變為2.54%，增大65%時，試件極限承載能力增大28%，屈服位移增大8%，極限位移增大13%，延性系數增大5%。

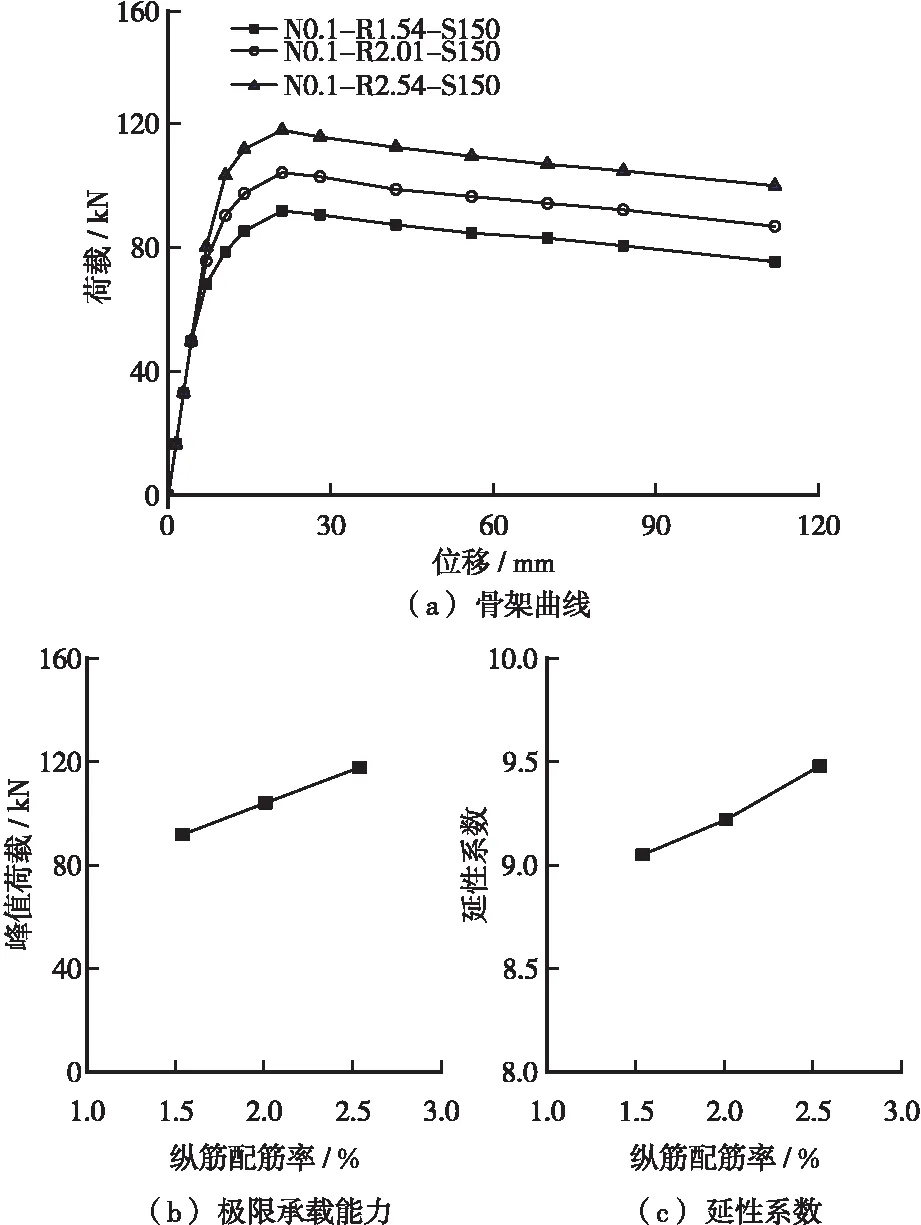
圖8 縱筋配筋率對試件抗震性能的影響Figure 8 Effect of longitudinal reinforcement ratio on seismic performance of specimens

3.3 UHPC強度

UHPC強度對試件抗震性能的影響如圖9所示，可知：隨著UHPC強度等級的增大，試件初始剛度和極限承載能力均增大，UHPC強度等級從UC120提高到UC180，試件初始剛度增大10%，極限承載能力增大21%，屈服位移增大11%，極限位移減小8%，延性系數減小17%；由表5可知，隨著UHPC強度等級的增大，其峰值壓應變增大，極限壓應變減小，由此導致試件的延性降低。

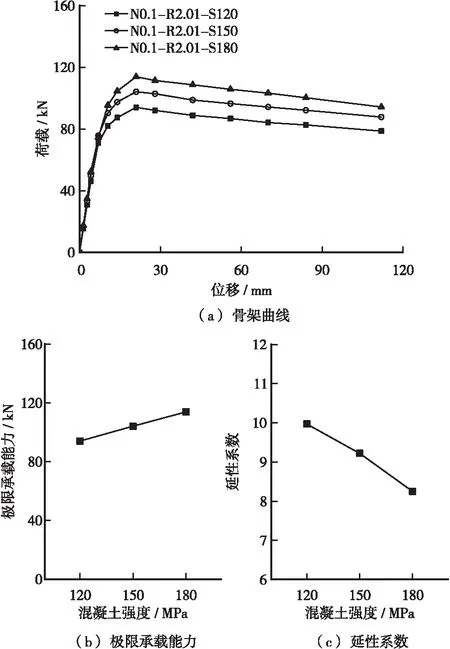
圖9 UHPC強度對試件抗震性能的影響Figure 9 Effect of UHPC strength on seismic performance of specimens

4 結論

采用有限元軟件OpenSees對UHPC柱的抗震性能進行了分析，并以試驗驗證了分析模型的適用性，基于分析結果，得到以下結論：

a.模擬得到的滯回曲線和骨架曲線與試驗結果吻合較好，說明模型對材料本構、截面、單元類型選取合理，數值模型可以較好地模擬UHPC柱的受力性能。

b.軸壓比對試件抗震性能影響顯著，軸壓比從0.1提高到0.4，試件極限承載能力增大75%，極限位移減小51%，延性系數減小66%；縱筋配筋率從1.54%增大到2.54%，試件極限承載能力增大28%，延性系數增大5%；UHPC強度等級從UC120增大到UC180，試件初始剛度增大10%，極限承載能力增大21%，延性系數減小17%。

c.所有試件延性系數均大于3，抗震性能良好；若以位移延性系數不小于3為目標，則UHPC柱的設計軸壓比限值可取為0.8。