冰雪環境雙車道公路彎道車速特征及預測模型

呂 惠， 管星宇， 陳彥旭， 袁 方

(1.上海市城市建設設計研究總院(集團)有限公司， 上海 200125; 2.上海市政工程設計研究總院(集團)有限公司， 上海 200092； 3.同濟大學 道路與交通工程教育部重點實驗室， 上海 201804)

1 概述

我國三、四級公路與等外公路占公路總里程的85%以上[1]，與高等級公路相比，低等級公路技術指標相對較低，平面線型復雜，特別是調研表明山區低等級公路頻繁設置小半徑平曲線，行車安全受較大影響[2]。車輛在通過此類彎道路段時，往往會產生較大的離心力，在冰雪天氣下，道路表面的附著系數急劇降低，路面與輪胎無法提供車輛在正常天氣下行駛的摩擦力，駕駛人對車輛的操控水平下降，駕駛負荷上升，在極端情況下可能發生橫向滑移，進而導致車輛失控，引發事故。WANG[3]等對國外事故的統計分析發現，彎道事故率是直線路段的3倍以上。美國國家公路交通安全管理局[4](NHTSA)公布的事故報告指出，潮濕路面發生車輛沖出路外事故的概率比干燥時增加1.8倍，冰雪路面則增加7倍。因此冰雪天氣彎道路段發生事故的風險較高。

由于在冰雪天氣彎道路段進行自然駕駛實驗難以確保實驗安全，因此國內外對于此類場景下車速預測模型的研究仍然較少，現有研究主要以正常天氣為背景。較多研究結果表明平曲線的行駛車速主要與圓曲線半徑有較強相關性，進而對平曲線運行車速進行建模，并以此作為道路線型連續性與一致性評價的參考依據[3,5-6]，我國《公路項目安全性評價規范》[7]中通過預測運行車速對行駛安全進行評價也是基于此類研究。ZHANG[8]等考慮了不同駕駛人的駕駛風格差異性，使用帶遺忘因子的遞推最小二乘法構建彎道車速模型。LI[9]等提出了一種平曲線路段超速警告系統，平曲線安全車速的計算與道路曲率、道路表面摩阻系數等因素有關。FITZSIMMONS[10]等基于線性混合效應模型構建了城市、農村道路的彎道車速及軌跡預測模型，結論表明入彎時的車速及車輛橫向位置對彎道內車速、軌跡有顯著影響。隨人工智能的發展，也有研究使用BP神經網絡對彎道車速進行預測[11-12]，取得了一定成果。

為重點研究冰雪天氣下彎道路段車速特征并構建相應預測模型，本研究借助同濟大學8自由度駕駛模擬器進行單車駕駛模擬實驗，仿真場景對真實駕駛環境的還原程度高，在解決駕駛實驗安全性問題的同時，保證了實驗數據的有效性，研究結果對于冰雪天氣危險駕駛行為研究及制定限速等管理策略均有指導意義。

2 實驗設計

2.1 研究變量

為研究冰雪天氣下平曲線路段的車速變化規律并構建預測模型，文本選取的主要研究變量分為兩類。第一類為駕駛環境變量，包括天氣環境、圓曲線半徑、轉向；第二類為行駛車速。

環境變量主要針對冰雪天氣，同時考慮正常天氣環境作為對比，因此共設置晴天、雨天、雪天、結冰4種場景，冰雪對彎道行駛安全的影響主要為路面附著系數f的降低，參考現有研究成果[13]，不同天氣對應的f取值如表1所示。

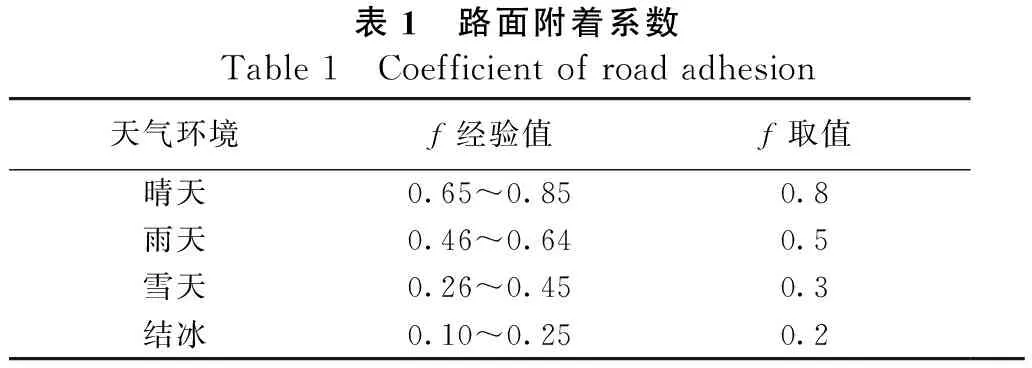
表1 路面附著系數Table 1 Coefficient of road adhesion天氣環境f經驗值f取值晴天0.65～0.850.8雨天0.46～0.640.5雪天0.26～0.450.3結冰0.10～0.250.2

雙車道公路通常為低等級公路，考慮到冰雪環境，最大超高取6%，圓曲線半徑設置參考《公路路線設計規范》[14]中20～60 km/h設計車速范圍內各級車速對應的圓曲線最小半徑極限值，確定為15、35、60、135、270 m。

車速變量選用平曲線5個要素點位置的車速，如圖1所示，以及圓曲行駛過程中的平均車速。

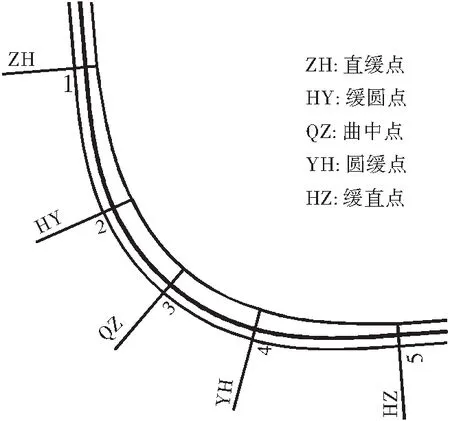
圖1 車速采集點Figure 1 Collection points of vehicle speed

本文研究過程中使用的全部變量與對應描述見表2。

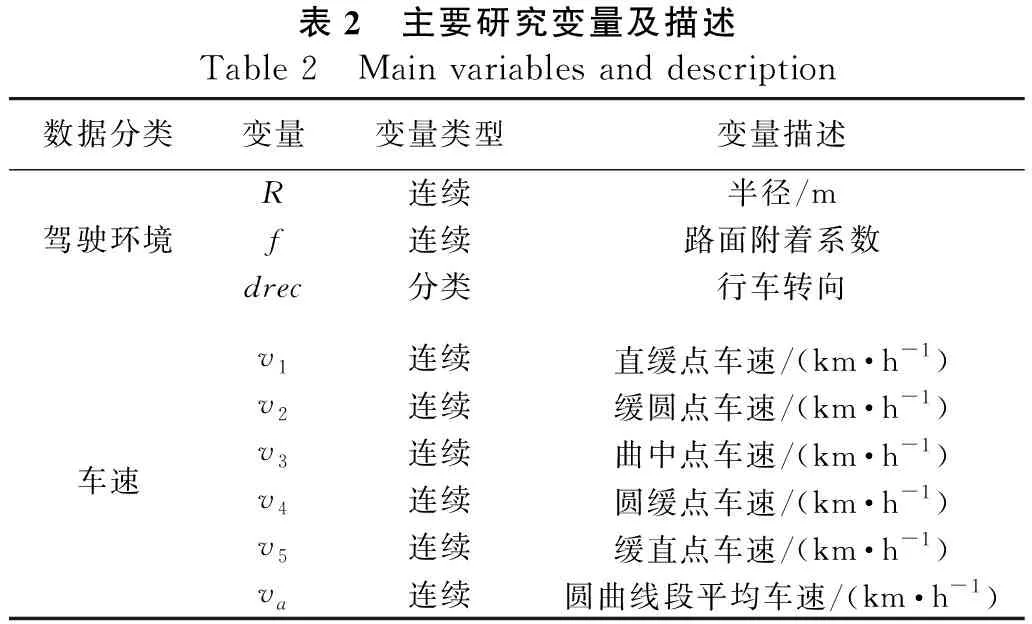
表2 主要研究變量及描述Table 2 Main variables and description數據分類變量變量類型變量描述R連續半徑/m駕駛環境f連續路面附著系數drec分類行車轉向v1連續直緩點車速/(km·h-1)v2連續緩圓點車速/(km·h-1)車速v3連續曲中點車速/(km·h-1)v4連續圓緩點車速/(km·h-1)v5連續緩直點車速/(km·h-1)va連續圓曲線段平均車速/(km·h-1)

2.2 實驗設備

本研究采用同濟大學8自由度駕駛模擬器完成實驗，駕駛模擬器由駕駛艙、液壓系統與底部運動系統組成，如圖2所示，駕駛艙受液壓系統推力在空間中有6個自由度，底部平動系統有2個自由度。駕駛艙內部配有一輛無引擎的1∶1實車，頂部安裝有5臺投影儀，并與環形幕布構成成像系統，如圖3所示。

圖2 8自由度駕駛模擬器Figure 2 8 Degrees of freedom driving simulator

圖3 駕駛模擬器內部Figure 3 Interior of driving simulator

實驗過程中設備可采集車速、路面附著系數、橫向位置、道路半徑、轉向等數據，采樣率設定為10 Hz。

2.3 實驗場景設計

道路仿真場景按天氣環境共分4個子路段，天氣及相應的附著系數為無序布置，每個子路段線形指標相同，均包含前文所述的5組不同半徑構成的平曲線，如圖4所示，實驗道路全長約7.6 km。

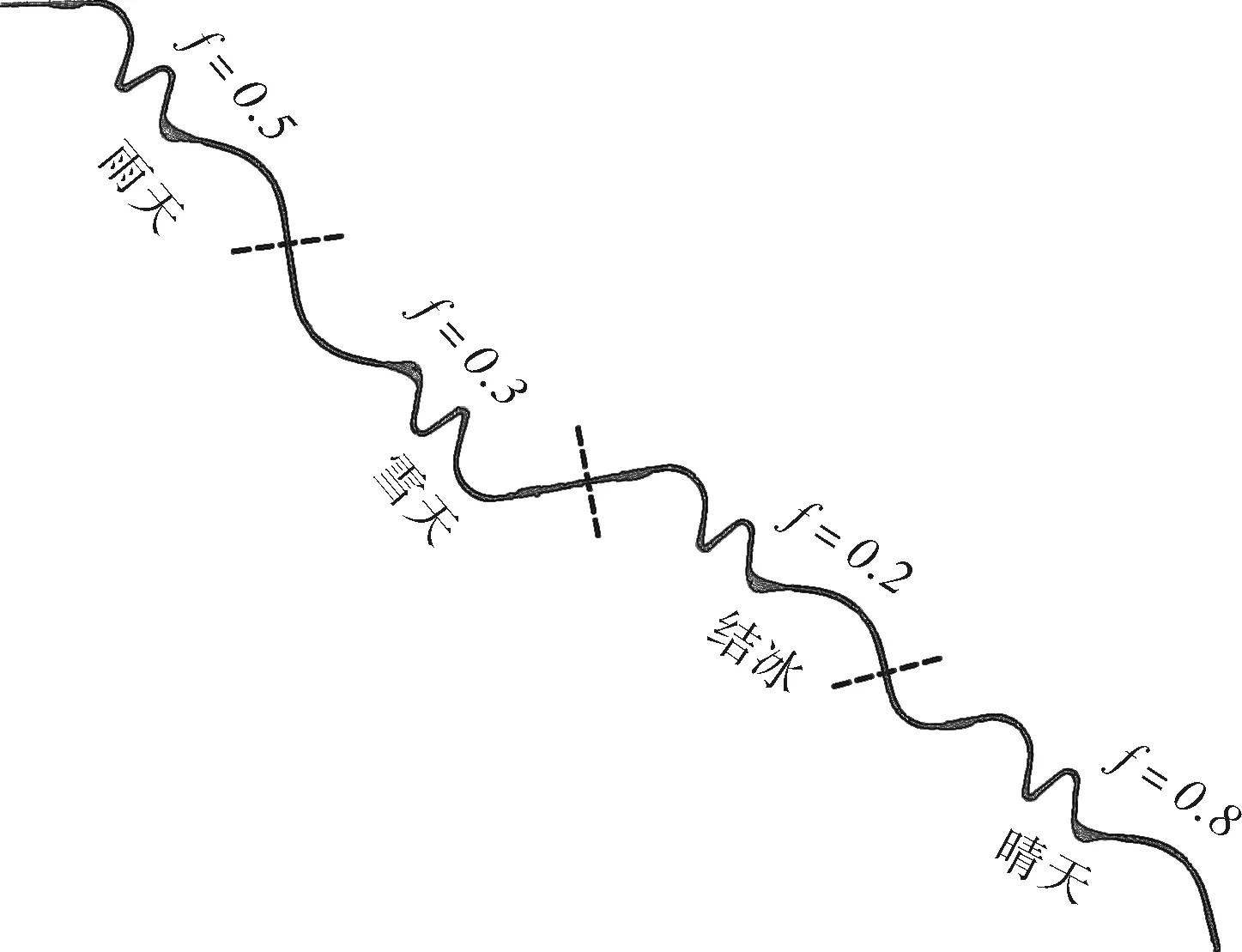
圖4 駕駛模擬實驗道路平面設計Figure 4 Road plane dsign for simulated scenario

道路橫斷面為標準7.5 m寬雙車道，圓曲線超高、加寬均參照規范值設置，本研究主要針對彎道路段，為減小道路縱坡對實驗的影響，縱坡設置為0。圖5為使用道路設計軟件及模擬駕駛軟件構建的仿真場景。

晴天

2.4 實驗人員

被試者共32名，均持有C1駕駛證，駕齡在3～12 a之間，平均駕齡為5.4 a；年齡在25～47歲之間，平均年齡為31.6歲。

2.5 實驗過程

由于駕駛模擬器對冰雪天氣的仿真與真實環境仍存在一定差別，在進行正式實驗前，首先讓被試者在試驗路段行駛以獲得濕滑路面的模擬駕駛體驗，最大程度保證實驗可靠性。考慮到駕駛人過彎時車速為自主選擇行為，且因部分低等級公路缺乏限速設施，因此實驗過程僅提示駕駛人山區公路注意控制車速，不宜超過60 km/h，保證駕駛安全。排除部分無效數據后，實驗過程中共獲取了589組彎道行駛的有效數據。

3 彎道車速特征

3.1 不同駕駛場景下彎道車速的分布規律

為分析車速在不同駕駛環境下的變化特征，在駕駛模擬實驗獲得的所有數據中，以各圓曲線路段的平均車速va作為代表車速，將va關于R、f的變化情況繪制于圖6等高線圖中(已平滑處理)。

圖6 平均車速在不同駕駛場景下的分布Figure 6 Distribution of average speed in different driving scenarios

觀察車速分布的整體趨勢可以發現，圓曲線路段的行駛車速隨附著系數升高、半徑增加而逐步增大，在R=270 m、f=0.8時，過彎的平均車速達到50 km/h，而在R=15 m、f=0.2的極端條件下，平均車速會降低至20 km/h以下。此外，隨半徑減小，摩擦系數對車速的影響逐漸下降，說明圓曲線半徑對過彎車速的影響相對更大。

3.2 彎道內的車速變化規律

通過分析平曲線要素點對應的車速，在R≤60 m時，車速存在明顯的減速段與加速段，整體呈現U型的變化規律，車速極小值一般出現在曲中點至圓緩點間；當R≥135 m時，車速的減速段與加速段不再明顯。冰雪天氣下彎道內的行駛車速明顯低于晴雨天氣，且普遍低于極限最小半徑對應的設計車速，如圖7所示。

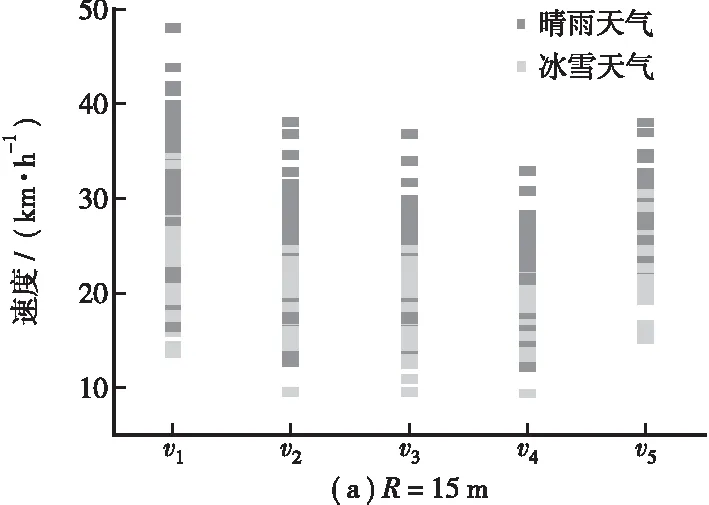
圖7 平曲線上各要素點車速的變化規律

4 主要變量分析

4.1 偏相關性分析

對可能影響車速的主要變量進行Pearson偏相關性分析，表3為各圓曲線va與R、f、drec的偏相關性分析，結果表明圓曲線路段的平均車速與圓曲線半徑相關性最高，其次為路面附著系數，與轉向相關性較低。

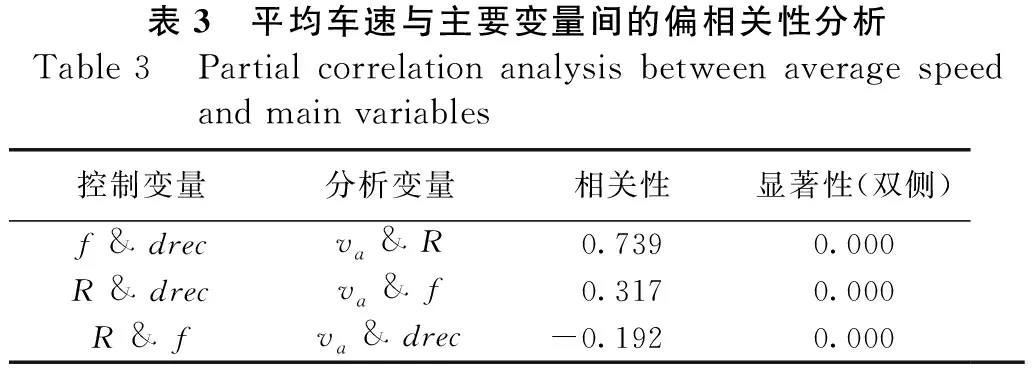
表3 平均車速與主要變量間的偏相關性分析Table 3 Partial correlation analysis between average speed and main variables控制變量分析變量相關性顯著性(雙側)f & drecva & R0.7390.000R & drecva & f0.3170.000R & fva & drec-0.1920.000

4.2 車速與半徑的曲線關系

通過SPSS曲線估計分析va與R的數學關系如下:F統計量顯著性為0.000,小于0.05;擬合優度R2=0.621；F為1 011.416；確定va與R呈對數增長的關系，與以往研究結果基本一致[7,15]。

以va為縱坐標，R為橫坐標，繪制所有車速樣本的散點圖與對數擬合曲線，結果如圖8所示。

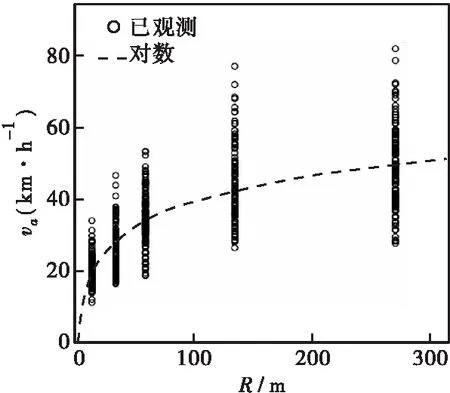
圖8 散點圖與對數曲線擬合Figure 8 Scatter and logarithmic curve fitting

分別對晴雨、冰雪天氣下va、v1～v5與半徑的關系進行相同分析，結果表明不同場景下平曲線上各點車速都與半徑呈對數增長的關系，且相互間存在較強的線性相關性。

4.3 車速在不同附著系數下的分布差異

以va代表圓曲線路段行駛車速，不同附著系數下樣本的正態性檢驗與方差檢驗表示各組樣本均不滿足正態分布與方差齊性，因此使用Kruskal-Wallis秩和檢驗對各組樣本的差異性進行判斷，結果表明va在不同附著系數下的分布有顯著差異，如表4所示。

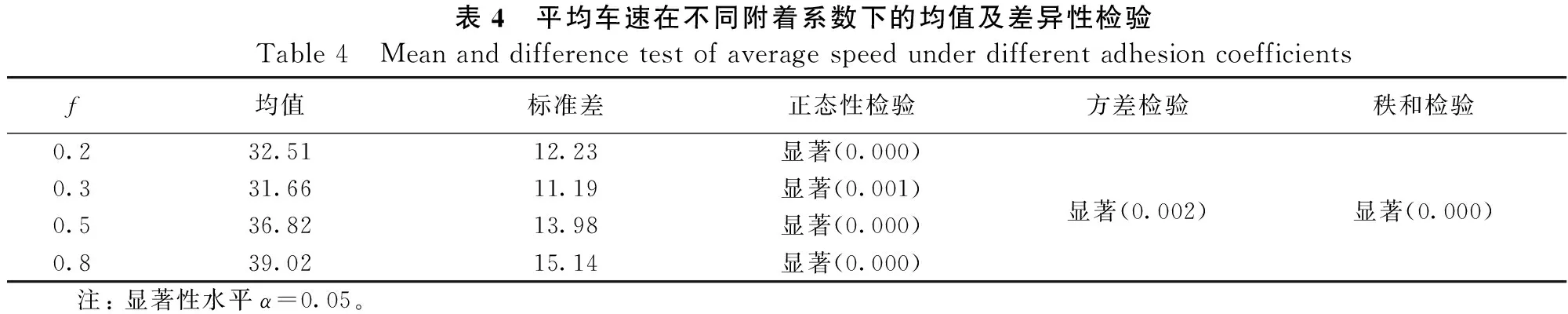
表4 平均車速在不同附著系數下的均值及差異性檢驗Table 4 Mean and difference test of average speed under different adhesion coefficientsf均值標準差正態性檢驗方差檢驗秩和檢驗0.232.5112.23顯著(0.000)0.331.6611.19顯著(0.001)顯著(0.002)顯著(0.000)0.536.8213.98顯著(0.000)0.839.0215.14顯著(0.000) 注: 顯著性水平α=0.05。

進一步分析平均車速在4類附著系數下的組間差異，對平均車速進行平均秩檢驗，結果如表5所示，在4類附著系數下共有2個子集，分別為冰雪與晴雨場景，2個子集間存在較大統計學差異，而子集內部平均秩檢驗顯著性大于0.1，表示子集內差異性小。因此，車速分別在冰雪、晴雨2個組合場景之間表現出較大差異，應分別在冰雪、晴雨2個組合場景中構建車速預測模型。

表5 平均車速的齊性子集Table 5 Homogeneous subsets of average speed子集不同附著系數樣本0.20.30.50.8檢驗統計量調整后的顯著性(雙側)1260.115266.5590.1010.9382318.800341.0201.2060.470

4.4 車速在不同轉向下的分布差異

使用Kruskal-Wallis秩和檢驗對平均車速在不同轉向下的差異性進行分析，結果表明車速在不同轉向下無顯著差異，如表6所示，同時結合表3分析結果，可知車速與曲線轉向的相關性較低，因此預測模型不考慮將轉向作為預測變量。

表6 平均車速在在不同轉向下的均值及差異性檢驗Table 6 Mean and difference test of average speed under different driving directionsdrec均值標準差正態性檢驗方差檢驗秩和檢驗右轉33.212.53顯著(0.002)顯著(0.029)不顯著(0.151)左轉30.9710.75顯著(0.000)注: 顯著性水平α=0.05。

5 平曲線車速預測模型

5.1 模型構建

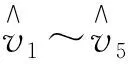
(1)

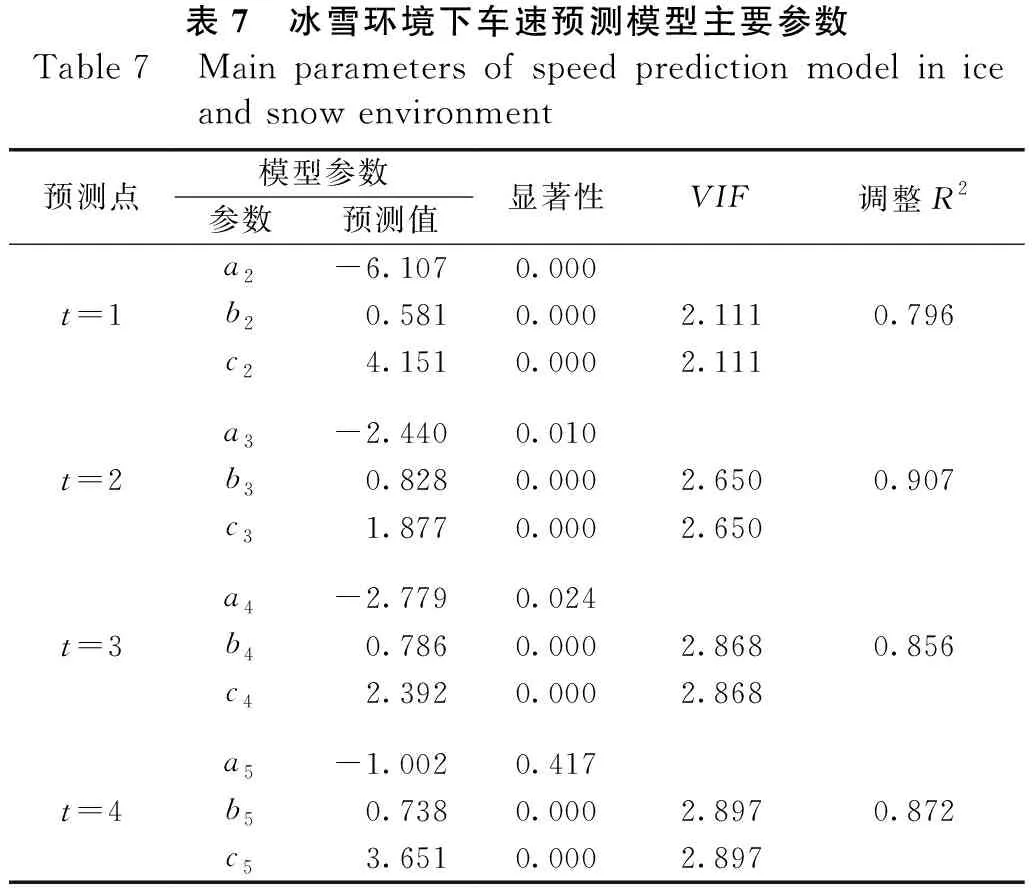
表7 冰雪環境下車速預測模型主要參數Table 7 Main parameters of speed prediction model in ice and snow environment預測點模型參數參數預測值顯著性VIF調整R2a2-6.1070.000t=1b20.5810.0002.1110.796c24.1510.0002.111a3-2.4400.010t=2b30.8280.0002.6500.907c31.8770.0002.650a4-2.7790.024t=3b40.7860.0002.8680.856c42.3920.0002.868a5-1.0020.417t=4b50.7380.0002.8970.872c53.6510.0002.897

對模型的自變量顯著性進行獨立樣本T檢驗，表中結果均小于0.05，說明自變量對預測車速具有顯著影響，使用方差膨脹因子VIF檢驗自變量共線性，表中VIF<5，表示自變量間不存在共線問題，結合調整后的R2對模型擬合優度進行評價，由R2>0.7可知各點車速回歸精度較好。

在獲得平曲線上各要素點車速預測結果后，本文假設車速為連續均勻變化，各要素點間的車速以三次方樣條插值確定。

5.2 模型檢驗

設實驗中任一平曲線共有n個行駛車速采樣點，以平曲線路段的平均誤差率CMER(Curve Mean Error Rate)對平曲線車速預測模型的精度進行評價，如式(2)所示：

(2)

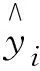
當車輛以較高速度行駛時，單獨使用CMER無法完全體現預測精度，因此還需結合預測值與實際值的曲線相關系數對模型進行綜合評價，通過matlab對模型與實際值的相關系數進行計算，得到本模型的總體相關系數為0.618。綜合分析表明，模型具有一定適用性。

6 結語

a.車輛在曲線路段的行駛車速隨半徑增加、路面附著系數增大而增大，在平曲線行駛過程中，存在明顯的減速段與加速段，車速極小值通常位于曲中點至圓緩點之間。

b.冰雪環境下，駕駛人趨于保守，車輛在彎道內的行駛車速明顯低于晴雨天氣，且普遍低于極限最小半徑對應的設計車速。

c.圓曲線行駛車速與半徑呈對數增長關系，與轉向無明顯相關性，各要素點的車速之間存在較強線性相關性。