帶鋼短柱UHPC夾芯板抗彎性能試驗研究與有限元分析

李 衛, 晏班夫, 邵旭東, 余加勇

(1.湖南大學 風工程與橋梁工程湖南省重點實驗室， 湖南 長沙 410082; 2.中交公路規劃設計院有限公司， 北京 100088)

UHPC(超高性能混凝土)夾芯板是一種以水泥、細砂、硅灰、高效減水劑、鋼(耐堿玻璃纖維)等為主要原料的新型夾芯板結構，具有結構質量輕、傳熱能力差、耐久性優勢明顯等諸多優點。UHPC由于其特殊的原料具有以下力學性能優勢：超高強度、超低吸水率、超強耐久性和耐侵蝕性能[1-2]。目前，UHPC多用于公路橋梁，海洋工程、建筑工程、結構加固維修等。

針對普通混凝土夾芯板抗彎性能方面的研究較多。例如，李硯波[3]等對普通混凝土夾芯板進行了抗彎試驗研究，并對相關規范中的受彎構件計算公式進行了補充。俞劍勇[4]等建立了CS板的非線性有限元計算模型，分析了CS板結構幾何條件的變化對CS板力學性能的影響。而就目前來說，對于UHPC夾芯板抗彎性能的研究還很少。因此對UHPC夾芯板進行研究以獲得其力學性能就顯得尤為重要。

本文設計并制作了2片UHPC夾芯板，并同時結合靜力試驗與有限元分析2種方法對其力學性能進行了研究。研究中驗證了不同夾芯板的極限承載力及破壞模式，在驗證有限元模型準確可信的前提下，對模型進行了參數分析，掌握了底板主筋配筋率、頂底板厚度、板高度以及短柱尺寸對UHPC夾芯板抗彎性能的影響規律。

1 模型試驗

1.1 試驗板設計

試驗共制作了2塊夾芯板，頂底板的厚度均為5 cm，寬度40 cm，夾芯板總的高度為25 cm，夾芯板層的厚度為15 cm。為了方便敘述，在此分別將2塊板定義為SP1與SP2，其中試件SP1的長度為240 cm，不銹鋼短柱高25 cm，外徑6 cm，壁厚為0.5 cm，短柱的橫向間距為20 cm，縱向間距20 cm；試件SP2的長度為260 cm，不銹鋼短柱高25 cm，外徑4.8 cm，壁厚為0.3 cm，短柱的橫向間距為20 cm，縱向間距30 cm。其中頂底板受力鋼筋直徑分別為8 mm和14 mm，間距為10 cm；頂底板內采用直徑為6 mm的分布鋼筋來固定受力鋼筋的位置，其間距為對應不銹鋼短柱的縱向距離。各試驗板的主要設計參數如表1所示，試驗板立面圖如圖1所示，試驗板配筋圖如圖2所示。

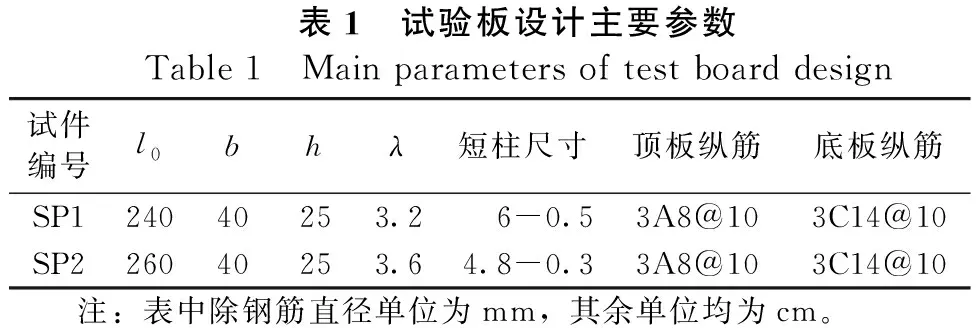
表1 試驗板設計主要參數Table 1 Main parameters of test board design試件編號l0bhλ短柱尺寸頂板縱筋底板縱筋SP124040253.26-0.53A8@103C14@10SP226040253.64.8-0.33A8@103C14@10注:表中除鋼筋直徑單位為mm,其余單位均為cm。

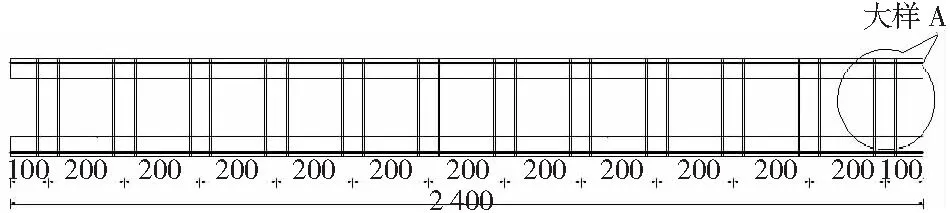
(a) SP1板

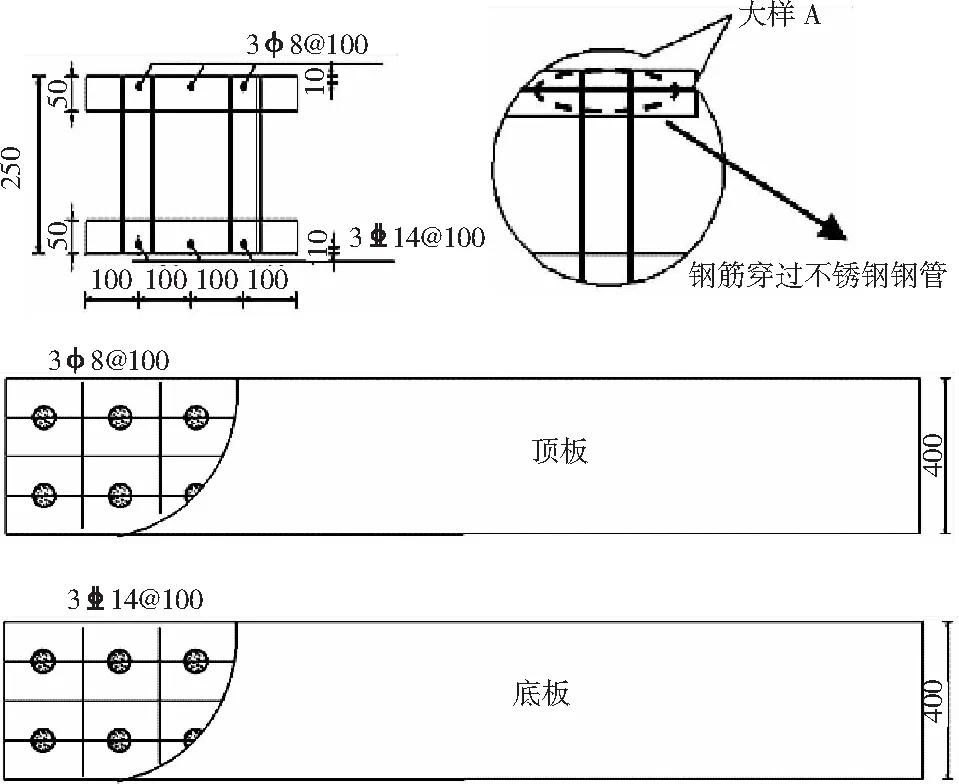
圖2 試驗板配筋圖(SP1、SP2)(單位:mm)

1.2 UHPC力學性能

頂底板UHPC以及短柱中內填UHPC均為同種材料，對材性試塊與試驗模型進行同步養護，在正式加載前進行材料性能測試，測試結果如下：立方體抗壓強度161 MPa,棱柱體抗折強度25.2 MPa,彈性模量Ec為48.6 ×104MPa。

1.3 測試內容及加載模式

本試驗采用4點加載方案，剪跨比均大于3，模型均采用簡支支撐。為了保證模型邊界約束的可靠性，在試驗模型的一側采用固定鉸支座，另一側采用滾動支座。各試驗板的純彎段均為60 cm，試件SP1剪跨段長80 cm，試件SP2剪跨段長90 cm。在板頂底表面的純彎段內3個截面上布有混凝土應變片，對應頂底板側面同一位置也布有混凝土應變片，在支座處頂板附近用千分表測量支座處的撓度，沿板長加載點以及跨中3個位置點處布置有百分表用來測量板的撓度，同時為了測量頂底板水平方向的滑移，在短柱與頂底板交匯處的剪跨段板側噴有散斑點，散斑點的具體位置如圖3所示，現場試驗相機位置如圖4所示。

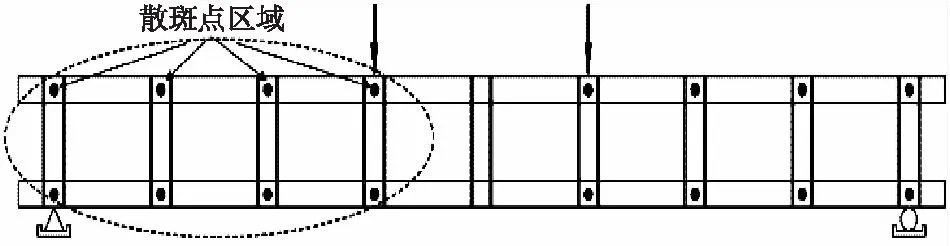
圖3 散斑點區域示意圖Figure 3 Schematic diagram of scattered spots

圖4 相機布置圖Figure 4 Camera layout

試驗過程中，應變數據用靜態數據采集儀采集。加載裝置為100 t手搖油壓千斤頂，荷載由壓力傳感器測量。裂縫寬度采用裂縫寬度觀測儀進行量測，其測量的精度為0.01 mm。現場試驗加載裝置如圖5所示，試驗加載方式以及測點位置如圖6所示。

圖5 試驗現場加載裝置圖Figure 5 Test site loading device diagram

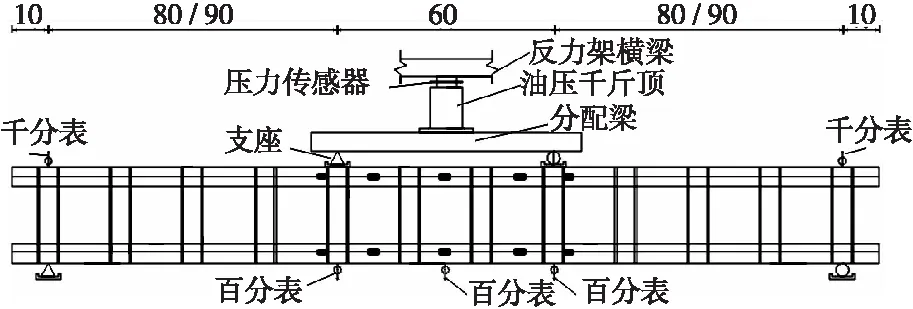
圖6 試驗加載及測點布置Figure 6 Test loading and layout of measuring points

1.4 試驗加載制度

在正式加載之前，首先對試件進行預加載，預加載的目的是為了檢查儀器設備是否完好，預加載結束后正常卸載，之后開始正式加載。

正式加載時采用分級加載，每級荷載大約為預計極限荷載的5%，待加載到預估開裂荷載時減小荷載步。等試件開裂后，仍按照原先的荷載步進行加載，每級荷載持續5 min左右，待達到破壞荷載的80%時，減少荷載步，直至試件破壞。每級荷載穩定后記錄相關數據。

2 試驗結果及分析

2.1 荷載-位移曲線

各試件荷載位移曲線如圖7所示，由于試件的剪跨段長度不同，因此將縱坐標荷載轉換成對應板跨中彎矩。各試件主要試驗結果見表2。圖7中可以看出各試件整個試驗加載過程，試件SP1與試件SP2有著較為明顯的區別。

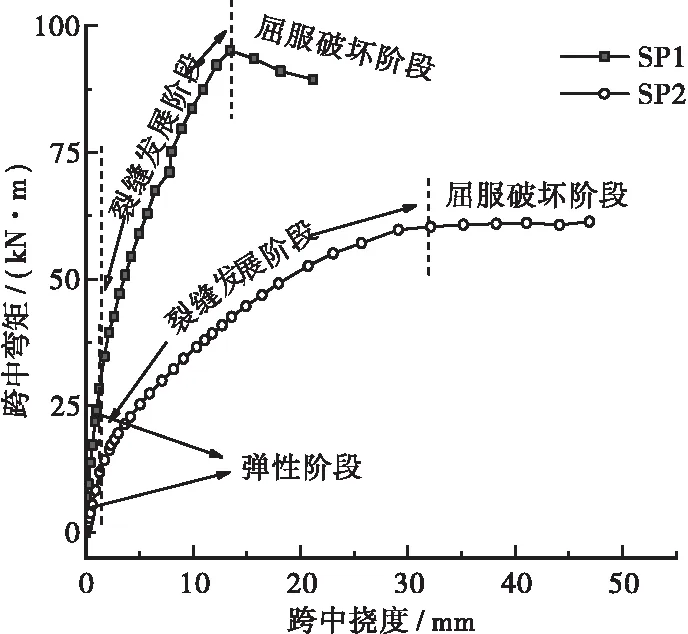
圖7 荷載-跨中撓度曲線Figure 7 Load-Mid-span Deflection Curves

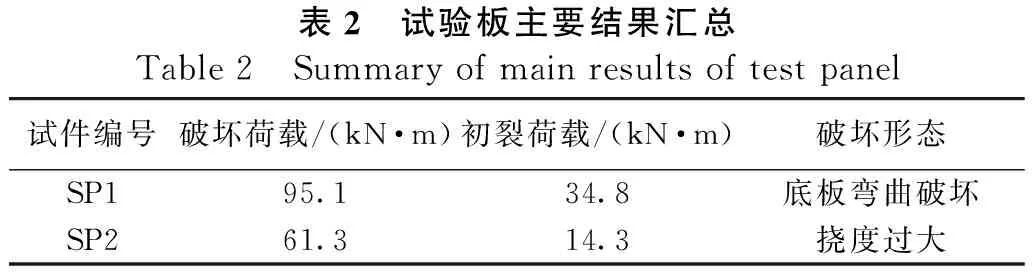
表2 試驗板主要結果匯總Table 2 Summary of main results of test panel試件編號破壞荷載/(kN·m)初裂荷載/(kN·m)破壞形態SP195.134.8底板彎曲破壞SP261.314.3撓度過大

由圖7可知，試件在加載破壞過程中均經歷以下3個階段，即線彈性階段、裂縫發展階段、屈服破壞階段。在線彈性階段，試件均未出現裂縫，荷載與撓度呈線性關系，試件的剛度幾乎保持不變，但二者在彈性階段的剛度略有差異；當裂縫開始處于發展趨勢后，截面剛度均有不同程度降低，在該階段很長的一段加載時間內，UHPC底板出現不同程度的開裂，裂縫的數量、裂縫的寬度和長度不斷擴展，同時也有部分細小的裂縫出現，該階段持續至底板鋼筋屈服；在鋼筋屈服后，試件撓度增長較快，經歷很短的屈服強化階段后各試件進入破壞階段。

相較于試件SP1，試件SP2在裂縫出現后剛度下降較為明顯，撓度增長更快，同時試件SP2在裂縫發展階段曲線較為平緩，而試件SP1在進入持荷破壞階段時有明顯的拐點。這與試件的裂縫分布有著很大的關聯，試件SP1主裂縫集中在底板跨中區域，裂縫分布較密集，在鋼筋屈服之前試件能夠維持較高的剛度，鋼筋屈服后試件剛度下降明顯。試件SP2由于其裂縫分布的較為分散，裂縫分布于剪跨段短柱附近的底板處，試件剛度隨著裂縫離散增加而緩慢下降，導致曲線在該階段較為平緩。各試件在加載后期，底板鋼筋均屈服，試件SP1的裂縫寬度不斷增加，隨著鋼纖維拔出的“噼啪”聲，荷載不增反降，試件迅速進入破壞階段；試件SP2未出現鋼纖維拔出的“噼啪”聲，荷載緩慢增加，撓度增長迅速，最終試件因為撓度過大而無法承載。

2.2 荷載-滑移曲線

各試件在彈性階段的滑移分布曲線如圖8所示。

從滑移的分布曲線可以看出，板跨中滑移量幾乎為0，從跨中向支座兩側滑移量逐漸增加，試件SP1的最大滑移量為0.05 mm，試件SP2的最大滑移量為0.09 mm，這是因為試件SP1的短柱直徑較大，短柱的縱向間距較小，板的抗滑移剛度較大，整體性能較強，試件的滑移量較小。

2.3 破壞形態

SP1板最終破壞形態如圖9(a)所示，可以看出最終破壞時底板純彎段有一條非常明顯的主裂縫和少數密集次裂縫，裂縫最大寬度超過1 cm，試件頂板上緣未被壓碎，但底板鋼筋已經屈服。在加載后期時，底板鋼筋屈服后純彎段裂縫寬度急劇增長，底板主裂縫處鋼纖維被拔出，試件不能繼續承載。

SP2板最終破壞形態如圖9(b)所示，其破壞形態為剪跨段短柱附近的UHPC密集開裂，整體來看裂縫分布較為分散，主裂縫不明顯，位于加載點附近的頂板UHPC有輕微壓碎現象，底板鋼筋屈服。在試驗后期，雖然荷載能夠保持穩定，但跨中撓度持續增大，試件最終因撓度過大而無法繼續承載。

2.4 試驗結果分析

綜合上述試驗結果，可做出以下分析。

a.試件SP1由于其短柱直徑較大，分布較密，試件在承載力、抗裂性能、剛度等受彎性能均優于試件SP2，但試件SP2延性更好。

b.試件SP1與試件SP2破壞形態及裂縫發展說明，短柱直徑大小，分布的密集程度主要會影響試件的抗滑移剛度，從而影響試件的整體復合程度，影響試件的裂縫發展過程以及破壞形態。試件的抗滑移剛度越大，試件的整體性能就越強，試件的裂縫分布以及破壞形態更加接近普通混凝土板受彎破壞；當試件的抗滑移剛度較小時，試件的整體性能低，短柱處的集中應力越明顯，裂縫分布也會比較分散。

3 有限元模型建立

為了研究帶鋼短柱UHPC夾芯板4點抗彎試驗的全過程，通過有限元分析軟件ABAQUS建立模型，采用分離式建模方式對上述2塊夾芯板試件進行數值模擬。其中為了避免加載點以及支座處出現應力集中現象，在模型中頂底板的相應區域建立鋼塊與面板綁定。

3.1 單元類型

本文中的UHPC、鋼塊、不銹鋼短柱均采用實體單元C3D8R來模擬，鋼筋采用桁架單元T3D2模擬。

3.2 材料本構模型

對于混凝土抗彎試件在單調荷載的作用下，聶建國[6]等通過研究發現塑性損傷模型能夠模擬得更加準確，模擬結果與試驗更加接近。同時該模型能夠分別考慮材料的受拉與受壓性能，其主要失效原理是材料的受拉開裂破壞以及受壓壓碎破壞[7-8]。因此本文中的UHPC采用混凝土損傷塑性(CDP)模型，模型中的其他參數如下： 膨脹角30°，偏心率0.1，雙軸極限抗壓/單軸極限抗壓1.16不變應比為0.666 7，粘性系數0.001。

受壓本構采用文獻[9]中提出的相應的UHPC受壓本構關系式，即:

(1)

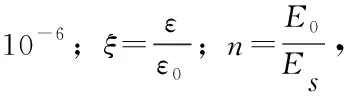
受拉本構采用文獻[10]中提出的UHPC受拉本構關系式，即:

(2)

式中：fct為應變硬化階段平均應力，取8 MPa；εca為線性拐點處的應變，取εca=199×10-6;εpc為最大應變，取1 914×10-6。

最終通過公式計算、數據整理得到UHPC拉壓本構關系曲線，如圖10所示。

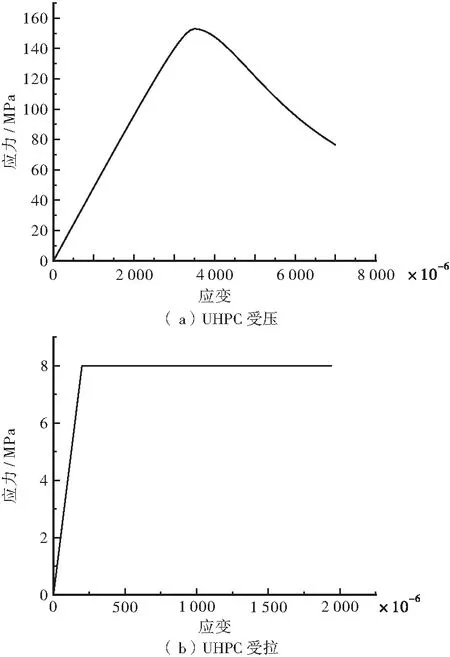
圖10 UHPC本構關系曲線Figure 10 Constitutive relationship curve of UHPC

鋼筋的本構模型如圖11所示，鋼筋型號為HRB400，參考相關文獻取屈服強度fy=482 MPa；彈性模量Es=200 GPa；泊松比μ=0.3。

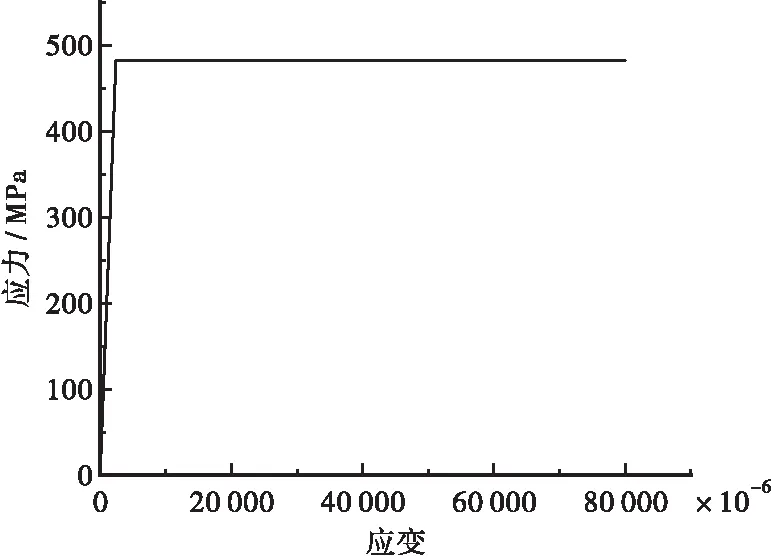
圖11 鋼筋本構關系曲線Figure 11 Constitutive relationship curve of Reinforcement

由于不銹鋼材料的特殊性，其本構模型中的屈服點不顯著，通常用塑性應變為0.2%對應的應力作為其屈服強度，本文參考文獻[11-12]得到不銹鋼的力學性能為E0=200 GPa；σ0.2=230 MPa；σu=540 MPa，對應的本構關系式為：

(3)

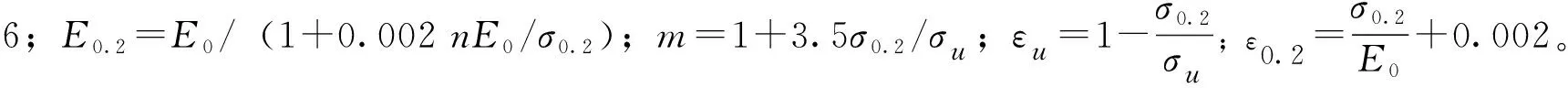
最終通過公式計算、數據整理得到不銹鋼材料的本構關系曲線，如圖12所示。

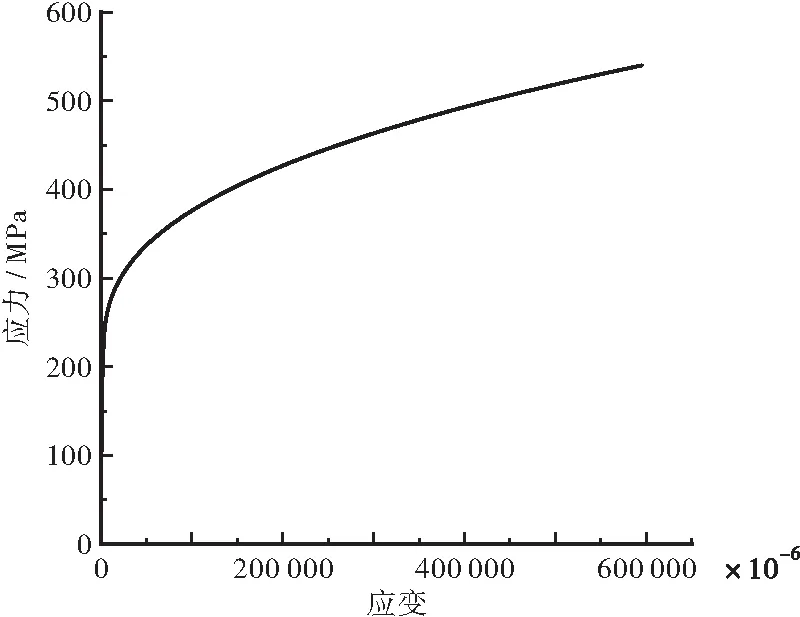
圖12 不銹鋼本構關系曲線Figure 12 Constitutive relationship curve of stainless steel

3.3 相互作用定義

在模型中存在不銹鋼短柱與UHPC、鋼筋與UHPC以及支座、墊塊與UHPC之間的相互作用。

不銹鋼短柱埋在UHPC面板內的那一部分與UHPC約束關系采用嵌入(Embedded)。

鋼筋與UHPC的約束關系采用嵌入(Embedded)約束。

支座與UHPC面板、墊塊與UHPC面板采用綁定(Tie)約束，該約束能夠使得模型中的兩部分不產生相對運動。

3.4 計算結果對比分析

將有限元分析得到的試件荷載跨中撓度、滑移分布曲線、破壞形態等結果與試驗值進行比較，檢驗有限元計算的合理性，為后續參數分析提供支持打下基礎。

3.4.1荷載-跨中撓度曲線

圖13中的對比曲線可以看出，2條曲線吻合得較好且趨勢基本能夠保持一致。各曲線均存在2個較明顯的拐點，圖中A、B兩點，其中A點為板的開裂點，B為鋼筋屈服點。在A點之前的彈性階段，荷載與跨中撓度呈線性關系，有限元計算值與試驗值幾乎保持一致。在A點以后的裂縫發展階段，曲線出現了不同程度的偏差，主要原因是試驗加載過程中存在偏載的可能，板體傾向于先開裂一側，導致百分表在測量位移數據時發生不垂直的位移變化；再有就是有限元模擬的材料本構、邊界條件與實際情況存在偏差。B點以后的屈服破壞階段，試件的剛度下降明顯直到試件完全破壞。將A、B兩點的試驗值與有限元計算值匯總于表3。總的來說，兩條曲線偏差不多吻合較好，這也說明了通過有限元模擬分析的可靠性。

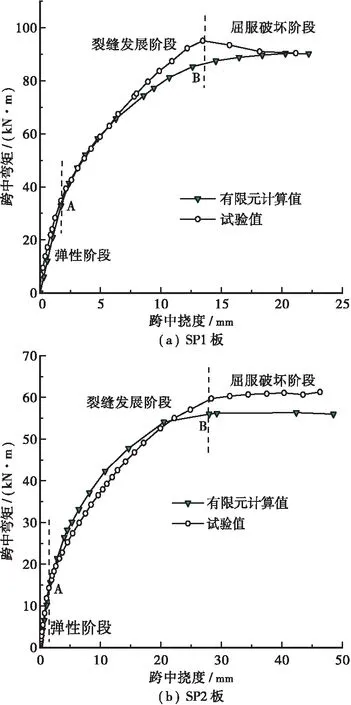
圖13 荷載-跨中撓度曲線對比Figure 13 Comparison of load-span deflection curves

表3 轉折點處彎矩對比分析結果Table 3 Comparative analysis of bending moments at turning points試件彎矩(A)/(kN·m)彎矩(B)/(kN·m)試驗值計算值相對誤差/%試驗值計算值相對誤差/%SP1板34.832.95.495.190.35.0SP2板14.315.69.161.356.28.3

3.4.2滑移分布曲線

圖14為試件開裂荷載時頂底板的滑移分布曲線對比圖，可以看出曲線吻合得較好。從有限元計算的結果可以看出，滑移沿著板的縱向嚴格對稱分布，跨中頂底板滑移為0，位于支座處的滑移量最大，與試驗測量結果保持一致。說明有限元模擬分析具有一定的可靠性。

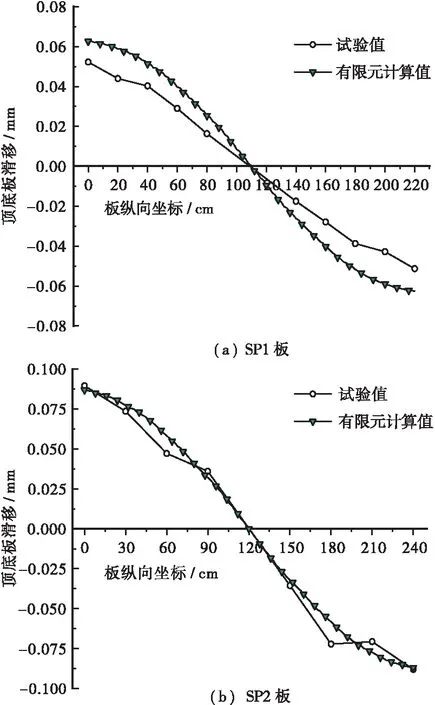
圖14 彈性階段頂底板滑移分布曲線Figure 14 Top-bottom slip distribution curve in elastic stage

3.4.3裂縫形態分布圖

圖15為各試件在達到極限承載力時的等效塑性應變圖，該圖可以很好地反映試件的裂縫形態以及對應的位置布置，從計算結果可以看出，試件SP1破壞時最終裂縫分布主要集中在底板跨中區域，試件SP2破壞時最終裂縫分布主要集中在頂板加載點處以及剪跨段底板短柱附近。對比試驗最終破壞形態圖9可以看出，二者在裂縫分布位置以及形態均吻合得較好。

(a)SP1板

4 參數分析

4.1 參數確定

在驗證了有限元模擬分析的可靠性以后，采用有限元對試件進行參數分析，從而進一步揭示帶鋼短柱UHPC夾芯板的力學性能。在試件SP1的基礎上，研究底板縱筋配筋率，頂底板的厚度、板的高度以及不銹鋼短柱的尺寸對試件抗彎性能的影響。具體參數見表4。

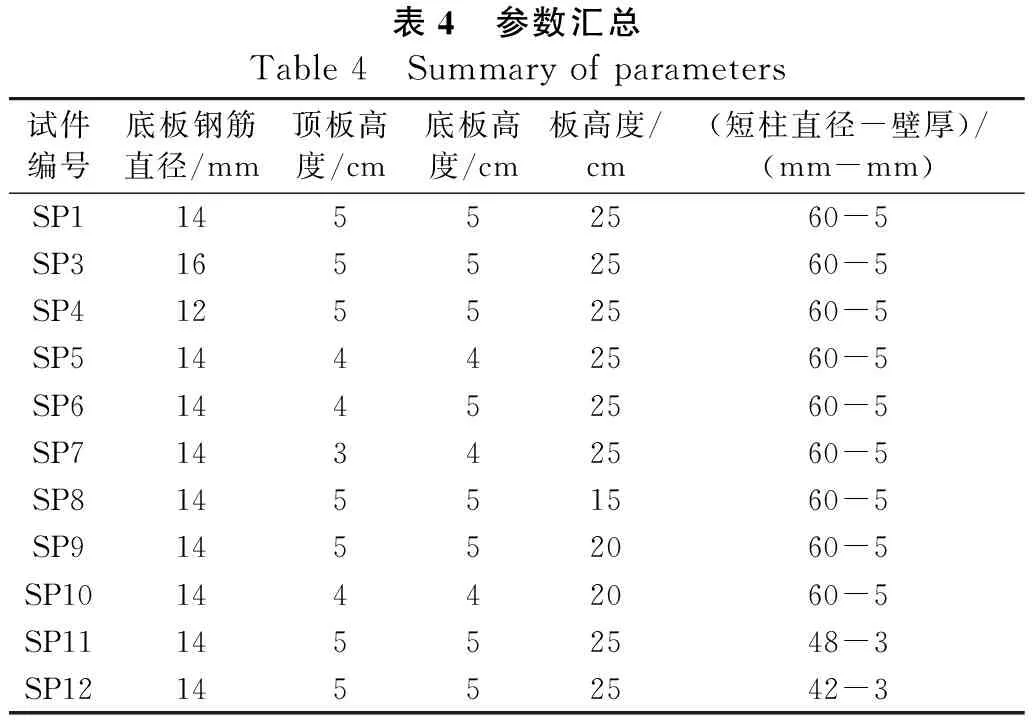
表4 參數匯總Table 4 Summary of parameters試件編號底板鋼筋直徑/mm頂板高度/cm底板高度/cm板高度/cm(短柱直徑-壁厚)/(mm-mm)SP114552560-5SP316552560-5SP412552560-5SP514442560-5SP614452560-5SP714342560-5SP814551560-5SP914552060-5SP1014442060-5SP1114552548-3SP1214552542-3

4.2 結果對比

根據有限元的計算，提取了每個分析結果中的荷載-跨中撓度曲線，為了便于與前文統一，這里的荷載仍然取對應板中的跨中彎矩。如圖16所示為每個試件的荷載-撓度曲線，模型中計算得到的開裂荷載以及極限荷載如表5所示。

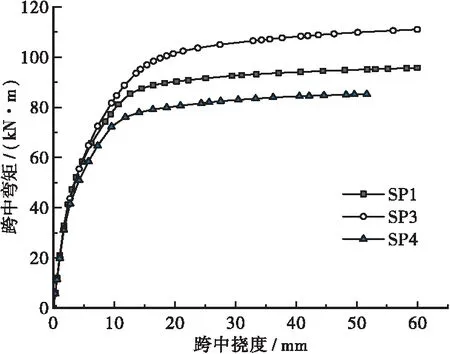
(a)不同配筋率

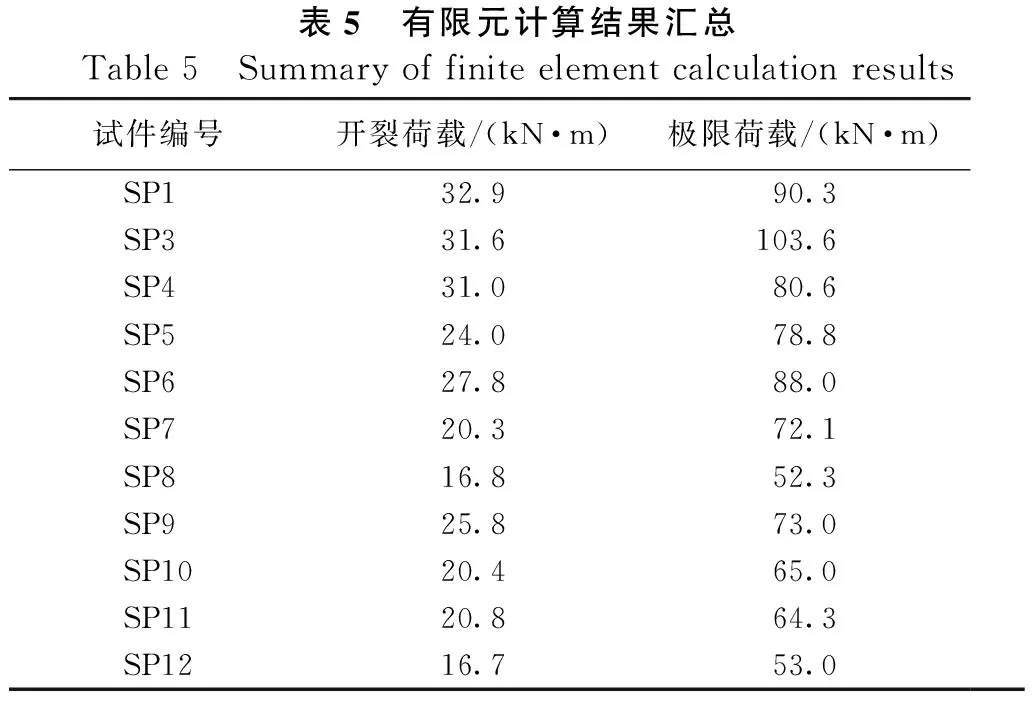
表5 有限元計算結果匯總Table 5 Summary of finite element calculation results試件編號開裂荷載/(kN·m)極限荷載/(kN·m)SP1 32.990.3SP3 31.6103.6SP4 31.080.6SP5 24.078.8SP6 27.888.0SP7 20.372.1SP8 16.852.3SP9 25.873.0SP1020.465.0SP1120.864.3SP1216.753.0

4.2.1配筋率

圖16(a)為不同配筋率模型的荷載-跨中撓度曲線，可以發現，當底板縱筋配筋率提高時，有限元模型開裂荷載幾乎保持不變，說明縱筋配筋的改變對板開裂前的抗彎性能影響較小；開裂以后板的剛度隨著配筋率的提高而提高，繼而板的極限承載力也有一定程度的提高。

4.2.2頂底板厚度

圖16(b)為不同頂底板厚度模型的荷載-跨中撓度曲線，可以看出，隨著頂底板厚度的增加，試件的開裂荷載以及極限荷載均有所增加，但增幅不盡相同，相較于頂板厚度，底板厚度對開裂荷載及極限荷載的影響更加顯著。板的高度越高，頂底板厚度的改變對開裂荷載及極限荷載影響越大。

4.2.3板高度

圖16(c)為不同板高模型的荷載-跨中撓度曲線，從中可以看出，板高度的變化對試件開裂荷載和極限荷載的影響是顯著的，隨著板的高度的降低，對應試件開裂荷載、極限荷載以及開裂后板的剛度均降幅明顯，且板高度越低，對應的降幅越明顯。

4.2.4短柱尺寸

圖16(d)為不同短柱模型的荷載-跨中撓度曲線，短柱的直徑減小時，試件對應的開裂荷載與極限荷載同樣下降明顯。與改變板高度不同的是，改變短柱直徑是通過改變頂底板抗滑移剛度間接影響板的抗彎剛度，從而影響板的抗彎性能。

綜上所述可以看出，板的高度和不銹鋼短柱的直徑是影響板受力性能最重要的因素，其次是頂底板的厚度和底板鋼筋的配筋率，其中頂底板厚度對板抗彎性能的影響程度與板的高度有關，當板的高度較低時，頂底板厚度的影響程度更加明顯；而底板鋼筋的配筋率對試件的開裂荷載影響不大，對試件開裂后的抗彎性能有一定影響。

5 結論

本文結合帶鋼短柱UHPC夾芯板抗彎性能試驗結果以及有限元軟件ABAQUS的模擬分析，得出了如下結論：

a.在荷載作用下UHPC夾芯板的破壞全過程可以分為3個階段，分別是線彈性階段、裂縫開展階段以及屈服破壞階段。

b.當板的高度相同時，短柱直徑越大越密集，試件的承載力、抗裂性能、剛度均顯著提升，試件的整體性能越強，其破壞形態更加接近普通混凝土板的受彎破壞；而短柱較稀疏時，試件的整體性能降低，短柱處的集中應力越明顯，裂縫分布較分散。

c.利用ABAQUS對試驗板進行了有限元模擬分析，有限元計算結果與試驗結果吻合較好。并對影響試件承載能力的相關參數進行有限元模型分析，總結了底板縱筋配筋率，頂底板的厚度、板的高度以及不銹鋼短柱對試件抗彎性能的影響規律，實際運用中，建議通過改變板的高度以及短柱的尺寸來合理提高板的抗裂性能和極限承載力。