基于改進蝗蟲算法的預應力曲線拐點識別研究

劉 珣， 虢曙安， 魏 維， 王祺順

( 湖南省交通科學研究院有限公司, 湖南 長沙 410015)

0 引言

預應力混凝土性能是大跨度混凝土箱梁橋承載力的主要影響因素之一。相比于傳統混凝土結構，預應力混凝土可以充分發揮鋼筋的承載能力，有效提高結構構件的抗裂性能和整體剛度，延長結構耐久性。預應力混凝土主要通過對預應力鋼筋進行張拉，使鋼筋產生一定的形變來抵消結構本身產生的荷載，因此，預應力張拉質量的控制是預應力混凝土箱梁橋承載能力的重要保障，各專家學者也在此領域展開了深入的研究。周宏宇[1]等基于基頻法模擬了預應力混凝土箱梁疲勞剛度的規劃規律，驗證了預應力梁體“先快速、后平穩”的兩階段疲勞剛度退化模型；杜孟林[2]等對預應力混凝土空心板梁的抗剪承載力展開研究，通過數值模擬和試驗對比的方式證明了預應力損失對結構抗剪極限承載力影響有限的結論；孫亞林[3]等使用有限元軟件對大跨度連續剛構橋施工階段預應力損失進行研究，并發現可以通過合理計算張拉長度來減少預應力損失；蔣慶[4]等根據鋼絞線張拉后的衰退效應，揭示了后張法預應力損失呈對數函數增長，且實測值比數值模擬值更大；鄒國慶[5]等采用優化算法對預應力二次張拉曲線的拐點進行尋優識別，得到了改進遺傳算法對預應力曲線拐點識別精度更高的結論。

本文以經過預應力二次張拉的預制梁為研究對象，通過改進一種新型群智能優化算法——蝗蟲優化算法，對預應力二次張拉曲線進行尋優擬合，為預應力二次張拉曲線的擬合和拐點識別提供一種高效的研究方式。

1 預應力二次張拉理論

1.1 預應力二次張拉原理

“預應力二次張拉法”也稱“反拉法”，是指對錨索進行首次預應力張拉鎖定后，對錨索實施二次張拉鎖定的過程。如圖1所示，將預應力鋼索A端固定，對另一端施加張拉控制應力F0，待鋼索伸張，預留出二次張拉長度d2后通過夾持裝置對張拉端進行固定，此時設AB段鋼索彈性系數為k1，完成一次張拉。

對鋼索進行二次張拉時，如張拉控制應力FF0，設鋼索二次張拉預留長度為d2，彈性系數為k2，鋼索最大張拉長度對應的張拉控制應力為Fmax，鋼索AC全段同時受到二次張拉控制應力作用，根據胡克定律的串聯型線彈性模型，二次張拉的F-x函數如式(1)所示:

(1)

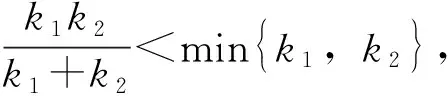
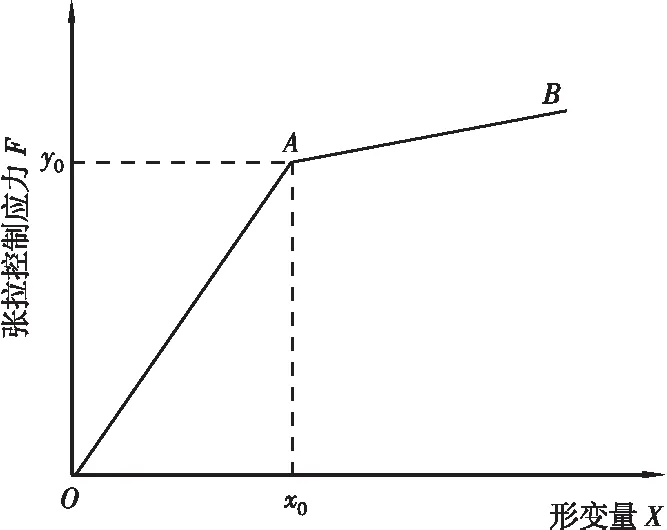
圖2 預應力二次張拉曲線Figure 2 Prestressed secondary tension curve

1.2 預應力二次張拉曲線拐點尋優模型

由預應力二次張拉的過程和原理可知，當兩條直線上的點與預應力張拉實測值的誤差在一定范圍內時，兩直線的交點即為預應力二次張拉曲線的拐點，基于此，可以將預應力二次張拉拐點識別的求解問題轉化為對兩直線軌跡點與預應力張拉實測值間最小誤差的優化求解問題。

1.2.1目標函數的確定

設兩直線方程分別為y1=k1x+b1;y2=k2x+b2，拐點A坐標為(x0，y0)，張拉控制應力與伸長量的實測數據N={F，S}={(f1，s1)，(f2，s2)…(fn，sn)}，其中fi(i=1，2…n)為張拉控制應力數據樣本；si(i=1，2…n)為對應伸長量數據樣本。則兩直線間的數據離散型函數如式(2)所示:

(2)

選取數值擬合的離散性結果與實測結果之間的誤差為目標函數，則當目標函數取最小值時，該情形下的點p(xi，yi)即為優化問題的最優解。目標函數如式(3)所示:

(3)

1.2.2優化參數的確定

選取預應力二次張拉曲線模型中的k1，k2，b1，b2，p(x0，y0)這5個參數為目標優化參數，首先確定優化參數的可能取值范圍。確定參數取值范圍中心點的步驟如下[6]：

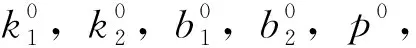
b.遍歷式搜尋：對實測數據集N進行遍歷式搜尋，并記當前數據點為ni(fi，si)；

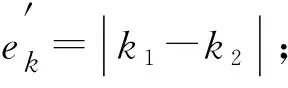
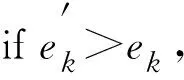
e.如對數據集N完成遍歷，轉步驟f，否則轉步驟b；

f.確定參數取值中心。

2 基于改進蝗蟲算法的尋優模型

2.1 蝗蟲優化算法

蝗蟲優化算法(GOA)是一種元啟式仿生優化算法，其原理是根據蝗蟲成蟲大規模搜索和幼蟲小范圍移動的覓食規律，使種群整體向食物源靠近，實現種群整體的位置優化。蝗蟲優化算法中，蝗蟲個體映射為在空間內部搜索的點，蝗蟲間的相互作用用函數模擬，蝗蟲尋找食物源過程即為算法尋優過程，蝗蟲位置的更新為優化過程中的迭代和最優解選取，將蝗蟲在D維空間中的種群遷移和覓食行為模擬為數學模型，令Xi為蝗蟲在空間中的位置；Si為蝗蟲個體間的相互作用；Gi為蝗蟲受到的重力作用；Ai為蝗蟲受到的風力作用，則GOA的基本數學模型如式(4)所示：

Xi=Si+Gi+Ai

(4)

其中，蝗蟲個體受到的各類作用如式(5)～式(7)：

(5)

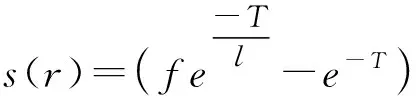
Gi=-geg

(6)

式中：g為重力加速度；eg為指向地心的單位向量。

Ai=uew

(7)

式中：u為風力常量；ew為指向風向的單位向量。

為了適應優化問題的求解，排除蝗蟲種群到達舒適區后種群未收斂的問題，忽略重力影響并假定風向始終指向最優解，通過引入遞減系數c減少蝗蟲間的相互作用來改進GOA數學模型，遞減系數c影響蟲群舒適區、引力區和斥力區的大小，計算方法如式(8)所示：

c=cmax-n(cmax-cmin)/L

(8)

式中：n為當前迭代次數；L為最大迭代次數。適應優化問題的GOA數學模型如式(9)所示：

(9)

式中：us和ls為函數s(r)在D維空間上的上下界；Td為當前蝗蟲位置的最優解。

2.2 基于柯西算子改進的GOA算法

2.2.1服從均勻分布的調整策略

根據式(9)可知，GOA數學模型中遞減系數c是蟲群探索和開發的關鍵控制參數，由于參數c隨迭代次數動態變化，前期下降過快會導致蟲群的全局搜索能力受限，后期下降過慢會導致蟲群局部收斂速度放緩，根據均勻分布隨機調整策略[7]，重新構建遞減系數c(n)如式(10)所示：

c(n)=

(10)

式中：δ為服從[0，L]均勻分布的隨機數，且δ∈[0，1]。

2.2.2引入柯西算子的更新策略

根據服從均勻分布調整策略后的GOA特性，將算法分為前后兩部分分別進行改進。受到粒子群優化算法記憶策略的啟發，對服從均勻分布的蝗蟲算法進一步改進，如式(11)所示，在算法搜索前半段對每代最優解記憶并保存。

Xi(n+1)(n+1)=b1Xi+

b2r1[Xbest(n)-Xi(n)]+

b2r2[Xj(n)-Xk(n)]

(11)

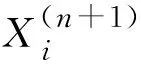
由式(9)可知，GOA算法中蝗蟲位置更新取決于自身位置和與周邊蝗蟲的相互作用，因此GOA擁有較強的局部開發能力，但全局探索能力較弱。為避免算法陷入局部最優的情形，在算法后半段引入柯西算子變異計算步長，幫助個體跳出局部極值點，加強全局尋優能力。引入柯西算子后的改進GOA模型如式(12)所示：

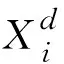
(12)

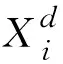
(13)

混合均勻分布和柯西改進后的蝗蟲優化算法(CUGOA)在保證前期全局開發能力的基礎上，幫助個體逃離局部舒適區，防止陷入局部最優，理論上可以達到更高的收斂精度和收斂速度。

2.2.3CUGOA優化策略

根據優化問題的求解思想，在CUGOA算法的前半段，需要側重算法的全局搜索能力，定位相對舒適區；在算法后期，通過引入柯西算子降低了算法陷入局部最優解的概率，并在一定程度上加快了CUGOA的收斂速度，判斷算法進行全局搜索和局部開發由控制概率Pc決定：

(14)

具體的位置更新策略如下，

算法1：結合均勻分布和柯西算子的改進策略。

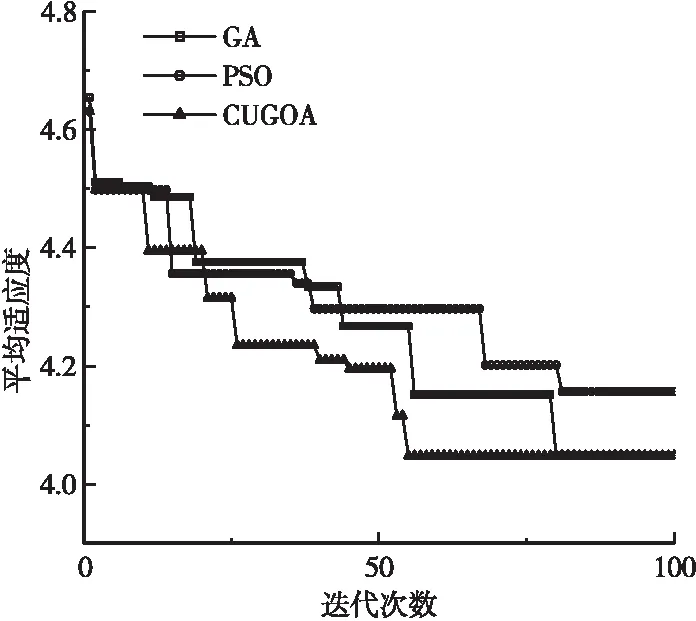
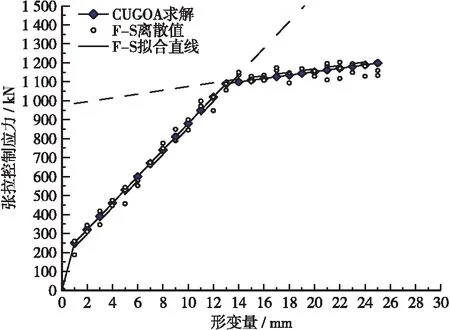
a.ifrand

b.根據式(9)更新蝗蟲位置；

c.else,

d.根據式(12)更新蝗蟲位置；

e.end。

2.2.4算法性能對比

為驗證改進后的算法性能，采用Rastrigin函數對算法進行測試，參與測試的算法有：蝗蟲算法(GOA)、服從均勻分布的蝗蟲算法(GOA1)、引入柯西算子的蝗蟲算法(GOA2)、混合均勻分布和柯西算子改進的蝗蟲算法(CUGOA)。測試函數表達式如式(15)所示，函數理論值為0，測試結果如表1所示。

表1 Rastrigin函數算法性能測試結果Table1 Rastrigin function algorithm performance test results算法名最優值最差值均值標準差耗時/sGOA9.64E+011.67E+021.35E+022.05E+0155.64GOA10.00E+001.89E+011.25E+011.43E+0141.37GOA20.00E+001.73E+011.14E+011.36E+0135.46CUGOA0.00E+000.00E+000.00E+000.00E+0025.76

xi∈[-5.12， 5.12]

(15)

由標準蝗蟲算法和3種不同程度改進的蝗蟲算法在Rastrigin測試函數下的平均收斂結果可知，傳統GOA算法在尋優過程中極易陷入函數局部極值而尋優失敗，服從均勻分布的GOA1可以尋找到函數最小值，但收斂速度不如引入柯西算子的GOA2快，而同時引入2種改進策略的CUGOA能夠在準確收斂到最優解的前提下保持較高的收斂效率，證明混合均勻分布和柯西算子改進后的蝗蟲算法性能更強。

2.3 基于CUGOA的預應力拐點識別模型

本文基于GOA算法改進，提出服從均勻分布和引入柯西算子的CUGOA算法，并將其應用于預應力二次張拉曲線的拐點識別中，預測模型算法執行流程如圖3所示。執行步驟如下:

圖3 基于CUGOA的預應力拐點識別模型Figure 3 Recognition model of prestress inflection point based on CUGOA

a.確定優化參數：確定優化參數的個數，調整蝗蟲個體維度與優化參數個數保持一致；

b.數據預處理：對預應力二次張拉曲線模型中的k1，k2，b1，b2，p(x0，y0)這5個參數進行預處理，確定參數取值中心；

c.初始化CUGOA參數：初始化種群大小、空間維度、最大迭代次數等基本參數；

d.初始化種群位置：初始化蝗蟲種群位置，并計算種群適應度值；

e.更新遞減系數：按服從均勻分布的改進策略更新遞減系數c(n)；

f.計算控制概率Pc并執行算法1：判斷算法執行全局搜索或局部開發；

g.更新目標位置：重新計算種群適應度，通過比對記憶中的最優位置更新當前目標位置；

h.停止條件：滿足停止條件則終止算法輸出種群最優值，否則返回步驟e。

3 尋優結果分析

根據平益高速公路項目現場對模型梁進行的試驗，共計對500根預應力鋼絞線進行預應力二次張拉，獲取預應力張拉數據共計2 000余組，對張拉數據進行初篩處理后，使用遺傳算法(GA)、粒子群算法(PSO)和改進的蝗蟲算法(CUGOA)共3種典型優化算法對處理后的樣本數據進行適應度計算，各算法計算出的平均適應度收斂曲線如圖4所示。

圖4 典型算法平均適應度曲線Figure 4 Average fitness curve of typical algorithms

由圖4可知，GA和CUGOA算法均能在最大迭代周期內達到最佳收斂，但CUGOA對預應力二次張拉數據的敏感程度更高，收斂速度更快，跳出局部極值能力最強。PSO雖然前期能以較快的速度將優化參數定位到拐點附近，但后期算法性能下降較快，對預應力張拉曲線拐點的精確識別能力較差，綜合來看，CUGOA算法性能更強。

圖5給出了CUGOA的尋優結果、處理過的多組實測數據離散點和離散值擬合直線，由圖5可知，CUGOA對實測數據的擬合度較高，可以達到對預應力張拉控制應力離散值的基本吻合，對兩直線模型參數的優化較為準確，識別出的拐點偏離程度較小，接近真實值。

圖5 CUGOA預應力曲線拐點識別Figure 5 Recognition of inflection point of CUGOA prestress curve

(16)

通過式(16)計算GA和CUGOA預應力二次張拉曲線拐點尋優模型的擬合標準差，可知RMSE=0.18<1，說明CUGOA可快速精確定位預應力二次張拉曲線拐點，且誤差控制良好。

4 結論

本文基于混合均勻分布和柯西算子改進的蝗蟲優化算法，對預應力二次張拉曲線拐點識別問題建立數學尋優模型并進行求解，得到的結論如下：

a.預應力二次張拉曲線拐點識別的問題可以轉化為以數值擬合和實測數據間誤差最小值為目標函數的優化問題。

b.相較于標準蝗蟲算法或單一策略改進的蝗蟲算法，混合策略改進后的蝗蟲算法性能提升明顯，在兼顧全局搜索與局部開發能力的前提下仍能保持最快的收斂速度。

c.混合均勻分布和柯西算子改進的蝗蟲優化算法對預應力曲線拐點求解的問題具有良好的適應性，其尋優精度和收斂速度均超過傳統遺傳算法和粒子群算法。