基于導軌多激勵關聯(lián)的轎廂水平振動預測方法*

武 儀,薩日娜,,*,裘樂淼,張利春,張 靜

(1.內(nèi)蒙古工業(yè)大學 機械工程學院,內(nèi)蒙古 呼和浩特 010051;2.浙江大學 機械工程學院,浙江 杭州 310027;3.康力電梯股份有限公司,江蘇 蘇州 215213)

0 引 言

高速電梯是高層建筑必不可少的運輸設備。高速電梯的振動性能是決定電梯安全性和舒適性的關鍵因素。如何在設計階段有效預測高速電梯的振動特性,對提高電梯產(chǎn)品設計方案穩(wěn)健性具有重要意義。

國內(nèi)外研究學者針對電梯振動預測問題進行了大量研究。這些研究主要包括振動建模、振動仿真、預測算法3個方面:

(1)振動建模方面。QIU L M等人[1]2-4提出了轎廂設計參數(shù)優(yōu)化方法,建立了轎廂水平振動的二自由度動力學方程。ZHANG R J等人[2]考慮滾動導靴的非線性特性,建立了滾動導靴的非線性模型。LIU J等人[3]考慮氣流和導向系統(tǒng)共同作用,建立了轎廂的水平振動動力學模型。WANG C等人[4]考慮了參數(shù)隨機性,根據(jù)攝動理論分析了轎廂觀測點的橫向振動加速度響應。

(2)振動仿真方面。KAZUKI S等人[5]提出了一種導靴仿真模型,用以評估由導靴所產(chǎn)生的應力引起的電梯橫向振動;并且將仿真結(jié)果應用于導軌結(jié)構(gòu)參數(shù)的設計中。QIU L M[1]5、陳杰等人[6，7]研究了彎曲激勵單獨作用對轎廂水平振動的影響。郭天水[8]研究了彎曲激勵、階躍激勵和失調(diào)激勵疊加情況下,轎廂水平振動的響應。

(3)預測算法方面。主要研究成果有擬合方法和機器學習方法[9-18]。其中,擬合方法包括多項式擬合、最小二乘擬合、響應面擬合等;機器學習方法包括人工神經(jīng)網(wǎng)絡、支持向量機回歸等。

以上研究對電梯振動預測研究具有重要參考價值。現(xiàn)有對轎廂水平振動的研究主要考慮的是導軌單因素激勵[19-24]。然而引起高速電梯轎廂水平振動的激勵因素有很多。導軌是電梯導向系統(tǒng)的重要部件。由于制造、安裝誤差等原因,導軌會存在彎曲、階躍、失調(diào)等問題。這些因素之間的相互關聯(lián)作用,也影響著轎廂的水平振動。例如導軌彎曲變形會引起導軌拼接處傾斜,進而導致導軌失調(diào)。導軌拼接處錯位會導致導靴滾輪跳動,進而使導軌的受力不均勻,而且轎廂長時間在變載荷作用下運行,會導致導軌局部彎曲變形、表面磨損等問題的發(fā)生。

針對以上問題,筆者結(jié)合導靴-導軌接觸模型,建立高速電梯轎廂二自由度水平振動等效動力學模型,考慮導軌多源激勵關聯(lián)性,并基于Dematel方法得出各激勵的重要度;構(gòu)建基于布谷鳥算法改進的支持向量機回歸方法,建立轎廂水平振動預測模型,對比分析CS-SVR、SVR、RBF、BP、GA-BP預測結(jié)果,最后通過康力KLK2電梯樣機進行對比實驗。

1 轎廂水平振動模型

1.1 導靴-導軌接觸模型

電梯導靴分為滑動導靴和滾動導靴。滑動導靴主要用于低速電梯,而滾動導靴主要用于高速和超高速電梯。導靴主要由滾輪、搖臂、彈簧、限位裝置和靴座組成;滾輪主要由金屬或尼龍材質(zhì)的輪轂和外圈硬質(zhì)橡膠組成,其彈性元件主要為彈簧和滾輪外圈橡膠。

由機械動力學理論可知,質(zhì)量彈性元件同時具有慣性、彈性和阻尼3種特性,而相對于轎廂系統(tǒng)的質(zhì)量,導靴的質(zhì)量非常小,為了便于分析,此處忽略導靴的質(zhì)量。由于滾輪橡膠的剛度遠大于彈簧的剛度,工作時導輪橡膠形變較小,筆者在研究和建模中將其視為剛體,不考慮導輪和導軌間的彈性接觸關系;將導靴簡化為彈簧阻尼系統(tǒng),建立導靴-導軌接觸振動模型。

1.2 轎廂水平振動建模

在進行轎廂水平振動分析之前,需要建立轎廂振動坐標系。筆者以轎廂質(zhì)心為原點,以平行于轎廂門運動方向為X軸,以平行于轎廂側(cè)向為Y軸,以轎廂提升方向為Z軸,建立空間直角坐標系。

轎廂振動坐標系如圖1所示。

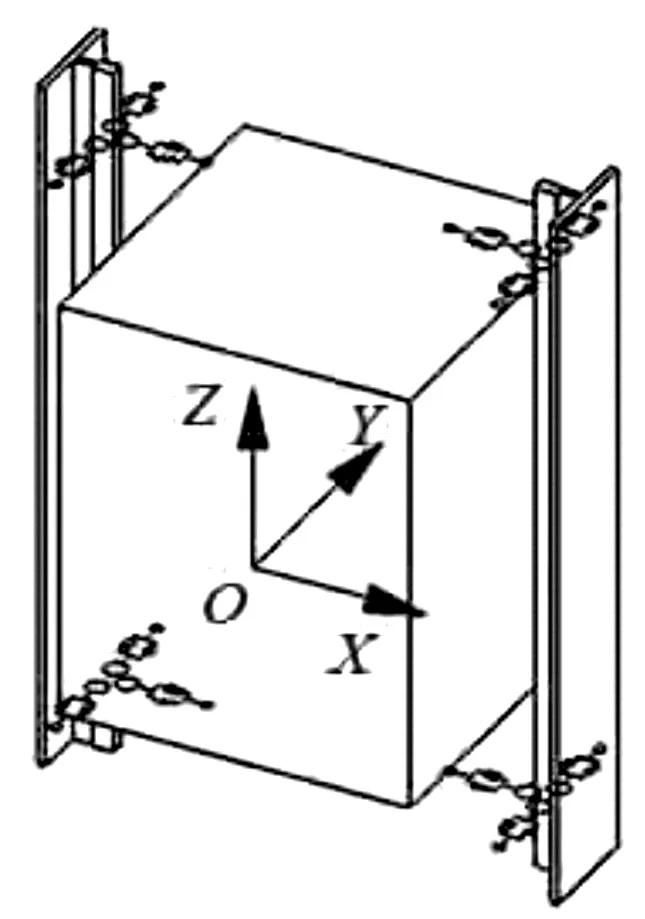
圖1 轎廂振動坐標系

按空間維度劃分,電梯振動通常分為橫、縱、側(cè)3個方向。圖1中,橫向振動對應平行于X軸方向的移動和繞著Y軸的轉(zhuǎn)動,側(cè)向振動對應平行于Y軸方向的移動和繞著X軸的轉(zhuǎn)動,縱向振動對應平行于Z軸方向的移動。此處,筆者主要研究的是由于導軌多源激勵作用下引起的轎廂橫向振動。

而實際上,電梯是非常復雜的機電一體化設備,影響電梯振動的因素也非常復雜。為了便于分析計算,此處做出3項假設:(1)將轎廂和轎廂架視為整體,忽略細節(jié)影響;(2)將4只導靴視為彈簧阻尼系統(tǒng),且4只導靴的等效剛度及等效阻尼均相等;(3)忽略滾輪橡膠變形對轎廂振動的影響[1]4。

轎廂二自由度水平振動等效動力學模型如圖2所示。

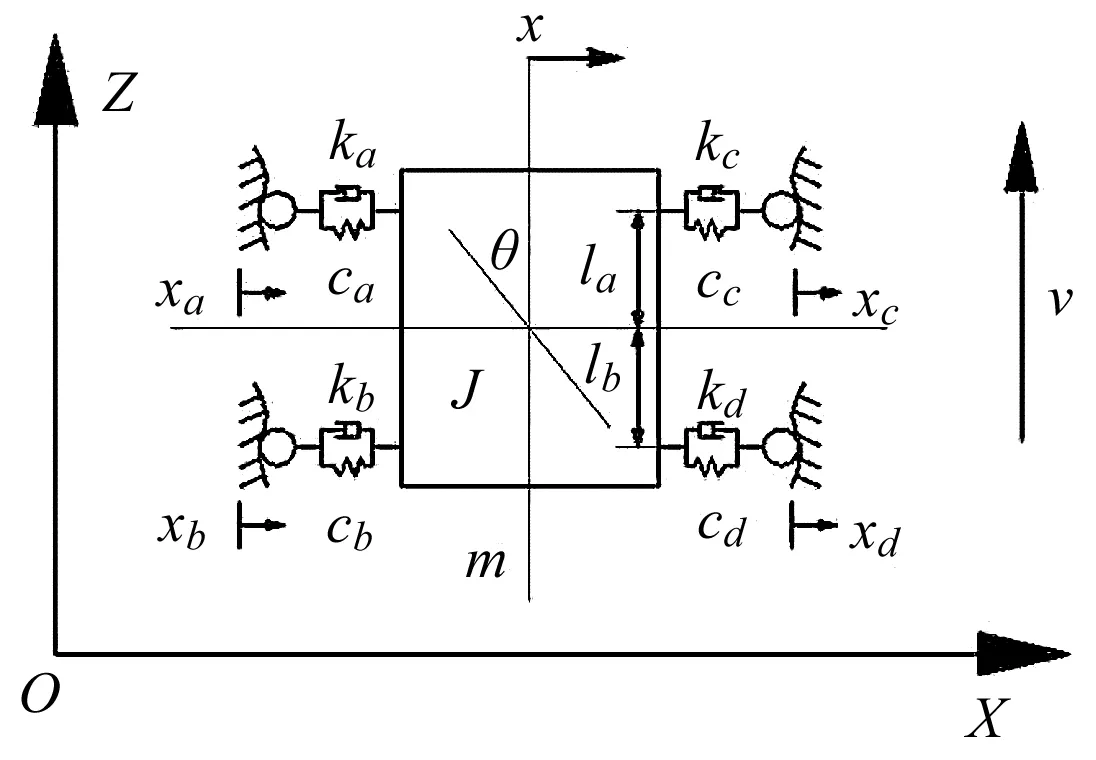
圖2 轎廂二自由度水平振動等效動力學模型x—轎廂水平振動位移(以向右為正方向);θ—轎廂繞其質(zhì)心轉(zhuǎn)動的角位移(以逆時針為正方向);xa,xb,xc,xd—4只導靴的位移激勵(以向右為正方向);v—電梯運行速度;m—轎廂及轎廂架的質(zhì)量;J—轎廂及轎廂架的轉(zhuǎn)動慣量;ka,kb,kc,kd—4只導靴的等效剛度;ca,cb,cc,cd—4只導靴的等效阻尼;la—導靴a和c到轎廂質(zhì)心的垂直距離;lb—導靴b和d到轎廂質(zhì)心的垂直距離

下面對動力學模型進行分析。根據(jù)牛頓第二定律,電梯轎廂水平振動的動力學方程為:

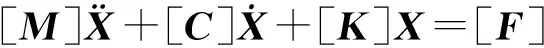
(1)

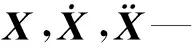
根據(jù)牛頓第二定律、振動基本原理、彈性元件和阻尼元件的動力學特性,可得到高速電梯水平振動動力學系統(tǒng)微分方程:

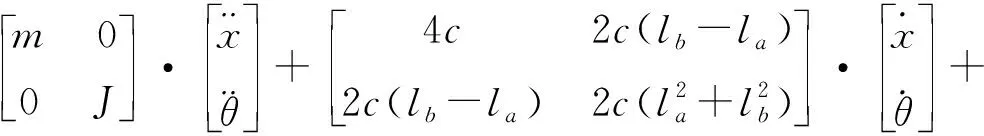
(2)

2 導軌多源激勵關聯(lián)性分析

2.1 導軌多源激勵因素分析

電梯導向系統(tǒng)的核心部件是導軌和導靴,其主要功能是限制轎廂與對重的運動自由度,使轎廂與對重只能沿著導軌鉛垂線作升降運動。導軌本身的安裝缺陷,如導軌對中誤差、導軌垂直度誤差、導軌接頭不夠平整、軌距在全高上誤差過大、導軌支架松動、導軌表面粗糙不平和導輪缺陷等,均可能引起轎廂運行過程中產(chǎn)生水平振動。

綜合考慮各種因素,筆者將導軌激勵抽象為3種典型的激勵因素:失調(diào)激勵、彎曲激勵和階躍激勵。

導軌多源激勵因素分析結(jié)果如表1所示。

表1 導軌多源激勵因素分析結(jié)果

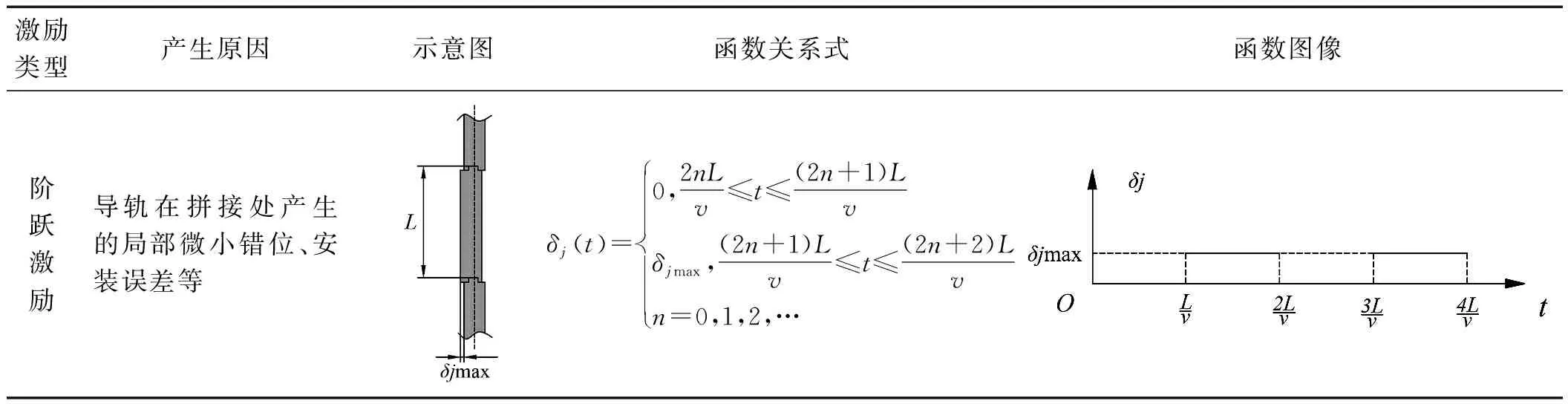
續(xù)表

2.2 導軌多源激勵采樣

首先,筆者進行單獨激勵下的振動仿真,分析每種激勵單獨作用下轎廂水平振動響應;然后,考慮所有激勵關聯(lián)性,進行總體仿真分析。此處以電梯經(jīng)過8根導軌的時間作為仿真總時長,單根導軌長為5 m,電梯運行速度為4 m/s,仿真總時長為10 s。由于左右兩根導軌對導靴的激勵程度完全一致,導靴a、c的激勵信號相同,導靴b、d的激勵信號相同;上、下兩導靴間距為2.2 m,通過計算可以得出同側(cè)導靴激勵之間的時間間隔為0.55 s。

激勵輸入圖像如圖3所示。

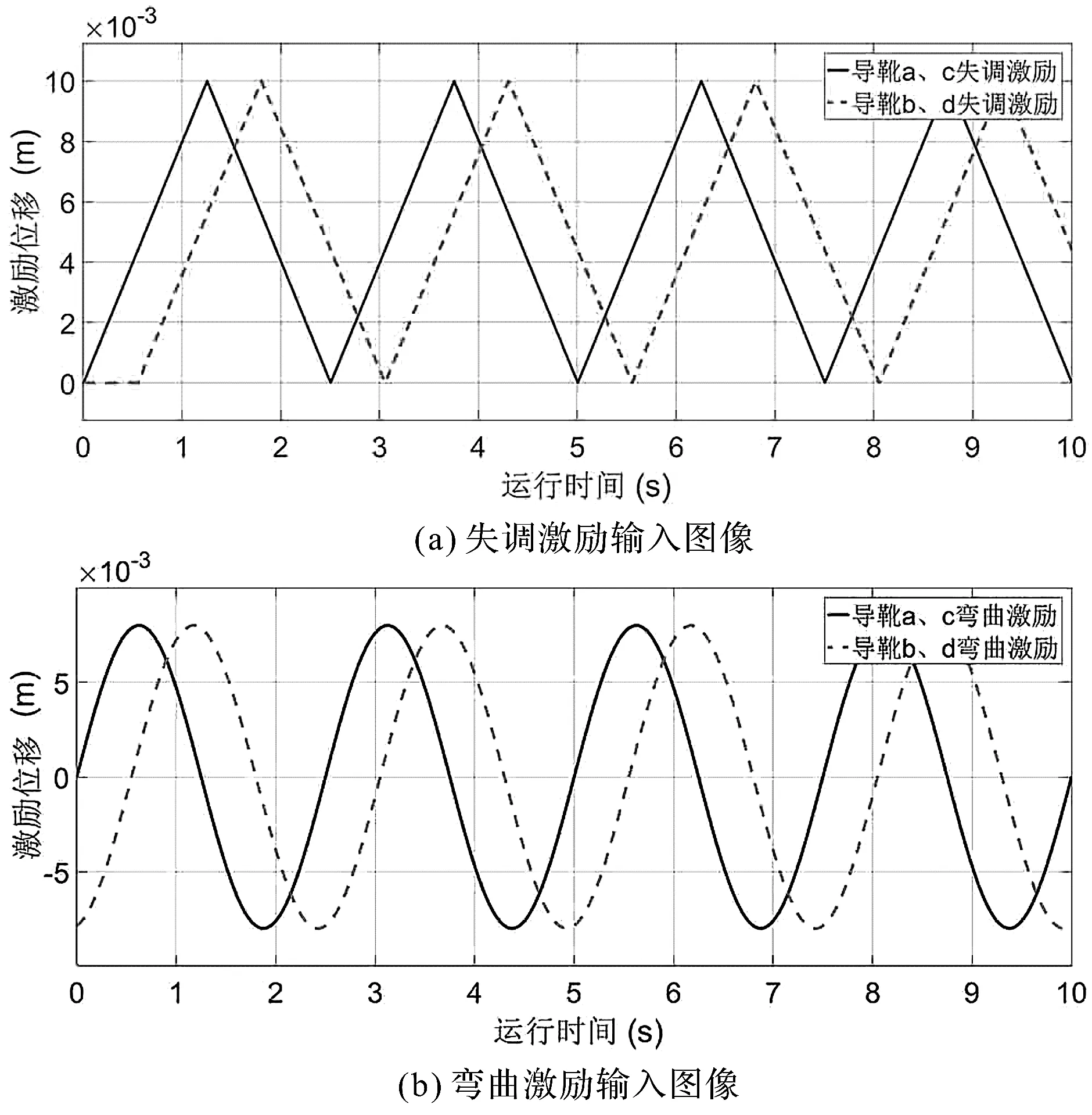
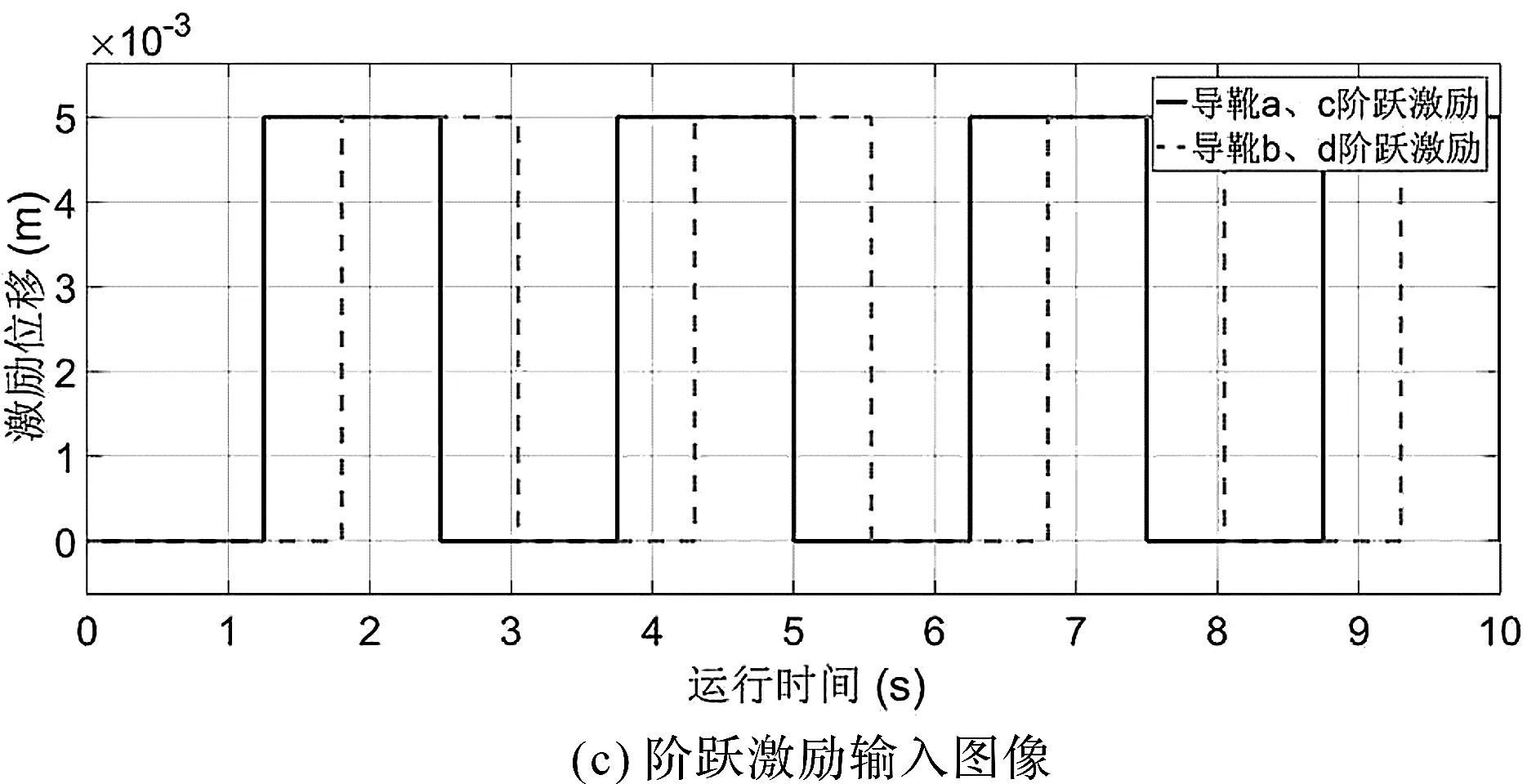
圖3 激勵輸入圖像

筆者以導靴a、c為標準,計算各激勵直接影響矩陣,將上述導軌各激勵輸入進行離散化,分別取每種激勵1 s～9 s的9個時刻位移絕對值,組成直接影響矩陣。例如,失調(diào)激勵1 s、2 s、3 s的3個時刻激勵位移分別為0.008 m、0.004 m、0.004 m,作為失調(diào)激勵直接影響矩陣B1的第1行;4 s、5 s、6 s的3個時刻激勵位移分別為0.008 m、0 m、0.008 m,作為失調(diào)激勵直接影響矩陣B1的第2行;7 s、8 s、9 s的3個時刻激勵位移分別為0.004 m、0.004 m、0.008 m,作為失調(diào)激勵直接影響矩陣B1的第3行。彎曲激勵和階躍激勵同理。

最后，為了便于計算,筆者將各數(shù)值整體擴大1 000倍,得到各激勵直接影響矩陣Bk(k=1,2,3):

(3)

(4)

(5)

式中:B1—失調(diào)激勵直接影響矩陣;B2—彎曲激勵直接影響矩陣;B3—階躍激勵直接影響矩陣。

2.3 導軌多源激勵關聯(lián)性分析

Dematel方法是運用圖論與矩陣工具進行系統(tǒng)要素分析的方法,是分析特征關聯(lián)性的有效工具。采用Dematel方法計算各激勵重要度過程如下:

(1)將各激勵數(shù)據(jù)離散化,得到各個激勵直接影響矩陣Bk=(bij)n×n,(k=1,2,3)。

(2)將直接影響矩陣Bk做歸一化處理,得到矩陣Mk(k=1,2,3):

(6)

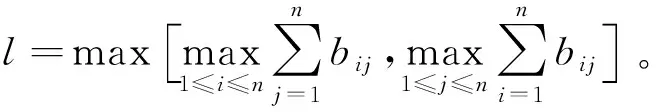
(3)計算出綜合影響矩陣Xk(k=1,2,3):

Xk=(xij)n×n=Mk(I-Mk)-1

(7)

式中:(I-Mk)-1—矩陣(I-Mk)的逆矩陣;I—單位矩陣。

(4)根據(jù)綜合影響矩陣,計算出各個屬性的中心度a以及原因度b:

(8)

(5)確定各激勵的重要度:

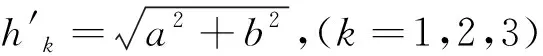
(9)

式中:h1—失調(diào)激勵重要度;h2—彎曲激勵重要度;h3—階躍激勵重要度。

3 CS-SVR轎廂水平振動預測

3.1 水平振動預測模型

雖然采用SVR方法進行非線性函數(shù)擬合的效果很好,但是需要調(diào)節(jié)懲罰因子C和RBF核參數(shù)γ,才能得到較好的精度。傳統(tǒng)SVR模型采用網(wǎng)格遍歷和交叉驗證的方法,對參數(shù)C和γ進行尋優(yōu)搜索。由于網(wǎng)格遍歷方法尋優(yōu)速度慢且效率低,當參數(shù)范圍較大時,無法保證尋優(yōu)速度和精度。基于此,筆者采用布谷鳥算法改進支持向量機回歸。

CS-SVR振動預測模型如圖4所示。

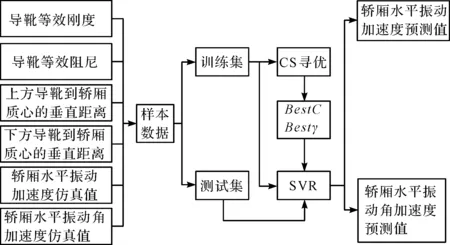
圖4 CS-SVR振動預測模型

3.2 CS-SVR模型預測步驟

布谷鳥搜索算法具有隨機搜索路徑優(yōu)和尋優(yōu)能力強的特點[25],采用CS算法優(yōu)化SVR參數(shù)尋優(yōu)過程,可以有效避免過擬合和欠擬合狀態(tài)的發(fā)生,并且提高尋優(yōu)效率。

CS-SVR模型預測步驟如下所示:

(1)仿真得到轎廂水平振動響應樣本數(shù)據(jù),進行歸一化處理,劃分訓練集和測試集;

(2)設定參數(shù)C和γ的取值范圍為0.01～100,設定CS算法的迭代次數(shù)為50次,鳥巢個數(shù)為20個,設定概率Pa=0.25;

(3)隨機產(chǎn)生20個鳥巢并初始化,以當前鳥巢對應的參數(shù)C和γ訓練SVR模型,計算SVR平均均方誤差,找到目前最優(yōu)的鳥巢位置,即最低的平均均方誤差;

(4)保留上一代最優(yōu)鳥巢位置,并進行Levy飛行更新一組鳥巢位置,使用新的C和γ參數(shù)值訓練SVR模型,計算每個鳥巢的平均均方誤差;

(5)判斷新鳥巢的平均均方誤差是否低于舊鳥巢的平均均方誤差,若不低于,則保留舊鳥巢;若低于,則使用新鳥巢代替舊鳥巢,得到一組較優(yōu)的鳥巢位置;

(6)使用隨機數(shù)r與Pa進行比較,判斷是否需要更新鳥巢位置。如果r>Pa,則保留上一代中被發(fā)現(xiàn)概率較小的鳥巢,并對被發(fā)現(xiàn)概率較大的鳥巢進行位置更新,計算新鳥巢的平均均方誤差,并且與舊鳥巢的平均均方誤差進行比較,用較優(yōu)的鳥巢位置代替差的位置,得到一組最優(yōu)的鳥巢位置;如果r≤Pa,則保留上一代鳥巢位置;

(7)判斷算法是否達到迭代次數(shù),若未達到,則返回步驟(4)繼續(xù)尋優(yōu)搜索;若達到,則停止搜索,并輸出全局最低平均均方誤差對應的最優(yōu)鳥巢;

(8)提取最優(yōu)鳥巢所對應的最優(yōu)參數(shù)C和γ,設置為SVR模型參數(shù);

(9)使用訓練集數(shù)據(jù)對SVR模型進行訓練;

(10)使用測試集數(shù)據(jù)對SVR模型進行測試,將數(shù)據(jù)反歸一化,計算出模型一系列的評價指標值。

高速電梯水平振動預測總流程如圖5所示。

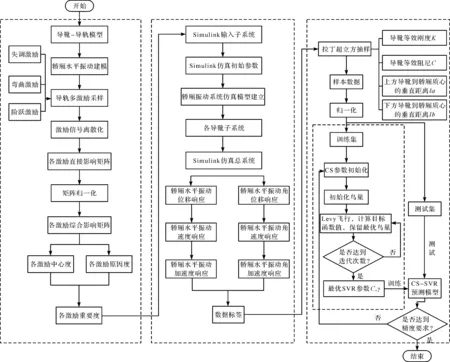
圖5 高速電梯水平振動預測總流程

4 實驗驗證

4.1 轎廂水平振動特性仿真分析

筆者采用康力KLK2型高速電梯進行實驗驗證。KLK2型高速電梯主要參數(shù)如表2所示。

表2 KLK2型高速電梯主要參數(shù)

4.1.1 單因素激勵作用下轎廂水平振動位移響應分析

為了便于對比分析,筆者將各激勵單獨作用下轎廂水平振動響應繪制在一張圖中。各激勵單獨作用下轎廂水平振動位移響應如圖6所示。

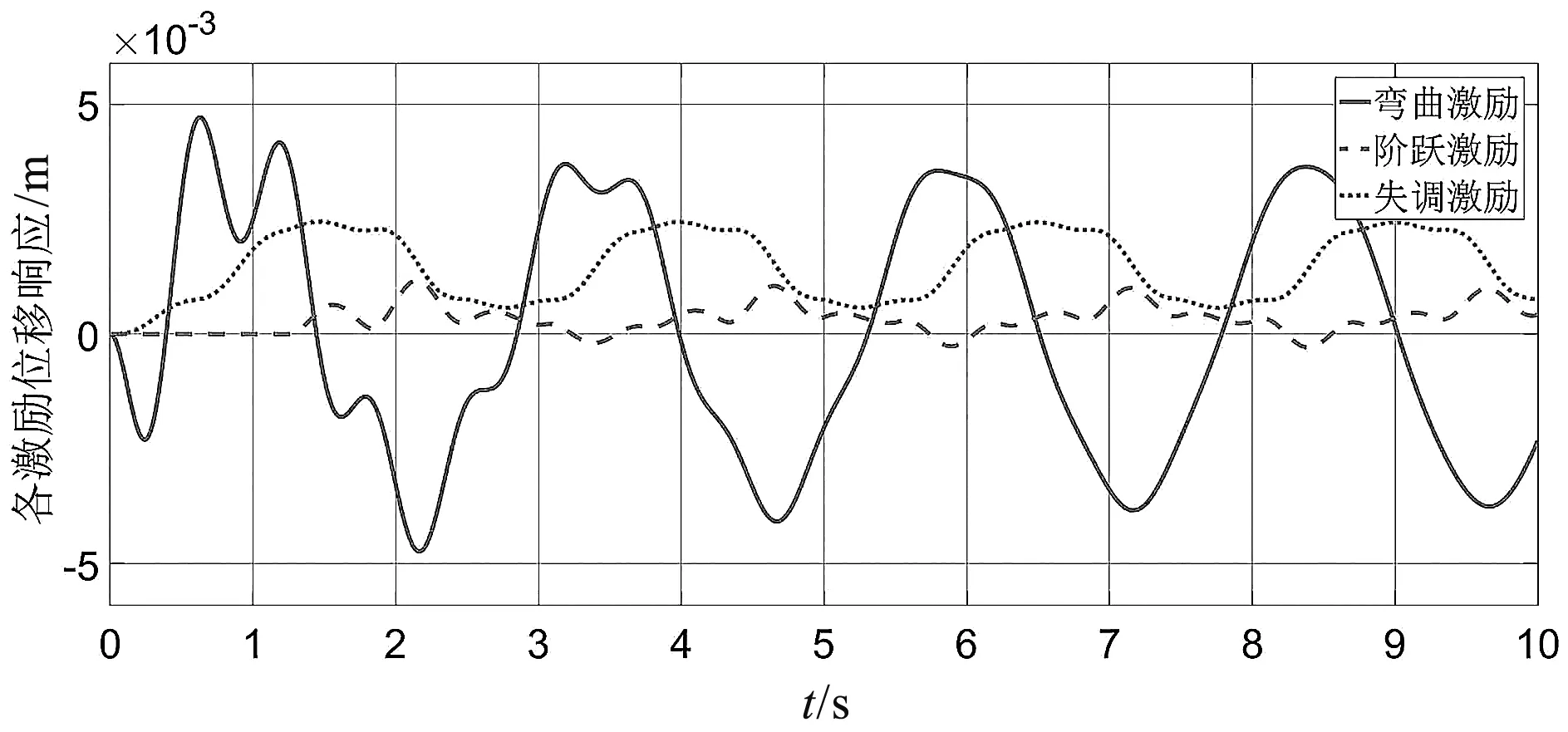
圖6 各激勵單獨作用下轎廂水平振動位移響應

由圖6可知:彎曲激勵對轎廂水平振動位移影響最大,失調(diào)激勵次之,而階躍激勵對轎廂水平振動位移影響較小。

各激勵單獨作用下轎廂水平振動速度響應如圖7所示。

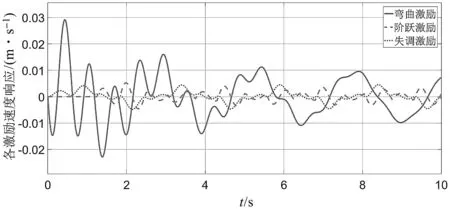
圖7 各激勵單獨作用下轎廂水平振動速度響應

由圖7可知:彎曲激勵對轎廂水平振動速度峰值影響較大,而另外兩種激勵對轎廂水平振動速度變化頻率影響更大。

各激勵單獨作用下轎廂水平振動加速度響應如圖8所示。

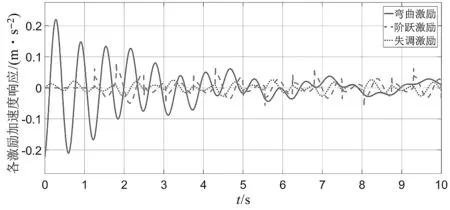
圖8 各激勵單獨作用下轎廂水平振動加速度響應

由圖8可知:彎曲激勵在運行前3 s內(nèi)對轎廂水平振動加速度幅度影響較大,之后趨于穩(wěn)定。由于激勵輸入圖像變化頻率較大,階躍與失調(diào)激勵對轎廂水平振動加速度變化頻率的影響較大。

4.1.2 多源激勵關聯(lián)轎廂水平振動特性分析

多源激勵耦合輸入如圖9所示。

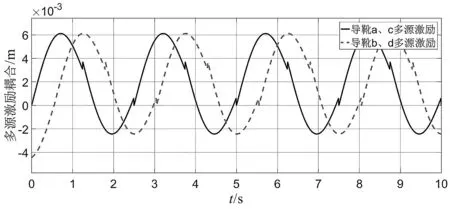
圖9 多源激勵耦合輸入

筆者綜合考慮多源激勵關聯(lián)性之間的影響,由前述Dematel方法計算出各激勵的重要度,得到多源激勵耦合輸入,之后進行多源激勵耦合振動仿真。

多源激勵關聯(lián)轎廂水平振動響應如圖10所示。

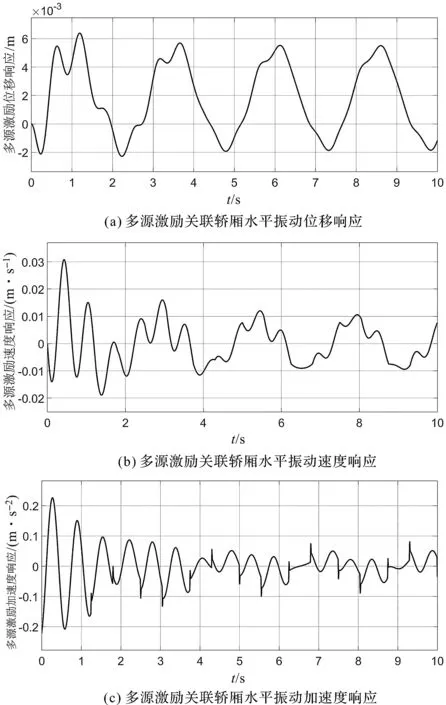
圖10 多源激勵關聯(lián)轎廂水平振動響應

由圖10可知:轎廂的水平振動位移變化較為規(guī)律,變化過程中存在一些波動,波動范圍為-2×10-3m～7×10-3m;轎廂水平振動速度在前2 s內(nèi)峰值較大,大約在-0.02 m/s～0.03 m/s之間波動,之后趨于平緩。轎廂水平動加速度同樣在前2 s內(nèi)峰值較大,大約在-0.22 m/s2～0.23 m/s2之間波動,之后逐漸趨于穩(wěn)定。

同理,多源激勵關聯(lián)轎廂水平轉(zhuǎn)動響應如圖11所示。

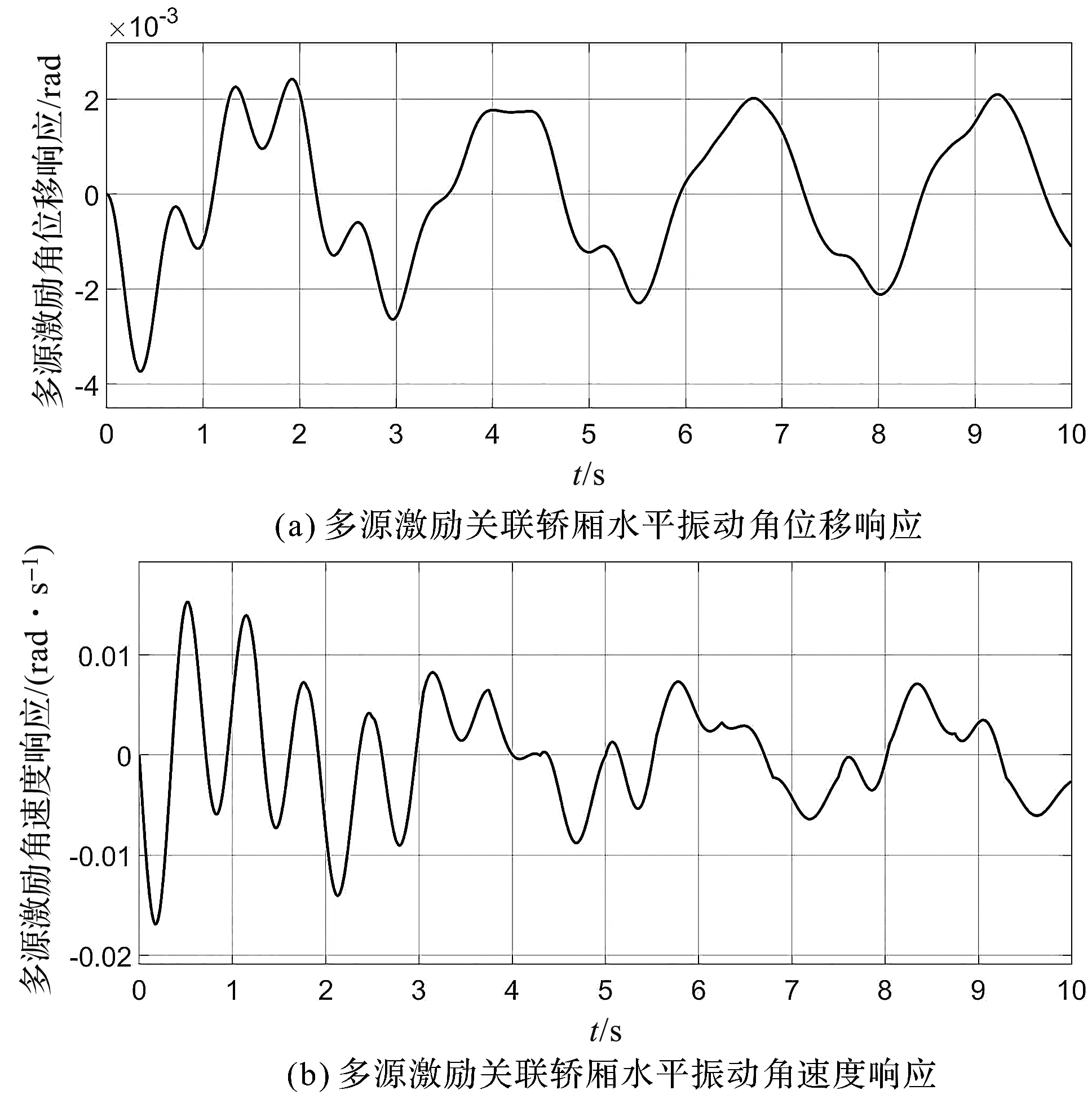
圖11 多源激勵關聯(lián)轎廂水平轉(zhuǎn)動響應

由圖11可知:轎廂的水平振動角位移變化趨勢與位移變化相似,同樣在變化過程中存在一些波動,波動范圍為-3.8×10-3rad～2.5×10-3rad;轎廂水平振動角速度在前2 s內(nèi)變化較為劇烈,大約在-0.017 rad/s～0.016 rad/s之間波動,之后趨于穩(wěn)定;轎廂水平振動角加速度在前3 s內(nèi)變化劇烈,在-0.14 rad/s2～0.15 rad/s2之間波動,之后逐漸趨于穩(wěn)定。

4.2 振動響應樣本數(shù)據(jù)準備

拉丁超立方抽樣方法能夠有效地填充樣本空間,抽取較少樣本就可以獲得較高計算精度。筆者將影響高速電梯水平振動的關鍵參數(shù)(導靴等效剛度、導靴等效阻尼、上方導靴到轎廂質(zhì)心的垂直距離、下方導靴到轎廂質(zhì)心的垂直距離)作為預測模型輸入?yún)?shù),其余參數(shù)固定不變,使用MATLAB編程,進行拉丁超立方抽樣,得到220組隨機樣本。

筆者將水平振動加速度峰值和水平振動角加速度峰值作為輸出參數(shù),將Simulink仿真得到的數(shù)據(jù)作為預測模型訓練數(shù)據(jù)和測試數(shù)據(jù);隨機選取20組樣本作為測試數(shù)據(jù),剩余的200組樣本作為訓練數(shù)據(jù)。

部分振動響應樣本數(shù)據(jù)如表3所示。

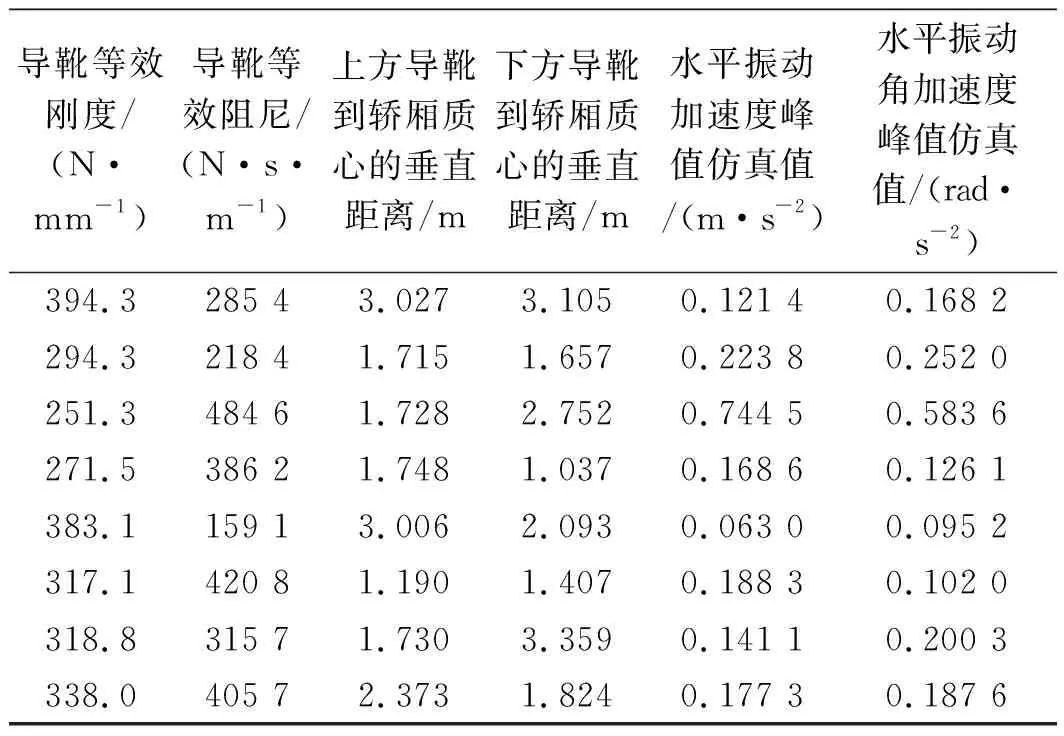
表3 部分振動響應樣本數(shù)據(jù)

由于各個變量并不處于同一個數(shù)量級,需要采用歸一化操作后進行模型訓練,同時為了便于對比,預測值需要反歸一化處理后,再進行對比分析。

4.3 預測模型訓練

筆者使用200組訓練集數(shù)據(jù)訓練CS-SVR模型,并重復若干次實驗,選取最優(yōu)的參數(shù)C值為1.74,γ值為0.27。

SVR優(yōu)化參數(shù)如表4所示。

表4 SVR優(yōu)化參數(shù)

4.4 討論

4.4.1 導軌多源激勵關聯(lián)性結(jié)果分析

考慮各激勵之間關聯(lián)性,筆者采用Dematel方法計算出各激勵的中心度和原因度,再由中心度和原因度計算出各激勵重要度,最終計算結(jié)果為:失調(diào)激勵重要度h1=0.300 7,彎曲激勵重要度h2=0.564 1,階躍激勵重要度h3=0.135 2。

4.4.2 仿真值與預測值的對比

網(wǎng)絡訓練完成之后,筆者使用測試集數(shù)據(jù)測試各個模型的預測效果。

仿真值與預測值對比如圖12所示。

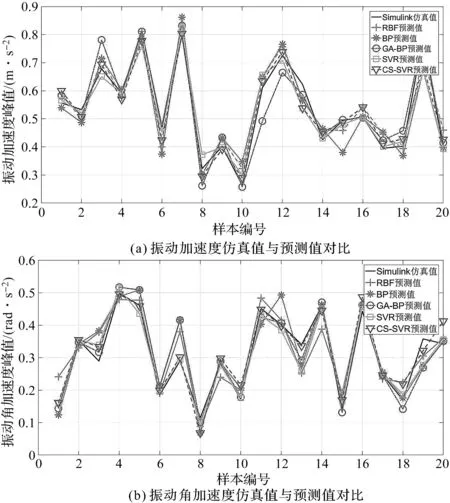
圖12 仿真值與預測值對比

4.4.3 預測方法性能對比分析

筆者采用決定系數(shù)、均方誤差、平均相對誤差和最大相對誤差評價各預測方法性能。

預測方法性能對比分析如表5所示。

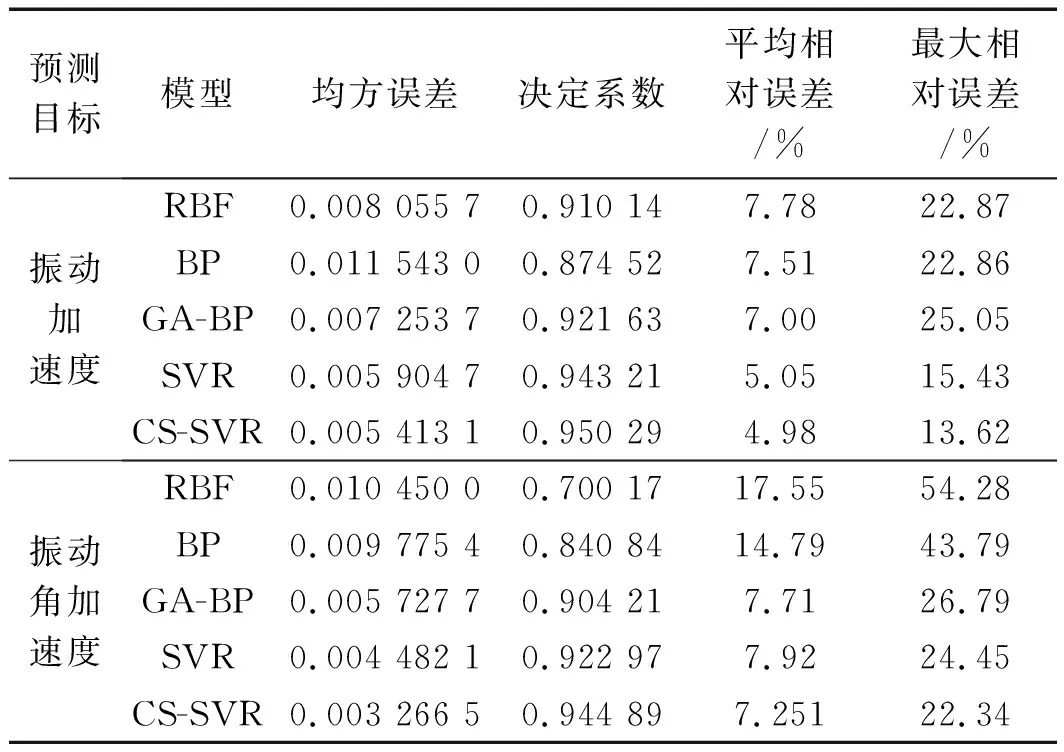
表5 預測方法性能對比分析

從均方誤差的角度可以得出:CS-SVR預測模型均方誤差最小,其次是傳統(tǒng)SVR模型和遺傳算法優(yōu)化的BP神經(jīng)網(wǎng)絡模型GA-BP,而均方誤差最大的模型是傳統(tǒng)的BP神經(jīng)網(wǎng)絡模型;從決定系數(shù)的角度可以得出:CS-SVR預測模型的決定系數(shù)最大,說明CS-SVR預測模型對樣本數(shù)據(jù)擬合效果較好,且沒有發(fā)生過擬合現(xiàn)象。CS-SVR預測模型平均相對誤差最小,且最大相對誤差也最小。

結(jié)合各項指標得出:CS-SVR預測模型預測效果最優(yōu),更適用于對高速電梯水平振動進行預測。

4.4.4 KLK2型康力高速電梯樣機振動性能實驗

為了驗證本文所提仿真與預測方法的準確性,筆者使用康力企業(yè)電梯實驗塔,對KLK2型號高速電梯樣機進行了實驗,使用PMT EVA-625分析儀得到了該高速電梯實際水平振動響應。

KLK2樣機實驗與本文方法結(jié)果對比如表6所示。

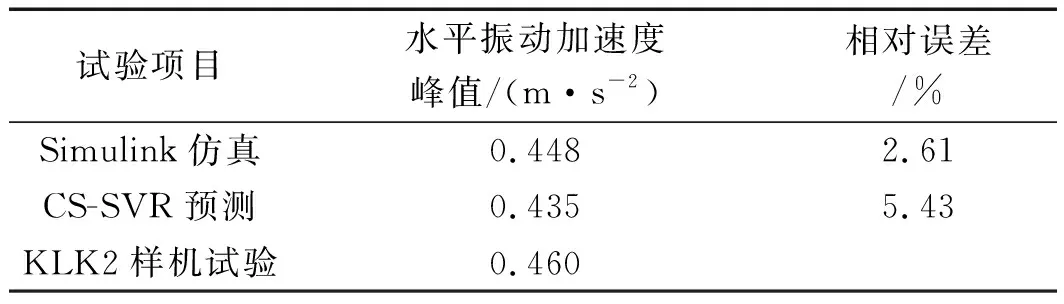
表6 KLK2樣機實驗與本文方法結(jié)果對比

表6顯示:Simulink仿真與KLK2樣機實驗相比誤差約為2.61%,本文所提CS-SVR預測結(jié)果與Simulink仿真相比誤差約為2.90%,CS-SVR預測結(jié)果與KLK2樣機實驗相比誤差約為5.43%。

由于實驗過程中存在安裝誤差和測量誤差,仿真誤差與預測誤差在可接受的范圍之內(nèi)。

5 結(jié)束語

由于高速電梯導軌多源激勵存在關聯(lián)性和在多源激勵耦合作用下引起轎廂水平振動的問題,筆者提出了基于導軌多激勵關聯(lián)的轎廂水平振動預測方法,進行了以下研究工作,并得出以下結(jié)論:

(1)分析了高速電梯導軌對轎廂水平振動的多源激勵影響因素,通過Dematel方法對導軌多源激勵進行了關聯(lián)性分析,得到了導軌多源激勵關聯(lián)重要度;結(jié)果表明,彎曲激勵重要度較大,階躍激勵較小;

(2)使用仿真與機器學習相結(jié)合的方法,建立了CS-SVR、SVR、RBF、BP、GA-BP預測模型,并進行了對比實驗;采用決定系數(shù)、均方誤差、平均相對誤差和最大相對誤差,對預測模型進行了評價;結(jié)果表明,CS-SVR模型預測效果最優(yōu);

(3)通過康力電梯樣機進行了對比實驗,驗證了本文所提方法的有效性。

本文僅對高速電梯振動預測方面進行研究,下一步擬開展高速電梯振動控制方面的研究。