鉸接輪式裝載機的橫向動力學建模分析*

王順桀,劉前結,李晨陽,葉軍君,祝青園

(廈門大學 機電工程系,福建 廈門 361102)

0 引 言

鉸接輪式裝載機是世界上使用量最大的工程機械之一[1],其主要功能是對松散物料進行鏟裝及短距離運輸作業。鉸接輪式裝載機的車身結構主要包含前、后兩個鉸接相連的車體,通過液壓缸推動活塞控制前、后車體之間的偏航角,以實現轉向[2]。由于鉸接輪式工程車輛具有變結構、變質心與變載荷等強非線性特點,同時包含鉸接液壓轉向、前后車體與后軸擺動橋,其動力學模型的建立存在困難。

由于鉸接輪式裝載機結構的特殊性,國內外學者對其動力學模型進行了深入的研究。

黃建等人[3]利用ADAMS對不同工況下鉸接輪式裝載機鏟斗液壓系統進行了仿真,為鉸接輪式裝載機的設計提供了參考依據。汪建春等人[4]為了簡鉸接輪式工程車輛的原地轉向動力學模型,將車輛的原地運動簡化為以較重車車軸中點為曲柄固定點的曲柄連桿運動,但該動力學模型不適用于行駛過程中的鉸接輪式工程車輛。竇鳳謙等人[5]建立了地下礦用鉸接裝載機的動力學模型,并將其運用于實際,實現了對裝載機的路徑跟蹤和避障控制;但由于該研究假設車輛行駛路面為水平路面,該結果不適用于在非水平地面行駛的鉸接輪式裝載機。

同時,鉸接輪式裝載機變結構變質心的特點導致其易側傾失穩,因此,部分學者通過車輛行駛穩定性分析,將各種優化的約束指標應用于車輛動力學模型的建模與分析。

AZAD N L等人[6]建立了鉸接輪式裝載機的水平運動線性模型,初步分析了裝載機的行駛穩定性;但由于其線性簡化,不適用于大轉向角轉彎的情況。賓澤云等人[7]通過建立水平地面上的鉸接輪式裝載機動力學模型,分析了速度對車輛行駛穩定性的影響,但沒能給出定量的約束指標。祝青園等人[8]圍繞鉸接輪式裝載機的橫向穩定性和動力學模型進行研究,提出了穩態余量角等橫向穩定性指標;但由于沒考慮轉向角改變引起的慣性力,因此,該結果難以適用于轉向角改變的車輛動態行駛過程。

在其他方面的研究中,通常還會利用橫向加速度和橫擺角速度對橫向穩定性進行評價[9,10],但因為鉸接輪式裝載機具有變結構與變質心特性,所以,此類常規車輛約束性指標難以準確反映鉸接輪式裝載機的側傾穩定性。

上述研究所提出的動力學模型均假設車輛行駛路面為水平路面,沒有考慮地面傾斜引起的重力、輪胎垂直載荷力等動力學參數改變,不適用于非水平地面;部分動力學模型難以準確描述行駛過程中,鉸接轉向角改變引起的動力學特性變化。并且,現有的鉸接輪式裝載機橫向動力學模型對模型約束性考慮較少,此類約束性指標難以準確反映其非結構環境中變轉向角行駛的側傾穩定性。

為此,筆者建立鉸接輪式裝載機橫向動力學模型,并進一步分析動力學模型的約束條件,通過比例樣機行駛實驗,來驗證動力學模型的有效性。

1 鉸接輪式裝載機動力學建模

為了建立鉸接輪式裝載機的橫向動力學模型,筆者首先分析液壓轉向系統的結構和動力學原理,然后通過裝載機坐標系和全局坐標系的轉換,建立其前、后車體的運動學模型,并進一步構建整車的橫向動力學模型,分析在動力學特點下裝載機動力學模型的約束條件。

為驗證模型的有效性,筆者搭建比例樣機進行側翻約束實驗和轉向行駛實驗,其技術路線如圖1所示。

圖1 鉸接輪式裝載機動力學建模流程圖

1.1 液壓轉向系統分析

液壓轉向系統是影響裝載機轉向行駛規律的主要部件,因此,建立裝載機的橫向動力學模型需要對其進行分析。

鉸接輪式裝載機液壓轉向活塞的布置如圖2所示。

圖2 活塞長度與轉向角關系的示意圖

在圖2中,A、B點與后車體鉸接,C、D點與前車體鉸接。以鉸接中心為圓心、后車體為參照,前車體繞后車體相對轉動。設∠AOA1=∠BOB1=α,∠AOC=∠BOD=α0,AC=A1C=a,BD=B1D=b,可以獲得轉向角與活塞AC軸長度p1的關系為:

(1)

車輛液壓轉向系統的結構剛度通常為常數KR,設轉向系統交界處的摩擦阻力和泄漏引起的阻尼為扭轉阻尼CR,則液壓缸產生的轉向力矩[11]為:

(2)

通過上述公式可以獲得活塞長度與轉向角的關系,同時獲得轉向力矩,以用于前后車體的動力學建模。

1.2 前后車體運動學分析

為了獲取裝載機的運動軌跡,需要對其進行運動學分析,建立車輛坐標與全局坐標之間的聯系,獲得前后車體之間動力學參數的耦合關系。

在常規車輛的運動學和動力學模型研究中,常使用單車模型[12]對運算過程進行簡化。單車模型將常規車輛4個前后車輪簡化為在車輛中心軸上的2個等效車輪。等效后輪與車體方向一致,等效前輪轉動可以改變行駛方向。等效簡化法可顯著地縮減模型的計算量,提高運算效率。相比于常規車輛,鉸接輪式工程車輛沒有轉向輪,而是通過改變前后車體之間的轉向角來實現轉向。

因此,筆者建立鉸接轉向單車模型,如圖3所示。

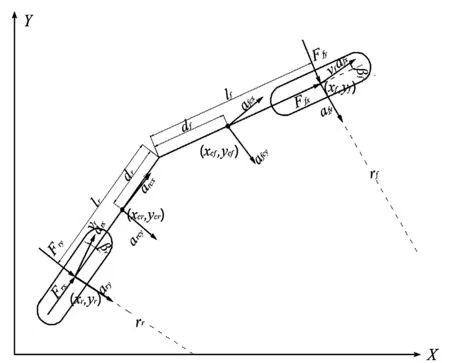
圖3 鉸接轉向單車模型xcf—前車體質心橫坐標;ycf—前車體質心縱坐標;xcr—后車體質心橫坐標;ycr為—后車體質心縱坐標;xf—前車軸中點橫坐標;yf—前車軸中點縱坐標;βf—等效前輪的側偏角;βr—等效后輪的側偏角;df—前車體質心到鉸接點距離;dr—后車體質心到鉸接點距離;lf—前軸中點到鉸接點的距離;lr—后軸中點到鉸接點的距離;rf—前車體行駛的曲率半徑;rr—后車體行駛的曲率半徑;vfx—前軸中點縱向速度;vfy—前軸中點橫向速度;vrx—后軸中點縱向速度;vry—后軸中點橫向速度;arcx—后車體質心縱向加速度;arcy—后車體質心橫向加速度;afcx—前車體質心縱向加速度;afcy—前車體質心橫向加速度;afy—前軸中點橫向加速度;afx—前軸中點縱向加速度;ary—后軸中點橫向加速度;arx—后軸中點縱向加速度;Ffy—等效前輪橫向力;Ffx—等效前輪縱向力;Fry—等效后輪橫向力;Frx—等效后輪縱向力

在圖3中,以前軸和后軸的中點速度作為簡化模型前后車輪的速度,通過改變前后車體之間的夾角,以改變行駛方向。根據前后車體相對關系可以得到車體結構主要位置全局坐標:

(3)

(4)

(5)

(5)

式中:xo—車輛整體運動瞬心橫坐標;yo—車輛整體運動瞬心縱坐標;ρf—前車體行駛曲率;ρr—后車體行駛曲率;kf—前車體與x軸正方向的夾角;kr—后車體與x軸正方向的夾角。

(7)

(8)

式中:mr—后車體質量;mf—前車體的質量。

根據鉸接輪式工程車輛運動學規律可知:

(9)

(10)

式中:βcf—前車體質心等效側偏角;βcr—后車體質心等效側偏角;ωf—前車體轉動角速度;ωr—后車體轉動角速度。

將前車體的加速度分解為后車體的加速度與相對后車體的加速度的矢量和,即:

(11)

鉸接輪式工程車輛變轉向角轉向行駛時,在車輛坐標系中需要考慮前后車體相對運動產生的科氏加速度。根據科氏加速度定義,前后車體科氏加速度為:

(12)

式中:vrr—后車體質心相對于轉動系的相對速度;vrf—前車體質心相對于轉動系的相對速度。

在任意轉向角下,鉸接輪式工程車輛的側傾中心都與OfOr平行。以OfOr為參考系,可得前后車體科氏加速度垂直于OfOr的分量acrn、acfn:

(13)

式中:cf—前車體質心到前軸的距離在xf方向的投影長度;cr—后車體質心到后軸的距離在xr方向的投影長度。

通過以上運動學分析,筆者獲得了前后車體的運動學關系,解算了鉸接輪式工程車輛動力學建模所需的運動學參數。

1.3 車輛動力學模型

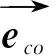
在傾角為φ的斜坡上,車輛前后車體的受力情況如圖4所示。

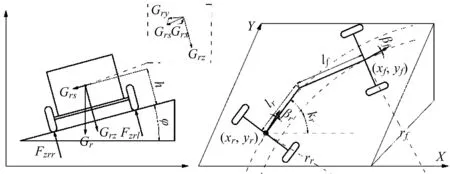
圖4 斜面上的鉸接輪式工程車輛示意圖Grx—后車體重力的縱向分量;Gry—后車體重力的橫向分量;Gr—后車體重力;Grz—后車體重力垂直于斜面的分量;Grs—后車體重平行于斜面的分量;Fzrr—右后輪垂直載荷力;Fzrl—左后輪垂直載荷力

將前后車體重力如圖4進行分解,可得:

(14)

式中:Gfx—前車體重力的縱向分量;Gfy—前車體重力的橫向分量。

由車輪垂直載荷力與車輛重力垂直于斜面的分力平衡,可得:

Fzr+Fzl=(Gr+Gf)cosφ

(15)

式中:Gf—前車體重力;Fzl—左側車輪垂直載荷力;Fzr—右車輪垂直載荷力。

根據動力學分析,可以得到重力和車輪垂直載荷力對OrOf上的力矩Lg、Lz:

(16)

(17)

式中:hf—前車體的質心高度;hr—后車體的質心高度;θp—OrOf的俯仰角。

在車輪側偏角滿足αt≤7°時,魔術公式能夠準確反映輪胎的動力特性[13-15]。設輪胎的側偏剛度為Ct,可得側偏角與輪胎側向力的簡化公式如下:

(18)

式(18)還可轉化為:

(19)

分別計算兩個車體的慣性力,可得:

(20)

(21)

式中:Fifx—地面坐標系下前車體縱向慣性力;Fify—地面坐標系下前車體橫向慣性力;Firx—地面坐標系下后車體縱向慣性力;Firy—地面坐標系下后車體橫向慣性力;Finf—車輛坐標系下前車體在垂直于OfOr方向的慣性力;Finr—車輛坐標系下后車體在垂直于OfOr方向的慣性力。

在車輛OfOr參考系下,車體相對運動的科氏力和慣性力共同決定的側傾力矩為:

Li=(mracrn+Firn)hr+(mracrn+Fifn)hr

(22)

根據達朗貝爾原理,考慮液壓轉向系統轉向力矩,筆者建立車輛整體平動和前后車體轉動的動力學平衡方程如下:

(23)

式中:Jfz—前車體對Zf方向的轉動慣量;Jrz—后車體對Zr方向的轉動慣量。

將上述動力學模型的微分方程轉化為狀態方程的形式:

R(x,u)=F(x,u)

(24)

X、R(x,u)與F(x,u)可整理為:

X=[vrxβcrβcfωrα]T

(25)

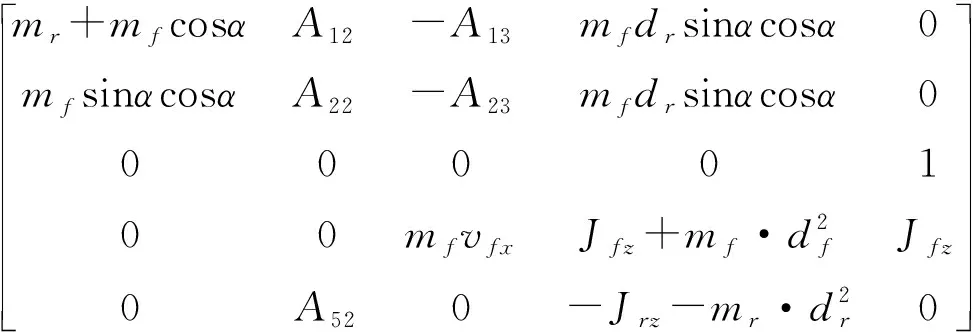
(26)

(27)

式中:

A12=mfvrxsinαcosα

(28)

A13=mf[vrxcosα+(ωdr-vrxβcr)sinα]sinα

(29)

A22=mfvrxsin2α+mrvrx

(30)

A23=mf[vrxcosα+(ωdr-vrxβcr)sinα]cosα

(31)

A52=-mrvrx·dr

(32)

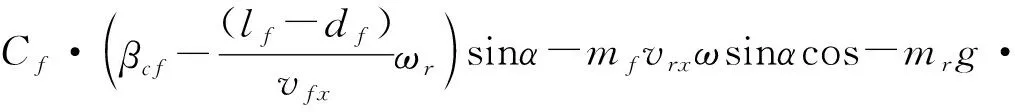
(33)

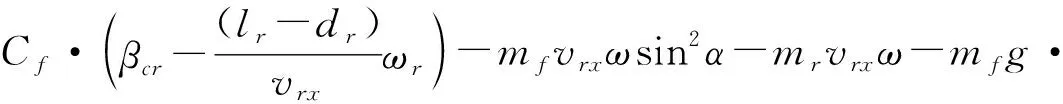
(34)

(35)

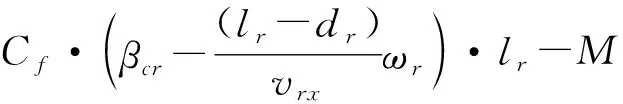
(36)

鉸接輪式工程車輛的動力學模型最終可表述為:

(37)

1.4 動力學模型約束

在完成鉸接輪式裝載機動力學建模之后,需要為動力學模型添加合適的約束條件,包括車輛結構決定的約束條件、輪胎模型的有效性約束條件與側傾失穩約束條件等。

鉸接輪式裝載機的穩定性是其動力學建模的主要研究內容之一,提高傾斜地面動態行駛過程中的抗側傾穩定性對于鉸接輪式裝載機行駛安全具有重要意義。其側傾失穩與各種因素有關,例如質心變化、車輛姿態變化、車輛整體運動和內部結構相對運動。

橫向載荷轉移率(LTR)通常被用于描述常規車輛的側翻穩定性指標[16],其公式為:

(38)

LTR值在0～1之間變化,其中,LTR為0,代表兩側車輪載荷相等,車輛穩定行駛;LTR值為1,代表車輛載荷集中在一側車輪,車輛即將側傾[17,18]。然而在實際行駛過程中,裝載機的輪胎垂直載荷力難以準確測量,同時,裝載機車體變結構會引起側傾中心與車輛相對位置變化,故LTR無法直接適用于鉸接輪式裝載機。

綜合考慮傾斜地面下的車地相對位姿、車輛整體和前后車體運動、轉動參考系下的科氏力等因素,筆者對鉸接輪式裝載機的側傾動力學進行了分析,在前后軸中點線OfOr參考系中有:

Jfγf+Jrγr=Lz+Lg+Li

(39)

式中:Jf—前車體對OfOr的轉動慣量;Jr—后車體對OfOr的轉動慣量;γf—前車體對OfOr的角加速度;γr—前后車體對OfOr的角加速度。

Lz、Lg、Li由式(15,16,21)確定。通過轉動慣量的合成原理和運動矢量疊加原理可知:

(40)

(41)

式中:Jfx—前車體縱向轉動慣量;Jrx—后車體縱向轉動慣量;γfx—前車體縱角加速度;γrx—后車體縱向角加速度;Jfy—前車體橫向轉動慣量;Jry—后車體橫向轉動慣量;Jfxy—前車體縱向和橫向慣性積;Jrxy—后車體縱向和橫向慣性積。

在車輛尚未側翻時,其對于OfOr的角加速度為0,聯立式(15～17,22,38～41),可獲得鉸接輪式裝載機的橫向載荷轉移率(avLTR),即:

(42)

根據鉸接輪式裝載機的結構特點,結合車輛動力學模型中常用的失穩約束,以及輪胎模型的有效性范圍,給出以下約束條件:

(43)

式中:γ—后車軸與后車體之間的夾角。

2 動力學模型實驗及結果分析

為了驗證動力學模型的有效性,基于搭建的鉸接輪式裝載機1 ∶4比例樣機,筆者進行實驗測試。比例樣機由鋁型材搭建框架,后軸中點與后車體鉸接,以輪轂電機為驅動,前后車體鉸接連接,通過電推桿實現轉向控制;比例樣機模型以實際鉸接裝載機的結構特征為參照,與實際車輛的相似性較高,能夠滿足其動力學實驗的需求。

比例樣機的構成如圖5所示。

圖5 比例樣機及主要傳感器

該樣機通過轉向推桿讀取其伸長量,通過旋轉編碼器獲得前后車體的轉向角,通過輪速傳感器獲得車速,并利用后車體質心位置安裝的IMU采集加速度、角速度和姿態等信息,利用IMU采集的姿態信息對加速度進行修正,去除三軸重力加速度分量獲得比例樣機的實際運動加速度,并根據IMU和GPS定位信息生成行駛軌跡。

比例樣機搭載的主要傳感器型號如表1所示。

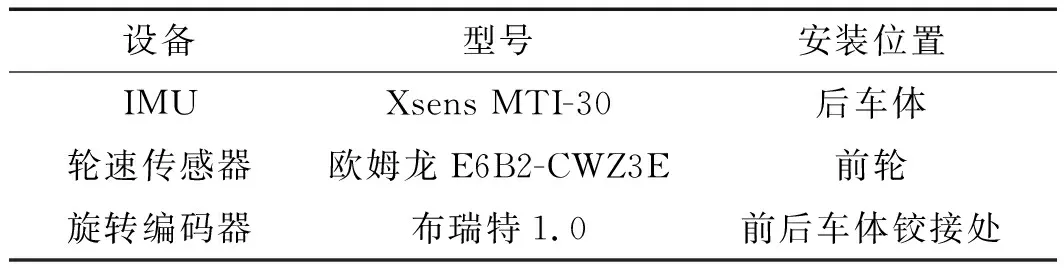
表1 比例樣機搭載的主要傳感器

車體主要參數如表2所示。

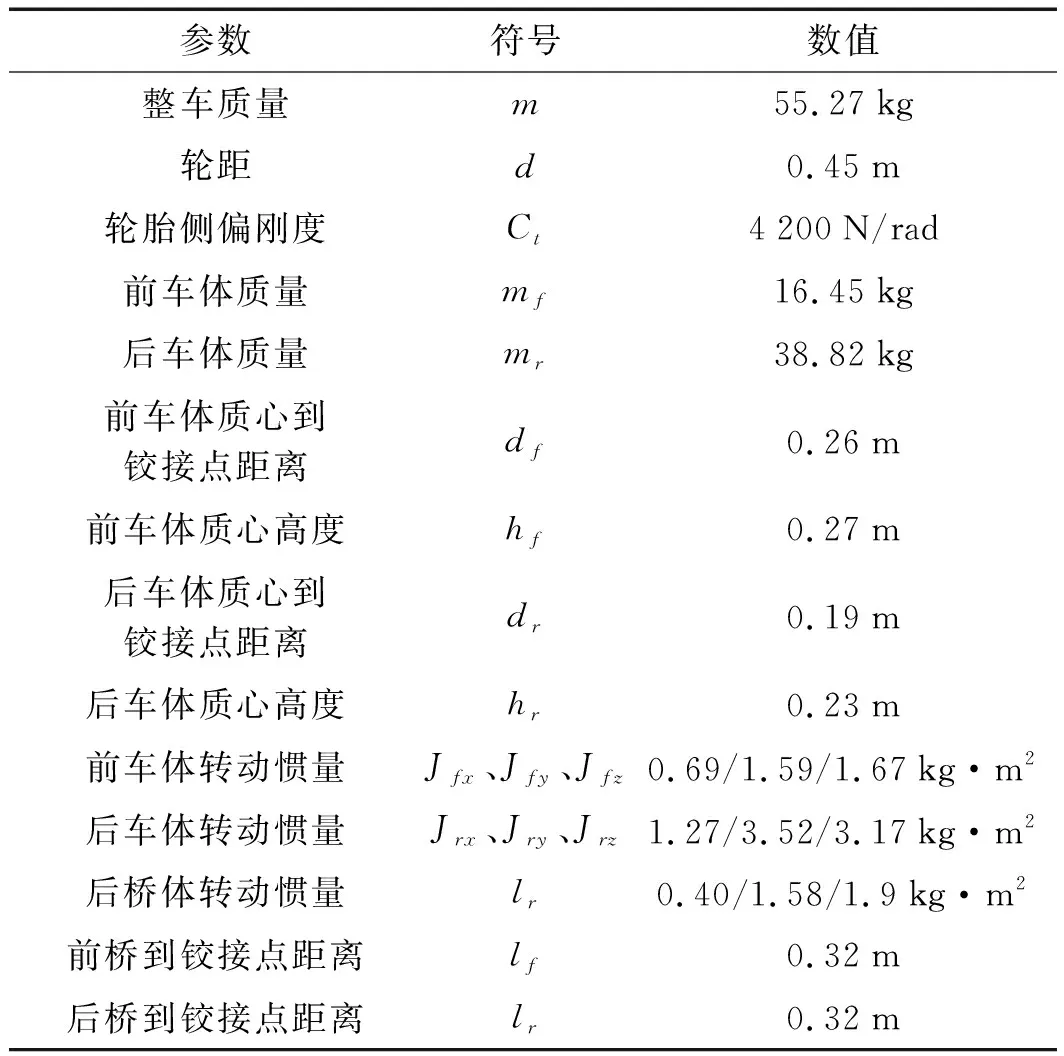
表2 比例樣機模型主要參數

2.1 側傾約束驗證實驗

針對鉸接輪式裝載機動力學模型的側傾約束指標,需要對其有效性進行驗證,而定轉角加速實驗和魚鉤工況實驗是車輛最常用的橫向穩定性實驗。

因此,筆者利用搭建的比例樣機進行非結構環境下定轉向角加速側傾實驗和魚鉤工況側傾實驗,以記錄下比例樣機側傾的時刻,并通過IMU、輪速傳感器和旋轉編碼器記錄動力學參數和轉向角參數,代入式(42),解算側傾前后的avLTR值,并進行對比分析。

在定轉向角加速側傾實驗中,筆者控制轉向角保持在30°,不斷增加車速至一側車輪離地,定轉向角加速實驗如圖6所示。

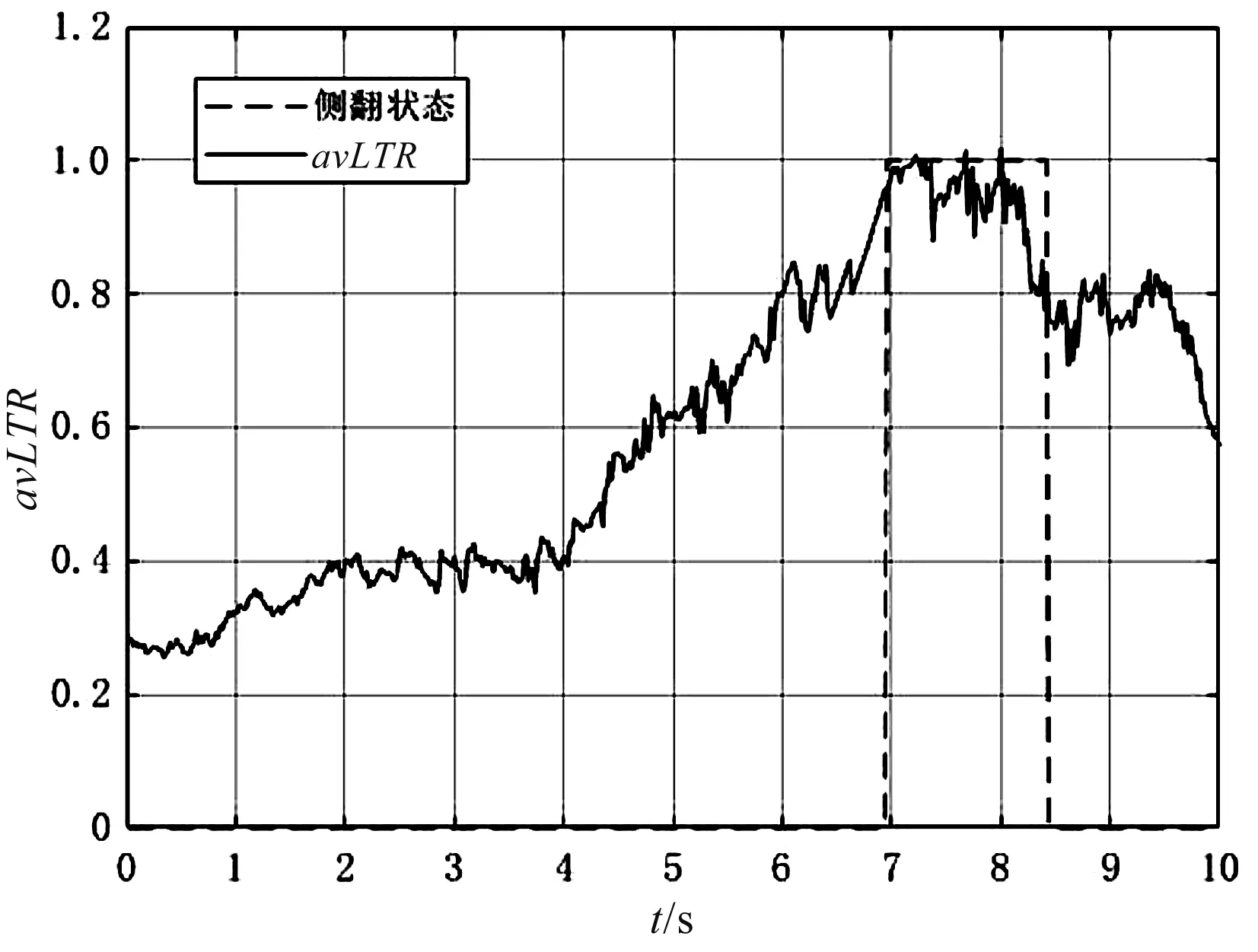
圖6 定轉向角加速側傾實驗

圖6中,在5.76 s時,avLTR到達閾值0.7,在隨后的6.92 s時刻,比例樣機已經開始側傾,單側車輪已駛離地面,此時avLTR值為0.97,該結果與實際車輛側翻狀態吻合。

在魚鉤工況側傾實驗中,筆者控制比例樣機進行加速行駛,然后控制電動推桿伸長,增大轉向角至單側車輪離地,魚鉤工況側傾實驗如圖7所示。

由圖7可得,avLTR在7.92 s時刻到達閾值0.7,

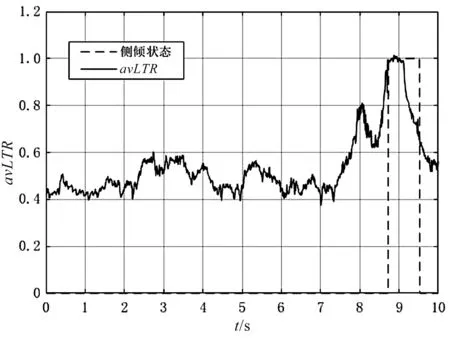
圖7 魚鉤工況側傾實驗

但車輛并沒有隨即側翻;隨后筆者控制車輛繼續加速行駛,比例樣機在8.74 s時刻開始側傾,此時avLTR值到達1,車輛已完全側翻。

以上的定轉向角加速側傾和魚鉤工況側傾實驗結果表明:筆者提出的適用于鉸接輪式裝載機的avLTR可以較好地反映比例樣機行駛過程中的橫向穩定性。因此,通過合理地設置avLTR閾值,可以作為側傾約束,防止樣機進入側傾危險工況。

實驗中,比例樣機的avLTR曲線存在比較明顯的波動,這也反映了模型車在野外運動的實際情況。相比于比例樣機,真實的鉸接輪式裝載機具有更大的質量和轉動慣量,在相同的路面行駛獲得的avLTR會更加穩定。

2.2 動力學模型驗證實驗

在動態行駛過程中,為了驗證動力學模型的準確性,筆者進行了曲線行駛實驗;設定后車體驅動輪速度設置為3 m/s,轉向推桿伸長率設為0.03 m/s。

曲線行駛下實驗結果與模型結果對比如圖8所示。

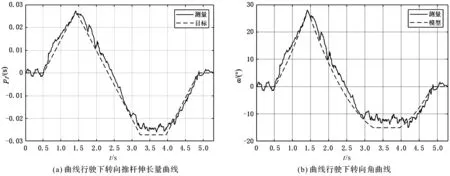
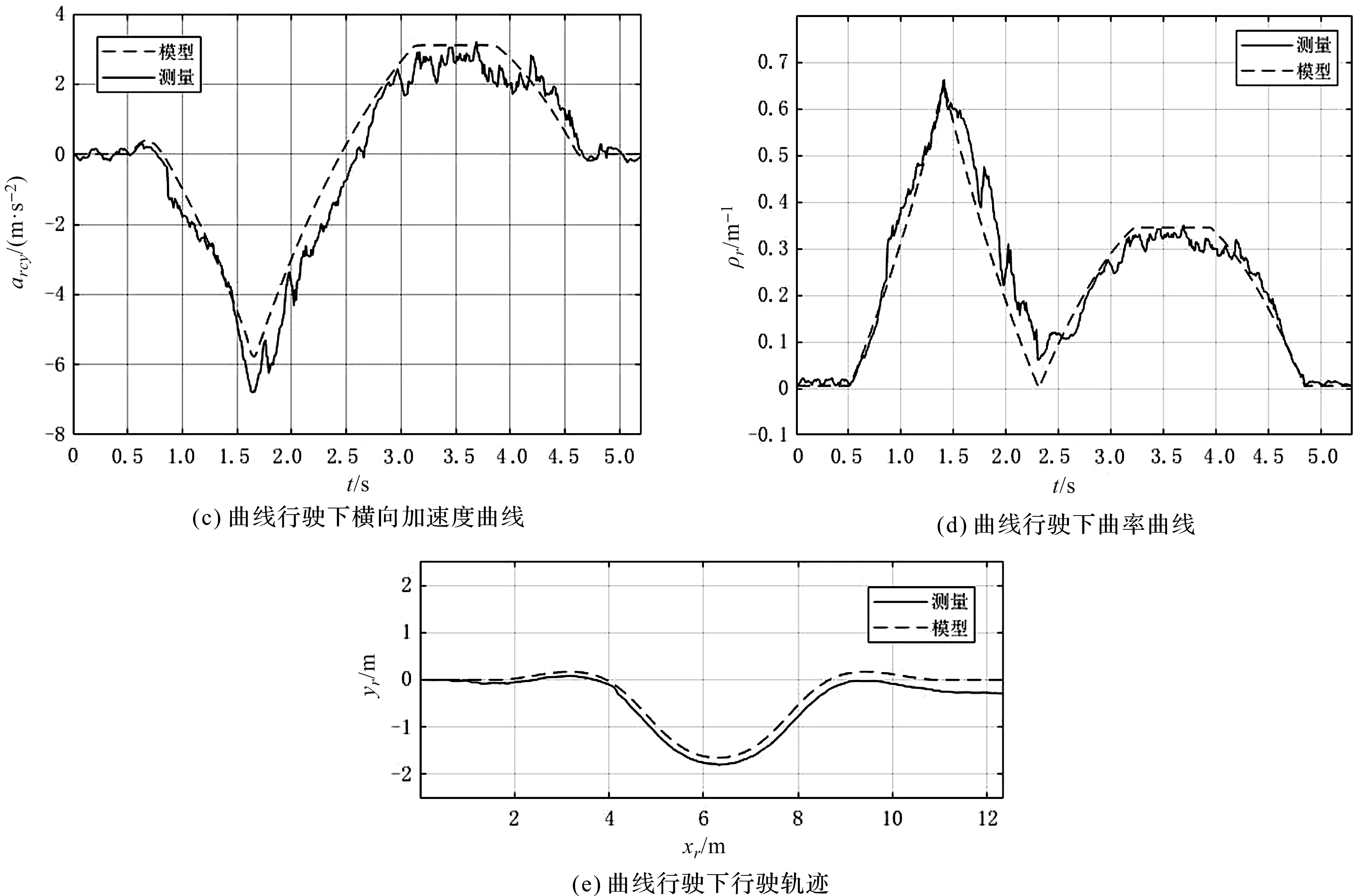
圖8 曲線行駛下實驗結果與模型結果對比

由圖8(a～d)可知:在曲線行駛實驗中,轉向推桿伸長量先增大后減小,隨后恢復到原長;轉向角變化趨勢與轉向推桿伸長量變化基本一致;模型的橫向加速度、曲率與實驗結果保持較好跟蹤趨勢。該結果表明,該動力學模型能夠有效地描述車輛的鉸接轉向與橫向動力學參數特性。

由圖8(b,e)可知:在推桿開始持續伸長后的0.9 s,比例樣機并沒有直接開始右轉,而是先向左行駛,再向右行駛,這種轉向遲滯現象是鉸接輪式裝載機獨特轉向機理引起的;在行駛初期階段,電動推桿伸長推動前后車體相對旋轉,給予前后車體相反方向的力偶矩,在該力偶矩作用下,車輛行駛速度小于液壓轉向速度,造成了前后車體轉向遲滯現象,使得轉向過渡處的模型誤差較大。

筆者建立的動力學模型較好地仿真模擬了鉸接輪式裝載機轉向遲滯現象,也證明了該動力學模型的有效性。

在實驗中,轉向角、橫向加速度、曲率、車輛位置以50 Hz頻率采樣,通過統計采樣時刻的測量值與模型值的誤差,通過計算可得到上述各項的誤差分布,如圖9所示。

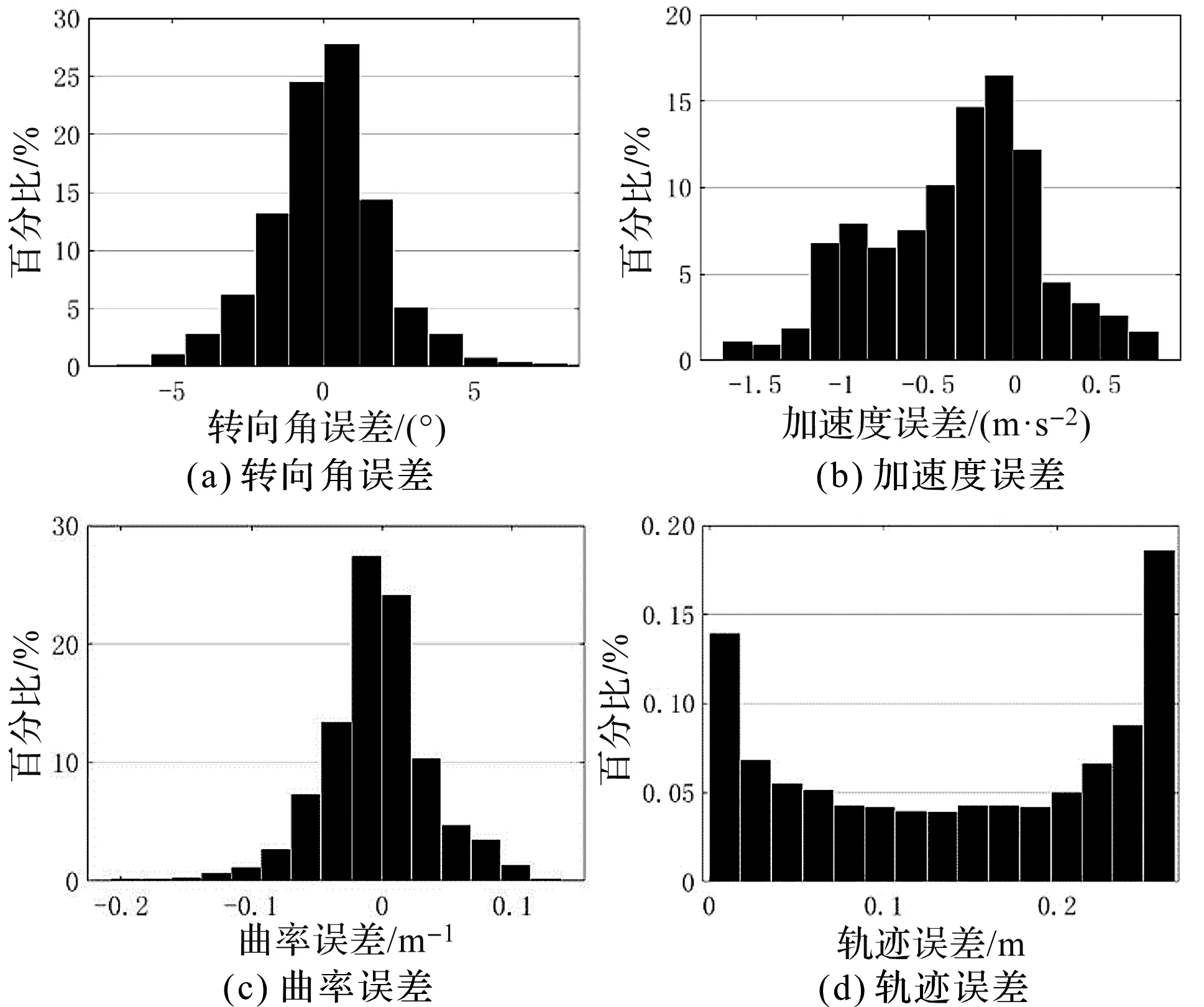
圖9 曲線行駛實驗誤差分布直方圖

圖9中,通過采樣點的誤差值可以獲得模型轉向角、橫向加速度、曲率與軌跡的均方根誤差,其均方根誤差分別為1.71°、0.89 m/s2、0.05 m-1、0.13 m;轉向角、橫向加速度、曲率的誤差分布在零值附近,而行駛軌跡由于存在累計誤差,在行駛初段軌跡誤差較小,行駛一段時間后軌跡誤差將逐漸變大,在誤差分布直方圖表現為誤差在較大值中分布較多。

總體上,實驗中的各項模型解算值與實際測試結果基本吻合。實驗結果進一步表明,該動力學模型能夠較好地描述鉸接輪式裝載機的橫向動力學特性。

3 結束語

針對非結構環境工況下,鉸接輪式裝載機的橫向動力學變化特性,筆者開展了相關動力學建模研究,利用達朗貝爾原理建立了鉸接輪式裝載機的動力學模型,分析了模型相關的約束條件,并通過搭建比例樣機,對其進行了驗證。

研究結果表明:

(1)所提出的側翻約束指標avLTR能準確地反映非結構環境中,鉸接輪式裝載機的橫向穩定性;對其設定合理的閾值,可將其作為動力學模型的側翻約束條件;

(2)在非結構環境行駛過程中,所建立的動力學模型能夠對車輛動力學變化特性進行準確的描述,同時可以較好地仿真模擬車輛的鉸接轉向遲滯現象。

該動力學模型的良好表現僅僅是在比例樣機上得到了實驗驗證,而沒有在實際大型非結構工況下的鉸接輪式裝載機上得到驗證。因此,接下來的研究中,筆者將在鉸接輪式裝載機上進一步開展實車驗證,以及進行動力學模型的應用研究。