八種方法求解一道希望杯經(jīng)典題
余鐵青
(廣東省中山市桂山中學(xué) 528463)
一、問題提出
一題多解沒有唯一和固定的模式,教師可以通過縱橫對(duì)比發(fā)散、知識(shí)串聯(lián)、綜合溝通等手段,由一題引發(fā)多種解答方法,為學(xué)生構(gòu)建完善的知識(shí)體系.教師可以引導(dǎo)學(xué)生從不同角度入手,用不同的解答方法完成解題,并以此來幫助同學(xué)們更加深刻地理解數(shù)學(xué)的本質(zhì)概念,掌握試題解答的思路與方法,幫助學(xué)生體會(huì)數(shù)學(xué)的多樣美感,激發(fā)數(shù)學(xué)學(xué)習(xí)興趣,拓寬學(xué)生思維的廣闊度.
二、實(shí)例分析
題目(第九屆希望杯全國數(shù)學(xué)邀請(qǐng)賽高一試題)若二次函數(shù)f(x)=ax2+bx,恒有f(x1)=f(x2)(x1≠x2),求f(x1+x2)的值.
策略1利用已知條件,直接帶入化簡,常規(guī)操作.
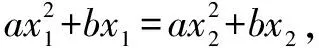
另一方面:f(x1+x2)=a(x1+x2)2+b(x1+x2)=(x1+x2)[a(x1+x2)+b],所以f(x1+x2)=0.
評(píng)注解數(shù)學(xué)題是有一定模式的,各種不同類型的題目有相應(yīng)的基本解題策略,這就是常說的“套路”,實(shí)際上就是我們講的“通性通法”.當(dāng)學(xué)生在測試中面對(duì)一道試題的時(shí)候,如果不能很快思考出最優(yōu)的策略,那么切不可忽略本源,即常見常用的解題思路,在時(shí)間不充足的情況下快速找到解決問題的策略是關(guān)鍵.畢竟時(shí)間有限,先得分,考完之后再進(jìn)行反思優(yōu)化是提高的必由之路,只會(huì)機(jī)械記住套路,甚至背套路是萬萬不提倡的,因?yàn)檫@會(huì)完全喪失解題的靈性.
策略2 進(jìn)行代數(shù)運(yùn)算時(shí),適當(dāng)進(jìn)行變形配方.
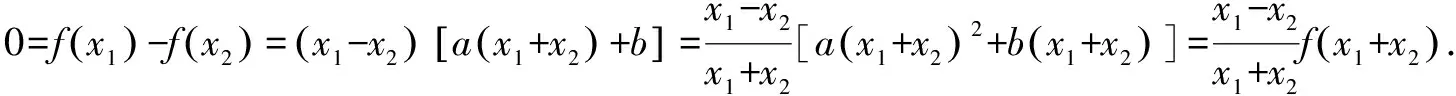
又因?yàn)閤1≠x2,所以f(x1+x2)=0.
評(píng)注該解法使用配方法改變了代數(shù)式的原有結(jié)構(gòu),從一個(gè)要求的結(jié)論出發(fā),整理配湊出我們希望出現(xiàn)的結(jié)構(gòu),再利用整體代換的思想直接得出結(jié)果,而這種思維是在日常學(xué)習(xí)中要著重鞏固的,不僅在該題有著很好的應(yīng)用,在其它不等式等相關(guān)試題中的應(yīng)用也是十分廣泛的,所以工具越多,解題越從容.
策略3聯(lián)想函數(shù)對(duì)稱軸,利用二次函數(shù)性質(zhì).
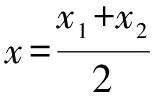
評(píng)注函數(shù)諸多性質(zhì)中,筆者最為推崇對(duì)稱性,這是數(shù)學(xué)美學(xué)的最淺顯的外在表征,當(dāng)然在此處不過多去討論奇偶性、單調(diào)性、周期性等.此解法有諸多巧合重疊,從函數(shù)對(duì)稱軸出發(fā),結(jié)合離函數(shù)對(duì)稱軸距離相等的自變量所對(duì)應(yīng)函數(shù)值相等這一結(jié)論使得對(duì)稱之美展現(xiàn)得淋漓盡致!其中,在2017年新課標(biāo)Ⅲ卷理11中的應(yīng)用亦是美妙至極.
策略4 構(gòu)造方程的根結(jié)合韋達(dá)定理.
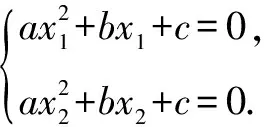
評(píng)注實(shí)際上,如果不設(shè)f(x1)=f(x2)=-c,直接將x1,x2代入f(x)的解析式得到方程組,亦可求得所要結(jié)果.這樣寫僅僅是為了和學(xué)生平時(shí)所認(rèn)知的一元二次方程形式進(jìn)行統(tǒng)一,做這樣的假設(shè)形式其實(shí)就是最近發(fā)展區(qū)理論,這能夠很好地和學(xué)生所固有的認(rèn)知契合,大家很容易接受,能夠有效提高教學(xué)效率.
策略5 利用抽象函數(shù)的廣義對(duì)稱性質(zhì).
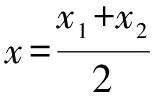
評(píng)注這種解法在于對(duì)抽象函數(shù)形式的理解和掌握,是前面解法的升華.因?yàn)樵擃惡瘮?shù)性質(zhì)實(shí)際上可以推廣到任意具備對(duì)稱性函數(shù)求值問題,這就比直接考慮二次函數(shù)對(duì)稱性的思維更加深刻.
策略6 構(gòu)造直線共線向量.
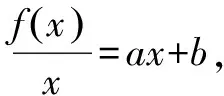
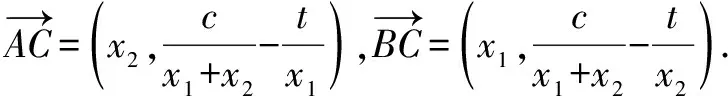
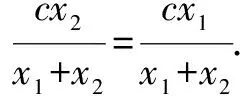
又x1≠x2,所以c=0.進(jìn)而f(x1+x2)=0.
評(píng)注該解法筆者是基于微分思想的角度聯(lián)想到的,“點(diǎn)線面”,“一維二維三維”是典型的思維遷移的模范!筆者試圖將二次函數(shù)降次理解構(gòu)造共線向量進(jìn)行理解,試過之后,發(fā)現(xiàn)著實(shí)可以這么理解,在講解中注重靈感思路的來源分析,能很好地啟迪學(xué)生.
策略7 由外形結(jié)構(gòu)f(x)=ax2+bx類比等差數(shù)列性質(zhì).
解法7 在等差數(shù)列{an}中,Sn是其前n項(xiàng)和,若Sm=Sn(m≠n),那么Sm+n=0.
結(jié)合f(x1)=f(x2)(x1≠x2),立馬可得f(x1+x2)=0.
評(píng)注類似思想可以在此處得到最大的恩寵,一時(shí)間復(fù)雜的問題在此刻得到了瞬間的釋放,這才是真正的秒解!是運(yùn)氣?是福氣?都不是,是能力的完美體現(xiàn)!
是日積月累的思考與探究!發(fā)現(xiàn)新的事物往往是由所熟悉的事物進(jìn)行遷移類比產(chǎn)生猜想,然后依賴于嚴(yán)謹(jǐn)?shù)耐评碚撟C進(jìn)行驗(yàn)證.猜想是做學(xué)問和鍛煉創(chuàng)新思維的出發(fā)點(diǎn),證明則是推理驗(yàn)證的落腳點(diǎn)與最終歸宿.
策略8 利用行列式三角形面積公式.

評(píng)注基于教學(xué)實(shí)際,筆者認(rèn)為學(xué)生有必要掌握該方法.首先,從高考命題角度與考試大綱要求來看,初等數(shù)學(xué)之中融入高等數(shù)學(xué)思想是命題的重點(diǎn)方向,類似的還有洛必達(dá)法則、端點(diǎn)效應(yīng)、泰勒展開等,這就是其中很好的一例!其次,從考試直接應(yīng)用來看,行列式求解三角形面積還廣泛存在于平面解析幾何之中,通過計(jì)算達(dá)到思路明晰,解題高效之效果.
縱觀以上八種不同解法,可以說一種更比一種妙!實(shí)際上一題多解更能很好地幫助學(xué)生構(gòu)建更加完善的知識(shí)體系,通過比較分析,會(huì)進(jìn)一步認(rèn)清哪些只是較為一般的解法,哪些是比較有創(chuàng)新的思路,哪種解法更簡單等,這樣能夠使得學(xué)生的思維更開闊、更清晰,從而靈活地把握知識(shí)間的橫向關(guān)系與縱向聯(lián)系,提高解決問題的能力,培養(yǎng)學(xué)生審慎的解題習(xí)慣,發(fā)揮學(xué)生的創(chuàng)造性.

