我國(guó)3種針葉林的材積源生物量模型研建
曾偉生
(國(guó)家林業(yè)和草原局調(diào)查規(guī)劃設(shè)計(jì)院,北京 100714)
森林生物量與森林蓄積量一樣,既是各級(jí)森林資源監(jiān)測(cè)的重要指標(biāo),更是反映森林生態(tài)系統(tǒng)生產(chǎn)力的重要參數(shù)[1-3]。對(duì)森林生物量的估計(jì),既可通過建立立木生物量模型來獲得[4-5],也可通過建立林分生物量或生物量轉(zhuǎn)換因子模型來獲得[2,4]。根據(jù)Luo等[6]的綜述,1978年至2013年間,我國(guó)學(xué)者已發(fā)表了近200個(gè)樹種的5924個(gè)立木生物量模型。2014年以來,國(guó)家林業(yè)局有計(jì)劃地編制了我國(guó)主要樹種的立木生物量模型,并頒布實(shí)施了系列行業(yè)標(biāo)準(zhǔn)[7-13]。但是,不論是國(guó)外[5,14-20]還是國(guó)內(nèi)[21-28],發(fā)表的林分生物量模型都要顯著少于立木生物量模型。
在已有的林分水平模型中,影響最大的是方精云等[21-22]發(fā)表的21種森林類型的材積源生物量模型,該模型在很多研究中得到了引用[27,29-32]。此外,王斌等[24]利用1266個(gè)不同森林類型樣地的數(shù)據(jù),建立了我國(guó)16種森林類型的生物量與蓄積量之間的雙曲線模型。經(jīng)分析,這些模型存在3個(gè)方面的不足:一是建模樣本較少,大部分模型都是建立在小樣本基礎(chǔ)上。如方精云等[22]建立的21個(gè)模型有18個(gè)(僅落葉松、油松、杉木除外)的建模樣地?cái)?shù)在30 以下,王斌等[24]建立的16個(gè)模型有10個(gè)的建模樣地?cái)?shù)在50 以下。二是建模方法簡(jiǎn)單,基本都是采用普通最小二乘法,未考慮生物量和蓄積量數(shù)據(jù)的異方差性。三是評(píng)價(jià)指標(biāo)單一,僅提供了確定系數(shù)R2[22]或相關(guān)系數(shù)R[24]這一項(xiàng)評(píng)價(jià)指標(biāo),未提供其他誤差方面的評(píng)價(jià)指標(biāo),其適用性存疑。因此,對(duì)林分生物量建模方法做進(jìn)一步研究是非常必要的。
本研究利用我國(guó)3種主要針葉林(落葉松Larixspp. 、油松Pinus tabulaeformisCarr.、杉木Cunninghamia lanceolata(Lamb.) Hook.)的3000個(gè)樣地的地面實(shí)測(cè)數(shù)據(jù),采用加權(quán)回歸估計(jì)[33]和分段建模方法[34],建立林分水平的材積源生物量模型,既為這3種森林類型的生物量調(diào)查提供計(jì)量依據(jù),也為規(guī)范林分生物量建模方法提供科學(xué)參考。
1 數(shù)據(jù)與方法
1.1 數(shù)據(jù)資料
本研究所用數(shù)據(jù)為第九次全國(guó)森林資源清查的固定樣地調(diào)查資料,涉及我國(guó)3種主要的針葉林類型,即:落葉松林、油松林和杉木林。按優(yōu)勢(shì)樹種(占65%以上)確定的這3種類型的針葉林,全國(guó)的有效樣地?cái)?shù)(蓄積量大于0)分別為2490、1185和3152個(gè),每個(gè)樣地都基于每木胸徑測(cè)量數(shù)據(jù),采用一元立木材積模型和立木生物量模型計(jì)算出蓄積量和生物量(包括地上生物量和地下生物量)。由于樣地?cái)?shù)主要集中在每公頃蓄積量和生物量較小的區(qū)段,為了保證所建模型具有廣泛適用性,將全部樣地按每公頃生物量大小用上限排外法分為4級(jí)(<50,50~100,100~150,≧150 t·hm?2),按每級(jí)樣本量盡量均等的原則[35-36]選取建模樣本,每公頃生物量150 t 以上的樣地?cái)?shù)相對(duì)較少,盡可能多選一些用作建模樣本,剩下的樣地作為檢驗(yàn)樣本。經(jīng)綜合考慮,最后確定3種林分類型選取建模樣地分別為1200、800 和1000個(gè)。表1 是3種針葉林分的建模樣地?cái)?shù)和檢驗(yàn)樣地?cái)?shù)按每公頃生物量等級(jí)的分布情況,圖1 是根據(jù)全部3000個(gè)建模樣地?cái)?shù)據(jù)繪制的散點(diǎn)圖。
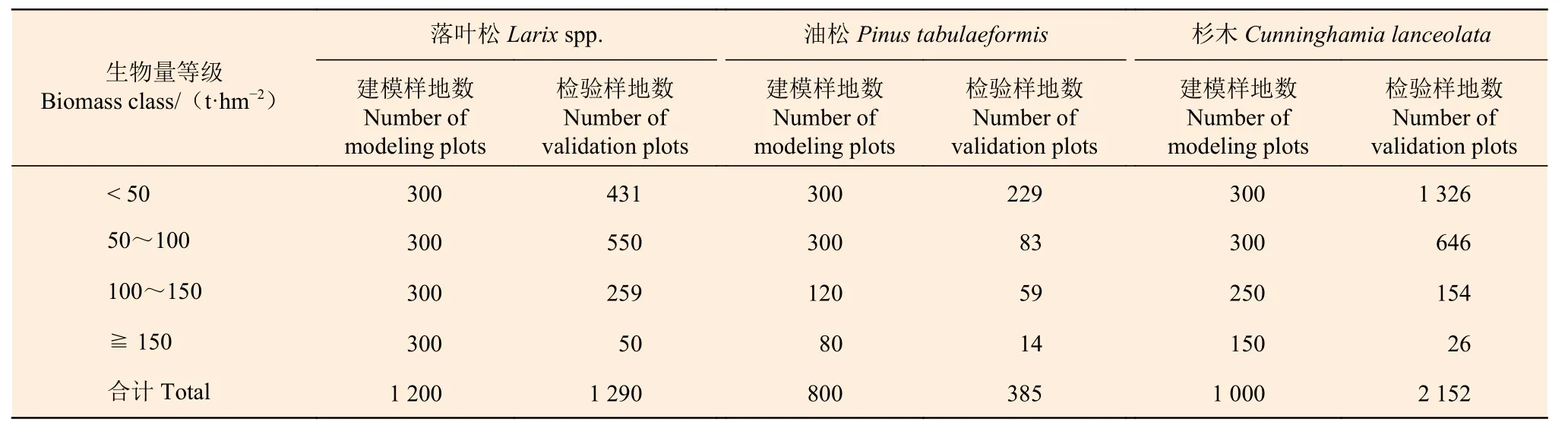
表1 3種針葉林分的建模樣本數(shù)和檢驗(yàn)樣本數(shù)Table 1 The number of modeling plots and validation plots for three coniferous forest types
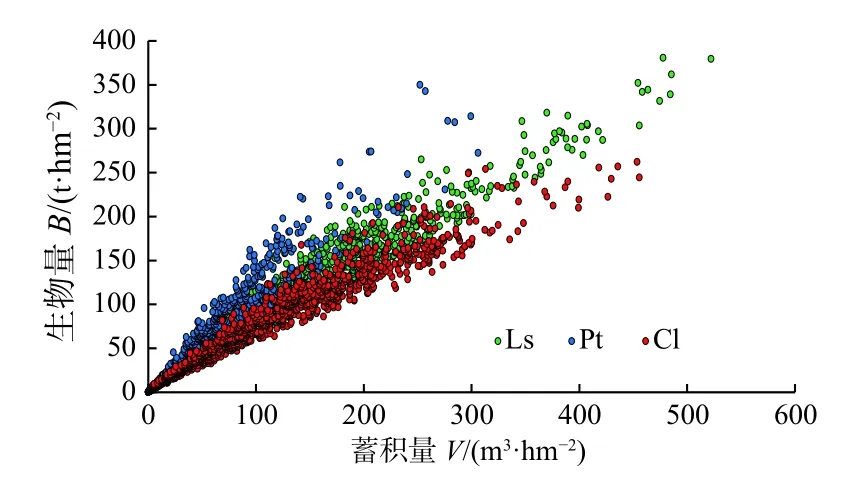
圖1 全部建模樣地生物量與蓄積量散點(diǎn)圖Fig.1 The scatterplot of biomass vs.volume for all modeling plots
1.2 建模方法
將基于前述3種針葉林3000個(gè)樣地的蓄積量、生物量實(shí)測(cè)數(shù)據(jù),首先分別普通回歸和加權(quán)回歸,建立林分生物量模型,并分析其建模效果,最后再用分段建模方法,建立估計(jì)效果更好的生物量模型。
1.2.1 回歸估計(jì)方法 林分生物量主要與林分蓄積量有關(guān),基于蓄積量的生物量模型應(yīng)用最為廣泛[21-22,24,27,29-32]。根據(jù)方精云等[22]對(duì)全國(guó)21種森林類型的研究結(jié)果,林分生物量與蓄積量之間呈線性相關(guān)。從3000個(gè)樣地的每公頃生物量與蓄積量數(shù)據(jù)的散點(diǎn)圖分析,這種線性相關(guān)規(guī)律也是非常明顯的(圖1)。因此,本研究確定采用如下線性形式的林分生物量模型:

式中:B為每公頃生物量(t·hm?2),V為每公頃蓄積量(m3·hm?2),a0、b0為模型參數(shù),ε1為誤差項(xiàng),假定其服從均值為0 的正態(tài)分布。將(1)式兩邊除以V,可得到如下林分生物量轉(zhuǎn)換因子模型:
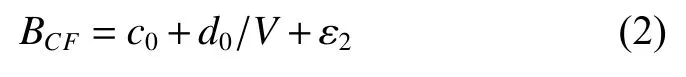
式中:BCF為生物量轉(zhuǎn)換因子(=B/V),c0、d0為模型參數(shù),ε2為誤差項(xiàng)。式(2)為非線性模型,如果設(shè)定y=BCF,x= 1/V,則可以轉(zhuǎn)為以下線性模型:

上述模型(1)、(3)的參數(shù)可采用普通線性回歸估計(jì)方法求解。根據(jù)對(duì)模型的結(jié)構(gòu)分析,模型參數(shù)之間理論上應(yīng)該存在以下關(guān)系:

事實(shí)上,模型(2)、(3)的擬合結(jié)果,就相當(dāng)于模型(1)的加權(quán)回歸結(jié)果,其權(quán)函數(shù)為w=1/V。因此,根據(jù)實(shí)際的擬合結(jié)果,式(4)必然是不成立的。由于生物量數(shù)據(jù)與蓄積量數(shù)據(jù)類似,都具有異方差性,模型(1)應(yīng)該采用加權(quán)回歸估計(jì)才是合適的[33,37]。參照有關(guān)權(quán)函數(shù)的研究結(jié)論[37],權(quán)函數(shù)w= 1/V效果不一定最好,更通用的權(quán)函數(shù)應(yīng)為w= 1/Vk,其中k一般在0.5~1.0 之間。
為了區(qū)別,這里將生物量模型(1)的擬合方法稱為普通回歸,生物量轉(zhuǎn)換因子模型(2)或(3)的擬合方法稱為加權(quán)回歸1(權(quán)函數(shù)w1=1/V),以模型(1)為基礎(chǔ)進(jìn)行的加權(quán)回歸估計(jì)方法稱為加權(quán)回歸2(權(quán)函數(shù)w2= 1/Vk)。
1.2.2 分段建模方法 當(dāng)變量的取值范圍很大時(shí),用一個(gè)模型通常難以對(duì)各個(gè)區(qū)段都作出準(zhǔn)確估計(jì),解決這一問題的有效方法就是分段建模。在建立單木水平的生物量模型時(shí),就已經(jīng)有人用到了這一方法[34]。林分生物量的建立,同樣可能碰到這一問題。假設(shè)最小的區(qū)段(如每公頃蓄積量50 m3·hm?2以下)存在明顯偏估,就可以將自變量V=50 m3·hm?2置為兩個(gè)模型的鏈接點(diǎn),并將適用于V<50 m3·hm?2的模型參數(shù)設(shè)定為a1和b1,適用于V≧50 m3·hm?2的模型參數(shù)設(shè)定為a2和b2。為了保證兩個(gè)模型在鏈接點(diǎn)的估計(jì)值一致,先擬合其中一個(gè)模型的2個(gè)參數(shù)后,另一個(gè)模型2個(gè)參數(shù)的估計(jì)就要受到這一條件的約束,其中只有一個(gè)參數(shù)是獨(dú)立估計(jì)的,另一個(gè)參數(shù)直接根據(jù)(5)式由其他3個(gè)參數(shù)推出。
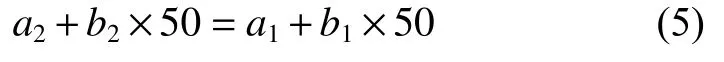
根據(jù)兩個(gè)分段模型擬合的先后順序,可以得出2 組分段模型:
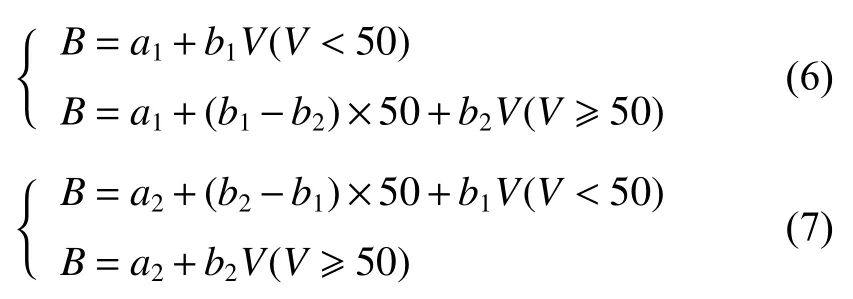
式(6)是先擬合適用于V<50 m3·hm?2的模型參數(shù)a1和b1,再擬合適用于V≧50 m3·hm?2的模型;式(7)是先擬合適用于V≧50 m3·hm?2的模型參數(shù)a2和b2,再擬合適用于V<50 m3·hm?2的模型。通過對(duì)比其評(píng)價(jià)指標(biāo)的優(yōu)劣,選定擬合效果較好的模型。
1.2.3 模型評(píng)價(jià)方法 用于模型評(píng)價(jià)的指標(biāo)包括以下6 項(xiàng):確定系數(shù)R2、估計(jì)值的標(biāo)準(zhǔn)差(也稱剩余標(biāo)準(zhǔn)差)SEE、總體相對(duì)誤差TRE、平均系統(tǒng)誤差A(yù)SE、平均預(yù)估誤差MPE和平均百分標(biāo)準(zhǔn)誤差MPSE[38-39]。其中MPE和MPSE的計(jì)算公式如下:
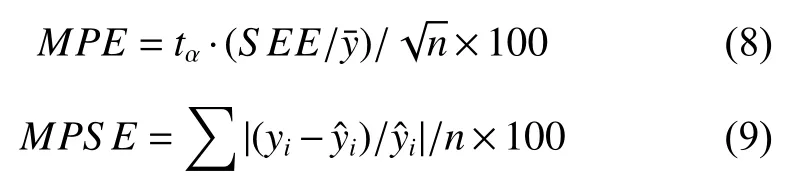
式中:yi為實(shí)際調(diào)查值,為模型預(yù)估值,為樣本平均值,n 為樣地?cái)?shù),tα為置信水平α 時(shí)的t 值。對(duì)建立的回歸模型,計(jì)算以上6 項(xiàng)指標(biāo)值,根據(jù)指標(biāo)大小進(jìn)行模型評(píng)價(jià)。
從實(shí)用性角度考慮,一般要求模型的TRE和ASE均在 ± 3%以內(nèi),MPE小于3%,MPSE小于15%。另外,殘差圖也是評(píng)價(jià)模型的重要參考依據(jù)。一個(gè)好的模型,殘差應(yīng)當(dāng)呈隨機(jī)分布。也就是說,模型每個(gè)區(qū)段的總體相對(duì)誤差TRE都應(yīng)該相差不大,一般應(yīng)在 ± 5%以內(nèi)。為了評(píng)價(jià)模型的廣泛適用性,還采用檢驗(yàn)樣本進(jìn)行獨(dú)立交叉檢驗(yàn),計(jì)算模型的總體相對(duì)誤差TRE是否在允許誤差范圍內(nèi)。
2 結(jié)果與分析
利用3種針葉林的3000個(gè)樣地的每公頃蓄積量和生物量數(shù)據(jù),分別采用普通回歸、加權(quán)回歸1(權(quán)函數(shù)w1= 1/V)和加權(quán)回歸2(權(quán)函數(shù)w2=1/Vk)擬合線性生物量模型(1),其擬合結(jié)果和評(píng)價(jià)指標(biāo)見表2。
從表2 可以明顯看出,不論是2個(gè)參數(shù)的估計(jì)值還是6 項(xiàng)評(píng)價(jià)指標(biāo),加權(quán)回歸2 的結(jié)果都居于普通回歸和加權(quán)回歸1 之間,且更接近加權(quán)回歸1 的結(jié)果,唯有TRE和ASE這2 項(xiàng)指標(biāo)比較特殊:普通回歸TRE為0,ASE較大;加權(quán)回歸1 則ASE接近于0,TRE較大;而加權(quán)回歸2 則處于折中狀態(tài),TRE和ASE都與0 相差不大,盡可能同時(shí)控制在預(yù)定的誤差范圍內(nèi)(如 ± 3%以內(nèi))。盡管從R2、SEE和MPE這3 項(xiàng)指標(biāo)看,普通回歸模型要好些,但從ASE和MPSE看,則普通回歸模型要顯著差些。最后,再來看另外一項(xiàng)重要指標(biāo)總體相對(duì)誤差TRE,為了更深入了解模型在不同生物量等級(jí)的擬合效果,表3 分別落葉松、油松和杉木按建模樣本和檢驗(yàn)樣本列出了總體和各個(gè)生物量等級(jí)的TRE。
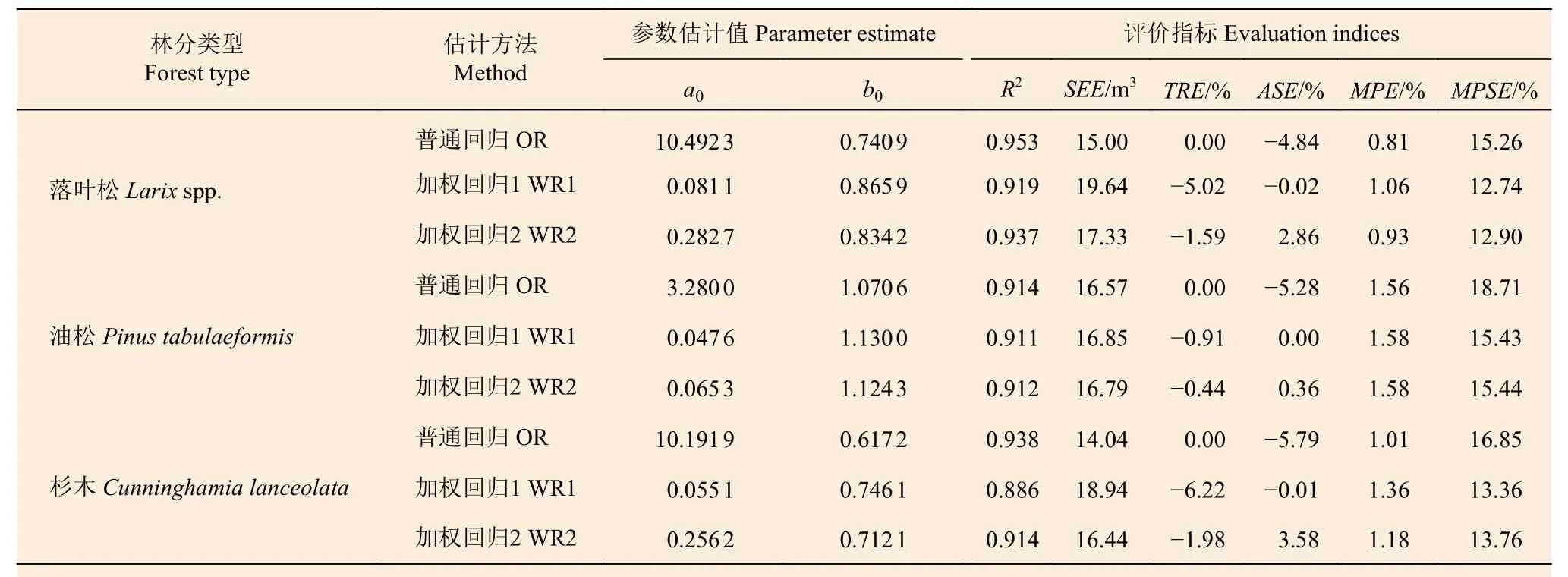
表2 林分生物量模型的參數(shù)估計(jì)值和模型評(píng)價(jià)指標(biāo)Table 2 The parameter estimates and evaluation indices of stand-level biomass models
從表3 可以看出,不論是考慮建模樣本還是檢驗(yàn)樣本,加權(quán)回歸模型的結(jié)果都要優(yōu)于普通回歸模型,而加權(quán)回歸模型2 又要略優(yōu)于加權(quán)回歸模型1。因此,從模型本身特性、6 項(xiàng)評(píng)價(jià)指標(biāo)及獨(dú)立檢驗(yàn)結(jié)果綜合考慮,應(yīng)當(dāng)采用加權(quán)回歸模型2 的擬合結(jié)果。
然而,如果再仔細(xì)查看表3 中加權(quán)回歸模型2 在各個(gè)生物量等級(jí)的TRE(加粗的部分),發(fā)現(xiàn)還是存在一些不足,如:生物量小的區(qū)段總體上表現(xiàn)為正偏,而生物量大的區(qū)段總體上表現(xiàn)為負(fù)偏(油松相反);部分區(qū)段TRE較大,超出了 ± 5%的范疇。根據(jù)對(duì)殘差圖所作的分析,生物量小的區(qū)段容易出現(xiàn)較大偏差,因此,如果采用分段建模方法,應(yīng)該能提高預(yù)估精度。綜合考慮樣本量的支撐程度和規(guī)范統(tǒng)一性,本研究將自變量V= 50 m3·hm?2設(shè)置為分段建模的鏈接點(diǎn),同時(shí)建立了式(6)和式(7)兩套模型,擬合結(jié)果見表4,基于建模樣本和檢驗(yàn)樣本計(jì)算的各個(gè)生物量等級(jí)的總體相對(duì)誤差TRE見表5。
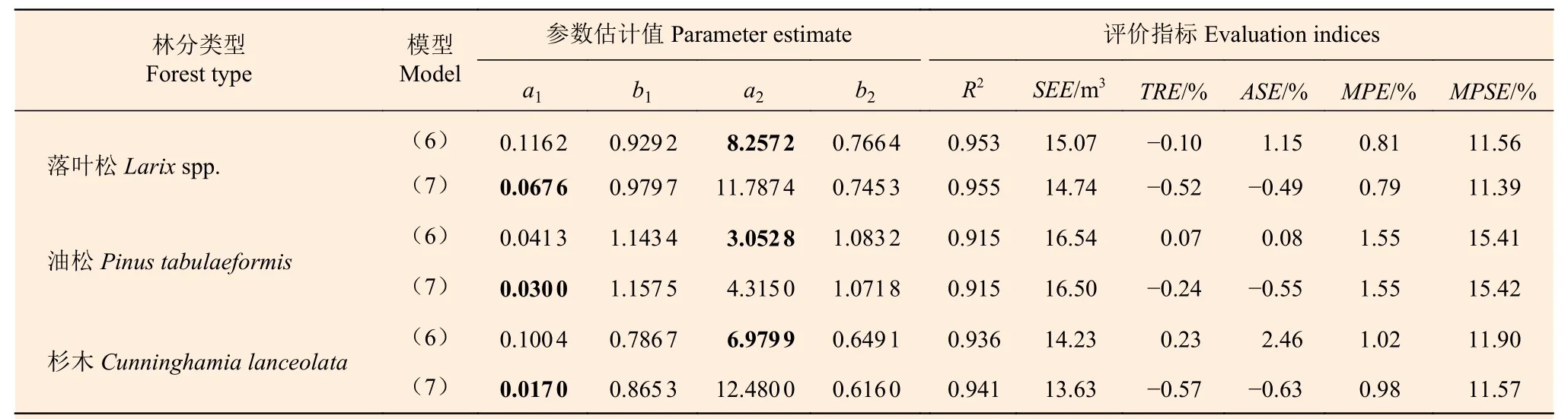
表4 分段建模的參數(shù)估計(jì)值和模型評(píng)價(jià)指標(biāo)Table 4 The parameter estimates and evaluation indices of segmented biomass models
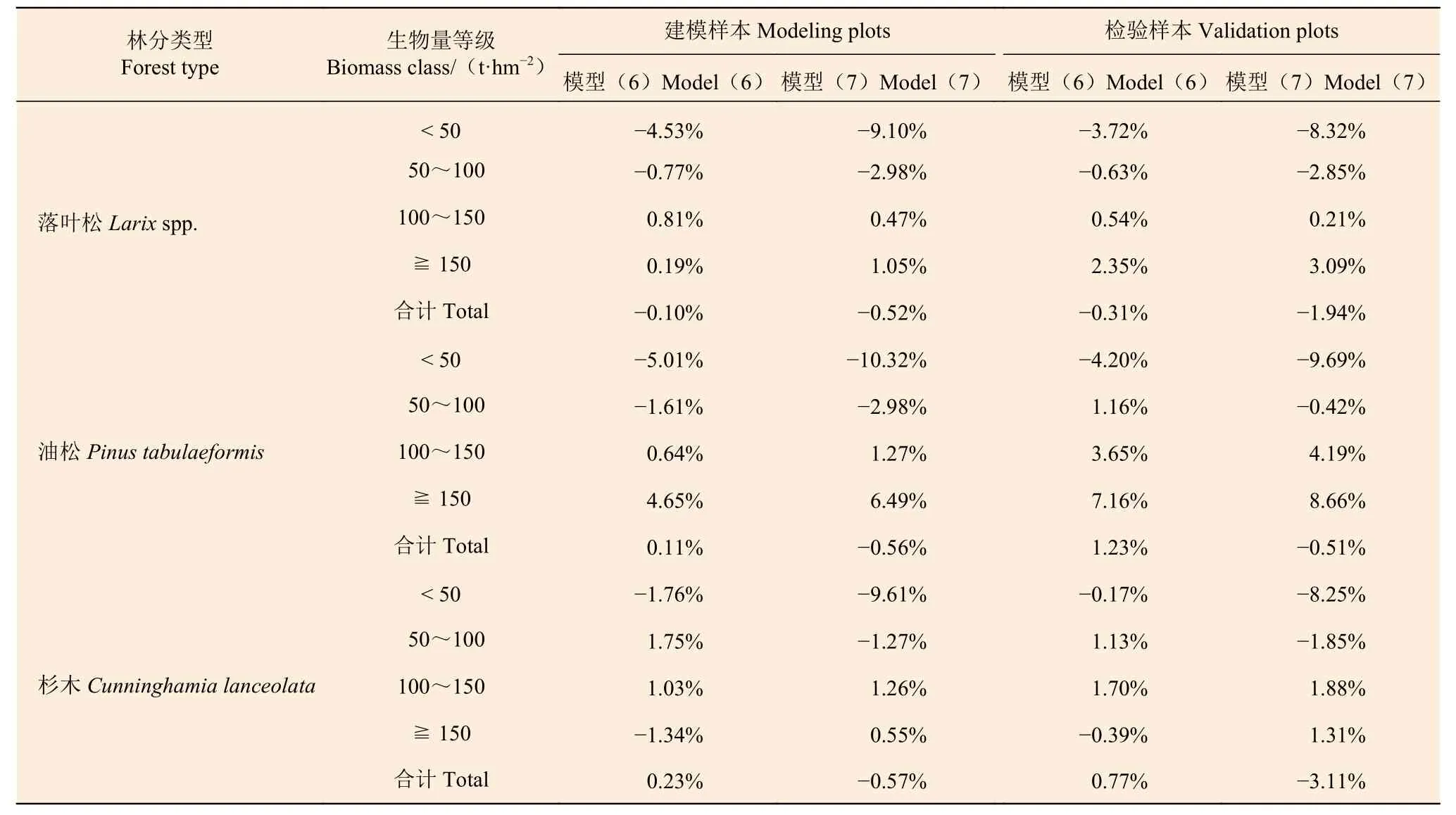
表5 分段生物量模型的總體相對(duì)誤差Table 5 The total relative errors of segmented biomass models
從表4 的6 項(xiàng)評(píng)價(jià)指標(biāo)看,模型(6)和(7)之間的差異不明顯;但從表5 的對(duì)比可以看出,模型(6)明顯優(yōu)于模型(7),每個(gè)生物量等級(jí)的誤差基本都在 ± 5%以內(nèi)。除油松的分段模型改進(jìn)甚微外,落葉松和杉木的分段模型有顯著改進(jìn),杉木分段模型各生物量等級(jí)的誤差甚至達(dá)到了 ± 2%以內(nèi)。因此,綜合考慮模型的各項(xiàng)評(píng)價(jià)指標(biāo)及檢驗(yàn)結(jié)果,最終選定分段模型(6)作為3種針葉林分的生物量估計(jì)模型。
3 討論
本研究針對(duì)我國(guó)在林分生物量建模方面存在的樣本數(shù)量偏少、建模方法簡(jiǎn)單、評(píng)價(jià)指標(biāo)單一等問題,基于第九次全國(guó)森林資源清查3000個(gè)固定樣地的實(shí)測(cè)數(shù)據(jù),綜合利用加權(quán)回歸方法和分段建模方法,建立了落葉松、油松、杉木3種主要針葉林的每公頃生物量模型。最終確定的分段回歸模型如下:

其確定系數(shù)R2在0.915~0.953 之間,平均預(yù)估誤差MPE在0.81%~1.55% 之間,平均百分標(biāo)準(zhǔn)誤差MPSE在11.56%~15.41%之間。林分生物量與蓄積量呈線性相關(guān),這與方精云等[22]的研究結(jié)論是一致的。但是,由于在樣本數(shù)量、建模方法等方面存在的差異,模型的適用性肯定會(huì)有很大不同。在引言中提到方精云等[22]建立的21個(gè)林分類型的生物量模型,建模樣本數(shù)量在30 以上的僅有以下3個(gè)模型:
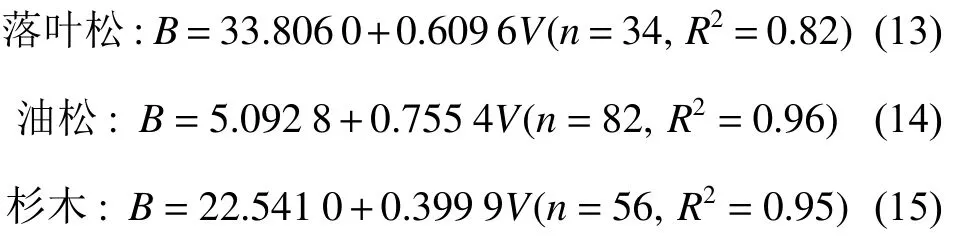
表6 列出了利用本研究所收集的全部樣地對(duì)這3個(gè)模型的檢驗(yàn)結(jié)果。可以看出,3個(gè)模型不僅總體的TRE遠(yuǎn)遠(yuǎn)超出了允許誤差范圍,不同生物量等級(jí)的估計(jì)值更是存在非常大的系統(tǒng)偏差。通過與本研究所建模型參數(shù)進(jìn)行對(duì)比,發(fā)現(xiàn)式(13)~(15)的截距參數(shù)都要偏大,而斜率參數(shù)都要偏小,這正是對(duì)蓄積量小的樣地會(huì)產(chǎn)生正偏而對(duì)蓄積量大的樣地會(huì)產(chǎn)生負(fù)偏的直接原因。之所以其參數(shù)估計(jì)值出現(xiàn)大的偏差,主要原因應(yīng)該是參數(shù)估計(jì)方法不恰當(dāng),采用的是普通回歸而不是加權(quán)回歸。其次,樣本量的大小及樣本結(jié)構(gòu)的好壞也是影響因素之一。筆者曾試圖系統(tǒng)抽取表1 中全部樣本的2/3 建模、1/3 檢驗(yàn),盡管建模樣本數(shù)量大幅增加,但因?yàn)闃颖窘Y(jié)構(gòu)不理想,建模結(jié)果并未達(dá)到預(yù)期要求。因此,建模成功的要素,一是樣本數(shù)量足夠;二是樣本結(jié)構(gòu)合理;三是建模方法科學(xué)。表6 也列出了利用全部樣本對(duì)本研究所建模型的檢驗(yàn)結(jié)果,總相對(duì)誤差都在 ± 1%以內(nèi),各個(gè)生物量等級(jí)的估計(jì)誤差大都在 ± 5%以內(nèi),最大的也未超出 ± 10%的范圍。這樣的模型,才是適用性廣的模型。
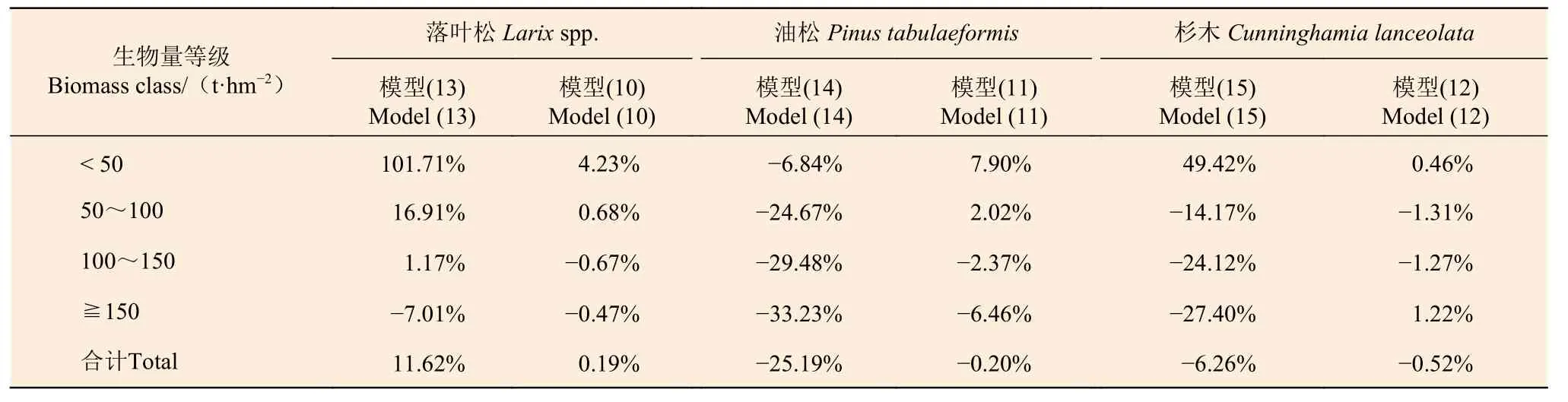
表6 不同生物量模型總體相對(duì)誤差的對(duì)比Table 6 The comparison of total relative errors of different biomass models
圖2 展示了落葉松生物量模型(10)和模型(13)的殘差分布,可以看出,因?yàn)槟P停?3)的截距參數(shù)a0= 33.8060,會(huì)得出每公頃蓄積量為0 的落葉松林其生物量高達(dá)33.8 t·hm?2的結(jié)果,從而導(dǎo)致每公頃蓄積量較小的林分,其生物量估計(jì)結(jié)果出現(xiàn)正偏;每公頃蓄積量較大的林分,其生物量估計(jì)結(jié)果出現(xiàn)負(fù)偏。其他2個(gè)樹種的生物量模型(11)、(12)與模型(14)、(15)的殘差分布對(duì)比情況也類似,為省篇幅,不再列出。
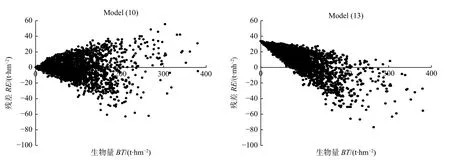
圖2 落葉松生物量模型(10)和模型(13)的殘差分布對(duì)比Fig.2 Comparison of residual errors between model (10) and (13) for larch
4 結(jié)論
根據(jù)本研究的相關(guān)結(jié)果,可以得出以下結(jié)論:(1)林分每公頃生物量與蓄積量呈線性相關(guān)。(2)建立林分生物量模型,應(yīng)當(dāng)采用加權(quán)回歸方法;當(dāng)一個(gè)模型難以準(zhǔn)確估計(jì)各個(gè)等級(jí)的生物量時(shí),可以采用分段建模方法。(3)樣本數(shù)量和樣本結(jié)構(gòu)是除建模方法之外影響建模效果的另外兩個(gè)重要因素。(4)本研究所建3種針葉林的生物量模型,預(yù)估精度高,可以在實(shí)踐中推廣應(yīng)用。
最后需要補(bǔ)充的一點(diǎn)是,本研究只是基于優(yōu)勢(shì)樹種劃分的林分類型分別建立材積源生物量模型,沒有再分樹種組成按絕對(duì)純林(占90%以上)和相對(duì)純林(占65%~90%)分別建模,也沒有分起源按天然林和人工林分別建模。因此,用于預(yù)估更細(xì)的類型時(shí)模型的誤差肯定會(huì)有所增加。若想進(jìn)一步提高模型的預(yù)估精度,可以分別天然林、人工林和絕對(duì)純林、相對(duì)純林建模,或?qū)⑵鹪础⒓兞诸愋偷纫蜃影磫∽兞繉?duì)待,建立適應(yīng)性更廣的啞變量模型。另外,本研究所建材積源生物量模型是以立木生物量模型的估計(jì)結(jié)果為基礎(chǔ)建立的,屬于林分水平的模型;與單木水平的模型相比,其預(yù)估精度要略低[40-41]。模型應(yīng)用時(shí),若具備單木水平模型的應(yīng)用條件,應(yīng)該首先采用單木模型;若只有樣地、林分或小班水平的數(shù)據(jù),不具備單木水平模型的應(yīng)用條件,才考慮采用林分水平模型。

