風浪聯合下導管架式風機結構疲勞特性研究

常卡,王坤鵬

（江蘇科技大學船舶與海洋工程學院，江蘇鎮江 212003）

0 引言

隨著海上風電技術的成熟，海上風能資源受到越來越多的關注，陸上風電產業逐漸轉向海洋，并從近海往深海發展[1]，[2]。相對于陸上風機，海上風電處于復雜的海洋環境中，長期受到空氣動力荷載與水動力荷載等動態荷載聯合作用，風機結構本身的動力特性反應變得更為復雜，易對結構造成嚴重的疲勞破壞[3]。

為了保證風機結構能夠在服役期間正常工作，對風機基礎結構進行準確的疲勞分析是必要的。秦培江[4]利用譜分析法結合多輸入線性系統理論研究了導管架式海上風機支撐結構在風浪聯合作用下的疲勞特性。Yeter B[5]考慮了風機運行模式，運用簡化譜分析方法對三腳架式海上風機支撐結構在風和波浪荷載作用下的疲勞損傷進行了評估，并對基礎結構進行了優化設計。Marino E[6]基于氣彈-水動-伺服-彈性整體耦合模型開展了在不同波浪模型和不同湍流強度下的單樁風機塔筒底部疲勞特性研究。Ziegler L[7]提出了一種有效的頻域方法來計算波浪對海上風機單樁基礎的疲勞載荷，同時還說明水深、土壤剛度、波浪高度和波浪周期等參數對疲勞載荷的重要性。Wei K[8]研究了規則波和不規則波荷載對導管架式海上風電機組結構動力響應的影響。MoratóA[9]基于全局耦合模型對單樁風機在IEC61400-3規范的極限狀態荷載工況下的動力響應與基礎結構疲勞承載力進行了校核。

本文以NREL 5 MW風機為例，采用FAST軟件[10]建立導管架式風機氣動-控制-結構彈性-水動力全耦合模型。首先，基于整體耦合模型分析整機一階模態；其次，研究共振對結構的危害，風浪異向對結構疲勞損傷的影響；最后，基于風機正常發電狀態采用雨流計數法開展長期風浪分布下的基礎關鍵管節點和塔筒底端疲勞可靠性研究，并將應力疊加法和疲勞疊加法與風浪耦合下的結構損傷預報結果相比較。研究結果可為導管架式風機疲勞承載力校核提供參考。

1 風機系統參數

本文采用的NREL 5 MW導管架式風電機組的結構模型如圖1所示。

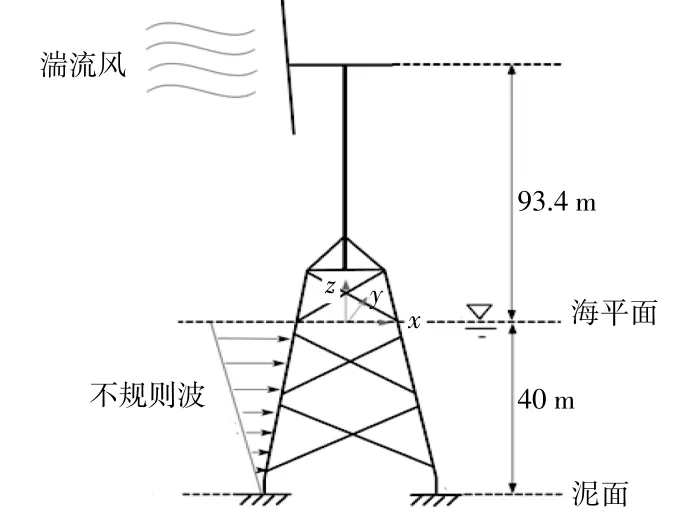
圖1 導管架式風機Fig.1 Jacket-type wind turbine

該風電機組轉子直徑為126 m，輪轂位于平均海平面上方93.4 m處，工作海域水深為40 m，塔筒為多段變截面空心圓柱結構。文獻[11]詳細介紹了NREL 5 MW風電機組和塔筒的參數。風機支撐基礎選擇導管架結構形式，導管架的每個立面都有3個X形支撐管，采用兩個節點梁單元來表示導管架模型。

圖2為本文的風機基礎模型，導管架4根腿與樁連接。

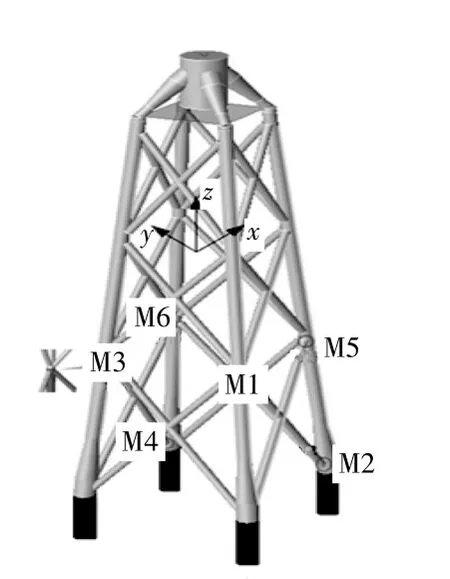
圖2 風機基礎模型Fig.2 Wind turbine foundation model

本文側重研究導管架的疲勞特性，故將樁腿在泥面處簡化為固支約束。圖中：M1～M6為基礎結構撐管與主管相交管節點，圓圈處是疲勞評估的關鍵位置。導管架基礎相關參數見表1。

表1 導管架基礎模型尺寸Table 1 Dimensions of jacket foundation model m

2 環境荷載研究理論

2.1 風機系統運動方程

在FAST軟件中，采用多體和模態動力學相結合的方法來對塔筒和風電機組組成的系統進行模擬。充分考慮環境荷載、控制系統與風機結構之間的相互作用，風機系統的運動方程為

FAST軟件可模擬海上風機的基礎結構，并在基礎與塔筒交界面處進行數據交互。在每一步分析中，FAST軟件將基礎頂端的內力傳輸給塔筒底端，完成塔筒和風電機組系統的動力分析，然后將塔筒底端的位移、速度和加速度傳輸給基礎頂端，完成基礎的動力響應分析。

2.2 空氣動力荷載

葉素-動量理論是葉素理論與動量理論相結合的一種求解空氣動力載荷的迭代方法。葉素理論將作用在葉片上的總力當作作用在離散葉片單元上力的疊加之和。動量理論將徑向葉片單元截面的動量損失與氣流產生的局部軸向力相關聯。根據葉素-動量理論可求出葉輪總推力T和扭矩Q分別為

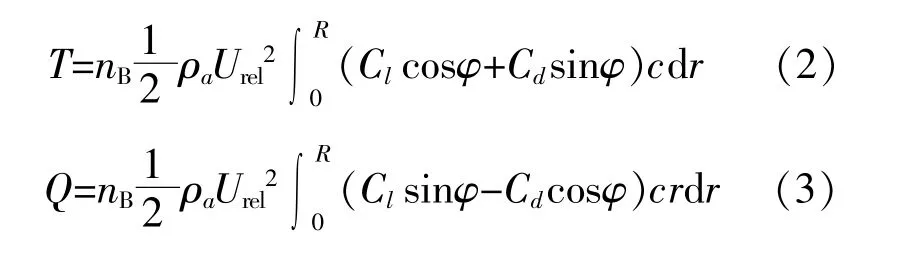
式中：Cl為升力系數；Cd為阻力系數；φ為入流角；nB為風機葉片數量；Urel為相對風速；c為弦長；r為葉素到輪轂中心的距離；R為葉片半徑。

2.3 波浪荷載

對于海洋工程結構中的細長桿件，采用半經驗半理論公式的莫里森方程計算作用于結構的波浪力（拖曳力和慣性力）。

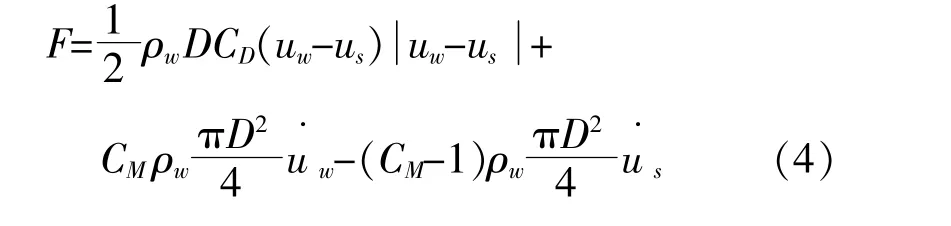
式中：CD為拖曳力系數；CM為慣性力系數；ρw為海水密度；D為結構直徑；uw為流體質點速度；us為結構速度；u·w為流體加速度；u·s為結構加速度。

3 數值研究與結果分析

3.1 風機整體模態

基于整體耦合模型研究簡諧波作用下的塔頂運動響應。波浪頻率為0.2～0.5 Hz，分析22個簡諧波頻率，波浪方向沿x軸正方向。塔頂的位移和加速度的幅值曲線如圖3所示。由圖3可知，塔頂的位移和加速度的運動響應幅值在頻率為0.309 9 Hz時最大，塔頂x方向的位移和加速度最大值分別為0.204 9 m和1.306 m/s2。根據塔頂的位移和加速度的RAO曲線可確定結構的固有頻率為0.309 9 Hz。

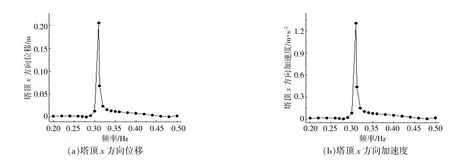
圖3 塔頂運動響應Fig.3 Tower top motion response

考慮到風機1P（P為葉輪切入轉速6.9 r/min至額定轉速12.1 r/min的范圍）和3P旋轉頻率的影響，得到風機結構安全裕度區間（圖4）。由于風機結構的各種不確定因素，充分擴大5%的設計裕度區域，可求得風機結構固有頻率應在0.213～0.328 Hz。風機結構固有頻率為0.309 9 Hz，位于圖4所示的安全區域，可初步判斷導管架結構符合整機頻率設計要求。

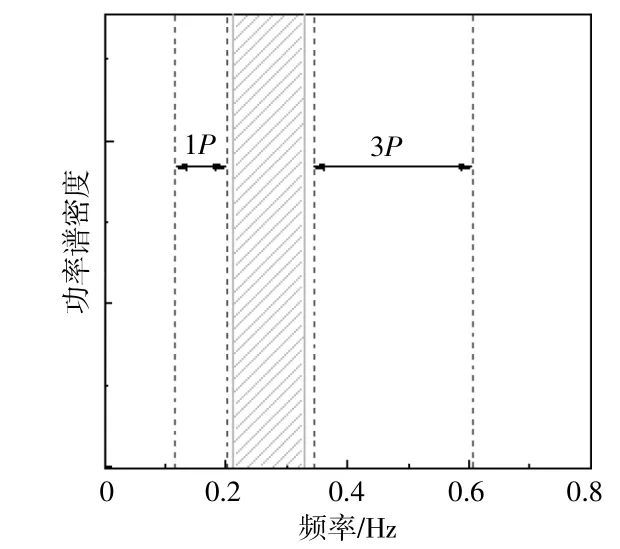
圖4 結構安全裕度區間Fig.4 Margin of safety for structure

3.2 風機基礎疲勞分析

3.2.1 疲勞分析方法

對導管架基礎關鍵管節點（M1～M6）和塔筒底端（TB）進行疲勞損傷分析，采用DNV-RPC203規范[12]建議的公式求管節點應力和應力集中因子SCF，選擇海水中D級受陰極保護的雙斜率S-N曲線，結合雨流計數法和Miner線性疲勞累積損傷理論求短期海況疲勞損傷。

式中：D為疲勞損傷累積值；ni為應力范圍Δσi的實際循環次數；Ni為應力范圍Δσi下結構達到破環時的循環作用次數；N為循環應力級數。

荷載的長期分布為所有荷載下的單個短期應力響應分布與每個荷載相對出現概率的加權和。風機結構在長期荷載下總的疲勞損傷Dt為

式中：Di為第i個短期荷載疲勞損傷累積值；Pi為第i個短期荷載出現的概率；k短期荷載個數。

3.2.2 共振對風機結構的影響

采用FAST軟件研究共振對風機結構疲勞損傷的影響。本文環境條件為IEC61400-3[13]規定的正常湍流風和正常海況，三維湍流風選用Kaimal譜模擬，隨機波浪選擇P-M譜模擬，模擬時長為600 s。選取兩種環境工況計算單獨波浪和風浪耦合下的結構關鍵位置和塔筒底端的疲勞損傷。設計環境條件Ⅰ：Vw=6 m/s，Hs=0.5 m，Tp=3.225 s；環境條件Ⅱ：Vw=6 m/s，Hs=0.5 m，Tp=10 s；風浪方向均沿x軸正方向。

圖5和圖6分別為單獨波浪和風浪耦合在兩種環境工況下的疲勞損傷貢獻。

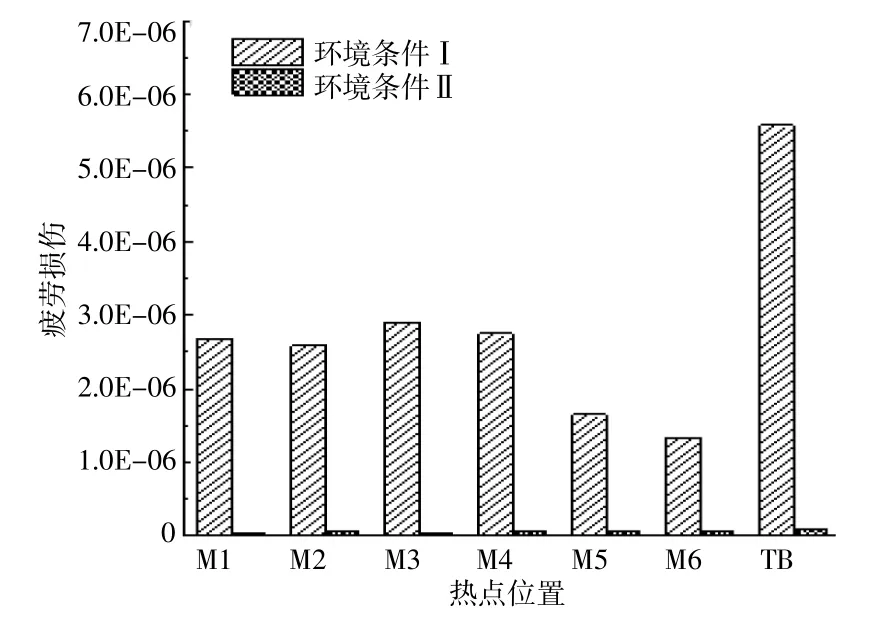
圖5 熱點疲勞損傷(單獨波浪)Fig.5 Fatigue damage of hot spots（wave only）

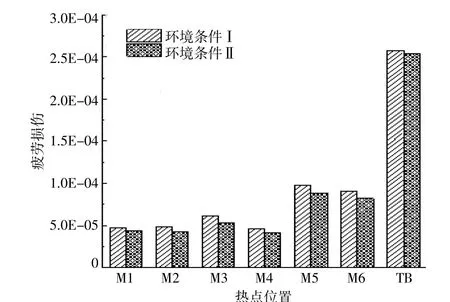
圖6 熱點疲勞損傷(風浪聯合)Fig.6 Fatigue damage of hot spots（combination of wind and wave）

由圖5和圖6可知，在環境條件Ⅰ下，單獨波浪和風浪耦合對熱點位置的疲勞損傷要高于環境條件Ⅱ下的疲勞損傷。原因可能是環境條件Ⅰ的波浪頻率為整機一階模態頻率，會引起結構共振產生更大能量，從而加速結構的損壞。在環境條件Ⅰ作用下，風浪耦合引起熱點位置的疲勞損傷遠大于單獨波浪下的疲勞損傷。這說明，盡管隨機波的譜峰周期為共振頻率對應的周期，但波浪引起的損傷遠小于風載荷導致的損傷。出現這一現象的主要原因是，對于導管架式風機，即便譜峰周期對應于整機一階模態的周期，隨機波浪也很難引起風機系統的明顯共振。

圖7所示為不同波浪模型下的塔頂位移響應。簡諧波的波高和周期分別等于隨機波的有義波高和譜峰周期，周期等于整機一階模態周期，從塔頂運動來看，后者引起的響應明顯小于前者。

3.2.3 風浪異向對疲勞損傷影響

DNV建議，對海上風機進行疲勞分析時須要考慮風浪方向對疲勞損傷的作用。本文風方向始終沿x軸正方向，通過改變波浪的方位角度達到風浪異向的效果。波浪方向設置為兩組，與x軸正方向夾角分別為30 °和60 °。基于環境條件Ⅰ和Ⅱ開展風浪耦合在風浪異向下的疲勞損傷，并與風浪同向的疲勞損傷結果相比較。圖8為環境條件Ⅰ，Ⅱ下熱點位置在不同波浪方位角度的疲勞損傷。

由圖8可知：風浪耦合效應對塔筒底端疲勞損傷的影響要高于基礎管節點的損傷，對于同一方向的波浪來說，環境條件Ⅰ對熱點位置的疲勞損傷貢獻比環境條件Ⅱ稍大；風浪荷載方向存在錯位時，熱點位置的疲勞損傷值存在差異；在環境條件Ⅱ下，基礎管節點和塔筒底端的疲勞損傷在不同波浪方位角度下的變化趨勢基本相同，而環境條件Ⅰ下管節點M1～M4的疲勞損傷與M5，M6和塔筒底端的疲勞損傷在不同波浪方位角度下的變化趨勢相反。整體來說，風浪同向時，熱點位置的疲勞損傷最小，隨著風浪方向錯位角度的增大，疲勞損傷會增加。原因可能是，隨著風浪錯位角度的增大，波浪荷載方向上的氣動阻尼逐漸減小，使得風波聯合荷載相對較大，從而造成結構疲勞累積損傷增大。

3.2.4 長期風浪分布下的疲勞損傷

針對長期風浪分布下的撐管與主管交界管節點和塔筒底部有效可靠性開展研究。所處海域選為北大西洋某區域。以IEC61400-3規范[13]中風機正常運行狀態作為疲勞分析工況。實際工程中，海上風機的疲勞損傷仿真工況非常多，本文簡化計算，結合北大西洋風浪分布資料，按照文獻[13]的要求，在切入風速和切出風速之間選擇5組風速、4組有義波高和4組譜峰周期（表2）進行隨機組合，風速、波高和周期共合成80組疲勞工況，所有工況的概率密度之和為99.91%。

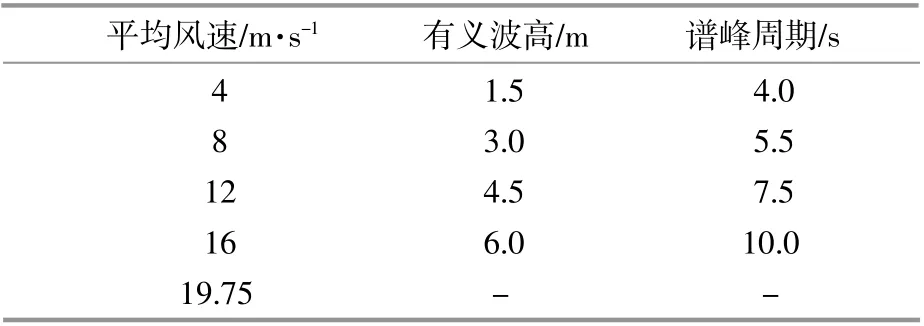
表2 疲勞工況參數Table 2 Fatigue case parameters

單獨計算風荷載和波浪荷載下的響應，然后采用應力疊加或者疲勞損傷疊加的方法計算風浪產生的疲勞損傷度，可以減少兩者組合產生的大量工況，能極大地縮短計算時間。下面通過將這兩種方法預報的疲勞損傷與全耦合方法預報的結果進行對比，分析這兩種方法的準確性。

圖9為結合每組疲勞工況對應的概率，采用不同疲勞疊加方法得到熱點位置的年疲勞累積損傷值與風浪耦合預報結果的比較。

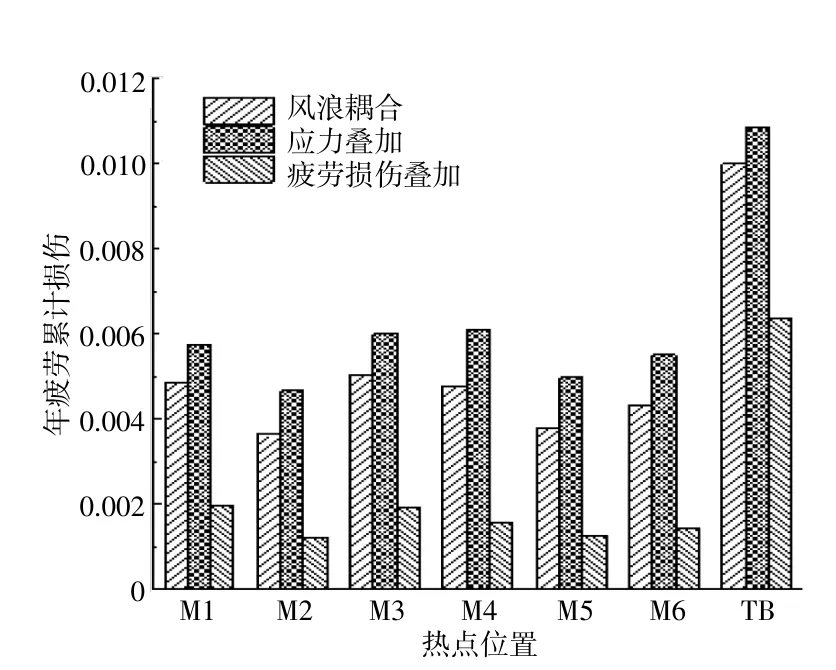
圖9 熱點年疲勞累積損傷Fig.9 Fatigue cumulative damage of hot spots

由圖9可知：風浪耦合下的管節點和塔筒底端的年疲勞損傷值介于應力疊加法和疲勞損傷疊加法的結果之間，塔筒底端的年損傷值大于基礎管節點的年損傷；對于塔筒底端，應力疊加法的年損傷累積值是風浪耦合結果的1.09倍；對于基礎管節點，M3位置的疲勞損傷與M1和M4的疲勞損傷值很相近，與風浪耦合下的預報結果相比較，M1，M3和M4位置應力疊加的損傷累積值的最大誤差分別為18%，19%和25%。導致上述結果的原因可能是，應力疊加法忽略了風浪聯合下氣動阻尼的影響，整體來說，風浪疲勞損傷疊加方法會嚴重低估結構的疲勞損傷，應力疊加法與風浪耦合所產生的疲勞累積損傷較為相近，且預報結果偏保守。由于單獨計算風荷載和波浪荷載下的響應能極大地縮短計算時間，因此可在初步設計時使用應力疊加方法進行結構疲勞評估。

4 結論

本文以導管架式風機為研究對象，采用FAST軟件建立海上風機系統全耦合模型。首先基于整體耦合模型通過簡諧波激發的塔筒響應分析風機的一階模態；其次，研究共振和風浪異向對結構疲勞損傷的影響；最后，基于風機正常發電狀態，采用雨流計數法開展長期風浪分布下的基礎關鍵管節點和塔筒底端疲勞損傷研究，并將應力疊加法和疲勞疊加法與風浪耦合下的結構損傷預報結果相比較，得到以下結論。

①波浪的譜峰周期對應于整機一階模態的周期，隨機波難以引起風機明顯的共振響應。

②風機載荷對導管架基礎和塔筒疲勞損傷的貢獻大于波浪載荷。

③相對于風浪同向，風浪異向對熱點疲勞損傷影響較大，并且風浪方向錯位角度越大疲勞損傷越大。

④風和波浪產生的疲勞損傷相加會嚴重低估導管架和塔筒底部的疲勞損傷，而應力相加的方法則會預報出偏保守的結果，本文結果可用于支撐結構初步的疲勞損傷設計。