基于拓撲優化的機床立柱設計

孫文輝，李天箭

（200082 上海市 上海理工大學 機械工程學院）

0 引言

隨著現代制造業的高速發展,機床各個部件都在往高精度與高性能方向發展[1]，不僅要求機床部件的精度要高，還要求其性能更好[2]。機床在工作時，立柱對整個機床的模態、剛度都起到很重要的作用，還能起到支撐整個機床結構的作用，因此立柱的剛度以及固有頻率大小對機床來說很重要。

機床的性能固然重要，而對于機床部件的設計，大多數設計者還都只停留在經驗設計與結構類比的階段[3-4]，這可能不會使設計部件的性能提高更多，拓撲優化技術可以目標性地提高結構的性能，能給零件的結構設計提供有效的參考，在機床的零部件結構的設計中已經得到廣泛應用[5]。拓撲優化技術可以使構型內部的力流更加有效地傳遞，還可以減少材料屬性，縮減成本，所以從輕量化與經濟效益方面著手[6]，拓撲優化技術有一定的優勢。

在本文中利用拓撲優化技術，通過有限元軟件ANSYS Workbench 對立柱進行拓撲優化。在考慮到機床工作時，立柱與主軸箱的連接部位會有多種工況產生，這時要分3 種不同情況分析，從而在以提升一階固有頻率為目標的前提下，得出理想的立柱構型。

1 立柱有限元模型建模

機床由很多部件組成，其中包括床身、立柱、主軸箱、主軸、工作臺等幾大部分。本文主要研究機床立柱的性能。一般機床的內部都是空心的，在本文中建立的有限元模型是實體的結構，對建立的實體的模型進行拓撲優化，得出一定的構型，對新的模型重新計算與重構，從而設計出滿足一定要求的立柱模型。立柱的有限元模型實體結構如圖1 所示。此模型為長360 mm，寬460 mm，高120 mm，且主軸箱位于上工況位置時的一種情況，連接部位簡化為上工況受力面。

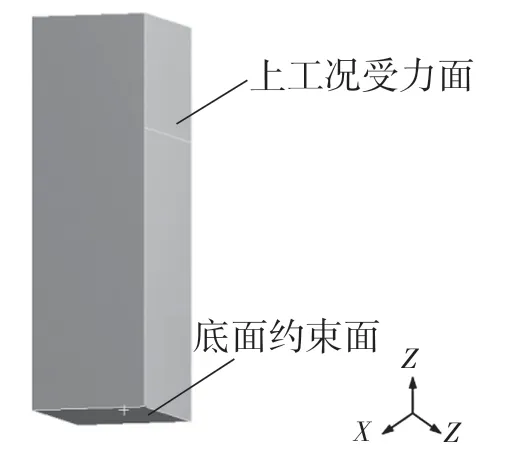
圖1 立柱實體結構Fig.1 Column structure

建立有限元模型后，將立柱實體結構模型導入ANSYS Workbench 中，將材料設置為鑄鐵。鑄鐵的密度為ρ=7.2×103kg/m3，泊松比為μ=0.28，彈性模量為E=110 GPa。將立柱模型劃分單元網格，單元數25 254 個，節點數109 966 個。進行模態分析，模態分析時將底面約束面固定住，經過分析可以得出此模型的前6 階固有頻率。各階固有頻率如表1 所示。

表1 立柱前6 階模態的固有頻率Tab.1 Natural frequencies of the first six modes of column

其中1 階振型如圖2 所示。

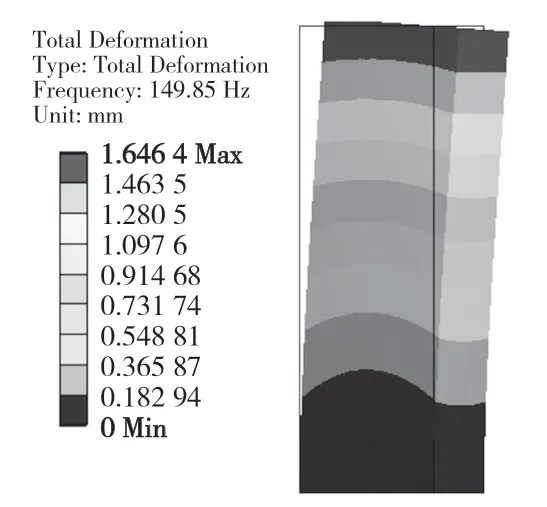
圖2 1 階振型Fig.2 First mode

2 拓撲優化

2.1 拓撲優化數學模型建立

拓撲優化的方法有很多種，本文采用的是變密度法對模型進行拓撲優化，以最大剛度為目標，提升一階固有頻率。

材料宏觀物理量與材料的密度之間存在非線性關系

式中：Ei——單元i 彈性模量；μ0——材料的初始泊松比；μ——泊松比；p——密度懲罰因子，常取p=3；ρi——單元相對密度。

變密度法的數學模型如式（2）-式（3）：

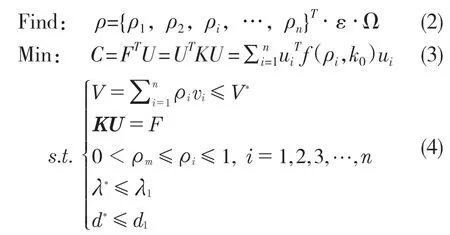
式中：ρ——單元密度單位向量；n——結構里面單元的數量；K——結構總剛度矩陣；F——節點處載荷；U——位移產生的向量；C——結構柔度值；ui——單元i 節點位移向量；k0——剛度矩陣常量；ρm——相對密度最小的變量；λ1——1 階固有頻率；λ*——原始1 階固有頻率；d1——最大變形位移；d*——原始最大的變形。

2.3 三種工況下拓撲優化

機床工作時，立柱部分既要考慮底部與底座相接觸部分，也要考慮側面與主軸箱接觸部分。底面部分可以采用固定端約束，而側面則需考慮其受力情況。而在機床工作時往往會遇到多種加工工況，這樣就要考慮機床在多種工況下拓撲優化的情形，這里采用立柱部分與主軸箱部分連接在一起的情況來進行研究。由于機床運轉的多樣性，采用主軸箱位置在上工況位置、中工況位置與下工況位置3 種情況分別進行拓撲[7]，探究立柱的拓撲結構變化與規律。3 種工況如圖3 所示。

圖3 上、中、下三種工況Fig.3 Upper,middle and lower working conditions

對3 個模型分別添加載荷與約束，如圖4 所示。C，D 四個面受力大小方向一致。A 為向下的重力作用，B 為主軸下端面模擬加工受的三項力，C 為多工況運行軌道受三項力，D 面為固定約束面。

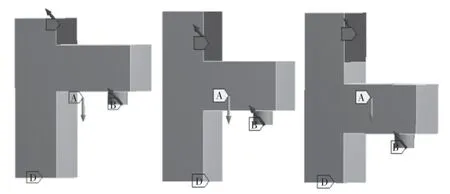
圖4 模型受力Fig.4 Model stress

分別進行35，35，31 次迭代之后得出其拓撲結果，如圖5 所示。

圖5 三種工況拓撲結果Fig.5 Topological results of three working conditions

2.4 立柱計算外力與單獨拓撲

上述情況為多工況情況，是由立柱加主軸箱兩部分結合在一起進行分析，現就立柱部分在拆開之后，需要考慮力通過主軸箱傳遞給立柱[7]，力的大小在立柱右側面的分布情況進行研究，在其他面受力不變情況下，探討主軸箱與立柱接觸部分的力傳導情況。以上工況為例，即主軸箱與立柱接觸面在立柱右側的最上端，其受力情況如圖6 所示。

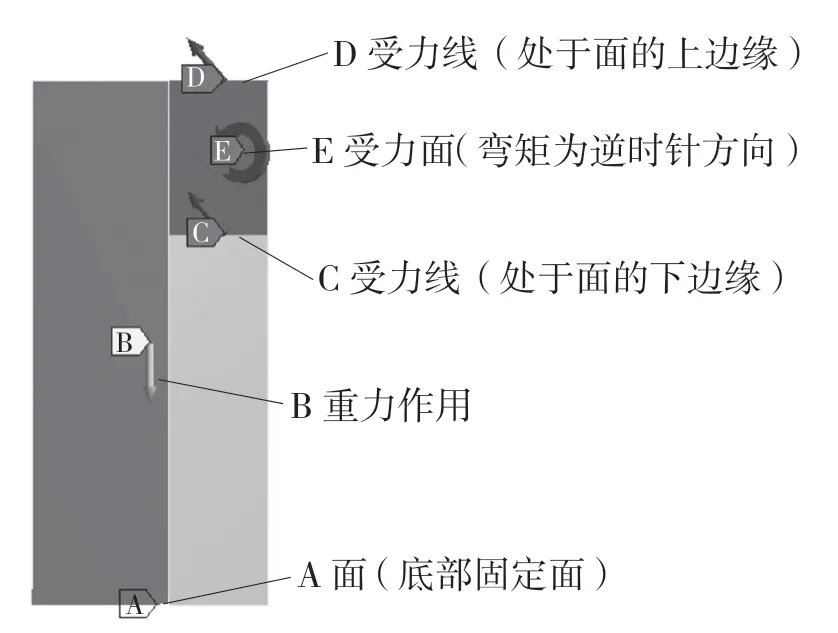
圖6 立柱受力情況Fig.6 Stress condition of column

圖6 中E 受力面為上工況時主軸箱與立柱的接觸面，機床工作時，主軸箱上的力對此面產生彎矩作用，此彎矩如圖6 所示，E 受力面添加一個逆時針的彎矩作用。而這個面的受力大小分布可能會不均勻，現對其D 受力線與C 受力線即上下兩部分進行探討，研究兩個部分的力大小分布權重關系。

現對D 受力線與C 受力線的權重做比較。原先合力的大小為定值，現改變兩者大小比例值，如表2 所示。其中XD/YD 與XC/YC 分別為D 受力線與C 受力線在X 和Y 方向受力大小。

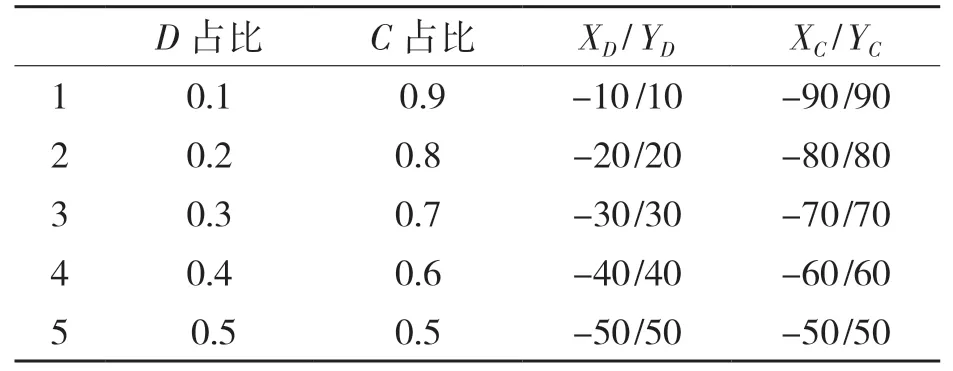
表2 計算外力Tab.2 Calculation of external force

表2 數據中，力的單位為kN。XD/YD與XC/YC力大小的總和為100 kN，現討論兩個部位的力占比情況與拓撲結果做對比，其各個受力大小不同情況拓撲出結果如圖7 所示。

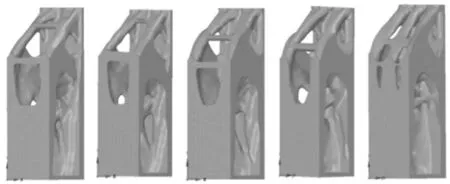
圖7 立柱拓撲結果Fig.7 Column topology results

對這5 種拓撲結果分別進行后處理與重新計算其變形情況，其5 種情況最大整體變形如表3所示。

表3 不同情況變形大小Tab.3 Deformation size under different conditions

由其結果可以看出，比例為0.2/0.8 時的變形為0.287 mm，其整體變形量比其他4 種結果變形較小，則此受力比例較其他4 種較優。此拓撲模型的下面線受力更大，上面線的受力較小。經過后處理重新分析此模型，得出應力與整體變形大小，其靜應力與整體變形大小如圖8 所示。

圖8 靜應力與變形Fig.8 Static stress and deformation

由結果可知，其最大等效應力為22.64 MPa，整體變形為0.287 18 mm。

對此拓撲模型進行模態分析，可以得出前6階固有頻率，如表4 所示。

表4 前6 階模態的固有頻率Tab.4 Natural frequencies of the first six modes

由表4 可以看出，拓撲模型的一階固有頻率為177.1 Hz。拓撲模型一階振型由圖9 所示。

圖9 拓撲模型1 階振型Fig.9 First mode shape of topological model

3 模型重構

根據立柱拓撲結果初步重構出其模型，如圖10 所示。

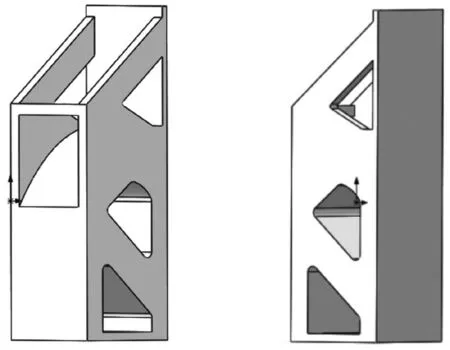
圖10 立柱重構模型Fig.10 Column reconstruction model

對重構出的模型重新進行分析，得到其應力、變形與應變，如圖11 所示。

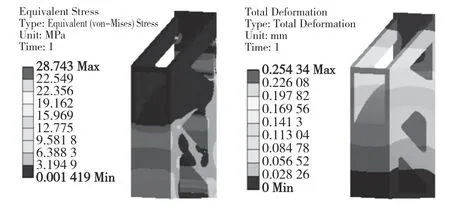
圖11 重構模型的應力與變形Fig.11 Stress and deformation of reconstructed model

由重新分析可以得出最大等效應力大小為28.743 MPa，其位于立柱與底座接觸結合部右側；整體變形最大值為0.254 34 mm；應變與應力成正比，大小為0.000 265 64 mm。可以看出整體變形比拓撲結果小，其剛度性能良好。

將重構的模型底面固定后進行模態分析，分析出重構模型的前6 階固有頻率，如表5 所示。

表5 前6 階模態的固有頻率Tab.5 Natural frequencies of the first six modes

由模態分析得出，前6 階固有頻率，其中1階固有頻率為237.3 Hz。重構模型一階振型如圖12 所示。

圖12 重構模型1 階振型Fig.12 The first mode shape of reconstructed model

4 拓撲模型與重構模型模態對比

原始實體模型為149.8 Hz，拓撲模型為177.1 Hz，而重構模型的一階固有頻率為237.2 Hz，可以看出重構模型與拓撲模型的1 階固有頻率都高于原來的拓撲之前的1 階固有頻率。現將拓撲模型與重構模型的前6 階固有頻率進行對比，如圖13 所示。

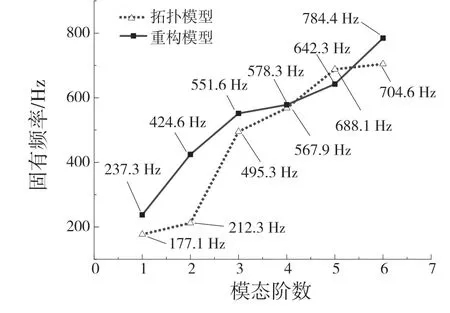
圖13 前6 階模態對比Fig.13 Comparison of the first six modes

重構模型的前6 階固有頻率總體上要略高于拓撲模型的前6 階固有頻率。在機床運轉時，最主要看1 階固有頻率的大小，1 階固有頻率越大，那么它在工作時的性能就越好。拓撲模型與重構模型1 階固有頻率都大于原始實體模型的1 階固有頻率，總體上性能得以提升。

5 結論

利用拓撲優化方法探究了立柱結構型與性能，對一個立柱的實體結構進行拓撲，拓撲過程中考慮到多種加工工況，對上中下3 種工況進行拓撲優化，分別得到其構型。對立柱單獨優化考慮了力通過主軸箱部分傳遞給立柱的分布情況，分為5 種情況，最終以變形大小選擇較優模型。通過此法得到的模型與多種加工工況得到的模型類比，重構一個模型。將他們的性能對比，發現重構模型與拓撲模型的1階固有頻率都有所提升，重構模型的前6 階固有頻率更好，而且重構模型的總體變形也比拓撲模型的低，則此模型較優。