矩陣變換器-永磁同步電機系統旋轉矢量共模電壓抑制策略

鄧惟滔，鐘琪，劉郁，奚菲若，陳俊杰

(湖南理工學院 信息科學與工程學院，湖南 岳陽 414006)

0 引 言

近年來，在新的科技革命和全球經濟趨于一體化的背景下，我國的建設步伐不斷加快，裝備制造業面臨的技術需求日益提高，給電機系統的發展注入新的動力，同時也對電機系統及其控制技術提出了更高要求[1-5]。矩陣變換器(matrix converter,MC)-永磁同步電機(permanent magnet synchronous motor, PMSM)直接轉矩控制(direct torque control, DTC)技術在功率密度、運行效率、動態性能等方面的優勢在推動高端裝備制造的國產化、自主化過程中具有重要地位，研究開發高控制精度、高功率密度以及高運行效率的永磁同步電機系統是推進裝備高端化發展的關鍵。文獻[6-7]將矩陣變換器與直接轉矩控制技術相結合，應用于永磁同步電機系統，在解決矢量控制存在的參數變化大以及動態響應時間長等問題基礎上，同時實現了永磁同步電機系統的調速控制。

由于傳統永磁同步電機的直接轉矩控制技術存在磁鏈和轉矩脈動大、轉矩脈動造成的高頻噪聲等問題，基于自抗擾技術的滑模控制[8]、矢量雙選取控制[9]、基于空間矢量調制的無磁鏈環直接轉矩控制[10]、改進的模型預測控制[11]、雙滑模控制[12]以及優化占空比的直接轉矩控制[13]等控制策略明顯地減小了轉矩脈動并保持了傳統直接轉矩控制優良的動靜態性能。針對傳統矩陣變換器的永磁同步電機直接轉矩控制存在輸入電流質量差、轉矩磁鏈波動過大和開關頻率不固定的缺陷，主從矢量的占空比控制、占空比優化、最優矢量、動態轉矩滯環比較器以及采用不同幅值矢量的直接轉矩控制策略分別被提出，實現了電機系統轉矩、磁鏈的平滑控制，改善了輸入電流質量，達到良好的動、穩態調速性能[14-19]。

上述控制策略均能實現直接轉矩控制優良的動靜態性能，但是都存在共模電壓大的問題，從而縮短電機壽命。文獻[20- 21]分析基于雙空間矢量調制的MC-PMSM系統電機共模電壓產生機理，提出合理選擇零矢量，將60°相區內的1個零矢量用2個不同狀態的零矢量替換的方法，從而降低電機共模電壓峰值。文獻[22]將混合調制算法應用在定子磁鏈控制系統中，實現在全功率因數條件下寬調制范圍內對基于三相四開關逆變器的PMSM驅動系統共模電壓的有效抑制。文獻[23]和文獻[24]分別提出了一種新的有限控制集模型預測控制和新的直接轉矩控制解決方案，只選擇六個不產生共模電壓的旋轉矢量來驅動電機運行，以消除矩陣變換器-永磁同步電機系統中的共模電壓。但該方法在降低共模電壓的同時不能保證良好的穩態性能，明顯增大了轉矩波動和電流諧波含量。

本文針對矩陣變換器永磁同步電機的傳統直接轉矩控制策略存在共模電壓較大的問題，提出采用旋轉矢量替換有效矢量來抑制共模電壓的方案，通過統計分析旋轉矢量、有效矢量相角隨輸入電壓相角的變化規律，建立新的開關表并進行實驗驗證。

1 傳統矩陣變換器直接轉矩控制

圖1為矩陣變換器-永磁同步電機系統結構簡圖。3×3型矩陣變換器使用9個雙向開關來實現從輸出相到任意輸入相的連接。

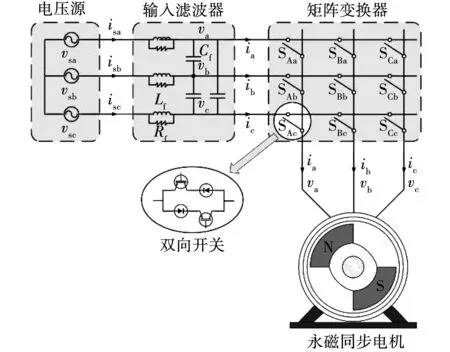
圖1 矩陣變換器-永磁同步電機系統結構簡圖Fig.1 Matrix converter-permanent magnet synchronous motor system structure diagram

矩陣變換器的輸入側不允許短路、輸出側不允許開路，符合該約束條件的27種開關狀態對應的輸出電壓矢量幅值和相角如表1所示。表中Vim與α分別表示輸入電壓矢量的幅值和相角。

開關狀態±1～±9對應有效矢量，分別在各自方向上做脈振運動，脈振幅度隨相應線電壓瞬時值變化。根據表1可知，在任意時刻矢量平面內相角為0°、60°、120°、180°、240°、300°這6個方向上都會存在電壓有效矢量，這6個方向依次記為V1～V6。不難發現這6個方向與兩電平逆變器6個有效矢量的方向一致，因此傳統MC-DTC可分兩步來選取電壓矢量：第一步，根據表2所示兩電平逆變器開關表從V1～V6中選取一個矢量方向；第二步，根據表3從矩陣變換器的有效矢量中選擇一個位于該方向的矢量。

表1 輸出電壓矢量幅值和相角Table 1 Output voltage vector magnitude and phase angle

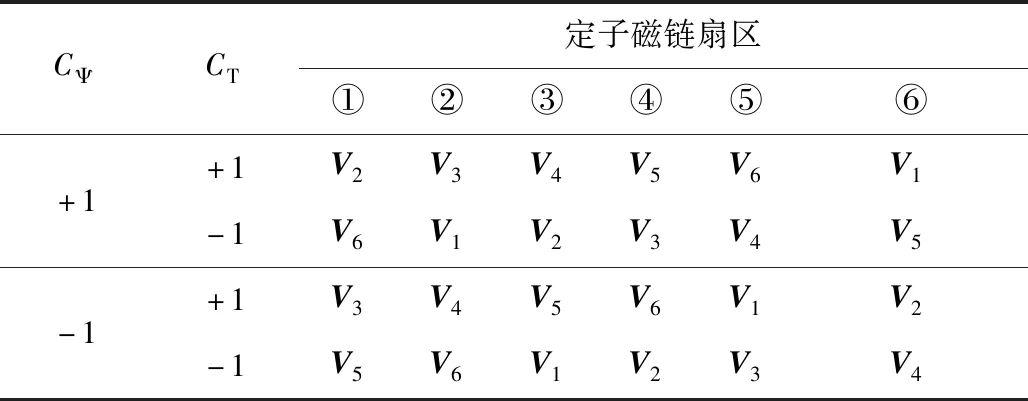
表2 兩電平逆變器開關表Table 2 Two-level inverter switching table

表3 矩陣變換器開關表Table 3 Matrix converter switch table

2 新型矩陣變換器直接轉矩控制

傳統矩陣變換器-永磁同步電機系統直接轉矩控制策略使用有效矢量，存在共模電壓過大的問題。由于旋轉矢量的共模電壓為0，本文用旋轉矢量替換與其方向相同或相近的有效矢量，達到減小共模電壓的目的。

2.1 旋轉矢量同向替換

旋轉矢量的方向隨輸入電壓相角α不斷變化，如果在某一時刻，旋轉矢量和某個有效矢量的相角相同，就可用旋轉矢量替換該有效矢量。圖2所示為α=60°時旋轉矢量同向替換過程分析圖。

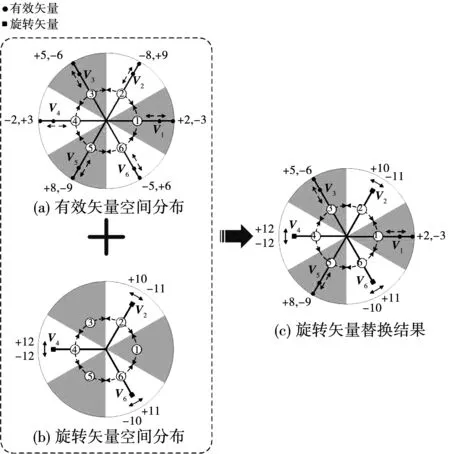
圖2 α=60°旋轉矢量同向替換過程Fig.2 Vector replacement of α=60°

圖2中，“●”表示有效矢量，“█”表示旋轉矢量，箭頭表示旋轉矢量的空間轉動方向或有效矢量的幅值脈振方向。

當α=60°時，根據表3可得位于V1、V2、V3、V4、V5、V6方向上的輸出電壓有效矢量依次為+2/-3、-8/+9、+5/-6、-2/+3、+8/-9、-5/+6，如圖2(a)所示。根據表1可知α=60°時旋轉矢量-11/+10、±12、+11/-10的相角分別為60°、180°、300°，即分別處于V2、V4、V6方向，如圖2(b)所示。因此，此時V2、V4、V6方向上的有效矢量可以用同方向的旋轉矢量-11/+10、±12、+11/-10分別替換，如圖2(c)所示。

同理，采用上述方法將輸入電壓相角α=0°、120°、180°、240°、300°時的有效矢量替換為相應旋轉矢量，分別如圖3(a)～圖3(e)所示。

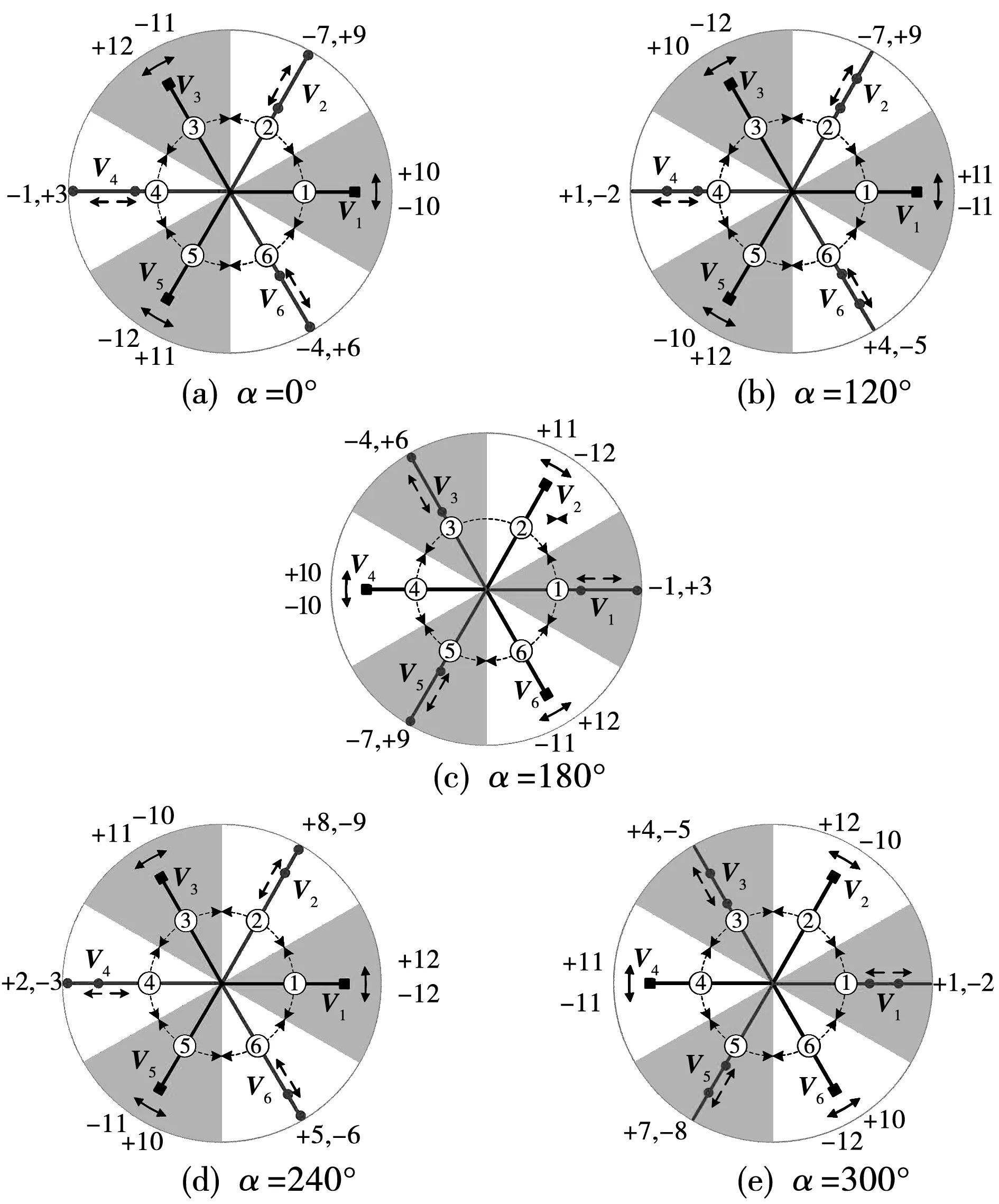
圖3 旋轉矢量同向替換結果圖Fig.3 Vector replacement

2.2 旋轉矢量范圍替換

根據2.1節，在輸入電壓相角為特定值的幾個離散時刻用旋轉矢量替換跟它同向的有效矢量，無法在整體上對系統性能產生影響。因此，須在輸入電壓相角的一定區間范圍內實施矢量替換。本文提出的替換方案為：當旋轉矢量與有效矢量的夾角|β-γ|(β為有效矢量相角，γ為旋轉矢量相角)在一定誤差范圍θ之內，即|β-γ|≤θ時, 可用旋轉矢量替換該有效矢量(誤差范圍θ應不對電機的控制效果產生顯著影響)。如圖4(a)所示，在V1～V6順、逆時針θ夾角扇區范圍(圖中用綠色陰影部分表示)內的旋轉矢量，均可替換該方向的有效矢量。替換范圍可表示為(Xπ/3-θ,Xπ/3+θ),X=0,1,2,3,4,5。

當輸入電壓相角α∈(-θ,θ)時，如圖4(b)所示，圖中紅色陰影部分表示旋轉矢量可能位于的位置范圍。比較圖4(a)和圖4(b)可知，此時間段+10/-10旋轉矢量的位置范圍為(-θ,θ)，與V1方向的矢量替換范圍相同，故可以替換該區間范圍內的有效矢量+1/-3。同理，旋轉矢量+12/-11可以替換V3方向上的有效矢量+4/-6，旋轉矢量-12/+11可替換V5方向上的+7/-9。替換后的矢量如圖4(c)所示。

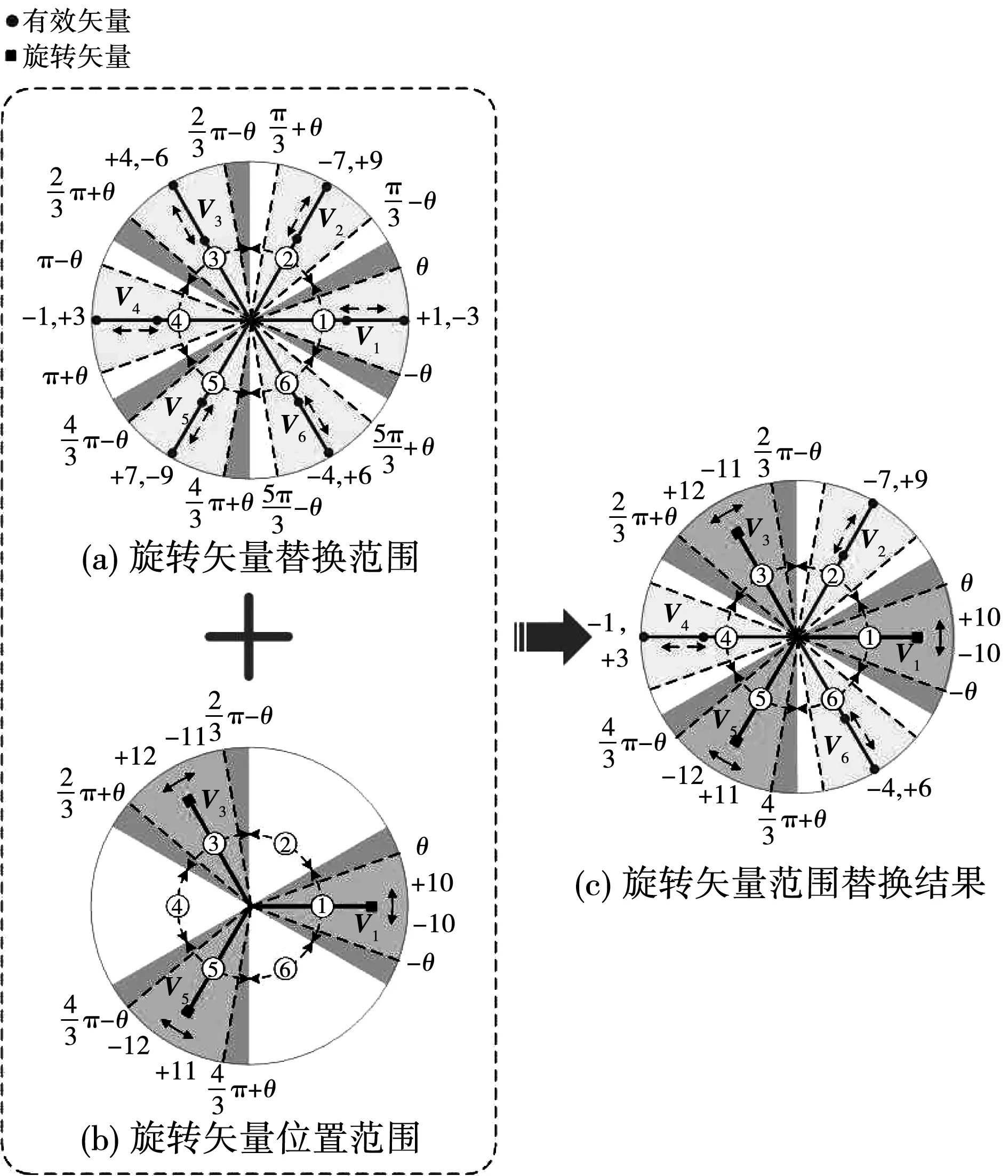
圖4 α∈(-θ,θ)旋轉矢量范圍替換過程Fig.4 Vector replacement of α∈(-θ,θ)

同理可得輸入電壓相角α位于其他5個扇區時旋轉矢量范圍替換情況，如圖5所示。

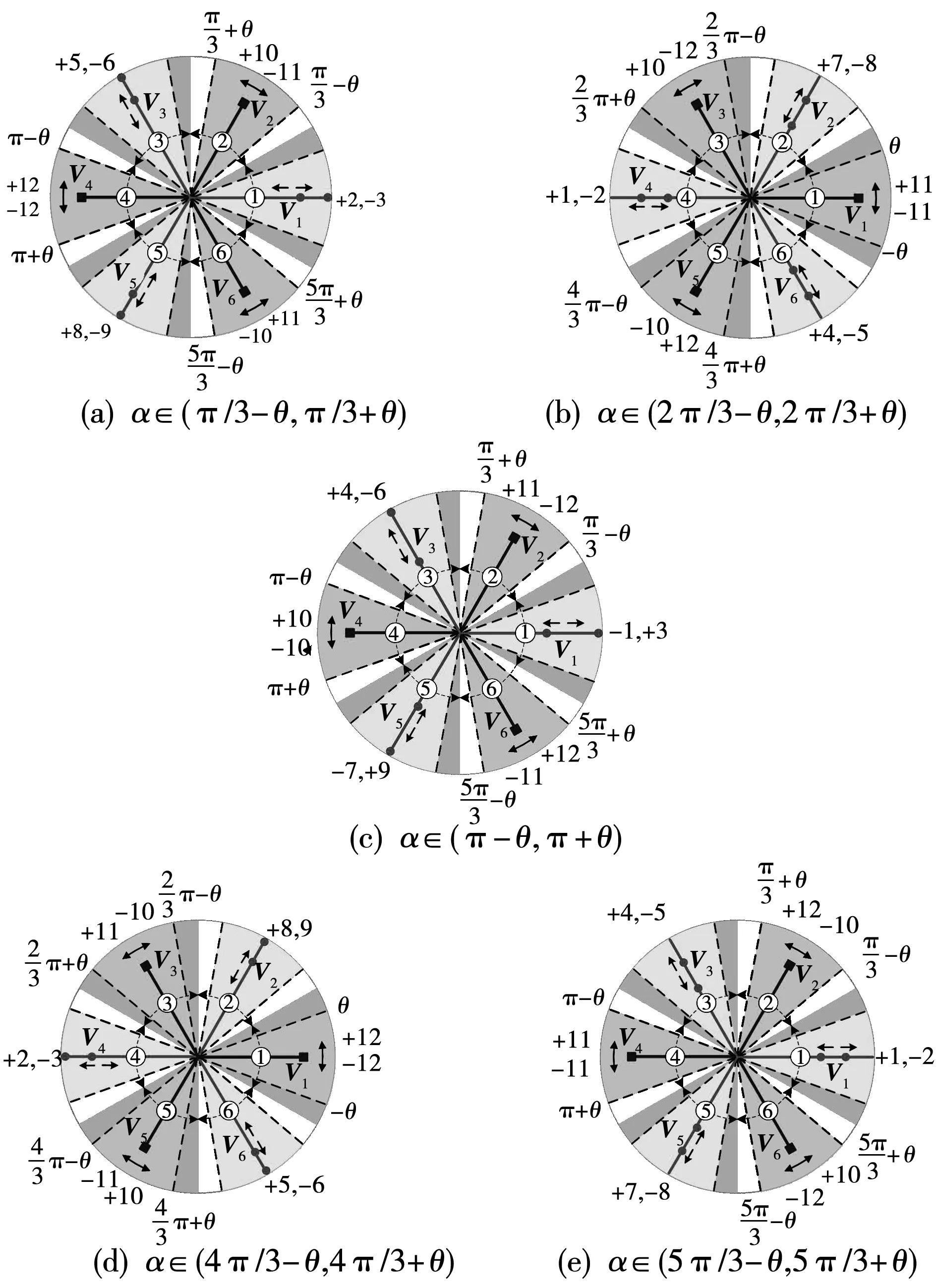
圖5 旋轉矢量范圍替換結果圖Fig.5 Diagram of vector replacement

2.3 新型開關表建立

根據2.2節將傳統MC-DTC開關表(表3)中的部分有效矢量替換為旋轉矢量，即得到新型矩陣變換器開關表，如表4所示。表中每格符號“/”左側矢量記為l矢量，“/”右側矢量記為r矢量。當查表所得為有效矢量時，采樣傳統MC-DTC篩選方案。當查詢表4所得矢量為旋轉矢量時，以開關切換次數最小為原則從l矢量和r矢量中進行最終篩選。根據圖1，構建第k個采樣周期的傳輸矩陣為

(1)

式中：Sho(k)為雙向開關Sho的開關函數，Sho(k)=1表示開關閉合，Sho(k)=0表示開關斷開，h∈{A,B,C}，o∈{a,b,c}；M為矩陣變換器的傳輸矩陣。開關狀態變化數量的計算可表示為

F=f[M(k+1)-M(k)]；

(2)

(3)

式中mij表示傳輸矩陣M中第i行第j列的元素。

將l矢量和r矢量分別代入上式并比較得

(4)

根據比較結果進行最終篩選。整個控制過程的流程圖如圖6所示。首先，根據轉矩、磁鏈滯環比較器輸出和定子磁鏈所在扇區查詢兩電平逆變器開關表(表2)，選擇一個確定的矢量方向；然后，再根據確定的矢量方向和輸入電壓相角α查詢新型矩陣變換器開關表(表4)，得到兩個矢量；如果所得矢量為旋轉矢量，則根據開關轉換次數觀測結果最終選定一個旋轉矢量；如果所得矢量為有效矢量，則根據傳統MC-DTC的滯環比較器輸出最終選定一個有效矢量。

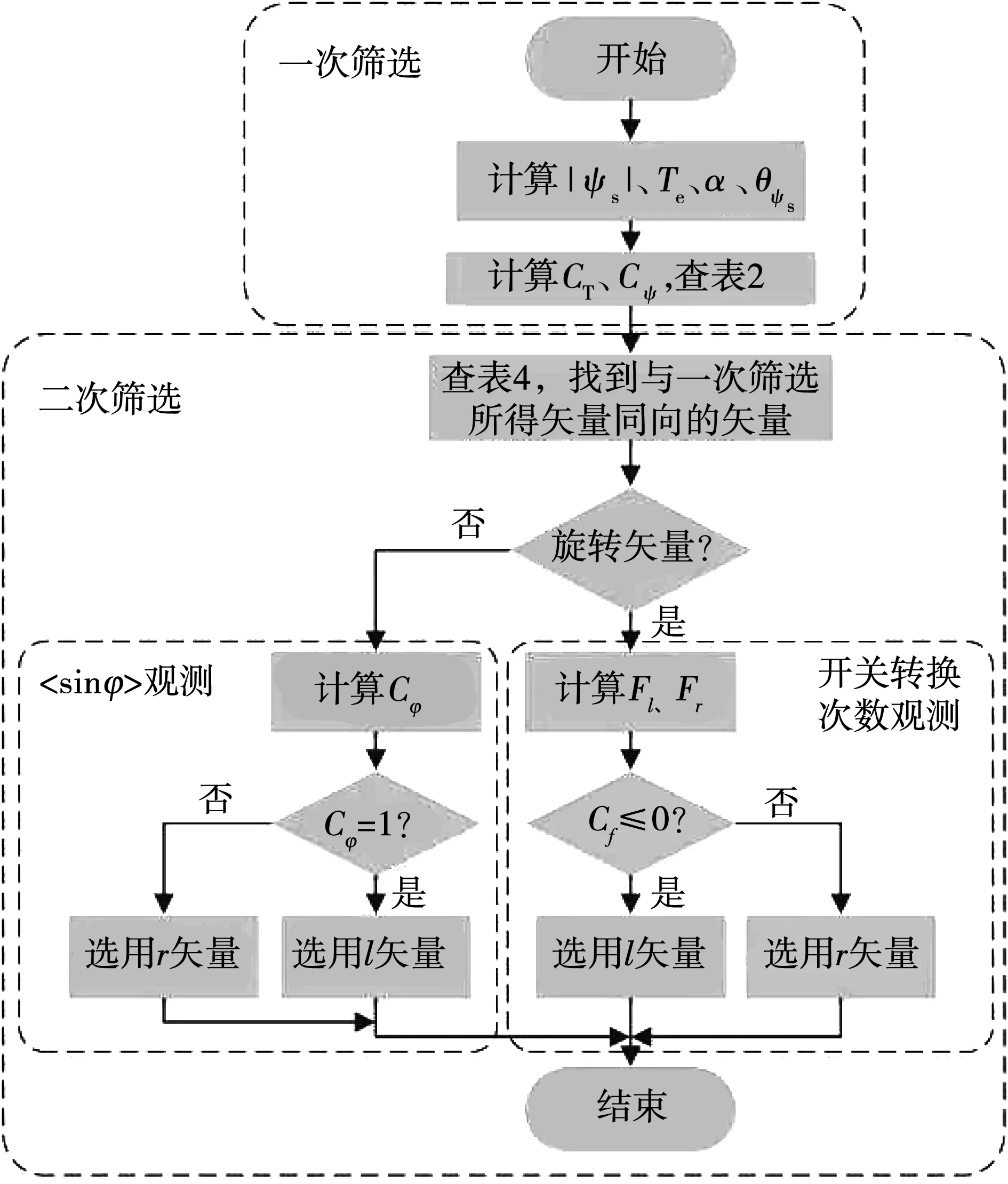
圖6 旋轉矢量控制策略控制流程圖Fig.6 Flow chart of rotation vector control strategy

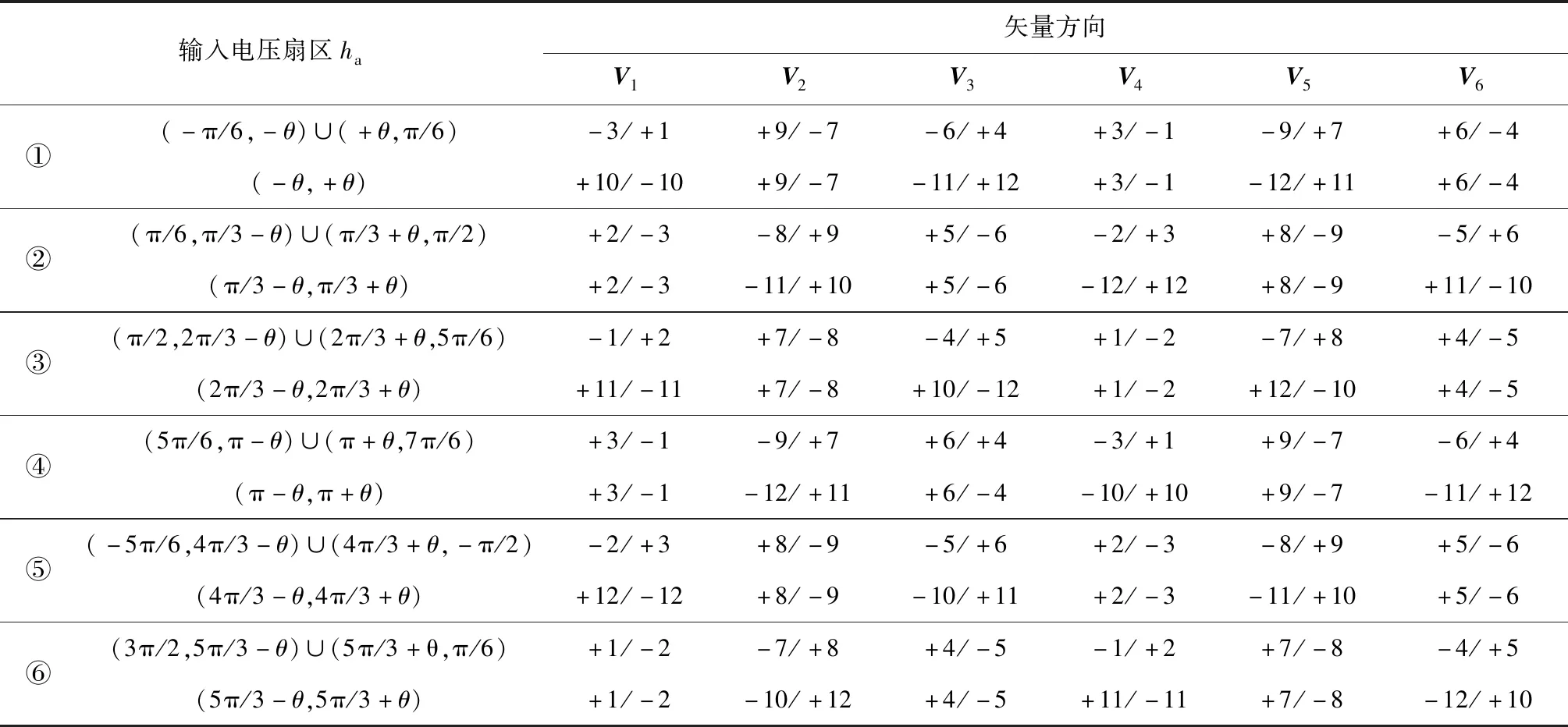
表4 新型矩陣變換器開關表Table 4 New matrix converter switching table

新型MC-DTC控制策略結構圖如圖7所示。圖中，Cφ表示傳統MC-DTC的滯環比較器的輸出，其中：符號<>表示平均值；φ為輸入相電壓矢量超前于輸入電流矢量的角度。

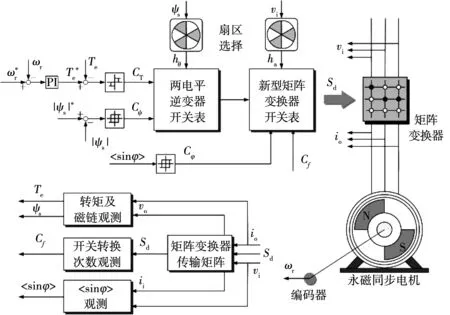
圖7 新型MC-DTC控制策略結構簡圖Fig.7 Diagram of the proposed MC-DTC

3 實驗驗證

采用一臺1.6 kW永磁同步電機對傳統MC-DTC和新型MC-DTC策略進行實驗研究。

實驗系統樣機如圖8所示。被控電機與負載電機為相同型號的永磁同步電機，額定轉速為1 000 r/min，額定轉矩為15 N·m，負載電機作發電機運行，其轉子與被控電機連軸，定子連接三相對稱電阻負載。

圖8 MC-PMSM系統樣機Fig.8 Experimental setup

控制器由DSP芯片TMS320F28335和FPGA芯片EP4CE6構成。其中，電壓、電流采樣及DTC程序在DSP中實現；換流控制采用四步換流法，在FPGA中完成。傳統MC-DTC與新型MC-DTC控制周期均為100 μs，新型MC-DTC中θ取值為π/6。

實驗中電機轉速先從400 r/min階躍至-400 r/min，1 s后再階躍回400 r/min。圖9分別給出了傳統算法和新型算法的電機轉矩、轉速和定子A相電流的動態過程波形。可以看出，新型算法和傳統算法均具有良好的動態性能。

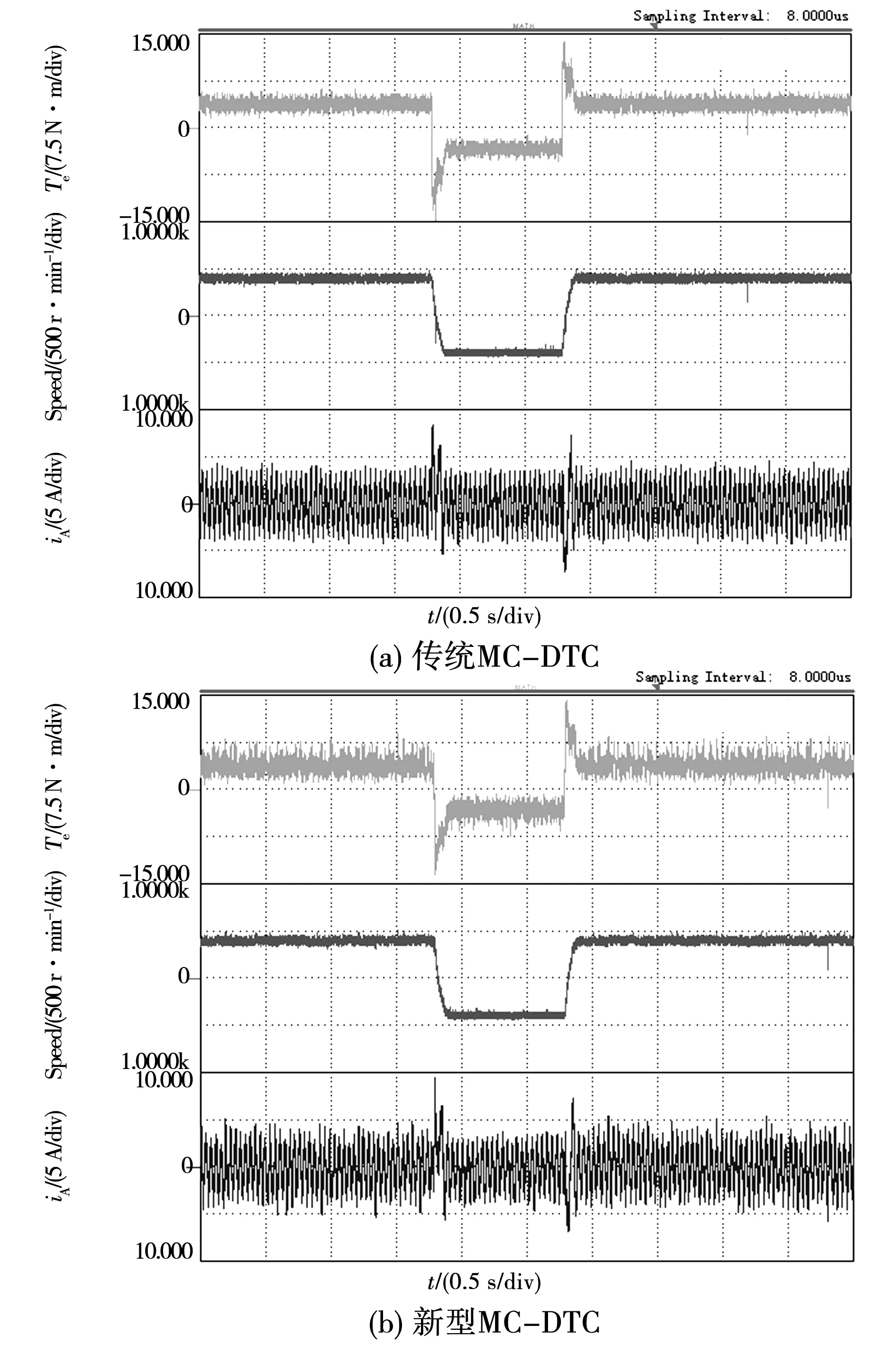
圖9 動態實驗波形Fig.9 Dynamic performance

圖10為400 r/min時兩種算法下的穩態波形。

其中圖10(a)為傳統算法的共模電壓、電磁轉矩、定子電流、MC輸入電流的穩態波形，圖10(b)為新型算法的相應波形。對比共模電壓的波形可見，傳統算法的共模電壓均方根(root mean square，RMS)值為20.2 V，而新型算法由于采用旋轉矢量，部分時候共模電壓瞬時值為0，RMS值為14.3 V。圖11所示為不同負載條件下共模電壓的RMS值，由圖中可見，與傳統算法相比，新型算法的共模電壓得到有效抑制。

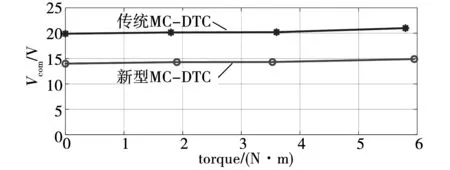
圖11 不同負載條件下的共模電壓Fig.11 CMV at different load condition

對比傳統算法與新型算法的轉矩波形與電流波形可知，新型算法能夠滿足對PMSM控制的基本要求。新型算法的轉矩波動略大，這是由于在輸入電壓矢量相角的某些范圍內，被旋轉的旋轉矢量的位置存在較大偏差，從而降低了對轉矩的控制性能。

4 結 論

本文提出一種共模電壓抑制策略，利用旋轉矢量共模電壓為0的特性，將傳統矩陣變換器直接轉矩控制開關表中部分有效矢量替換為與其方向相同或相近的旋轉矢量。對新型MC-DTC和傳統MC-DTC進行對比實驗研究，結果表明，新型MC-DTC能夠有效降低共模電壓的RMS值，并且能夠滿足系統對穩態性能和動態性能的基本要求。