開槽型盤式異步磁力耦合器調(diào)速特性

楊超君，朱莉，吳盈志，彭志卓，邰蔣西，張磊

(江蘇大學(xué) 機(jī)械工程學(xué)院，江蘇 鎮(zhèn)江 212013)

0 引 言

異步磁力耦合器可通過氣隙的調(diào)控來控制輸出轉(zhuǎn)矩及轉(zhuǎn)速，適用于多種工況，能夠避免傳統(tǒng)傳動(dòng)方式中的摩擦磨損問題，具有節(jié)能性及過載保護(hù)和軟啟動(dòng)等功能，多用于石油、化工等環(huán)境惡劣的領(lǐng)域。異步磁力耦合器在機(jī)械傳動(dòng)中表現(xiàn)出的優(yōu)勢(shì)引起了眾多磁力傳動(dòng)相關(guān)方向?qū)W者的重視[1-7]。

國內(nèi)外許多學(xué)者針對(duì)異步磁力耦合器做了相關(guān)研究，Lubin T等[2]應(yīng)用矢量磁位法推導(dǎo)出盤式異步磁力耦合器的軸向力和轉(zhuǎn)矩的解析表達(dá)式，并分析了磁場(chǎng)分布；Mohammadi等[3]應(yīng)用等效磁路法推導(dǎo)出盤式磁力耦合器磁通密度及轉(zhuǎn)矩的表達(dá)式；Vahid Aberoomand等[4]應(yīng)用等效磁路法推導(dǎo)出雙面永磁軸向渦流耦合器的轉(zhuǎn)矩公式；東華大學(xué)朱姿娜等[5]建立了具有多對(duì)弧形永磁體結(jié)構(gòu)的磁力耦合器的轉(zhuǎn)矩解析模型，對(duì)轉(zhuǎn)矩參數(shù)進(jìn)行了分析；沈陽工業(yè)大學(xué)張炳義等[6]應(yīng)用區(qū)域劃分法對(duì)磁力耦合器的漏磁導(dǎo)進(jìn)行計(jì)算。上述研究致力于耦合器轉(zhuǎn)矩及磁場(chǎng)理論公式的推導(dǎo)，為異步磁力耦合器的性能研究奠定了理論基礎(chǔ)，但未建立異步磁力耦合器的轉(zhuǎn)差率或輸出轉(zhuǎn)速與氣隙之間的關(guān)系(即調(diào)速關(guān)系)，無法通過氣隙厚度的定量調(diào)節(jié)控制從而達(dá)到實(shí)現(xiàn)速度或負(fù)載的調(diào)節(jié)。江蘇大學(xué)楊超君等[7-13]多年來針對(duì)多種結(jié)構(gòu)的磁力耦合器的結(jié)構(gòu)參數(shù)與傳動(dòng)性能、磁場(chǎng)分布以及節(jié)能方面進(jìn)行研究，在此基礎(chǔ)上，近年來也開展了機(jī)械特性、調(diào)速性能的探討，率先提出了調(diào)速關(guān)系模型及調(diào)速特性的研究。其中，文獻(xiàn)[7-10]分別建立了實(shí)心筒式、實(shí)心盤式、鼠籠筒式以及鼠籠(即開槽型)盤式等各類磁力耦合器在恒轉(zhuǎn)矩負(fù)載工況和變轉(zhuǎn)矩負(fù)載工況下的調(diào)速關(guān)系式。但是，上述文獻(xiàn)中對(duì)開槽型盤式異步磁力耦合器(slotted-type axial-flux asynchronous magnetic coupler,SAAMC)調(diào)速特性的研究尚不全面，仍需深入分析探討。

為解決SAAMC的實(shí)際調(diào)速問題，本文以一臺(tái)18極16槽的SAAMC樣機(jī)為例，分析其磁路結(jié)構(gòu)特點(diǎn)，采用等效磁路法推導(dǎo)出其轉(zhuǎn)矩表達(dá)式，并建立恒轉(zhuǎn)矩負(fù)載、二次方率負(fù)載，尤其是恒功率負(fù)載工況下的調(diào)速關(guān)系計(jì)算模型，模擬獲得機(jī)械特性、調(diào)速特性曲線，特別是功率特性曲線，并對(duì)三種負(fù)載下的調(diào)速性能進(jìn)行分析，以及對(duì)其進(jìn)行試驗(yàn)研究，分析工作參數(shù)對(duì)SAAMC調(diào)速性能的影響，驗(yàn)證理論模型的正確性。

1 電磁轉(zhuǎn)矩及調(diào)速關(guān)系模型

1.1 基本結(jié)構(gòu)及調(diào)速機(jī)理

SAAMC的結(jié)構(gòu)模型如圖1所示，導(dǎo)體轉(zhuǎn)子由導(dǎo)體及軛鐵兩部分組成，導(dǎo)體加工有扇形槽，裝配于導(dǎo)體軛鐵的齒上，呈現(xiàn)軛鐵與銅導(dǎo)體的交替排列。永磁轉(zhuǎn)子由軸向均勻充磁的扇形永磁體與軛鐵組成，扇形永磁體沿周向N、S極交替排列，安裝在軛鐵表面。其調(diào)速模型如圖2所示，假設(shè)以永磁轉(zhuǎn)子作為主動(dòng)轉(zhuǎn)子，當(dāng)電機(jī)帶動(dòng)主動(dòng)轉(zhuǎn)子轉(zhuǎn)動(dòng)時(shí)，主動(dòng)轉(zhuǎn)子和從動(dòng)轉(zhuǎn)子之間產(chǎn)生轉(zhuǎn)速差，導(dǎo)體轉(zhuǎn)子切割磁力線產(chǎn)生感應(yīng)電流，感應(yīng)電流產(chǎn)生的感應(yīng)磁場(chǎng)與原永磁磁場(chǎng)耦合實(shí)現(xiàn)扭矩傳遞。磁力耦合器的結(jié)構(gòu)參數(shù)及材料屬性見表1和表2。

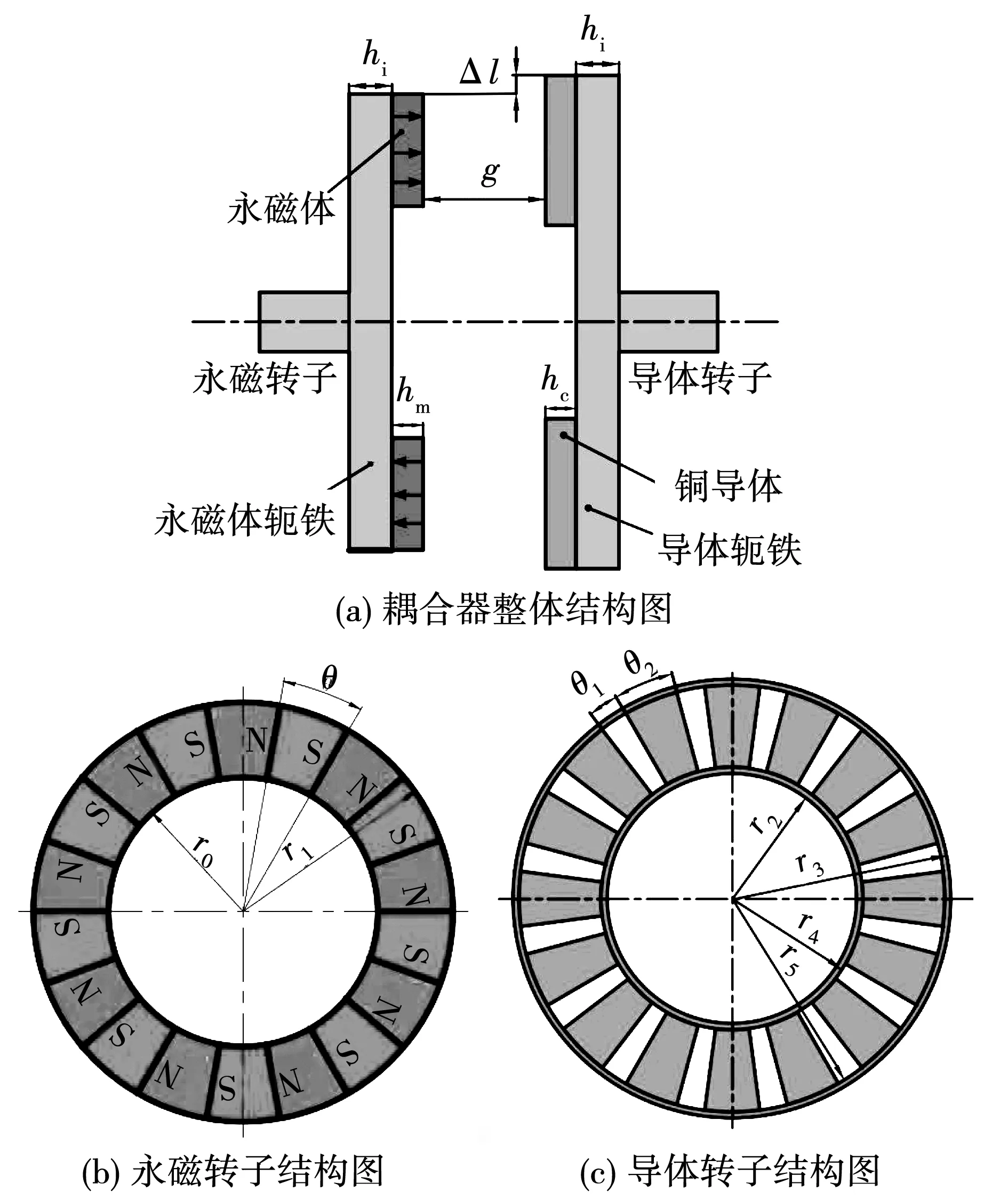
圖1 磁力耦合器結(jié)構(gòu)模型Fig.1 Structural model of the magnetic coupler

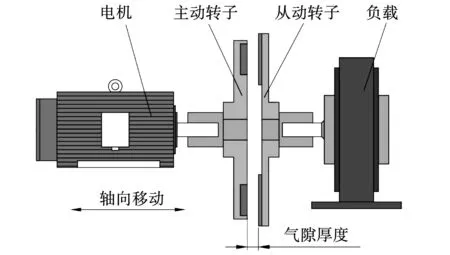
圖2 磁力耦合器調(diào)速模型Fig.2 Speed-control model of the magnetic coupler

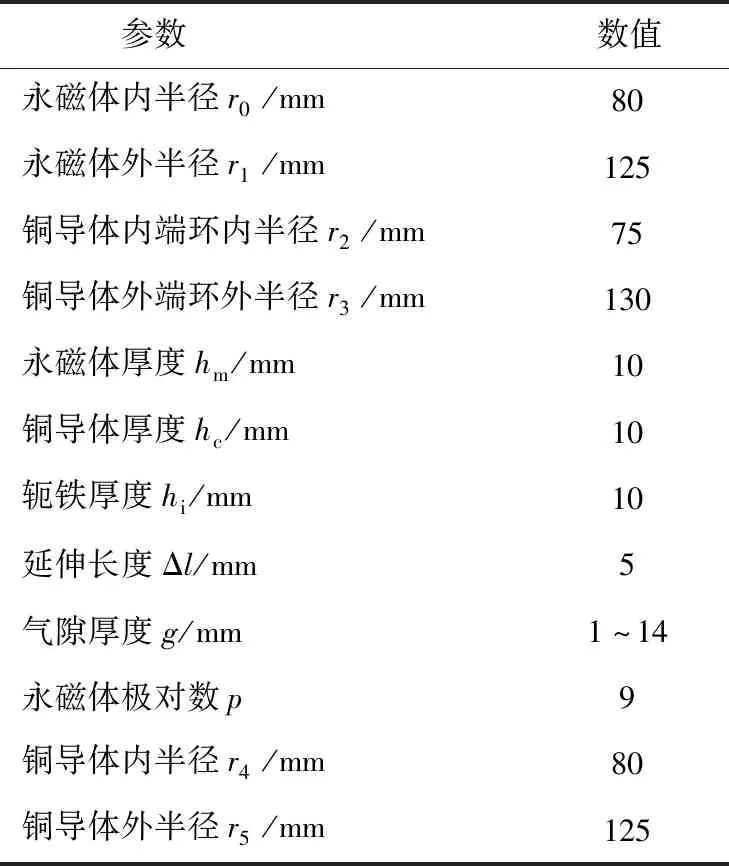
表1 磁力耦合器結(jié)構(gòu)參數(shù)Table 1 Structural parameters of the magnetic coupler

表2 磁力耦合器材料屬性Table 2 Material properties of the magnetic coupler

1.2 電磁轉(zhuǎn)矩計(jì)算公式

為計(jì)算SAAMC的電磁轉(zhuǎn)矩，本文運(yùn)用等效磁路法對(duì)電磁轉(zhuǎn)矩公式進(jìn)行推導(dǎo)。將磁力耦合器在永磁體平均半徑處沿周向展開，從而在此二維展開模型上分析磁力耦合器的磁通路徑。

為便于磁通路徑分析，在進(jìn)行磁場(chǎng)轉(zhuǎn)化為磁路時(shí)，做以下假設(shè)：

1)主磁通量垂直通過永磁體、氣隙和導(dǎo)體盤；

2)僅考慮耦合器永磁體產(chǎn)生的磁場(chǎng)，不考慮感應(yīng)磁場(chǎng)對(duì)原磁場(chǎng)的影響；

3)忽略外界條件對(duì)材料性能的影響，故磁路中各組成部分的材料性能保持不變；

4)磁路中軛鐵不發(fā)生磁飽和，永磁體的磁導(dǎo)率與導(dǎo)體的電導(dǎo)率均為定值。

圖3為磁力耦合器的磁通路徑，主要由3個(gè)部分組成：主磁路Ⅰ、相鄰磁體間漏磁路Ⅱ及單個(gè)永磁體側(cè)面的漏磁路Ⅲ。

根據(jù)圖3所示的磁通路徑，建立SAAMC的等效磁路模型，由于該磁力耦合器的導(dǎo)體盤上存在齒槽，導(dǎo)體與軛鐵交錯(cuò)排布，在耦合器工作的過程中，銅導(dǎo)體層上的磁通路徑經(jīng)過軛鐵和銅兩個(gè)磁導(dǎo)率不同的部分，計(jì)算銅導(dǎo)體層磁阻時(shí)，需要對(duì)軛鐵和銅的磁導(dǎo)率進(jìn)行等效計(jì)算。圖4為磁力耦合器的等效磁路模型，其中，F(xiàn)m為永磁體磁動(dòng)勢(shì)，Φ為總磁通，Φ0為主磁通，Φ1為漏磁通，R0為永磁體磁阻、R1為氣隙磁阻、R2為銅導(dǎo)體磁阻、R3為銅導(dǎo)體軛鐵磁阻、R4為永磁體軛鐵磁阻、R5為相鄰兩磁極間漏磁阻、Rmi為永磁體單側(cè)漏磁阻。考慮到本文所研究的耦合器中永磁體為緊密排布，漏磁路Ⅲ對(duì)整個(gè)磁路的影響甚微，所以永磁體單側(cè)漏磁阻Rmi可以忽略不計(jì)。

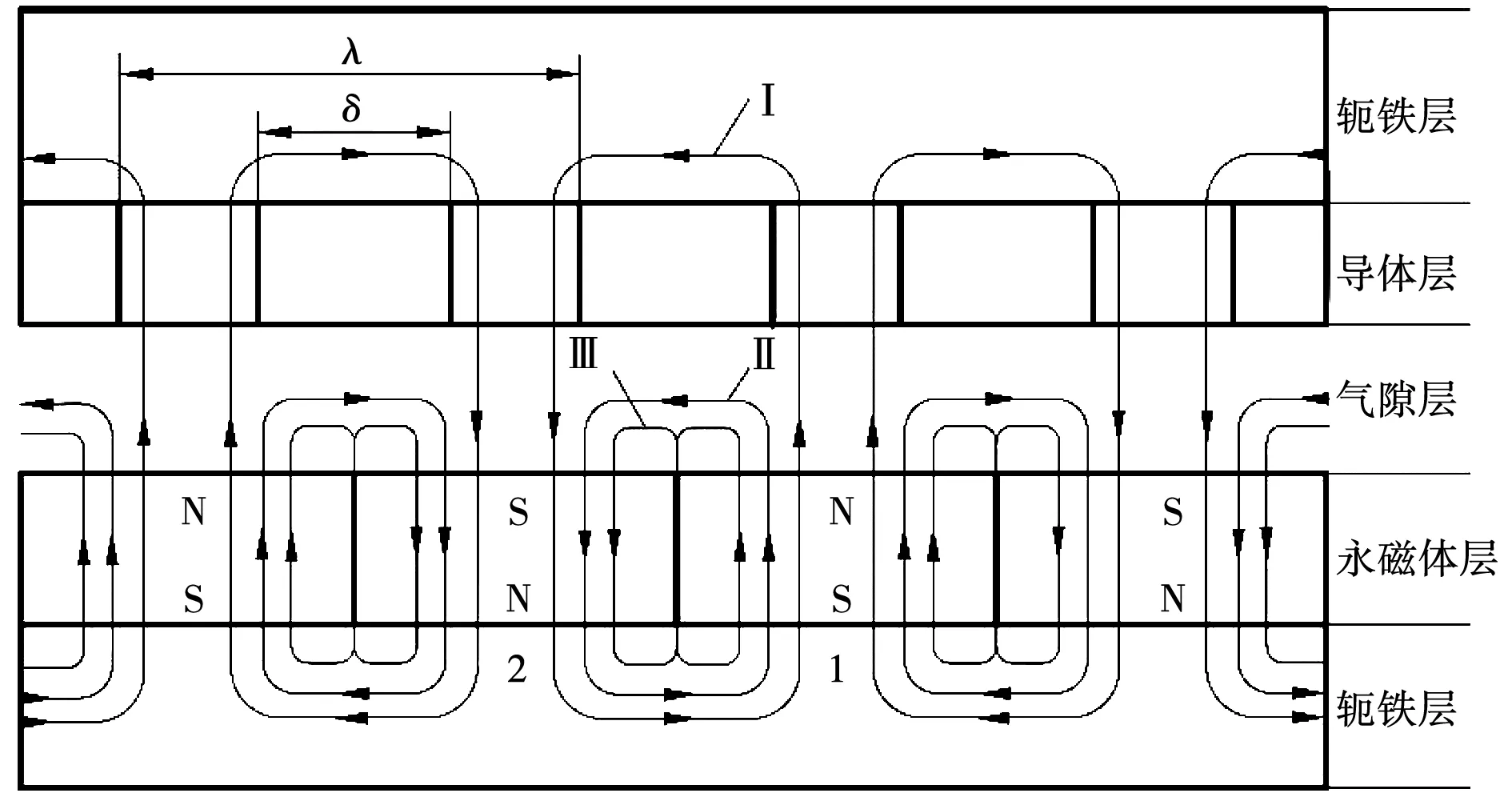
圖3 磁力耦合器磁通路徑Fig.3 Magnetic flux path of the magnetic coupler

圖4中，F(xiàn)m為永磁體的磁動(dòng)勢(shì)源[13]，表達(dá)式為

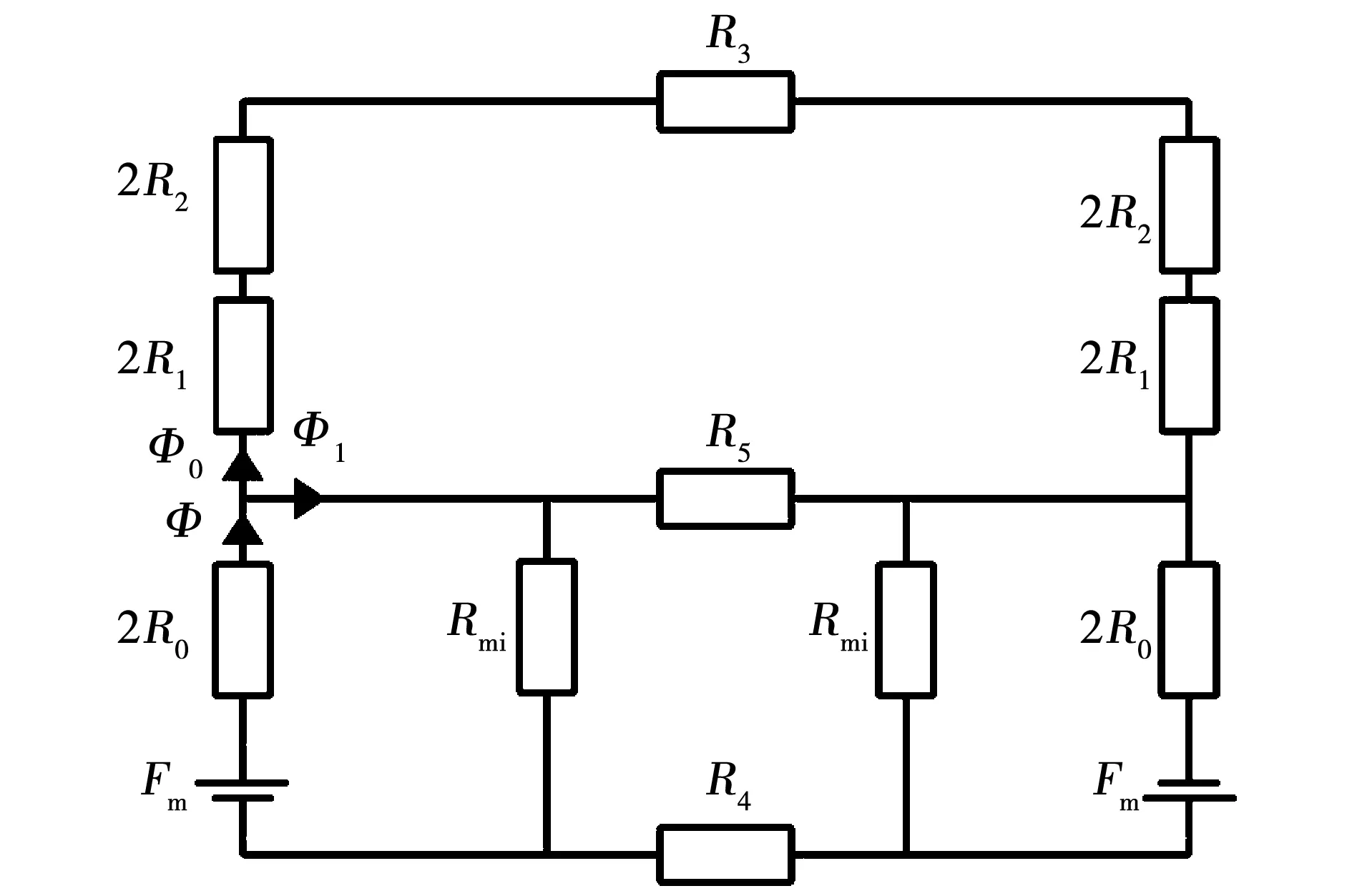
圖4 磁力耦合器等效磁路模型Fig.4 Magnetic equivalent circuit model of the coupler

Fm=Hchm。

(1)

根據(jù)磁阻計(jì)算公式，得到永磁體磁阻、氣隙磁阻、銅導(dǎo)體磁阻、銅導(dǎo)體軛鐵磁阻、永磁體軛鐵磁阻及漏磁阻[14]分別為：

(2)

(3)

(4)

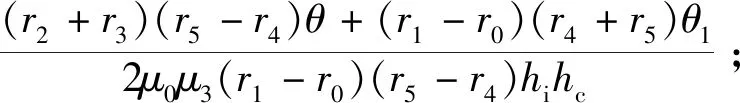
(5)

(6)

(7)

式中：μ0為真空磁導(dǎo)率；μ1為永磁體相對(duì)磁導(dǎo)率；μ2為導(dǎo)體層的等效磁導(dǎo)率；μ3為軛鐵的相對(duì)磁導(dǎo)率；θ為單個(gè)永磁體的圓心角；θ1為齒槽的圓心角；θ2為銅導(dǎo)體的圓心角，如圖1所示。

由于銅導(dǎo)體與軛鐵形成交替排列，導(dǎo)體的磁導(dǎo)率需進(jìn)行等效計(jì)算，其等效磁導(dǎo)率[15]為

(8)

根據(jù)基爾霍夫定律，等效磁路模型中各物理量之間的關(guān)系為：

(9)

將式(2)～式(7)代入到式(9)，可得

Φ0(g)=

(10)

根據(jù)磁通密度的計(jì)算公式，SAAMC關(guān)于氣隙g的平均氣隙磁通密度表達(dá)式為

(11)

為了考慮磁力耦合器實(shí)際運(yùn)行時(shí)，齒槽對(duì)原磁場(chǎng)的影響，引入鼠籠電機(jī)中的卡特系數(shù)[16]，得到磁力耦合器的卡特系數(shù)為

(12)

其中：

(13)

式中：Bg為修正后氣隙磁密；σm為槽寬縮減因子；δ為單個(gè)扇形導(dǎo)體的平均弧長；λ為單個(gè)扇形導(dǎo)體及其相鄰兩個(gè)扇形軛鐵的平均弧長之和，見圖3。

根據(jù)文獻(xiàn)[2]中的電磁轉(zhuǎn)矩計(jì)算方法，結(jié)合式(12)，并考慮三維端部效應(yīng)，得出磁力耦合器的電磁轉(zhuǎn)矩T關(guān)于氣隙厚度g的計(jì)算公式為：

(14)

其中：

(15)

式中：KR為三維校正因子；σ為銅層的電導(dǎo)率；s為轉(zhuǎn)差率；p為永磁體的極對(duì)數(shù)；n0為輸入轉(zhuǎn)速；Kcm為卡特系數(shù)；m、α和γ均為自定義參數(shù)；Δl為導(dǎo)體延伸長度。

1.3 調(diào)速關(guān)系計(jì)算模型

由調(diào)速原理可知，磁力耦合器可以通過調(diào)節(jié)轉(zhuǎn)子間的氣隙厚度g來控制輸出轉(zhuǎn)速nout，并將調(diào)速過程中轉(zhuǎn)子間的氣隙厚度g與輸出轉(zhuǎn)速nout或轉(zhuǎn)差率s間的關(guān)系定義為磁力耦合器的調(diào)速關(guān)系。本節(jié)在1.2節(jié)的基礎(chǔ)上，將建立恒轉(zhuǎn)矩負(fù)載、二次方率負(fù)載和恒功率負(fù)載三種工況下的調(diào)速關(guān)系模型。

1)恒轉(zhuǎn)矩負(fù)載調(diào)速關(guān)系模型。

恒轉(zhuǎn)矩負(fù)載設(shè)備有傳送帶、軋鋼機(jī)、提升機(jī)等，負(fù)載轉(zhuǎn)矩為定值，即T(g)=Tload=Tc，則

(16)

其中：

(17)

2)二次方率負(fù)載調(diào)速關(guān)系模型。

(18)

3)恒功率負(fù)載調(diào)速關(guān)系模型。

恒功率負(fù)載設(shè)備有造紙機(jī)及機(jī)床主軸等，負(fù)載轉(zhuǎn)矩與轉(zhuǎn)速成反比，即T(g)=Tload=9 550P/nout，則

(19)

運(yùn)用數(shù)值分析軟件，對(duì)以上3種工況下的調(diào)速模型進(jìn)行離散化求解，可得到其調(diào)速特性。

2 電磁場(chǎng)及調(diào)速特性仿真分析

為了驗(yàn)證電磁轉(zhuǎn)矩及調(diào)速關(guān)系的數(shù)學(xué)模型，本文運(yùn)用有限元軟件對(duì)SAAMC進(jìn)行三維建模與仿真分析。

2.1 三維模型建立

圖5為在有限元分析軟件中建立的SAAMC的三維模型，其結(jié)構(gòu)參數(shù)和材料屬性分別見表1、表2。三維模型建立后，對(duì)其進(jìn)行網(wǎng)格劃分及求解設(shè)置。

圖5 磁力耦合器三維模型Fig.5 3-D model of the magnetic coupler

2.2 氣隙磁場(chǎng)仿真分析

圖6為氣隙厚度為6 mm時(shí)耦合器永磁體的磁場(chǎng)強(qiáng)度云圖，可以發(fā)現(xiàn)永磁轉(zhuǎn)子的磁場(chǎng)強(qiáng)度整體上大于銅轉(zhuǎn)子磁感應(yīng)強(qiáng)度。永磁轉(zhuǎn)子上磁場(chǎng)強(qiáng)度在兩永磁體之間達(dá)到最大值，導(dǎo)體轉(zhuǎn)子上磁感應(yīng)強(qiáng)度在齒槽邊緣達(dá)到最大值。圖7為氣隙厚度為6 mm、輸入轉(zhuǎn)速1 200 r/min、轉(zhuǎn)差率10%時(shí)的瞬態(tài)磁感應(yīng)強(qiáng)度云圖，永磁轉(zhuǎn)子上磁感應(yīng)強(qiáng)度略低于永磁體的磁場(chǎng)強(qiáng)度，但分布規(guī)律基本一致。

圖6 永磁體的磁場(chǎng)強(qiáng)度云圖Fig.6 Magnetic field intensity nephogram of permanent magnet

圖7 瞬態(tài)磁感應(yīng)強(qiáng)度云圖Fig.7 Transient magnetic induction intensity nephogram

2.3 機(jī)械特性與功率特性仿真分析

SAAMC的結(jié)構(gòu)參數(shù)及工作條件確定時(shí)，將電磁轉(zhuǎn)矩與輸出轉(zhuǎn)速、轉(zhuǎn)差率之間的關(guān)系曲線(nout=f(T)或T=f(s))稱為機(jī)械特性曲線，將輸出功率與轉(zhuǎn)差率之間的關(guān)系P=f(s)稱為功率特性。圖8為輸入轉(zhuǎn)速1 200 r/min，氣隙厚度為1 mm下的機(jī)械特性曲線，當(dāng)負(fù)載轉(zhuǎn)矩小于啟動(dòng)轉(zhuǎn)矩Tst時(shí)，磁力耦合器啟動(dòng)。啟動(dòng)后，電磁轉(zhuǎn)矩先增大后減小，轉(zhuǎn)差率為sm時(shí)，電磁轉(zhuǎn)矩達(dá)到最大值Tm，即(Tm，sm)為磁力耦合器的最大轉(zhuǎn)矩點(diǎn)。從模擬結(jié)果可以發(fā)現(xiàn)不同氣隙厚度下，最大轉(zhuǎn)矩點(diǎn)的轉(zhuǎn)差率均為sm=15%(見圖10)。圖9為輸出功率隨轉(zhuǎn)差率變化的曲線，可見氣隙厚度為1 mm時(shí)，在轉(zhuǎn)差率sP1=11%處達(dá)到最大功率值Pm=20.35 kW，即(sP1，Pm)為氣隙厚度1 mm時(shí)的最大功率點(diǎn)，氣隙厚度為14 mm時(shí)，在sP2=13%處達(dá)到最大功率值Pn=2.26 kW，即(sP2，Pn)為氣隙厚度14 mm時(shí)的最大功率點(diǎn)。可見，磁力耦合器最大轉(zhuǎn)矩點(diǎn)的轉(zhuǎn)差率固定不變，最大功率點(diǎn)的轉(zhuǎn)差率隨著氣隙厚度的增大而略有增大，處于sP1～sP2范圍。且運(yùn)行轉(zhuǎn)差率小于最大轉(zhuǎn)矩點(diǎn)或最大功率點(diǎn)處轉(zhuǎn)差率時(shí)，轉(zhuǎn)矩或功率隨轉(zhuǎn)差率減小而減小的速度較快，反之則較慢。另外，由各曲線間的距離可以看出，最大轉(zhuǎn)矩值和最大功率值均隨氣隙厚度的增大呈非線性減小，減小速度先快后慢。所以需要較大轉(zhuǎn)矩和功率時(shí)，應(yīng)在較小工作氣隙下，選擇最大轉(zhuǎn)矩點(diǎn)或最大功率點(diǎn)附近的區(qū)間進(jìn)行調(diào)速。

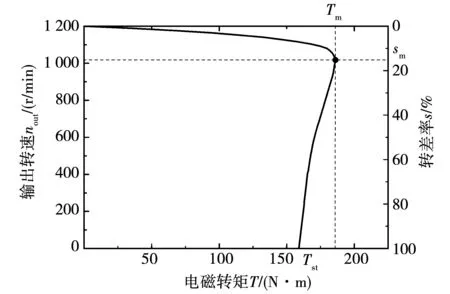
圖8 機(jī)械特性曲線Fig.8 Mechanical characteristic curve

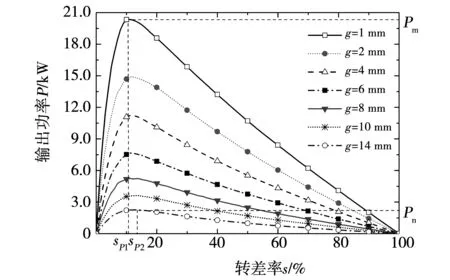
圖9 變氣隙下輸出功率隨轉(zhuǎn)差率變化曲線Fig.9 Variation curves of output power with slip rate under variable air gaps

2.4 調(diào)速特性仿真分析

圖10為恒轉(zhuǎn)矩負(fù)載下的調(diào)速特性曲線，可知輸出轉(zhuǎn)速區(qū)間為n0～nm時(shí)，耦合器穩(wěn)定運(yùn)行，其中nm為最大轉(zhuǎn)矩點(diǎn)(Tm，sm)處的轉(zhuǎn)速，點(diǎn)a～e屬于穩(wěn)定運(yùn)行點(diǎn)。若負(fù)載由T0增加為T1，將氣隙厚度由4 mm減小為2 mm即可以保持輸出轉(zhuǎn)速為n1不變，工作點(diǎn)由a點(diǎn)轉(zhuǎn)移到b點(diǎn)；若負(fù)載保持為T2不變，將氣隙厚度由1 mm增大到2 mm即可以將輸出轉(zhuǎn)速由n1調(diào)整到n2，工作點(diǎn)由c點(diǎn)轉(zhuǎn)移到d點(diǎn)。即磁力耦合器可以實(shí)現(xiàn)兩種模式的速度調(diào)控：其一為負(fù)載轉(zhuǎn)矩值變化時(shí)，改變氣隙厚度控制輸出轉(zhuǎn)速不變；其二為負(fù)載轉(zhuǎn)矩值不變時(shí)，改變氣隙厚度控制輸出轉(zhuǎn)速達(dá)到目標(biāo)值。

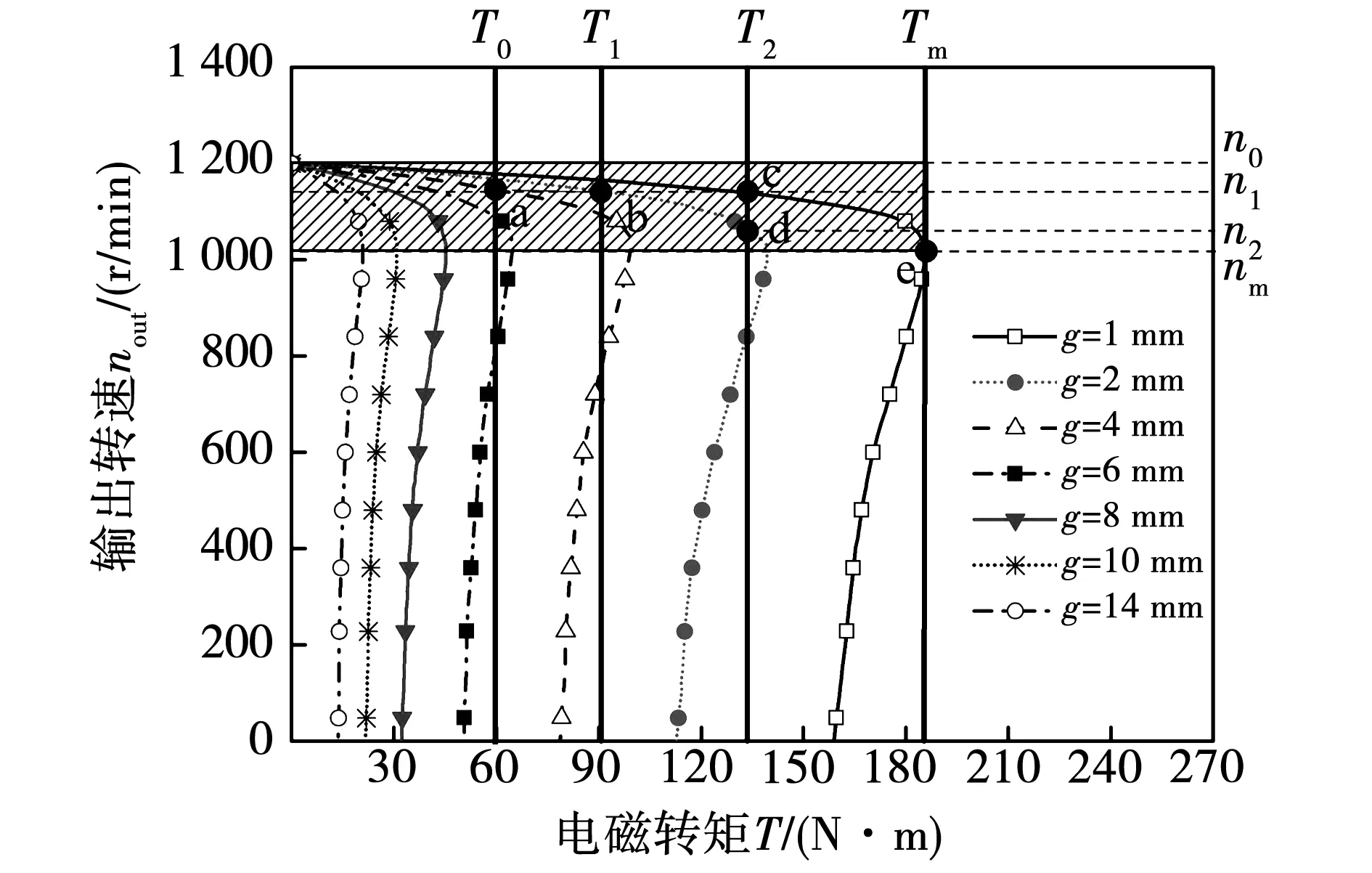
圖10 不同氣隙處恒轉(zhuǎn)矩負(fù)載調(diào)速特性曲線Fig.10 Speed-control characteristic curves under constant torque load at different air gaps

圖11為二次方率負(fù)載下調(diào)速特性曲線，系數(shù)為k1、k2及k3的二次方率負(fù)載曲線與不同氣隙厚度下的機(jī)械特性曲線的交點(diǎn)處均穩(wěn)定運(yùn)行。負(fù)載系數(shù)為k2=1.59×10-4時(shí)二次方率負(fù)載曲線與氣隙厚度為1 mm的機(jī)械特性曲線交于最大功率點(diǎn)N，此時(shí)調(diào)速區(qū)間為0～nk2，可達(dá)到最大功率，負(fù)載系數(shù)減小為k1時(shí)，調(diào)速區(qū)間增大為0～nk1，功率減小較快(如圖9)，負(fù)載系數(shù)增大為k3時(shí)調(diào)速區(qū)間減小為0～nk3，功率減小較慢。可見，以與最小工作氣隙的最大功率點(diǎn)相交的二次方率負(fù)載曲線的系數(shù)為臨界值，負(fù)載系數(shù)越小調(diào)速范圍越大，功率減小較快，適合小轉(zhuǎn)矩下的大范圍調(diào)速；負(fù)載系數(shù)越大，調(diào)速范圍越小，但功率減小較慢，適合大轉(zhuǎn)矩下的小范圍調(diào)速。

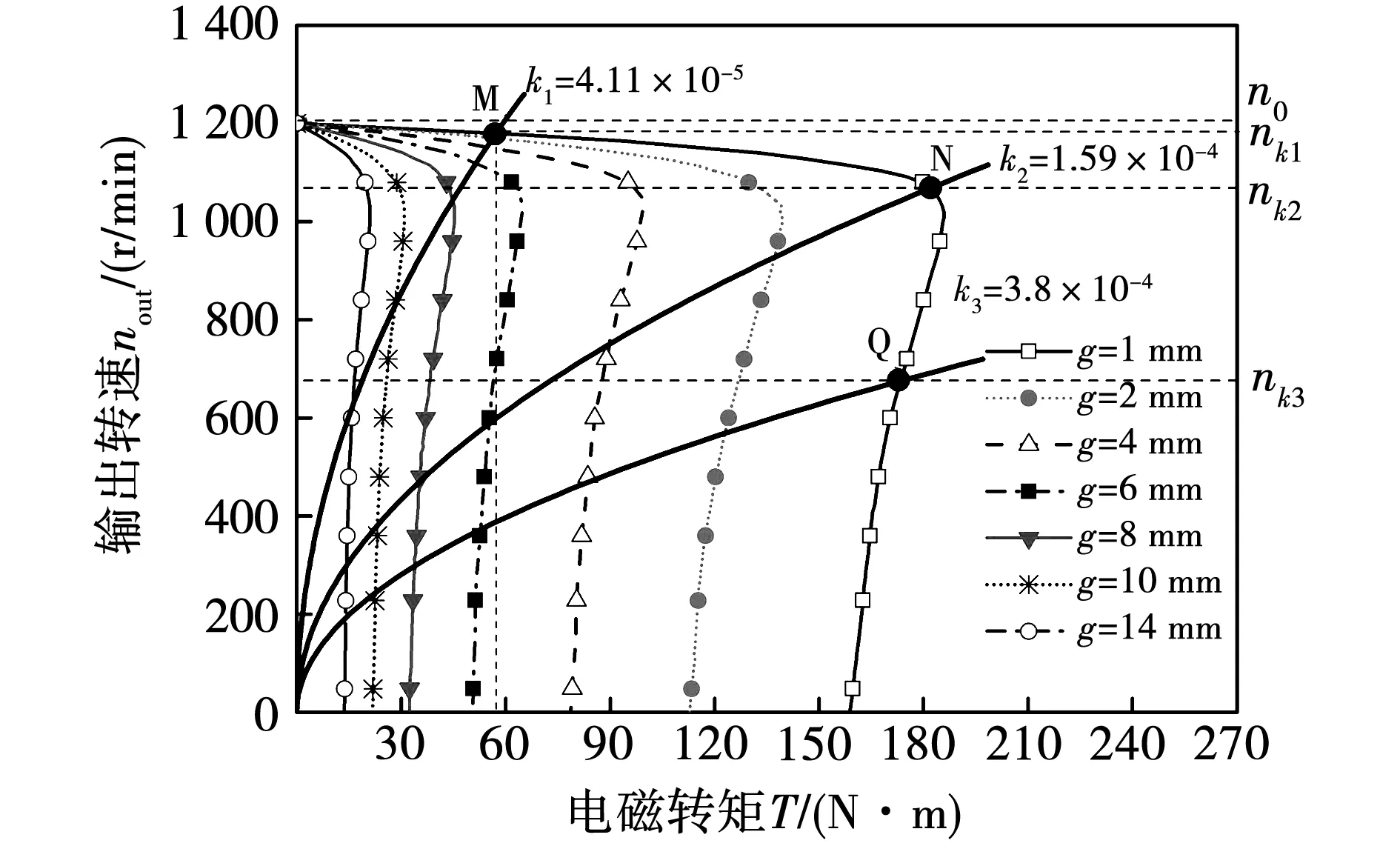
圖11 二次方率負(fù)載不同氣隙下調(diào)速特性曲線Fig.11 Speed-control characteristic curves under quadratic rate load at different air gaps

圖12為恒功率負(fù)載調(diào)速特性曲線，f～k為一定氣隙時(shí)的最大功率點(diǎn)。

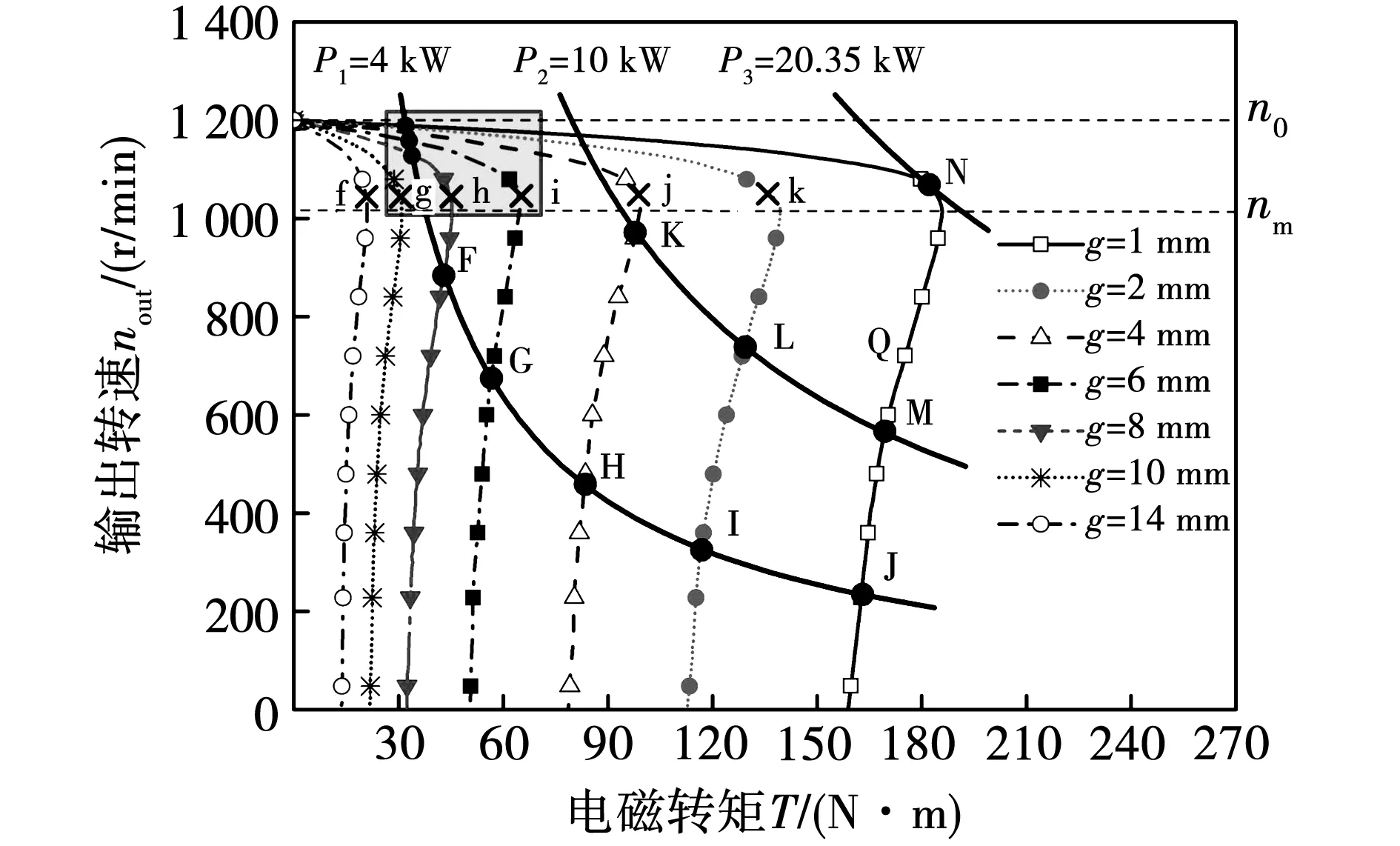
圖12 恒功率負(fù)載不同氣隙下調(diào)速特性曲線Fig.12 Speed-control characteristic curves under constant power load at different air gaps

圖13為圖12中方框處的放大圖，當(dāng)轉(zhuǎn)速大于最大功率點(diǎn)對(duì)應(yīng)的轉(zhuǎn)速時(shí)，磁力耦合器處于穩(wěn)定運(yùn)行區(qū)域。恒功率值為P1時(shí)，A～E點(diǎn)為穩(wěn)定運(yùn)行點(diǎn)，F(xiàn)～J點(diǎn)為不穩(wěn)定運(yùn)行點(diǎn)，調(diào)速區(qū)間為nP1～nP2，可進(jìn)行調(diào)速的氣隙范圍為1～8 mm。當(dāng)負(fù)載功率值為P2時(shí)，K～M點(diǎn)為不穩(wěn)定運(yùn)行點(diǎn)，此時(shí)可進(jìn)行調(diào)速的氣隙范圍減小為1～4 mm。當(dāng)負(fù)載功率值增大為P3時(shí)，負(fù)載曲線與氣隙厚度1 mm的機(jī)械特性曲線相切于最大功率值點(diǎn)N，僅有N點(diǎn)為穩(wěn)定運(yùn)行點(diǎn)，此時(shí)無法進(jìn)行調(diào)速。可見，負(fù)載功率值越大，可進(jìn)行調(diào)速的氣隙范圍越小，磁力耦合器可以帶動(dòng)的最大恒功率負(fù)載為P3=20.35 kW，與最小工作氣隙1 mm處的最大功率值(見圖9)相等。

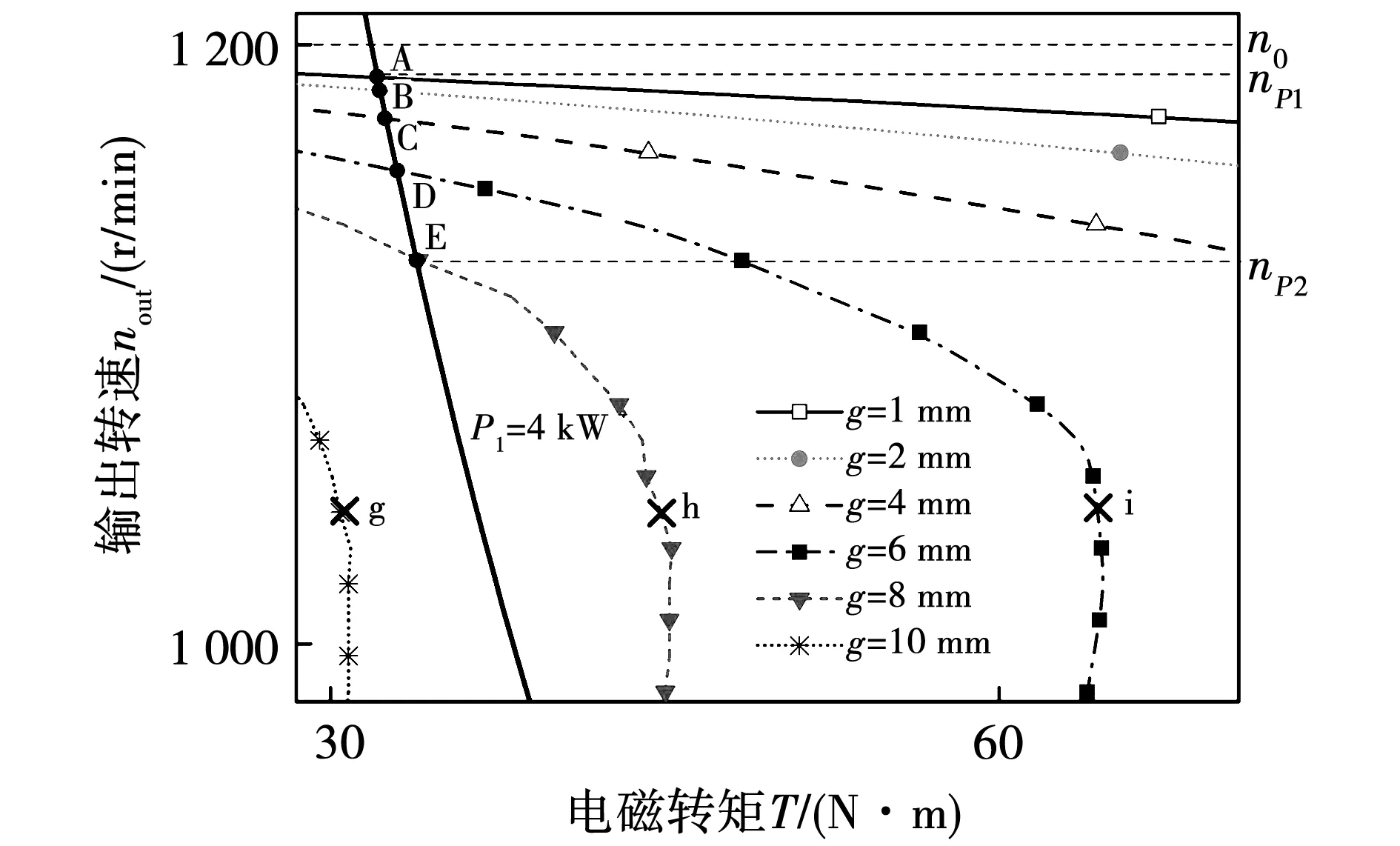
圖13 圖12中A～E處的局部放大圖Fig.13 A local enlargement at points A～E in Fig.12

3 實(shí)驗(yàn)驗(yàn)證

為進(jìn)一步驗(yàn)證電磁轉(zhuǎn)矩及調(diào)速關(guān)系的計(jì)算值與仿真值的準(zhǔn)確性，需對(duì)磁力耦合器的調(diào)速過程進(jìn)行實(shí)驗(yàn)驗(yàn)證，由于實(shí)驗(yàn)條件限制，僅對(duì)調(diào)速過程中的穩(wěn)態(tài)工作點(diǎn)進(jìn)行實(shí)驗(yàn)。

3.1 實(shí)驗(yàn)裝置

圖14為SAAMC的實(shí)驗(yàn)平臺(tái)。平臺(tái)的動(dòng)力源為5.5 kW的三相電機(jī)，通過變頻器控制其輸出轉(zhuǎn)速。JC型傳感器用于測(cè)量磁力耦合器輸入以及輸出端的轉(zhuǎn)矩和轉(zhuǎn)速，磁粉制動(dòng)器提供恒負(fù)載或風(fēng)機(jī)提供二次方率負(fù)載。實(shí)驗(yàn)過程中給定負(fù)載，改變氣隙厚度，測(cè)量不同氣隙厚度下的輸出轉(zhuǎn)速，得到氣隙厚度與輸出轉(zhuǎn)速和轉(zhuǎn)差率的關(guān)系曲線。

圖14 負(fù)載試驗(yàn)平臺(tái)Fig.14 Test platform with loads

3.2 實(shí)驗(yàn)結(jié)果及分析

圖15為磁力耦合器輸入轉(zhuǎn)速1 200 r/min，使用磁粉制動(dòng)器提供10 N·m恒轉(zhuǎn)矩負(fù)載時(shí)，不同氣隙下輸出轉(zhuǎn)速和轉(zhuǎn)差率的實(shí)驗(yàn)值、計(jì)算值及模擬值的對(duì)比圖，三者趨勢(shì)基本一致。但是，由于實(shí)驗(yàn)過程中存在摩擦、振動(dòng)以及測(cè)量誤差等不可避免的因素影響，實(shí)驗(yàn)值較計(jì)算值和模擬值偏小。圖16為磁力耦合器輸入轉(zhuǎn)速為1 100 r/min時(shí)，使用風(fēng)機(jī)提供系數(shù)為k=1.025×10-6二次方率負(fù)載時(shí)，不同氣隙厚度下輸出轉(zhuǎn)速、轉(zhuǎn)差率的實(shí)驗(yàn)值與計(jì)算值和模擬值的對(duì)比圖，當(dāng)氣隙厚度在6～14 mm時(shí)，三者趨勢(shì)基本一致，但當(dāng)氣隙厚度達(dá)到14 mm之后出現(xiàn)較大偏差。除上述不可避免的因素影響外，大氣隙下磁力耦合器帶載能力弱、受摩擦轉(zhuǎn)矩影響更大，也會(huì)引起較大偏差。可見，實(shí)驗(yàn)結(jié)果與計(jì)算、模擬結(jié)果在小氣隙范圍內(nèi)具有較好的一致性，而在二次方率負(fù)載下，當(dāng)氣隙厚度較大時(shí)，產(chǎn)生的偏差較大，但其偏差小于5%。

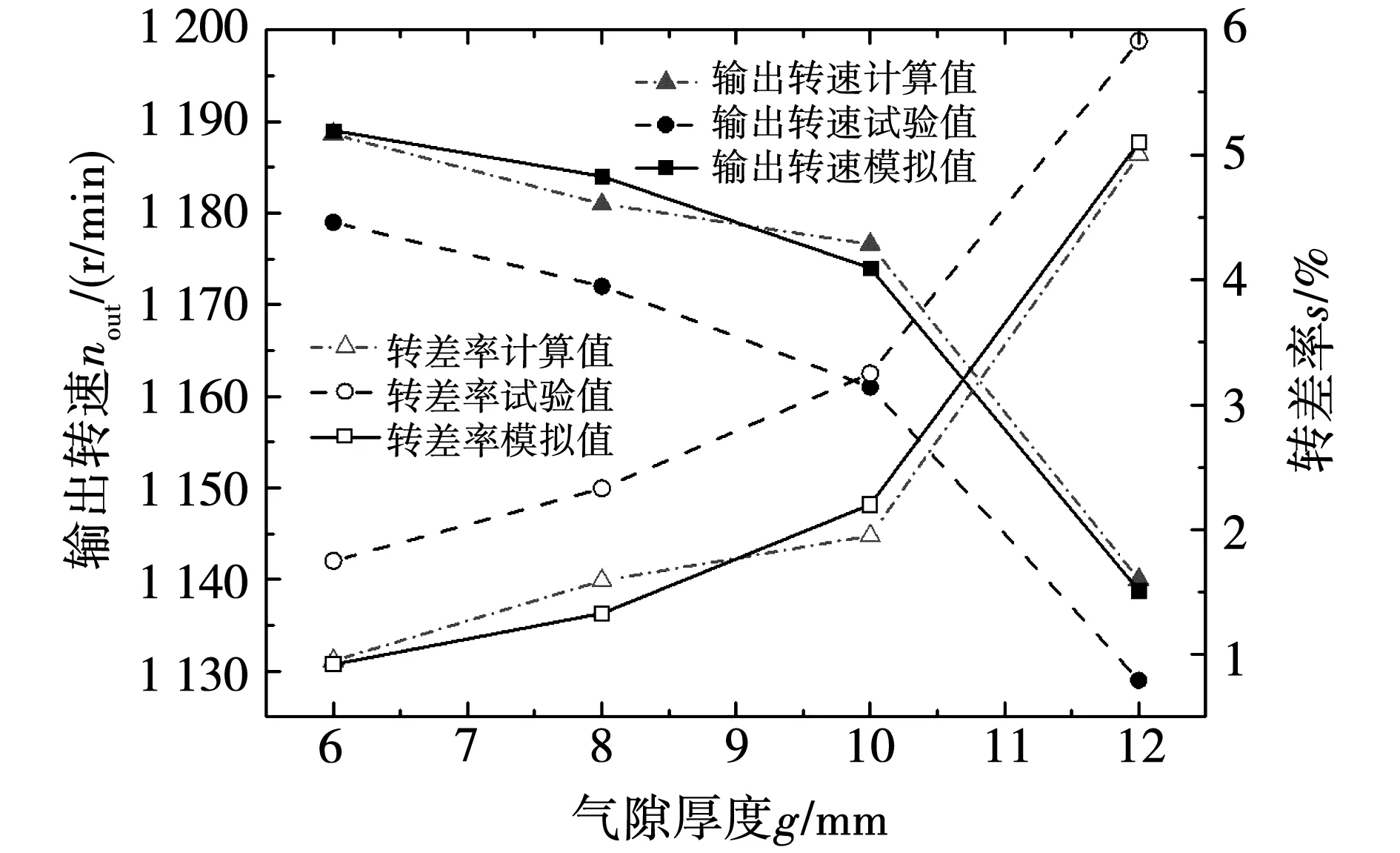
圖15 恒負(fù)載調(diào)速關(guān)系曲線對(duì)比Fig.15 Comparison of speed-control curves under constant load

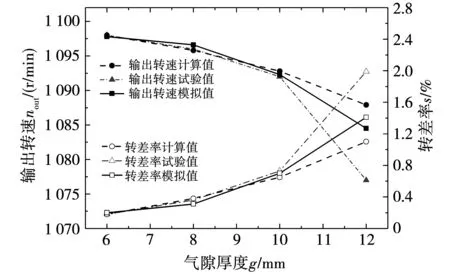
圖16 二次方率負(fù)載調(diào)速關(guān)系曲線對(duì)比Fig.16 Comparison of speed-control curves under quadratic rate load

4 結(jié) 論

1)運(yùn)用等效磁路法結(jié)合卡特系數(shù)，并考慮三維端部效應(yīng)，推導(dǎo)出SAAMC的電磁轉(zhuǎn)矩公式，建立了其轉(zhuǎn)速調(diào)控的計(jì)算模型。

2)通過有限元模擬確定最大轉(zhuǎn)矩點(diǎn)和最大功率點(diǎn)。可知，最大轉(zhuǎn)矩點(diǎn)的轉(zhuǎn)差率為定值，而最大功率點(diǎn)的轉(zhuǎn)差率隨著氣隙厚度的變化而略有變化，根據(jù)轉(zhuǎn)矩和功率隨轉(zhuǎn)差率及氣隙厚度的變化規(guī)律，可以合理選擇調(diào)速區(qū)間。

3)結(jié)合不同負(fù)載特性，確定了耦合器在三種不同負(fù)載工況下的調(diào)速范圍和調(diào)速特征。通過最大轉(zhuǎn)矩點(diǎn)，獲得了恒負(fù)載下的穩(wěn)定調(diào)速區(qū)間，并分析了兩種調(diào)速模式；根據(jù)最小氣隙的最大功率點(diǎn)確定二次方率負(fù)載的臨界值，劃分兩種調(diào)速范圍；通過最大功率點(diǎn)確定耦合器工作的最大恒功率負(fù)載和可調(diào)速的氣隙范圍。

4)通過數(shù)值計(jì)算、有限元分析及實(shí)驗(yàn)測(cè)試三者對(duì)比來驗(yàn)證理論分析及數(shù)值模擬的一致性，為磁力耦合器的智能調(diào)速和實(shí)際應(yīng)用提供理論參考。