基于GeoGebra設計與實現橢圓可視化動態課件

隨著現代信息技術對數學教學支撐能力的增強，教師的教學活動不再局限于用靜態的板書進行演示，用自然語言、符號語言解釋數學概念，也不再局限于用幻燈片演示，而是可以動態可視化展示，使課堂更有趣味性與探究性。在這種情境下學習，學生掌握知識更加牢固。數字化教學還能激發學生的求知欲以及探索、實踐的積極性。除了大眾所熟知的幾何畫板、超級畫板外，GeoGebra等數學繪圖軟件也被快速推廣應用，這些工具的適當使用有利于提高教學效率。

一、GeoGebra在幾何教學中的獨特優勢

目前，多數教師執教橢圓這一教學內容時還是利用PPT進行新課的講授。用PPT制作的課件，在動態性、實時操作性上有一定的缺陷，不能實現信息技術與課堂的整合。例如，教師只能借助其他平臺制作動畫，再將動畫錄制成視頻引入PPT中播放，無法實現動畫應有的交互性。有些畫板軟件囿于版權以及對理論知識要求高等原因，用起來比較煩瑣。GeoGebra軟件具有開源、可視化程度高、簡單易學等特點，逐漸獲得教師認可。在人教A版高中數學選擇性必修第一冊教材中，運用的軟件正是GeoGebra。GeoGebra是什么？這個單詞由Geo和Gebra組成，也就是geometry（幾何）和algebra（代數）。顧名思義，它是一款結合幾何、代數甚至微積分的動態數學軟件。GeoGebra在繪制動態圖以及教學演示方面有其獨特優勢，可以作為可視化教學的工具。

筆者以橢圓為例，借助GeoGebra軟件，探究動態課件的設計與實現方法，建立可視化與抽象的聯系，以期突破“意會”與“言傳”的障礙，實現高中數學課堂可視化教學，提升學生直觀想象等數學核心素養。

二、橢圓動態課件的設計

（一）設計目標

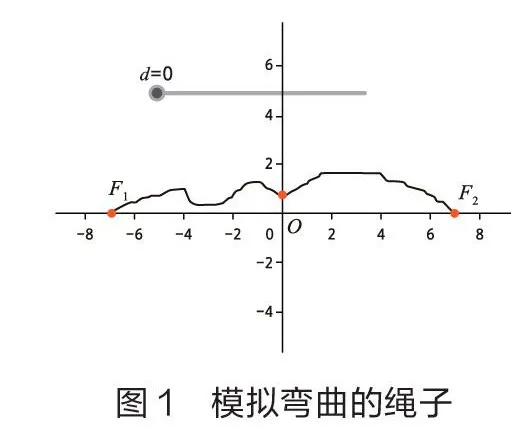
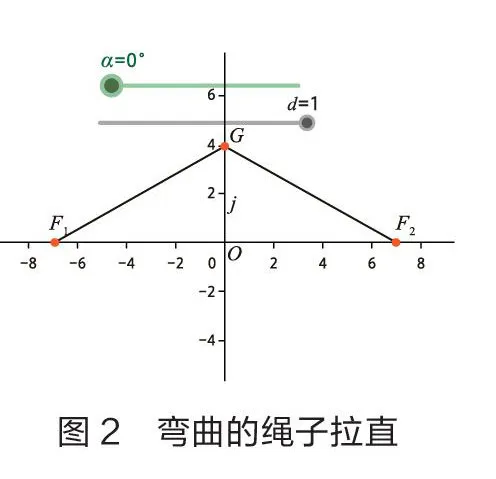
首先，借助GeoGebra實現人教A版高中數學選擇性必修第一冊第105頁中的探究，即通過GeoGebra軟件將兩端被固定的一條彎曲繩子拉直。在彎曲的繩子上取一點，將繩子拉直后，移動這一點，繪制點的軌跡。通過這一動態過程展示橢圓的形成過程。

其次，利用GeoGebra的相關功能動態呈現橢圓的一些基本性質，如、的范圍、對稱性、頂點、離心率等。課堂上，通過GeoGebra實現動態的演示，引導學生思考，做出猜想，最后借助GeoGebra軟件進行論證。

在這過程中，教師應用GeoGebra表格記錄功能以及跟蹤功能，開展探究性教學，引導學生思考參數、、是如何影響橢圓的扁平程度的，進而引出離心率概念，并探究離心率數值的大小如何影響橢圓扁平程度。

（二）難點突破

需要處理的問題：如何實現任意曲線的繪制;如何實現曲線拉直這一過程;曲線拉直后如何繪制橢圓的軌跡。

制作過程中需要用到一些指令，如曲線、軌跡、位似、如果等，以及一些工具，如畫筆、折線、滑動條、復選框等，運用這些指令來解決問題，這是需要突破的難點。

1.曲線的繪制 ：使用GeoGebra的畫筆工具，自由繪制想要的曲線，模擬繩子。

2.曲線拉直的實現：使用折線工具，繪制橢圓焦點與橢圓上一點的折線，在曲線上取一點，過該點作軸的垂線與折線的交點;建立滑動條，利用位似指令實現曲線拉直的動畫過程，并通過滑動條實現這一過程的實時控制。

3.橢圓軌跡的繪制：利用曲線指令以及滑動條實現簡單的動態繪制，再利用一些腳本指令，如啟動動畫、賦值等，優化動畫的展示過程。

三、橢圓動態課件的GeoGebra實現

（一）實現橢圓形成的動態過程

人教A版高中數學選擇性必修第一冊教材對橢圓的定義是這樣的：將平面內與兩個定點、的距離的和等于常數（大于丨丨）的點的軌跡叫作橢圓（ellipse）。在教學過程中，學生很難進行直觀想象;囿于常規教具，也很難實現這一動態作圖過程。教師借助GeoGebra軟件，制作動畫來演示這一過程，讓學生對橢圓的第一定義有更加直觀的認識。

繪圖目標：彎曲的繩子兩端被固定，在繩子上的取一點，將繩子拉直，拉之后進行橢圓的動態繪制。

繪制步驟如下：

1.利用滑動條工具，建立滑動條、，其區間分別設置為（0，10）和（0，），增量均為1。

2.在輸入框中輸入 ：^2/^2+^2/^2= 1，得到橢圓方程。

3.在輸入框中輸入：_1=焦點（），得到焦點和。

4.在輸入框中輸入：頂點（），得到橢圓的4個頂點分別為、、、。

5.用畫筆工具，以為起點，為終點，描一段彎曲的繩子，得到stroke1。

6.用折線工具，依次連接、、、，得到折線。

7.利用描點工具，在stroke1上描點，得到點。

8.在輸入框中輸入：交點（垂線（， 軸）， ），得到點。

9.利用滑動條工具，建立滑動條，其區間設置為（0，1），增量默認不填，動畫設置為“遞增（一次）”。

10.在輸入框中輸入：位似（， ， ），得到點。

11.在輸入框中輸入：軌跡（， ），得到軌跡loc1。

12.利用復選框工具，命名為隱藏輔助線，在繪圖區中分別點擊筆觸stroke1、點、折線。

13.利用滑動條工具，建立角度滑動條，將其區間設置為（0°，360°），增量為1°;將動畫一欄速度設置為3，遞增（一次）。

14.在輸入框中輸入：曲線（cos（），sin（），，90°，90°+），得到參數曲線。

15.在輸入框中輸入：（ + 90°），得到點。

16.利用復選框工具，以標題為頂點，在代數區單擊頂點、、、，實現通過復選框控制頂點的出現。

17.右擊滑動條，選擇屬性，在腳本更新中輸入“啟動動畫[，==1]”。

18.右擊滑動條，選擇屬性，高級顯示條件中輸入：==1。腳本中更新時輸入：如果（ == 0，賦值[，0°]）。

19. 利用折線工具，依次連接點、、、，得到折線。

20.按住Ctrl鍵，在代數區單擊點、折線，右鍵屬性，在高級顯示條件中輸入：=1。

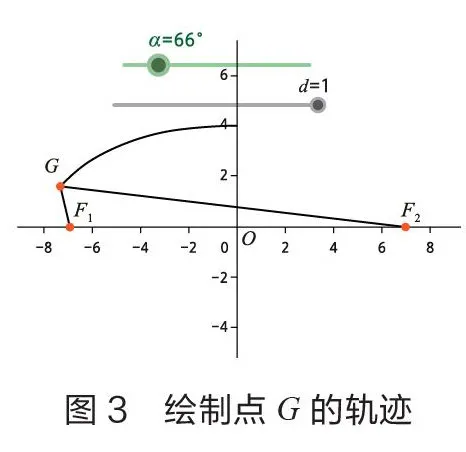
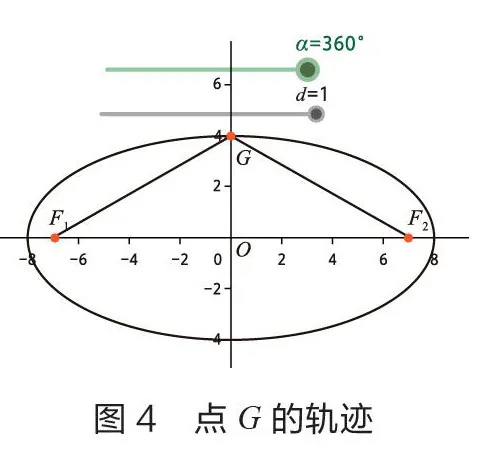
按以上步驟，繪圖完畢。此時可以通過控制滑動條，實現橢圓的動態繪制過程。當=0，是一條彎曲的“繩子”，的值從0到1的過程中，是實現“繩子”被拉直的過程。當=1時滑動條就會自動啟動，實現模擬橢圓的繪制過程（如圖1至圖4）。

（二）實現橢圓的簡單幾何性質的動態演示

教學中，大部分教師使用PPT講授橢圓的簡單幾何性質時會參考一個表格（見表1）進行動態課件的展示。但是這樣操作無法讓學生獲得直觀的感受。GeoGebra的應用為解決這一問題提供了便利，它不僅支持PPT中的動畫功能，而且可以支持教師控制參數實現動畫變化，使抽象的知識變得直觀，利于學生更好地理解和記憶。

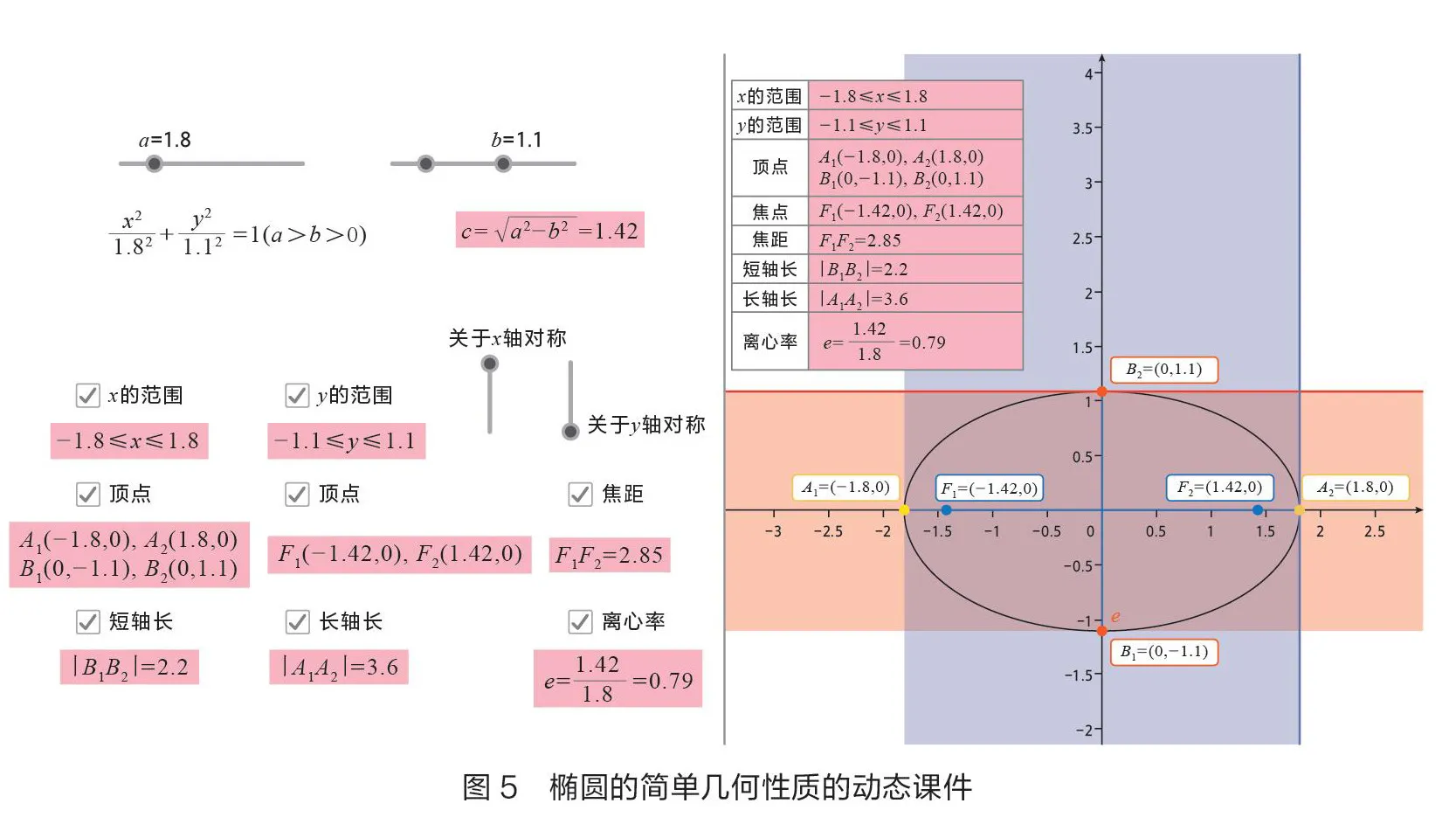
表2呈現的是橢圓的簡單幾何性質動態課件的實現結果。教師在GeoGebra 軟件的輸入框中輸入表2定義欄中的內容后，通過復選框工具、文本工具以及表格文本指令，可以實現幾何性質的動態演示。教師通過控制滑動條、改變橢圓的各個參數，從而改變橢圓的形狀;使用復選框工具，可實時控制每個基本性質的顯示與隱藏。最后，所有的基本性質被匯總在一個表格里系統地呈現。

動態課件的整體展示如圖5所示，左側是控制區，也是數值顯示區，右側則是圖象顯示區與表格匯總區域。除了可以通過復選框控制基本性質的展示外，教師還可以通過名為“關于軸對稱”“關于軸對稱”的兩個滑動條，控制關于橢圓對稱性的動畫演示。

教師還可以利用GeoGebra的“顯示跟蹤”功能，通過改變、的值，對橢圓的軌跡進行跟蹤;同時引導學生思考橢圓的扁平程度與參數、、之間的關系。教師借此引出離心率，讓學生結合剛剛的動畫演示教學，總結離心率與橢圓的扁平程度規律。

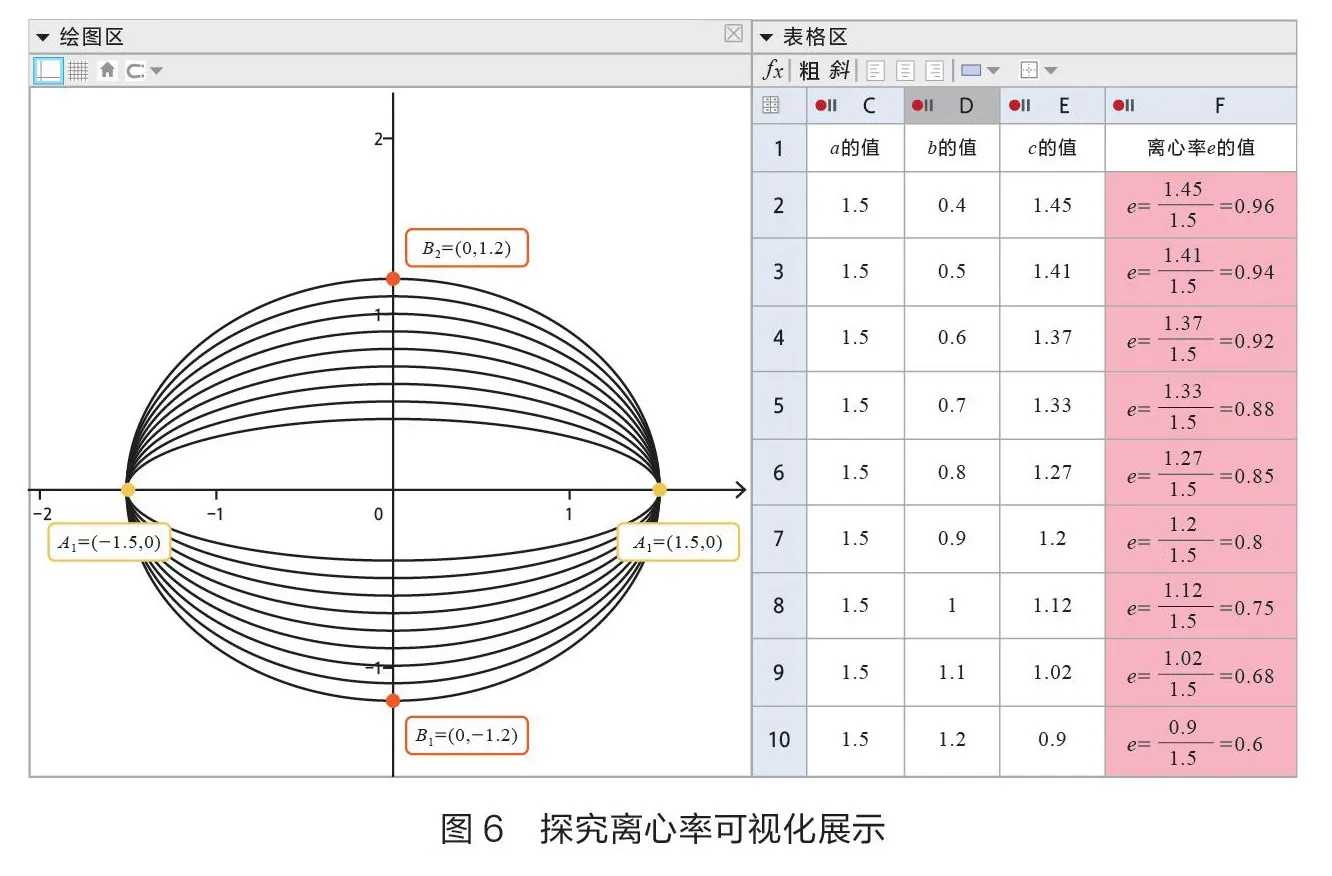
教師可以控制滑動條，利用GeoGebra自動記錄數值的功能以及“跟蹤功能”，實現數形結合的可視化展示（如圖6）。隨著值逐漸增大，離心率變小，橢圓就越圓。這有助于學生證明其猜想或推論正確與否。

在高中數學的教學中，用GeoGebra軟件制作可視化動態課件有著廣闊的天地。教師科學應用信息工具可實現抽象概念可視化，解題可視化，教學可視化。利用可視化的動態課件可以創設情境，讓學生記錄、觀察，條件允許的情況下還可以讓學生動手操作。軟件演示可為學生猜想、證明提供一定的幫助。教師在此基礎上引導學生進行論證，得出結論，這樣效果更好。基于GeoGebra制作的動態課件可用于可視化教學，引導學生思考。可視化交互有利于學生交流思想，主動構建知識網絡結構，引發其探究、論證。學生經歷解決問題的全過程，對知識的學習會更加扎實，成效會更顯著。

（作者系廣東省廣州市亞加達外國語高級中學教師）

責任編輯：祝元志