應(yīng)用動(dòng)態(tài)數(shù)學(xué)軟件探究鉛球投擲問題

一、問題的提出

物理是一門基于實(shí)驗(yàn)探究物體運(yùn)動(dòng)規(guī)律的學(xué)科，也是一門經(jīng)常應(yīng)用數(shù)學(xué)知識(shí)的學(xué)科。多數(shù)高中生數(shù)學(xué)基礎(chǔ)不扎實(shí)且跨學(xué)科知識(shí)融合能力較弱，學(xué)習(xí)物理學(xué)科內(nèi)容時(shí)，往往不能有效應(yīng)用數(shù)學(xué)知識(shí)解決物理問題，更談不上感受科學(xué)之美。例如，被投擲的鉛球在空中的運(yùn)動(dòng)屬于斜拋運(yùn)動(dòng)，也是高中生常見的一種拋體運(yùn)動(dòng)。探究不同條件下投擲鉛球的最優(yōu)方案，涉及鉛球被投擲時(shí)的初速度大小、拋出點(diǎn)高度和拋出角等因素，如果應(yīng)用高等數(shù)學(xué)知識(shí)求解極值來探究，顯然超出高中生的數(shù)學(xué)能力范疇，也不利于學(xué)生理解。面對(duì)物理和數(shù)學(xué)兩門學(xué)科，學(xué)生通常感到公式多、抽象化難理解。如何走出困境？高中生對(duì)動(dòng)態(tài)的、圖象化的情境更感興趣。將問題解決過程可視化無疑是一種有益的嘗試。

當(dāng)前，信息技術(shù)為教育高度賦能，功能各異的軟件憑借各自特色技術(shù)融入教學(xué)之中。例如，GeoGebra是一款跨平臺(tái)動(dòng)態(tài)數(shù)學(xué)軟件，它不僅提供了針對(duì)幾何、代數(shù)、表格、圖形、統(tǒng)計(jì)和微積分等對(duì)象的強(qiáng)大分析功能，而且允許用戶借助電腦端、網(wǎng)頁在線使用，還支持平板電腦等移動(dòng)終端應(yīng)用。用戶應(yīng)用GeoGebra可創(chuàng)建各種復(fù)雜函數(shù)，并通過2D和3D的方式實(shí)時(shí)動(dòng)態(tài)化展示函數(shù)的變化情況，通過交互操作實(shí)現(xiàn)互動(dòng)功能。

拋體運(yùn)動(dòng)是高中物理課程中學(xué)生遇到的第一種曲線運(yùn)動(dòng)。學(xué)生在系統(tǒng)學(xué)習(xí)了勻速直線運(yùn)動(dòng)和勻變速直線運(yùn)動(dòng)后，首次綜合運(yùn)用所學(xué)知識(shí)解決復(fù)雜運(yùn)動(dòng)。各種版本的高中物理教材均詳細(xì)探究了平拋運(yùn)動(dòng)這種特殊的拋體運(yùn)動(dòng)，但學(xué)生在日常生活中更多遇到的是初速度與水平方向有一定夾角的斜拋運(yùn)動(dòng)，如投擲出的鉛球在空中的運(yùn)動(dòng)。如何根據(jù)不同個(gè)體特征精準(zhǔn)設(shè)定最優(yōu)投擲參數(shù)，對(duì)于學(xué)習(xí)了平拋運(yùn)動(dòng)知識(shí)后躍躍欲試的高中生而言，這是極具誘惑力的嘗試，也是一個(gè)頗具挑戰(zhàn)難度的研究性學(xué)習(xí)課題。

二、應(yīng)用GeoGebra研究鉛球的投擲問題

（一）鉛球運(yùn)動(dòng)過程的理論分析

在忽略空氣阻力的情況下，被投擲的鉛球在空中的運(yùn)動(dòng)可以分解為水平方向上的勻速直線運(yùn)動(dòng)和豎直方向上的勻變速直線運(yùn)動(dòng)。

根據(jù)運(yùn)動(dòng)學(xué)公式，鉛球在水平方向的位移和豎直方向上的位移分別如下（式1和式2）。

= cos （1）

=+ sin - ² （2）

將式1和式2聯(lián)立消去時(shí)間，得到如下表達(dá)式（式3）。

=+ tan - ² （3）

當(dāng)鉛球落地時(shí)，其豎直方向上位移=0，即有

+ tan - ² = 0 （4）

通過求根公式

= （5）

可得鉛球的投擲距離為

= （6）

分析式6后發(fā)現(xiàn)，決定鉛球投擲距離的因素包括拋出時(shí)初速度、拋出角度和拋出點(diǎn)高度。

如何求解鉛球投擲距離最遠(yuǎn)的參數(shù)條件？如果繼續(xù)從數(shù)學(xué)理論角度推導(dǎo)是不可信的，因?yàn)橐玫礁叩葦?shù)學(xué)知識(shí)會(huì)超出中學(xué)生的理解范疇，還不夠直觀、生動(dòng)。

（二）鉛球投擲參數(shù)的可視化分析

筆者打開GeoGebra的圖形計(jì)算器后，新建兩個(gè)滑動(dòng)條，分別用來控制鉛球拋出時(shí)的初速度和高度，綜合考慮高中生所處年齡段特點(diǎn)和參考運(yùn)動(dòng)員投擲鉛球的數(shù)據(jù)^[1]，輸入命令定義變量：

=slider（0，13，1）

=slider（1.5，2.5，0.1）

上面命令中用到了GeoGebra內(nèi)置的slider命令，三個(gè)參數(shù)分別是最小值、最大值和步長(zhǎng)。

接著定義函數(shù)（式7）：

（）= （7）

式（7）中取重力加速度=9.8 m/s²，其中為拋出角，在右上角符號(hào)為度（在函數(shù)定義過程中通過快捷鍵“Alt+O”實(shí)現(xiàn)）。這里，GeoGebra用度為單位運(yùn)算，否則軟件默認(rèn)采用弧度制單位。為使GeoGebra繪制的函數(shù)圖象與實(shí)際相符，需要將的取值范圍規(guī)定為小于等于90°。命令如下：

L1（）=if（0≤≤90，L（））

此時(shí)，繪圖區(qū)出現(xiàn)圖1所示效果。拖動(dòng)圖中的任意一個(gè)滑動(dòng)條或點(diǎn)擊繪圖區(qū)左下角的播放（暫停）按鈕后，GeoGebra實(shí)時(shí)動(dòng)態(tài)展示不同初速度、拋出角（以自變量表示）和拋出高度參數(shù)下的鉛球投擲距離。

觀察圖1后發(fā)現(xiàn)，在拋出高度和初速度均不變的情況下，鉛球的拋出角對(duì)投擲距離影響較大，且函數(shù)圖象存在極值點(diǎn)，因此對(duì)于特定的投擲者而言，需要根據(jù)自身特點(diǎn)選擇合適的拋出角（即最優(yōu)拋出角）投擲鉛球。

按分析物理運(yùn)動(dòng)圖象的習(xí)慣，師生可以進(jìn)一步從函數(shù)圖象的縱軸截距、橫軸截距和曲線斜率等方面分析鉛球的投擲問題。在圖1中，縱軸截距代表拋出角為0°時(shí)的投擲距離，這時(shí)斜拋運(yùn)動(dòng)就回歸到了教材中提及的平拋運(yùn)動(dòng)。橫軸截距意味著拋出角等于90°，斜拋運(yùn)動(dòng)就變成豎直上拋運(yùn)動(dòng)。這樣學(xué)生對(duì)鉛球的投擲距離為零就不難理解了。另外，將圖1中函數(shù)圖象的切線斜率定義為= ，可以發(fā)現(xiàn)在小角度或大角度情況下拋出鉛球時(shí)斜率較大，意味著在這兩種情況下，拋出角的改變將更為明顯影響鉛球的投擲距離，這進(jìn)一步佐證了優(yōu)化拋出角投擲鉛球的重要性。

鉛球被擲出后，初速度對(duì)投擲距離的影響是否明顯呢？為了直觀分析此問題，筆者控制參數(shù)不變，拖動(dòng)與初速度相應(yīng)的滑動(dòng)條，同時(shí)通過右鍵菜單選中“顯示軌跡”。GeoGebra隨即繪制出不同初速度下鉛球投擲距離與拋出角的函數(shù)圖象（如圖2所示，=2 m，初速度從=0 m/s至=13 m/s，間隔1 m/s繪制圖象，分別對(duì)應(yīng)圖中由低到高的各條曲線）。

分析圖2后發(fā)現(xiàn)，在拋出點(diǎn)高度不變的情況下，投擲鉛球時(shí)的初速度對(duì)投擲距離的影響也非常明顯，且在任意給定的同一拋出角條件下，初速度越大，投擲距離越遠(yuǎn)。另外，圖中各條函數(shù)曲線的極值點(diǎn)是隨初速度變化而變化的，這意味著最優(yōu)拋出角并不是恒定的，其隨著初速度的增大而變大，不過當(dāng)初速度增大到一定值時(shí)，最優(yōu)拋出角將趨于恒定。以拋出點(diǎn)高度為2 m為例，最優(yōu)拋出角最終將趨于42°。學(xué)生認(rèn)識(shí)到：運(yùn)動(dòng)員在日常訓(xùn)練投擲鉛球的過程中，不應(yīng)一味地重視對(duì)鉛球拋出角度的控制，還應(yīng)該通過體能訓(xùn)練和肢體動(dòng)作協(xié)調(diào)等方法給予鉛球足夠的初速度。

對(duì)圖2進(jìn)一步分析后發(fā)現(xiàn)，圖中各條函數(shù)曲線與縱軸的交點(diǎn)是等間距的。已知函數(shù)圖象與縱軸相交時(shí)代表鉛球的斜拋運(yùn)動(dòng)回歸到平拋運(yùn)動(dòng)，根據(jù)平拋運(yùn)動(dòng)知識(shí)，可計(jì)算投擲距離（式8）。

= （8）

顯然，在鉛球拋出高度相同、初速度等間隔變化的情況下，函數(shù)圖象與縱軸交點(diǎn)必然等間距分布。通過討論，學(xué)生不僅進(jìn)一步熟悉平拋運(yùn)動(dòng)知識(shí)，而且切身感受到學(xué)以致用的樂趣。另外，對(duì)于其他拋出角（0°<<90°）條件，函數(shù)圖象之間的間距均是先增大后減小，且函數(shù)切線的斜率除極值點(diǎn)外均整體變大，這也進(jìn)一步論證了鉛球拋出初速度對(duì)投擲距離有極大影響。

拋出角度和初速度兩個(gè)因素對(duì)鉛球的投擲距離影響顯著。為了進(jìn)一步提升投擲成績(jī)，是否有必要選拔高個(gè)子且手臂長(zhǎng)的運(yùn)動(dòng)員投擲鉛球呢？拖動(dòng)與拋出點(diǎn)高度相應(yīng)的滑動(dòng)條，GeoGebra自動(dòng)繪制出如圖3所示的不同拋出高度下的投擲距離函數(shù)圖象（初速度設(shè)定為=13 m/s，=1.5 m至=2.5 m，間隔0.2 m繪制圖象，分別對(duì)應(yīng)圖中由低到高的各條曲線）。

分析圖3后發(fā)現(xiàn)，隨著拋出點(diǎn)高度的增加，各個(gè)拋出角度下鉛球的投擲距離均有所增加，但差異并不明顯。此外，圖3中各條函數(shù)曲線的極值點(diǎn)會(huì)隨著拋出點(diǎn)高度的增加向左側(cè)偏移，這代表最優(yōu)拋出角會(huì)隨拋出點(diǎn)高度的增加而變小。

按物理中常用的“整體法”，圖3中各條函數(shù)曲線可整合命名為“函數(shù)曲線帶”。似乎這條“函數(shù)曲線帶”的寬度隨著拋出角的增大而變窄。為了驗(yàn)證此結(jié)論，在GeoGebra中命名新函數(shù)△ （）并計(jì)算圖3中這條“函數(shù)曲線帶”的寬度（因公式較長(zhǎng)，在此略），并通過GeoGebra繪制出函數(shù)圖象，效果如圖4所示。

學(xué)生分析圖4后確認(rèn)：隨著拋出角的增大，“函數(shù)曲線帶”的寬度確實(shí)在變窄。“函數(shù)曲線帶”的寬窄代表在初速度和拋出角均相同的情況下，在兩種極端拋出高度下分別投擲鉛球的投擲距離之差，由于圖4中函數(shù)的最大值在2 m左右，實(shí)際投擲鉛球時(shí)具有一定拋出角，且對(duì)于特定的投擲群體而言，實(shí)際投擲鉛球時(shí)其拋出點(diǎn)高度的差異基本不大，因此有理由相信鉛球投擲人員的身高和臂長(zhǎng)對(duì)鉛球投擲距離的影響小于1 m。

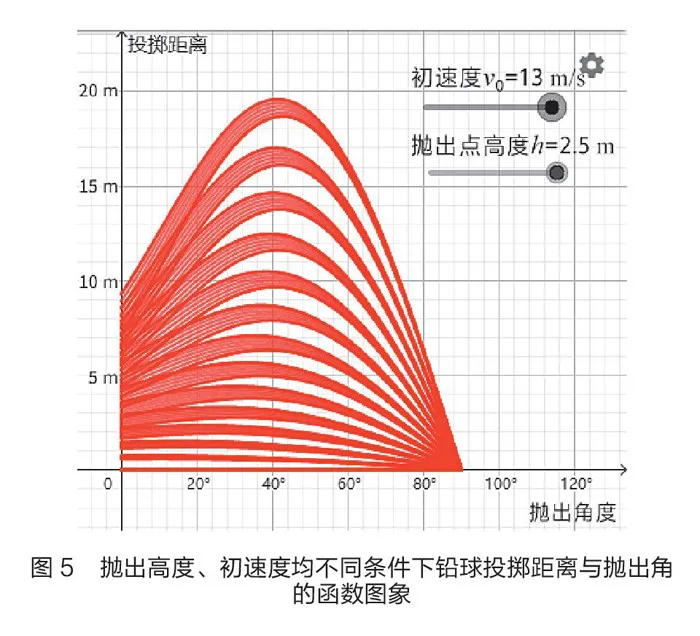
為了讓以上結(jié)論更具說服力，筆者同時(shí)拖動(dòng)與拋出點(diǎn)高度和初速度相應(yīng)的滑動(dòng)條，通過GeoGebra繪制一系列不同初速度且不同拋出高度下的投擲距離函數(shù)圖象（如圖5）。

在圖5中，同一初速度、不同拋出高度的函數(shù)曲線集中在一起成帶狀分布，隨著初速度增加，相應(yīng)的“函數(shù)曲線帶”依次向上排布，且在同一條“函數(shù)曲線帶”中的各條函數(shù)曲線均隨著拋出點(diǎn)高度的增加而依次從低到高分布。分別辨析圖5中各條“函數(shù)曲線帶”，發(fā)現(xiàn)在圖4中分析得到的結(jié)論同樣成立。

綜合以上分析，學(xué)生得到以下啟示：其一，為確保鉛球的投擲距離最遠(yuǎn)，讓鉛球獲得足夠大的初速度是關(guān)鍵，這不僅需要運(yùn)動(dòng)員的自身強(qiáng)大機(jī)體力量作為根基，而且需要通過合理的加速方式提高鉛球脫手時(shí)的初速度;其二，運(yùn)動(dòng)員在保證鉛球獲得最大初速度的基礎(chǔ)上，應(yīng)結(jié)合自身身高、臂長(zhǎng)和投球姿勢(shì)等因素確定鉛球的拋出點(diǎn)高度，然后基于前面的初速度和拋出點(diǎn)高度決定自身專屬的最優(yōu)拋出角。

高中生投擲鉛球初速度為5.6～8.2 m/s、鉛球拋出點(diǎn)高度處于1.7～2.0 m^[2]。筆者借助GeoGebra通過函數(shù)圖象讀取得到相應(yīng)的最優(yōu)拋出角分布在33.7°（=5.6 m/s，=2.0 m）至39.3°（=8.2 m/s，=1.7 m）之間，鉛球的最遠(yuǎn)投擲距離分布在4.8～8.39 m。對(duì)于不同個(gè)體條件下的具體最優(yōu)拋出角，將相應(yīng)數(shù)據(jù)輸入GeoGebra中即可計(jì)算得到。

三、總結(jié)與展望

本案例中，筆者借助GeoGebra軟件，以可視化分析的方式研究了鉛球投擲距離的函數(shù)圖象。師生通過研究發(fā)現(xiàn)：鉛球的投擲距離受拋出角度和初速度影響較大，受拋出點(diǎn)高度影響較小。

為取得更好的投擲鉛球成績(jī)，運(yùn)動(dòng)員應(yīng)意識(shí)到最佳拋出角的存在及其重要意義，還應(yīng)該注意到最佳拋出角是隨著鉛球的初速度和拋出點(diǎn)高度的變化而動(dòng)態(tài)變化的。運(yùn)動(dòng)員只有動(dòng)態(tài)把握這些變化規(guī)律，才能在體育競(jìng)技中不斷挑戰(zhàn)自我。

運(yùn)動(dòng)員在投擲鉛球時(shí)，可能還需要考慮空氣阻力的影響。這有待今后進(jìn)一步研究、完善。

需要強(qiáng)調(diào)的是，GeoGebra作為一款功能強(qiáng)大的動(dòng)態(tài)分析軟件，各種功能的應(yīng)用無法窮舉，未被文獻(xiàn)記載的方法，唯有使用者在日常學(xué)習(xí)和生活中不斷發(fā)掘，探索建立數(shù)學(xué)模型，并做可視化分析，才能在荊棘之路上一往無前。

參考文獻(xiàn)

[1] 王倩，周華鋒，劉茂輝，鮑偉.對(duì)兩名不同水平男子鉛球選手投擲技術(shù)的生物力學(xué)分析[J].北京體育大學(xué)學(xué)報(bào)，2007（3）：404-406.

[2] 盧飚，朱行建.推鉛球出手角：高中生的視角[J].物理教師，2013（4）：55-56.

（作者系貴州省六盤水市民族中學(xué)高級(jí)教師）

責(zé)任編輯：祝元志