磁體與運動導體相互作用的實驗研究

翦知漸，謝 中，周艷明

(湖南大學 物理與微電子科學學院 大學物理實驗中心，湖南 長沙 410082)

相對運動的非磁性導體與永磁體(或其他磁場)之間因電磁感應存在相互作用，研究這種相互作用對了解感應電機的運行、磁懸浮、渦流制動、磁感應探傷以及衛星在地磁場中的運動等具有重要作用[1-5]. 在這類體系中，電磁相互作用導致的磁體與導體之間的磁懸浮力和磁阻尼力是實際應用問題的焦點.

對于相對運動的導體與磁體之間的相互作用，理論上可以用麥克斯韋方程組和洛倫茲力來解決，但除了少數高對稱性的情形外，一般很難得到解析解，所以實際應用中多采用模擬或數值計算的方法[6-7]. 另外，采用實驗方法進行研究也較為有效[8-9].

本文介紹了研究磁體與運動導體之間相互作用的實驗方法及相關的實驗裝置：位于永磁鐵下方旋轉的鋁圓柱體內，因電磁感應產生渦流，渦流產生的磁場使磁體受到力的作用，通過測量相互作用力，可以對導體內的渦流及其產生磁場的特點進行分析. 該實驗過程涉及許多電磁學的概念和定律，適合作為本科生的提高型或進階型實驗項目.

1 基本模型及測量結果

當磁體與導體之間有相對運動時，導體內的電子受洛倫茲力的作用產生運動，從而形成渦旋狀的感應電流，電流的大小和分布與導體的電導率及形狀有關，如圖1所示. 磁體產生的磁場B0向下，下方的平板導體向左運動，導體內將會產生渦旋狀的感應電流，其分布及產生的磁場BI大致如圖1所示. 值得注意的是，左半部的感應磁場與外場方向一致，總磁場加強；右半部的感應磁場與外場方向相反，總磁場減弱. 渦旋電流的大小和總磁場的大小有關，因此渦旋電流的分布在磁場區域的左右兩側是不對稱的.

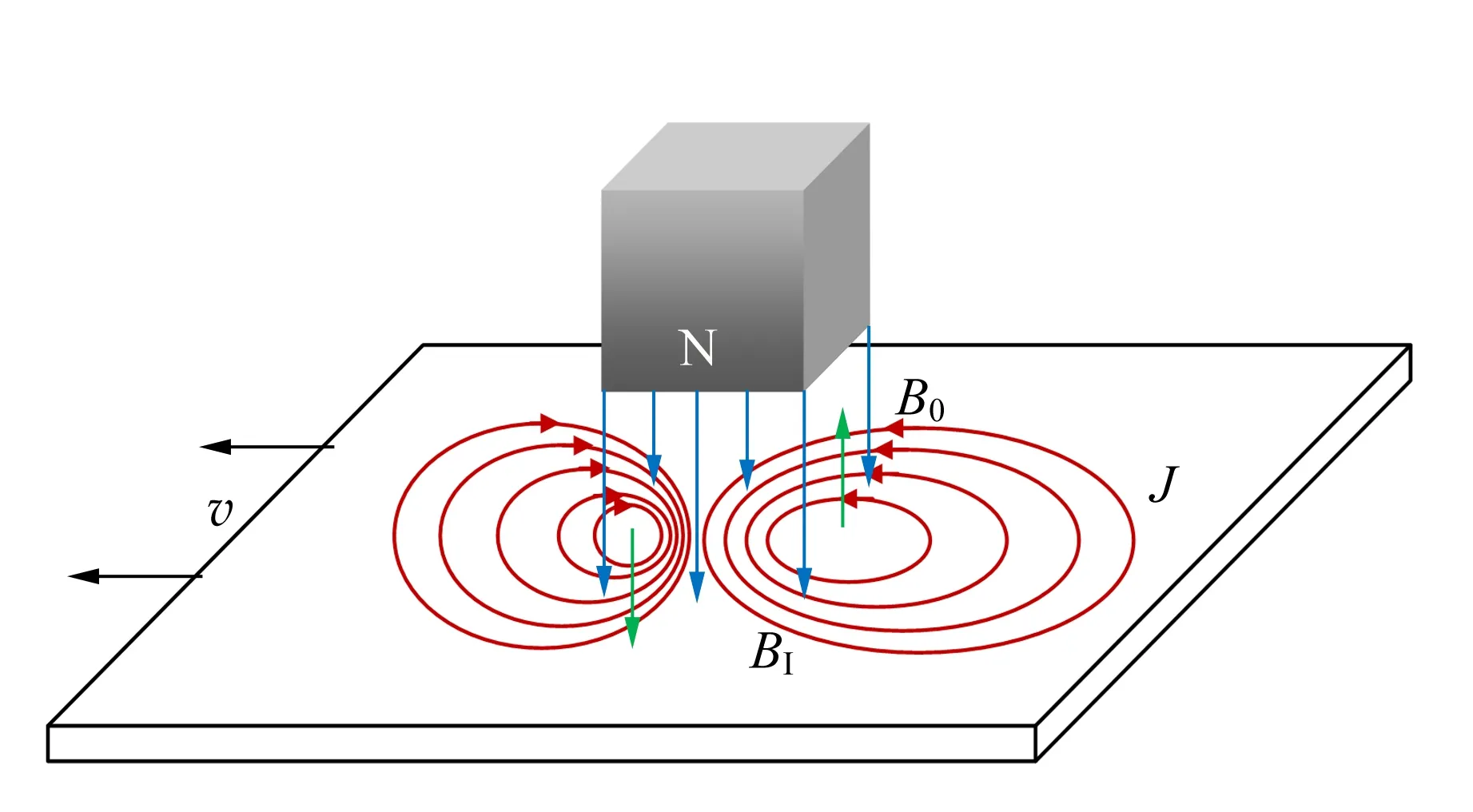
圖1 磁體與運動導體之間的電磁感應

對于不同形狀、不同運動軌跡的導體，要給出渦旋電流的分布及其與外場相互作用的解析解是很困難的，只有少數高對稱性的系統才能獲得解析解[10-11]. 所以本文用實驗方法對此進行研究，通過分析測量結果來解釋相互作用過程，并對測量結果的特征給出定性及半定量的解釋.

在實際應用中，人們最關心的是相對運動導致磁體所受水平方向的拽力(即導體所受的阻尼力)以及豎直方向的升力(磁懸浮力)，故設計了準確測量拽力和升力的實驗裝置. 由于在實驗室內較難實現導體穩定的平動，所以本文用旋轉代替平動，設計的實驗裝置如圖2所示. 位于上方的是1個安裝在特制懸臂梁上的長方形永磁鐵，可近似認為其磁感應強度在長方形區域內是均勻的，大小為B0，方向朝下；下方是繞中心軸旋轉的鋁圓柱體，旋轉角速度為ω. 旋轉的鋁圓柱體內會產生渦旋電場，渦旋電場產生感應磁場，感應磁場與原有磁場之間的相互作用導致磁體受到作用力，從而運動導體內及導體外的電場和磁場都會重新分布.

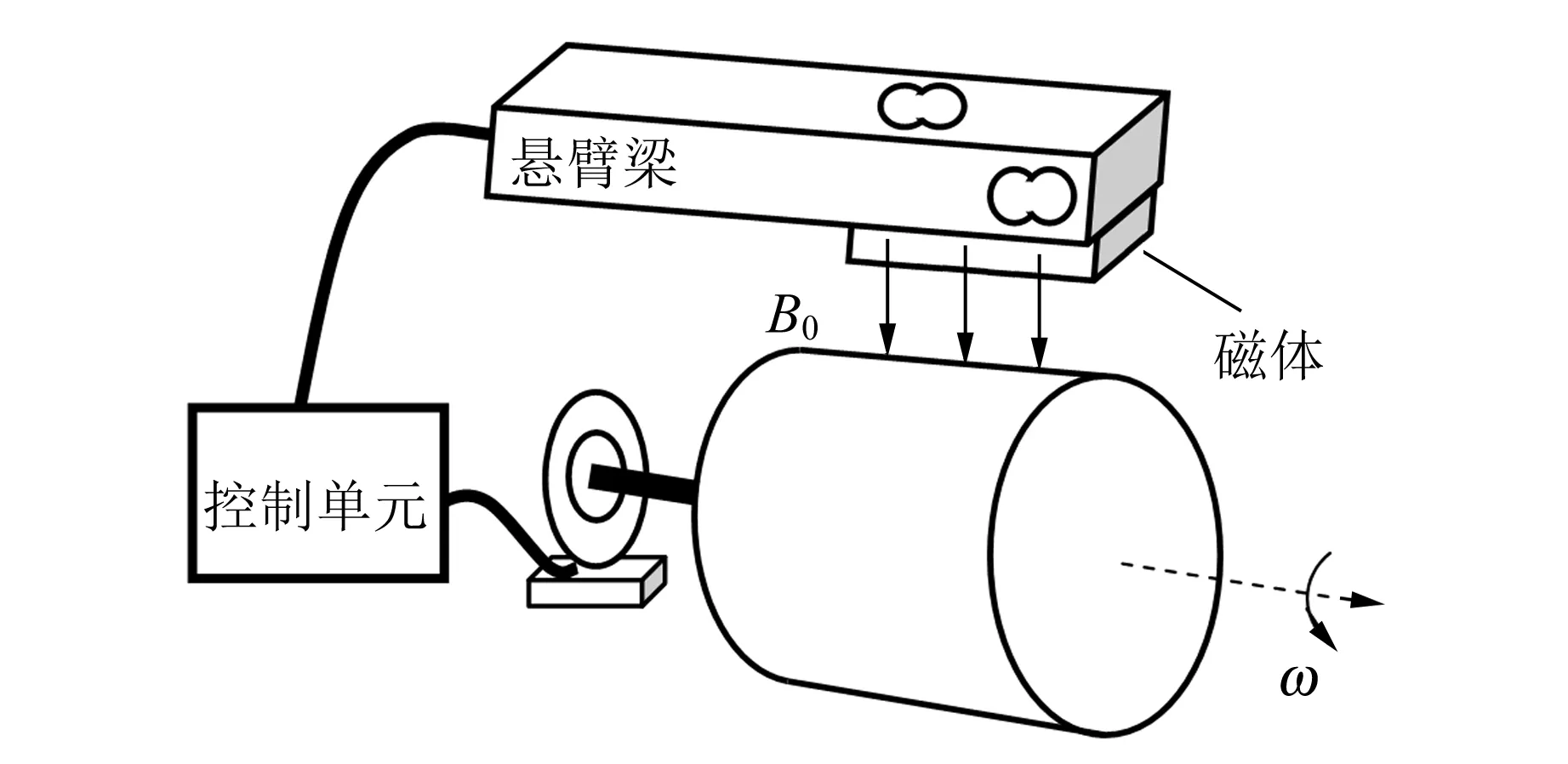
圖2 實驗裝置示意圖

利用電機驅動鋁圓柱體旋轉并控制其轉速ω，懸臂梁上安裝2個正交的力傳感器，測量磁體所受水平方向的拽力FD及磁體所受垂直方向的升力FL(磁懸浮力)，測量結果如圖3所示.從圖中可以看到，隨著轉速ω的增加，水平方向的拽力FD和垂直方向的升力FL的變化不一致.隨著轉速ω的增加，FD的增速逐漸減緩，達到一定大小后基本保持不變；FL在較大速度區間內基本上單調遞增.

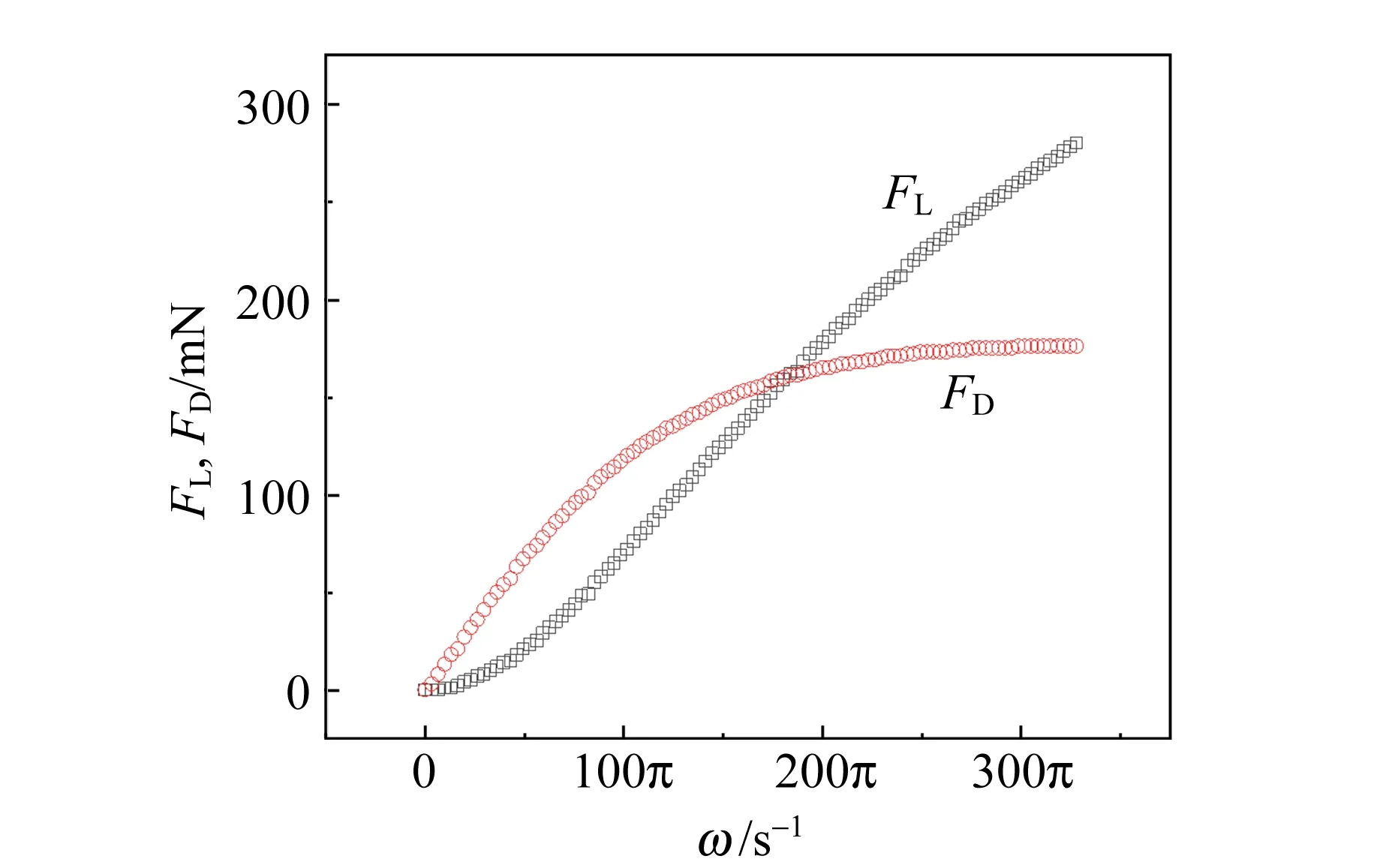
圖3 磁體所受拽力FD,升力FL與角速度ω的關系

2 對測量結果的解釋

2.1 利用迭代過程導出感應磁場的表達式

導體內的渦旋電流及其產生的磁場滿足麥克斯韋方程組：

(1)

其中最后1個方程是考慮洛倫茲力之后的歐姆定律.如果圓柱導體的旋轉速度穩定，渦旋電流及其產生的磁場與時間無關，但對于非對稱的邊界條件，從方程組較難直接求解感應電流.本文用迭代過程來取代對聯立方程組的求解：外磁場中的導體快速旋轉時，導體內將會產生渦流，而渦流又會產生磁場；此渦流產生的磁場與旋轉的導體相互作用又將產生第2個渦流，然后產生第2個磁場；第2個磁場產生第3個渦流和磁場……因此，總的磁場由無限多個場組成，因最終的結果確定存在，所以多個場的和是收斂的，或者說，該過程是負反饋過程.

基于以上過程，本文采用簡化模型來進行分析，如圖4所示.建立坐標系，假設z軸為旋轉軸，鋁圓柱體的轉動角速度為ω(逆時針方向).外場B0(假設均勻)方向指向y軸正向(實驗系統中的鉛垂方向)，感應磁場記為BI.

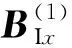
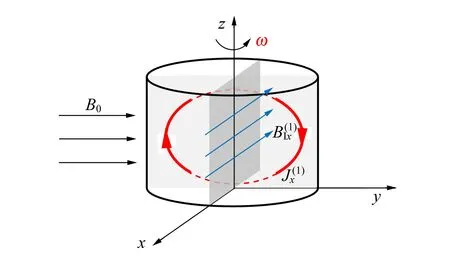
(a) 第1次迭代過程

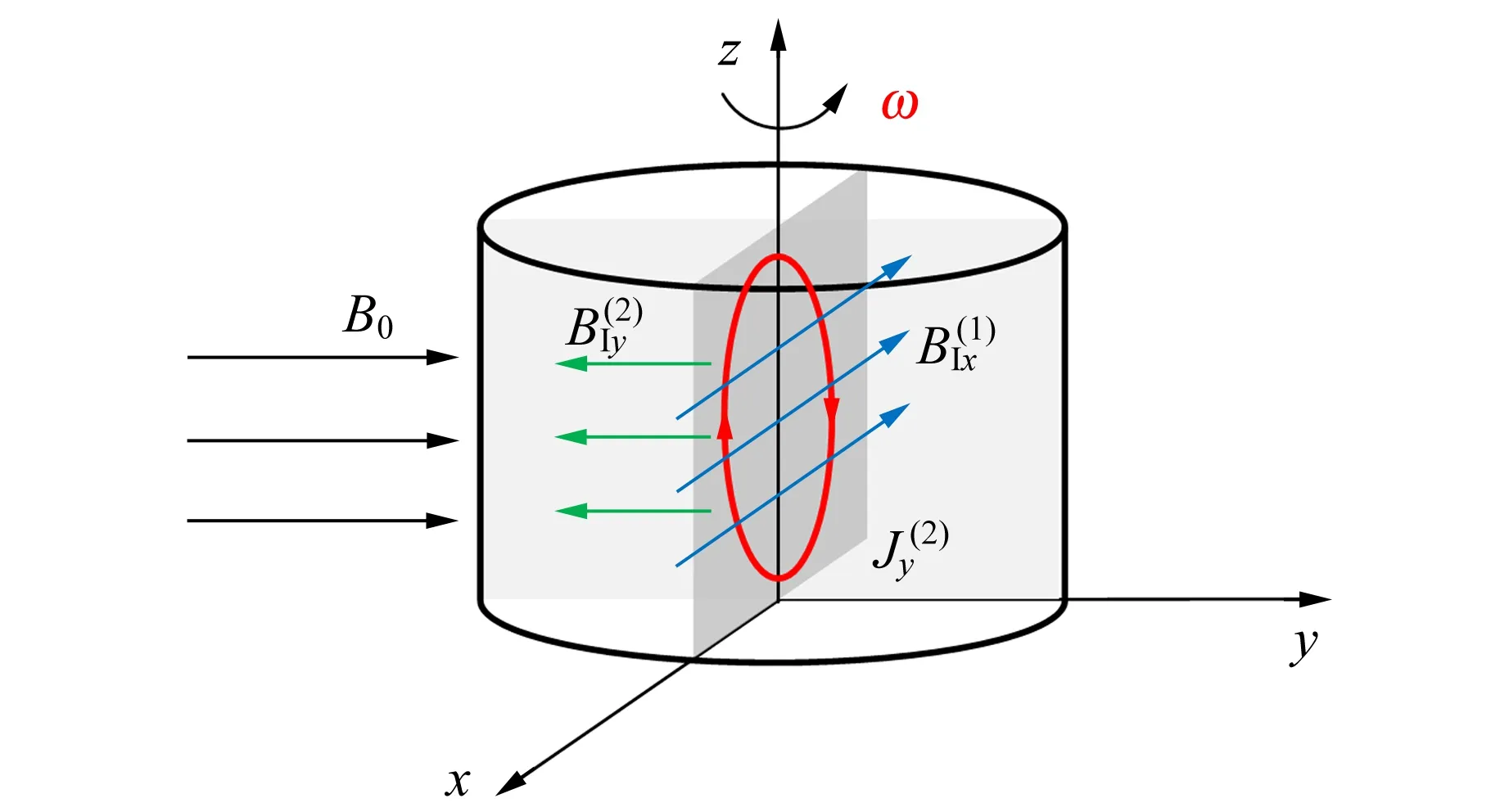
(b)第2次迭代過程圖4 利用迭代過程分析電磁感應的物理圖像

BIx=-βσωμ0rBTy=-αωBTy，

(2)

式中，負號表示BIx指向x軸的負方向，β是與導體形狀及幾何尺寸有關的常量，α=βσμ0r.

根據以上分析，同樣可得到

BIy=βσωμ0rBTx=αωBTx,

(3)

考慮到BTy=B0+BIy，BTx=BIx，再聯立式(2)和式(3)，可得感應磁場與角速度的關系為

(4)

(5)

感應磁場對永磁鐵作用力的大小與磁感應強度大小成正比，如圖4所示.磁體受到的升力(磁懸浮力)FL與y軸方向感應磁場的磁感應強度成正比(FL∝BIy)；磁體受到的拽力(阻尼力)FD與x軸方向磁場的磁感應強度成正比(FD∝BIx).

根據式(4)和式(5)，對圖3的數據進行非線性擬合，結果如圖5所示.從圖中可以看出，實驗測量結果與理論公式符合得較好，說明了理論分析合理.

圖5 磁體所受升力FL與拽力FD的實驗數據與理論值

感應磁場與角速度的關系與磁場中旋轉導體問題的理論計算及實驗結果一致[13-14]，由此推導出的FL和FD與運動速度的關系，也與磁場中的平動導體問題的理論計算及實驗結果一致[15].這說明式(4)和式(5)具有普適性.

2.2 感應磁場的特點

感應磁場BI=BIx+BIy，如圖6所示.BIx沿x軸負方向，BIy沿y軸負方向，感應磁場BI與x軸的夾角為φ.根據式(4)～(5)可知，BIy∝ωBIx，且BIy隨角速度增加的增速更快，故夾角φ隨角速度的增加也會變大，即感應磁場將隨著轉速增加而逐漸旋轉，其轉動方向與導體柱的旋轉方向一致.在極大轉速的極限情況下，BIx→0，BIy→-B0，感應磁場將會與外場大小相等、方向相反(符合楞次定律)，導體內的總磁場趨于零.當然，這種狀態不可能達到，因為隨著轉速增加,渦流的焦耳熱會越來越多，從而會限制轉速的無限增大.

為了更清楚地了解上述物理過程，本文使用霍爾片測量了靠近圓柱體表面處的磁感應強度，圖6中標出了5個磁場測量點，其磁感應強度隨轉速變化的測量結果如圖7所示.圖7中的數據為感應磁場的磁感應強度，是總場強扣除外場之后的結果(先測出外場的磁感應強度).從圖7中可以清楚地看到，隨著轉速的增加，磁感應強度的峰值點位置從1→2→3→4→5逐漸移動，說明了感應磁場在逐漸旋轉.

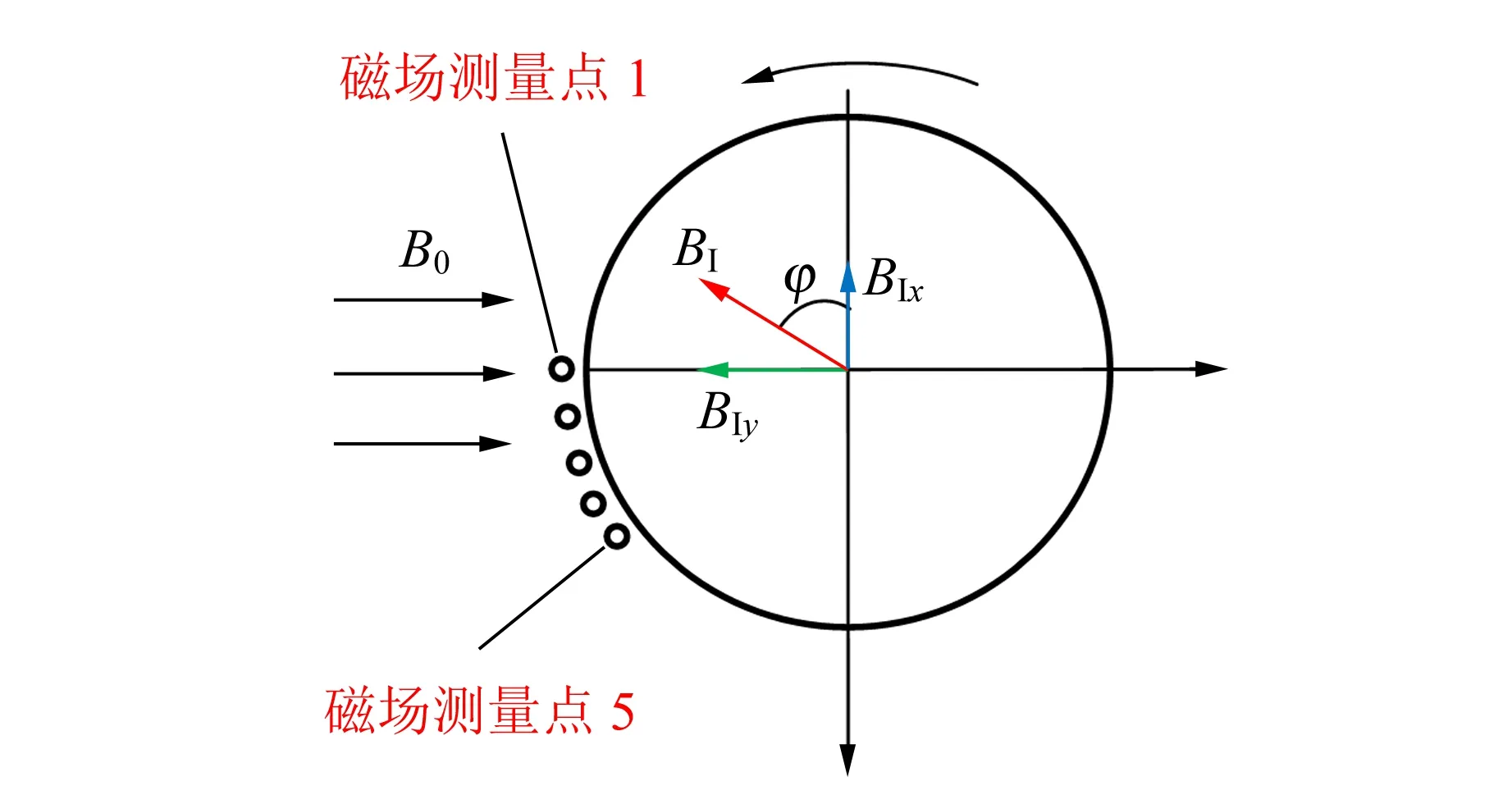
圖6 感應磁場的特點

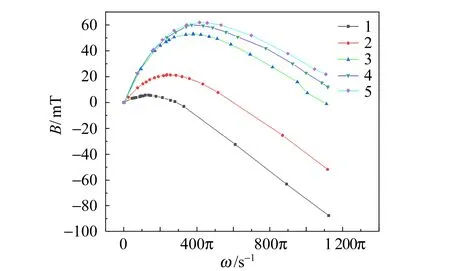
圖7 不同位置處磁場的測量結果

3 測量與分析

為進一步了解磁體的受力情況，重新設計了測力傳感器的分布.將永磁體等效看作電流恒定的矩形線圈，磁場向下時，左側電流與右側電流(紅色線條)的流向如圖8所示.在圖示位置安裝測力傳感器，可分別測量磁體左側的升力FL1和拽力FD1，同樣可測量磁體右側的升力FL2和拽力FD2.測量結果如圖9所示.很明顯，磁體左右兩側的受力情況有較大區別.特別是升力的測量結果，可以看到左側受到向上的升力，右側所受的力向下，在速度較低時，二者幾乎同步增加，所以凈升力較小，該階段的磁體實際上受到繞對稱軸(見圖8)的力矩作用.接下來，隨著速度的增加，磁體所受左側的升力增速放緩，而右側向下的力減小，所以總升力的增速基本持平.這是以前未觀察到的變化過程，該現象同樣可由上一節討論中所指出的“感應磁場的指向隨角速度增加產生旋轉”的結論進行解釋.

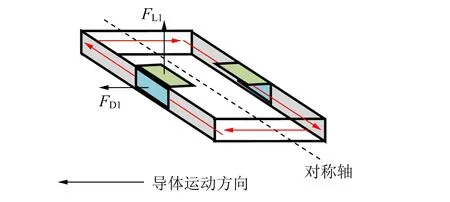
圖8 力傳感器位置示意圖

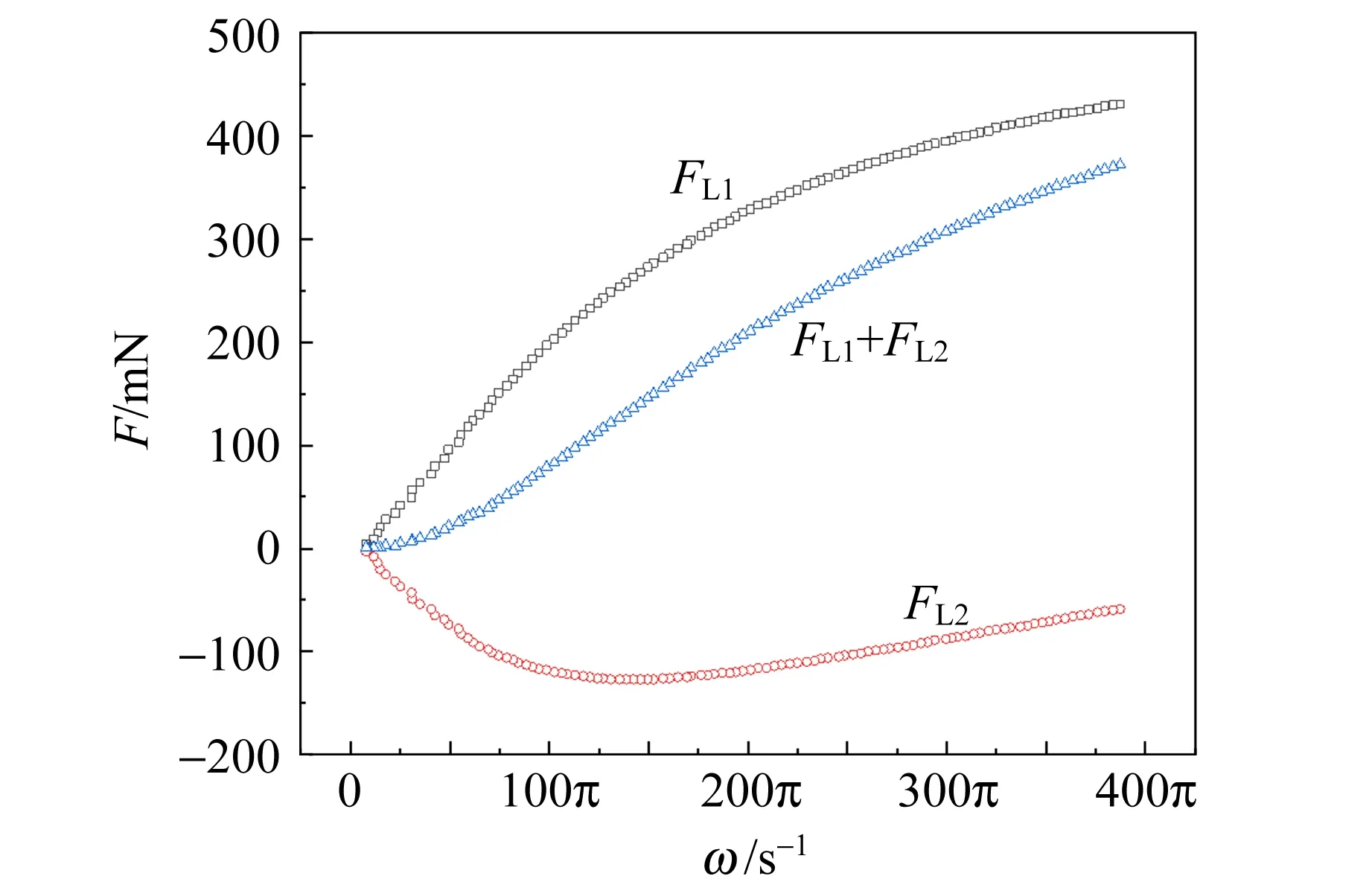
(a)升力

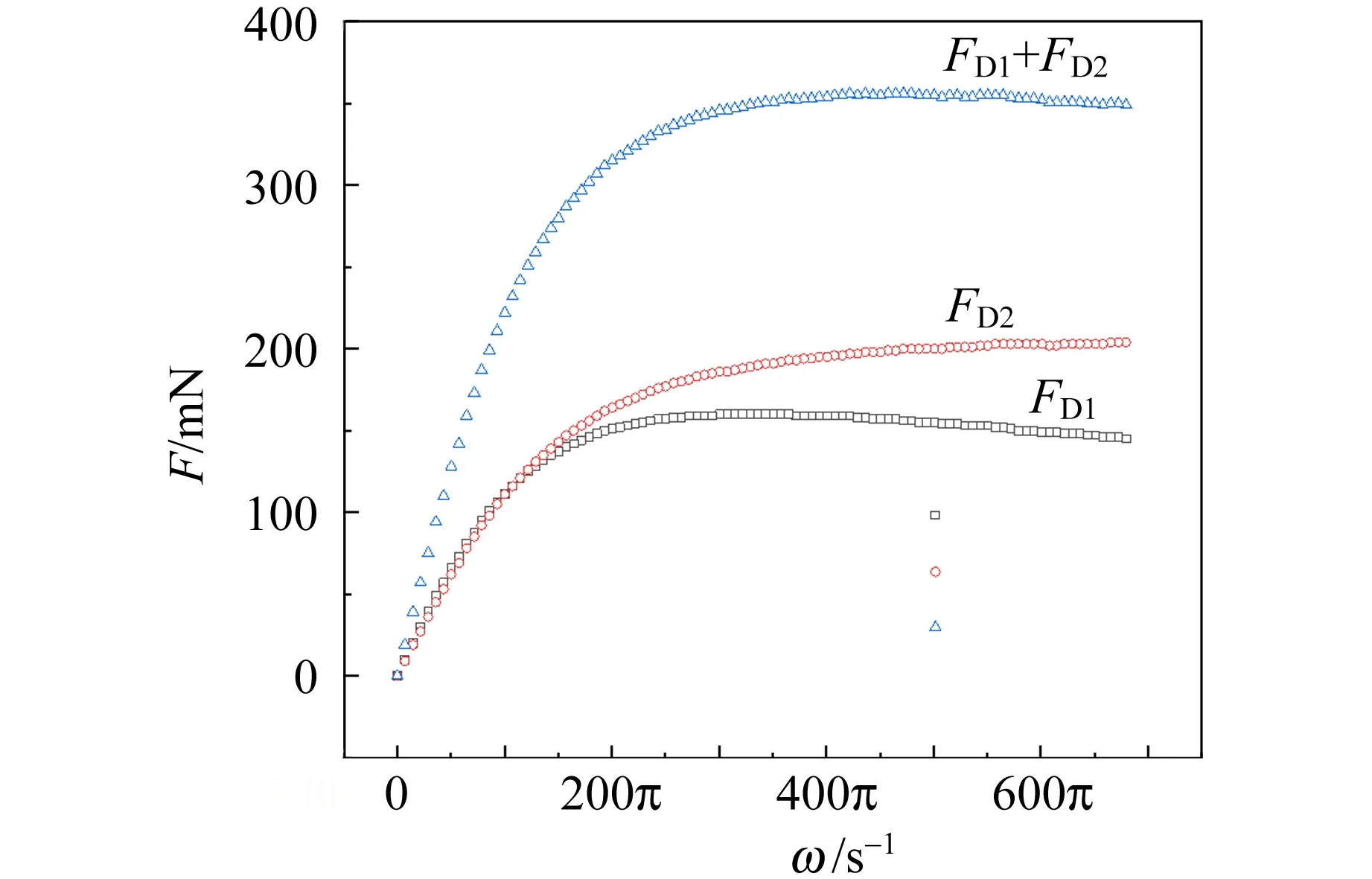
(b) 拽力圖9 永磁體左右兩側的升力和拽力

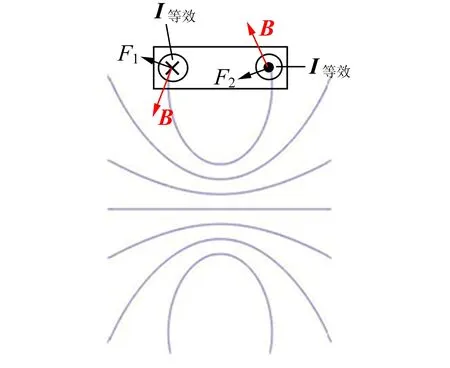
感應磁場是渦流產生的，可以用環形電流產生的磁場來大致模擬. 電流越強，磁力線越密集，感應磁場轉動，磁力線方向也會隨之轉動. 與永磁鐵等效的矩形線圈中的電流所受力的方向垂直于磁力線方向，因此可用磁力線方向的變化來解釋作用力方向的變化，如圖10所示.

1)轉速ω很小的情況，如圖10(a)所示. 此時渦旋電流很小，磁場的偏轉角φ也很小，因此可以忽略，此時磁體總的受力情況F1+F2為：水平方向受到向左的拽力(與圓柱體上表面運動方向一致)，就好像磁體被下方導體拖拽一樣；垂直方向所受的合力為0，但存在繞線圈對稱軸的力矩.

2)轉速ω稍大的情況，如圖10(b)所示.此時F1和F2都有所增加.因磁場偏轉了小角度φ，所以電流線圈處的磁力線方向也有所偏轉，故電流線圈所受的安培力也會產生一定變化：水平方向所受合力仍是向左的拽力，而且變得更大；垂直方向的合力不再為0，而是受到向上的升力——磁懸浮力，其力矩仍存在.

3)轉速ω較大的情況，如圖10(c)所示.此時磁場的偏轉角φ較大，線圈電流所受安培力的變化為：水平方向所受合力仍是向左的拽力，但力的增速變緩；垂直方向的合力(磁懸浮力)增加較快.

總之，隨著ω的增加，渦流產生的磁場的磁力線密度在增加，方向也在旋轉，導致F1和F2的大小在增加，方向也隨之旋轉.水平方向與垂直方向的合力的變化趨勢為：隨著ω的增加，水平方向的力總是向左，先是穩步增加，然后增速放緩，最后減小；垂直方向的力從0開始，逐漸出現穩步增加的升力，沒有出現減小的趨勢.

(a) ω很小

(b) ω稍大

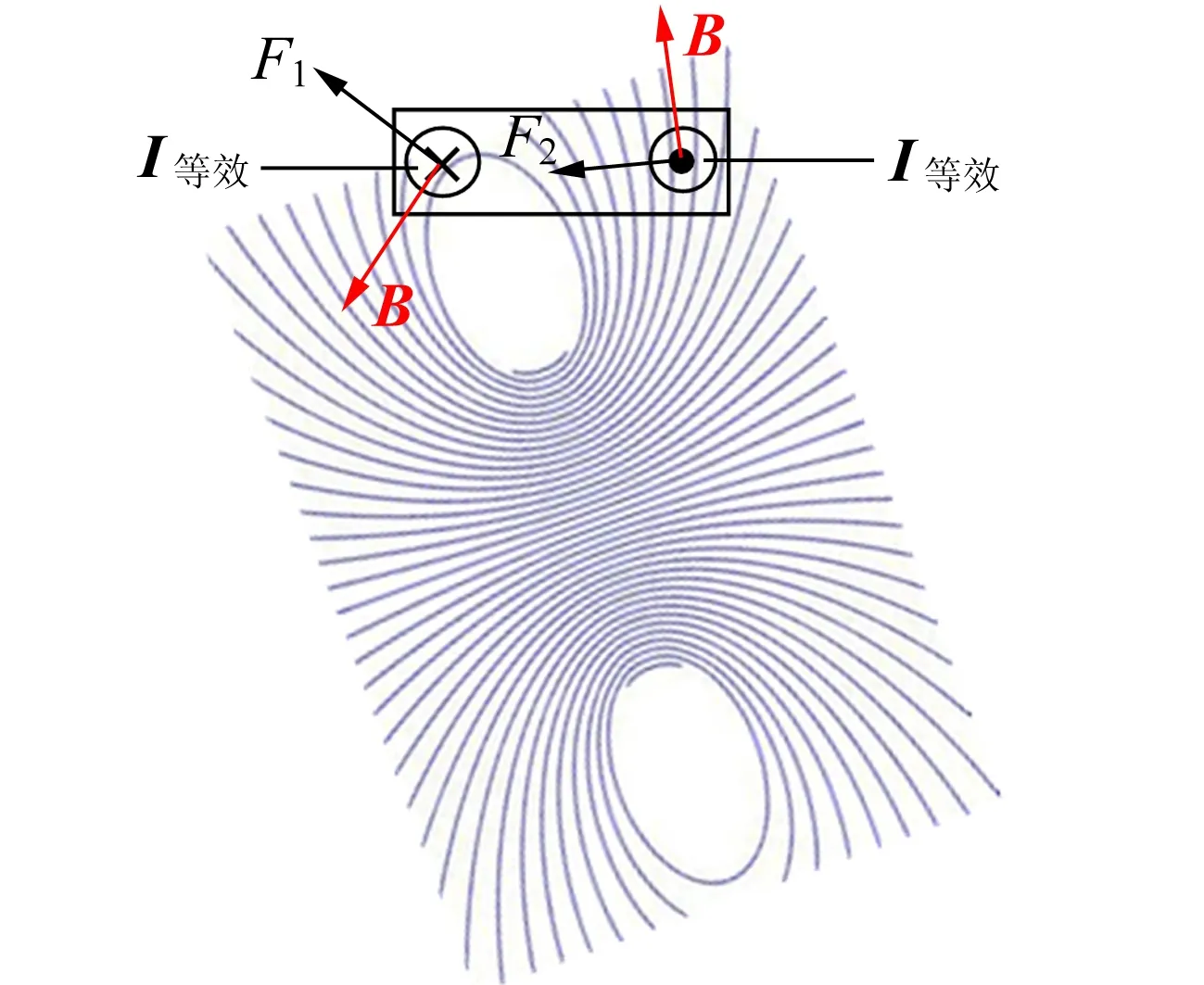
(c) ω較大

圖10 永磁體受力隨磁場轉動的變化

以上分析對應于圖9中各階段實測曲線的變化趨勢，充分說明了“感應磁場的指向隨角速度增加產生旋轉”的正確性.

4 結 論

磁體與運動導體之間的相互作用是典型的電磁相互作用，了解它們因電磁感應產生的磁懸浮力與磁阻尼力，既具有理論研究的意義，又具有實際應用價值.本文設計并制作了研究這種相互作用的實驗裝置，對磁懸浮力、磁阻尼力以及感應磁場的磁感應強度等物理量進行了測量，并利用雙梁力傳感器對磁體前后兩側的受力進行測量，觀察到了兩側作用力的變化.通過對渦流與磁場相互作用過程的分析，建立了用迭代方法描述的理論模型，得出感應磁場的方向隨角速度增加發生旋轉，并推導出了這些量與導體轉動角速度之間的關系式，這些關系式與磁懸浮力、磁阻尼力的實測數據符合得較好.根據以上結論，可以很好地解釋感應磁場的磁感應強度的測量結果，對磁體前后兩側受力的實測結果也能給出較好地解釋.本文得到的結果具有一定的普適性，對磁體與運動導體之間的相互作用系統具有參考意義.