裂縫-孔隙介質儲層滲透率表征及其影響因素分析

熊繁升， 甘利燈， 孫衛濤,2*， 楊昊

1 清華大學周培源應用數學研究中心, 北京 100084 2 清華大學航天航空學院, 北京 100084 3 中國石油集團勘探開發研究院， 北京 100083

0 引言

巖心切片電子顯微鏡實驗和數字巖心技術等最新手段研究證實，在儲層巖石內部普遍存在裂縫-孔隙形成的復雜連通網絡.在天然巖石中，流體流動發生的空間是全局性裂縫-孔隙網絡，而不是局部的單一孔隙或孔管束，因此三維裂縫-孔隙網絡模型是描述孔隙空間非均質性的一種合理方法.Fatt(1955)較早提出了孔隙介質簡化網絡模型，通過規則網絡上的管道表示孔隙空間.Bryant等(1993)提出了一個多孔介質的無序網絡模型，認為真實多孔系統孔隙尺寸隨機分布假設可能是無效的.Seeburger和Nur(1984)提出了二維孔隙空間網絡模型，用于預測砂巖的靜滲透率，砂巖和花崗巖的計算結果表明，網絡模型可以根據圍壓函數預測滲透率大小.基于流體力學基本方程.Bernabé(2009)建立了牛頓流體在剛性和彈性管網中的水力傳導率和波頻散方程.Bernabé(1995)通過管道和管網對牛頓流體的輸運特性進行了數值模擬.Johnson等(1987)得到了含流體管道中滲透率對頻率的依賴性.Blunt和King(1991)、Blunt(2001)研究了由細管形成的網絡中相對滲透率與飽和度的關系，表明網絡模型能夠解釋微觀流動如何影響厘米尺度上的平均特性.基于孔隙尺度的潤濕性變化，三維孔隙網絡也被用于模擬砂巖內部排水和注水過程(Nilsen et al., 1996; Bakke and ?ren, 1997).

大量研究表明，雖然局部非均勻孔隙/裂縫參數對孔隙流體會產生一定影響，但是在孔隙網絡節點相互連通的“均質化”效應下，其對儲層巖石整體滲透率的影響十分有限.平行排列的裂縫系統能夠較好的反映地層各向異性屬性，但是很難描述跨平行裂縫層的流體流動現象.因此，相對于研究局部孔隙-裂縫相互作用的模型來說，更需要將跨微觀-宏觀尺度的三維裂縫/孔隙網絡系統作為研究對象，從整體角度考察裂縫網絡對巖石孔隙度、滲透率、地震波頻散衰減、提高儲層采收率等諸多方面的影響.

滲透率是多孔介質的一種固有特性，它表征了多孔介質中流體流動的難易程度.達西定律描述了流體在多孔介質中的穩態流動，在這種情況下滲透率是一個靜態值.然而，天然巖石孔隙結構十分復雜，在波場作用下內部流體-固體交界面振動引起孔隙連通性改變.彎曲度是描述多孔介質中孔隙連通性和擴散路徑曲率的常用量，隨周圍壓力的變化而變化(Johnson et al., 1987; Smeulders et al., 2006).因此，振蕩流動過程中存在“動態滲透率”，換句話說，如果流體流動是由振蕩壓力引起的，滲透率將隨頻率而變化.

實驗測量發現，滲透率在低頻率下是一個恒定值，在高頻率下依賴于頻率的倒數(頻率范圍從0.1 Hz到1 kHz)(Charlaix et al., 1988)，一般認為隨著頻率增大，存在著從黏性流態到慣性流態的過渡，實驗觀測也提供了黏彈性流體滲透率增強的證據(Mena et al., 1979; Castrejón-Pita et al., 2003).Johnson等(1987)進行了動態滲透率模型的研究，采用分支函數法推導了隨機孔隙中與波的耗散相關的動態滲透率一般表達式，并通過設計不同實驗證實這個模型可以很好描述高低頻極限下彈性波的響應規律，在中間頻率能給出較合理的近似.Blanc等(2013)從流體固體的本構關系和動量守恒方程式出發，將動態滲透率結合到二維孔隙介質波動方程中，修正了耗散項，通過算子轉化實現在時間域進行求解.Müller等(2007)研究了隨機分布孔隙空間中的動態滲透率變化規律，并推導此類分布下動態滲透率的數學表達式.Chapman等(2002)提出了從微觀尺度建立孔隙彈性介質模型的方法，該模型假設孔隙網絡節點與臨近其他節點之間的流體流動滿足達西定律，利用達西定律導出宏觀流動-壓力方程，但是該模型并沒有給出宏觀裂縫系統滲透率表達公式，滲透率作為一個計算參數，需要通過實驗手段測量得到.Xiong和Sun(2020) 分析了任意三維孔隙網絡中流體流變學特征和孔隙連通關系對巖石滲透率的影響，發現滲透率變化受脈沖壓力波場頻率、流體流變學屬性和孔隙連通性的影響.

在含有裂縫/軟孔隙的儲層巖石中，流體流動路徑往往受到孔隙截面閉合的影響而發生改變.但是，目前關于裂縫-孔隙網絡的研究多集中于圓形截面的管道網絡，這種網絡空間可以用來表征硬孔隙對滲透率的影響，但無法解釋在壓力作用下軟孔隙壓縮甚至閉合帶來的影響.利用橢圓截面微管網絡模擬儲層巖石流體流動空間的工作尚不多見，主要原因在于圓形截面的孔隙管道流體流動問題相對簡單，易于給出簡潔的表達式；而橢圓截面孔隙管道的流場速度數學建模復雜，很難用簡單函數得到解析表達式.

基于巖石內部的裂縫連通網絡特征，本文提出了具有橢圓截面的裂縫/軟孔隙三維網絡模型(圖1).該模型通過在橢圓坐標系下為單個橢圓截面裂縫/軟孔隙管道流場速度建模，利用無量綱流量與縱橫比無關的條件，將橢圓坐標系下馬蒂厄函數轉換為圓柱坐標系下貝塞爾函數，獲得裂縫/軟孔隙流量解析表達式，并利裂縫/軟孔隙網絡節點流通量守恒條件，得到振蕩壓力作用下儲層巖石的整體滲透率計算方法.

1 三維橢圓截面微管網絡模型

在三維橢圓截面微管網絡模型中，引入了裂縫體密度、裂縫縱橫比和裂縫長度、孔隙度等參數，并在宏觀滲透率與微觀參數之間建立了聯系，研究發現這些參數對于孔隙介質整體滲透率具有重要影響.

給定邊長為l的巖石樣本單元立方體，沿X、Y、Z方向上分別排布有M、N、L個橢圓截面微管(圖1).在X-Y平面內，分布有M×N個裂縫，并沿Z方向排布有(L-1)個間隔，因此沿Z方向上共有M×N×(L-1)個微裂縫.同理，在Y方向上分布有M×L×(N-1)個微裂縫，在X方向上分布有N×L×(M-1)個微裂縫.單元體內的裂縫數密度定義為：

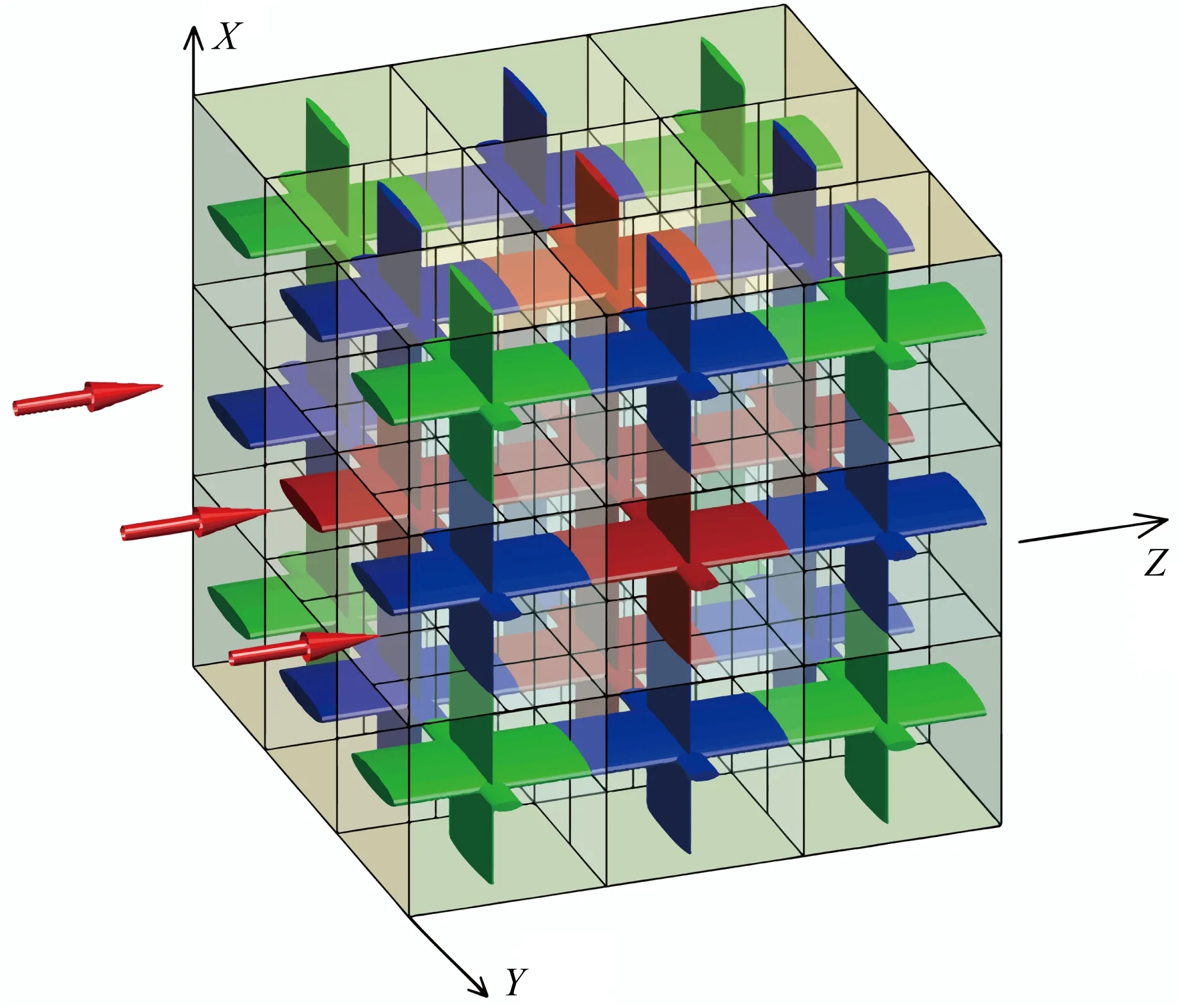
圖1 由橢圓截面毛細管構成的三維裂縫網絡模型Fig.1 Schematic diagram of 3D fracture network model composed of capillary tubes with elliptic cross section

(1)

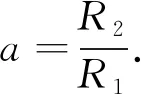
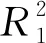
(2)

繼而得到孔隙度為：

(3)

在后續計算中，常常需要給定裂縫網絡體密度、孔隙度，以便考察滲透率隨裂縫縱橫比的變化情況.因此，這里給出已知裂縫體密度參數M、N、L和孔隙度φ，求解裂縫主半徑長度的公式：

(4)

其中，巖石樣本邊長l可以取做實驗特征長度，或者取做滲透率預測所需要尺度.在給定孔隙度情況下，當裂縫的縱橫比很小，裂縫的寬度可能非常大，甚至超過了巖石樣本的邊長l，此時把裂縫的寬度限制在一定范圍內，例如在X方向上，裂縫最大寬度小于l/(M-1).這種情況下，裂縫網絡的孔隙度可能會小于預設值.因此，在縱橫比取非常小的數值時，單個裂縫/軟孔隙的空間受到限制，模型孔隙度存在一個上限.該模型具有以下特點：

(1)單個管道橫截面是縱橫比可變的橢圓形，可以模擬從狹窄裂縫/軟孔隙到圓形硬孔隙的不同類型裂縫-孔隙網絡空間；

(2)在微觀尺度上單個微管(半徑處于微米量級)相互連接，形成宏觀網絡(整體單元處于厘米～米量級)，實現孔隙介質中跨尺度整體建模，能夠更好的反映孔隙系統整體效應；

(3)將裂縫/軟孔隙近似成橢圓微管網絡，可以簡化物理建模和數學推導，得到精度很高的解析解，同時又不失對裂縫/軟孔隙整體空間的特征刻畫；

(4)裂縫/軟孔隙網絡模型的滲透率依賴于壓力振蕩頻率，因此可以應用于不同頻率下滲透率變化情況.

當然，裂縫網絡是一種等效孔隙介質模型，其中包含的裂縫寬度、長度等參數與巖石切片中觀察到的實際尺寸并非一一對應，而是對真實儲層巖石中裂縫/孔隙理想化建模的等效參數.等效參數與實驗觀測數值之間存在不一致，甚至是相差很大，但是對于等效巖石物理模型來說，這些參數數值是合適的，能夠從整體上實現對儲層巖石滲透率的預測.通過對來自不同文獻的多種類型砂巖實驗數據對比表明，三維裂縫/軟孔隙網絡模型確實可以定量預測出多種巖樣滲透率分布范圍，并估計出對應巖石孔隙縱橫比.

2 橢圓截面微管中流體速度場和流量

首先采用橢圓柱坐標系，給出含不可壓縮牛頓流體在橢圓截面微管中的流量表達式(圖2).

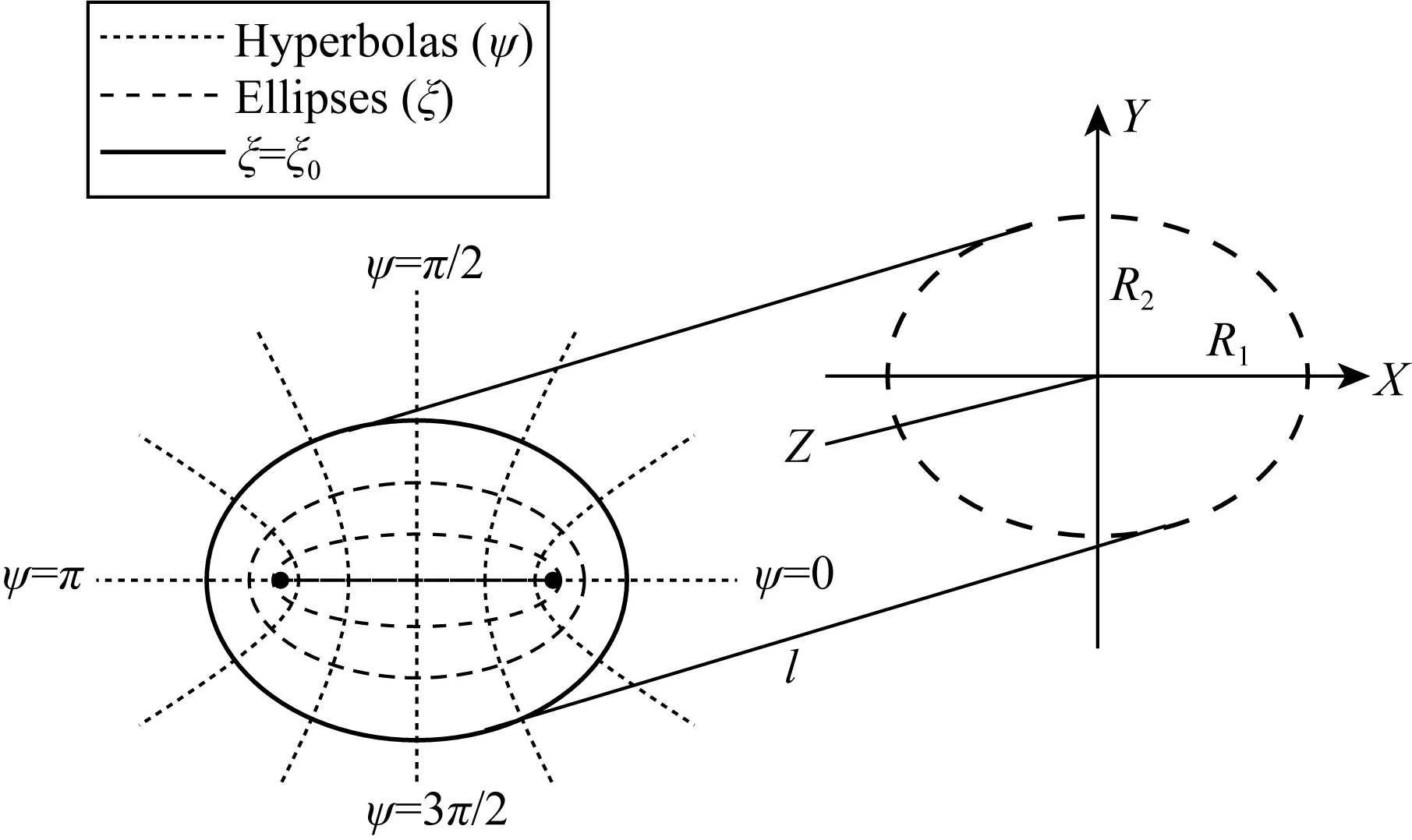
圖2 橢圓柱坐標系下橢圓截面微管模型Fig.2 Microtubule model with elliptic section in elliptic cylindrical coordinate system

橢圓柱坐標徑向、軸向坐標分別以ξ、ψ和z表示，根據微管道對稱性條件，流體質點軸向速度可以表示為u=u(r,z,t)，徑向速度表示為v=v(r,z,t)，流體壓力表示為p=p(r,z,t)，壓力振蕩頻率為ω，微管中流體的密度、粘度分別為ρf、η.

基于長波長假設，壓力梯度沿微管道軸向分布，徑向速度分量為零(Maslen,1958).微管中的流體在壓力作用下發生流動，并使壓力在微管流體中發生傳播.孔隙流體流速很低，因此流體壓縮性可以忽略.考慮到流體速度非零分量沿z軸(軸向)方向，其大小隨徑向坐標而變化，流體滿足方程：

(5)

其中ρf是流體密度，p是流體壓力.設橢圓截面兩個焦點之間的距離是2d，ψ=ψ0表示一族共焦點雙曲線，ξ=ξ0表示一族共焦點橢圓，這里ξ0和ψ0是常數.利用坐標變換關系式：

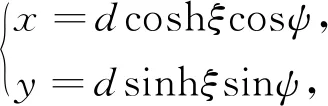
(6)

得到橢圓柱坐標系下的Navier-Stokes方程：

(7)

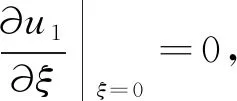
u(ξ,ψ,z,t)=U(ξ,ψ)e-iω(t-z/c)，

(8)

p(ξ,ψ,z,t)=P(ξ,ψ)e-iω(t-z/c)，

(9)

代入Navier-Stokes方程得到：

(10)

式(10)是關于U的非齊次微分方程, 這里c是流體中聲波的速度(復數).

當裂縫/孔隙壓力隨時間和空間變化時，流體的速度場是時間和空間的函數，可以表示為穩態場和非穩態場的疊加：

u(x,y,t)=u0(x,y,z)+u1(x,y,z,t)，

(11)

代入Navier-Stokes方程并利用邊界條件和分離變量方法，得到穩態速度場的空間分布(Haslam, 1997)：

u0(ξ,ψ)=

(12)

通過在橢圓微管截面上積分，容易得到穩態流量表達式：

(13)

將速度寫為壓力P(ξ,ψ)的函數，代入Navier-Stokes方程得到非穩態解(Haslam, 1997)：

(14)

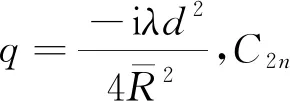
(15)

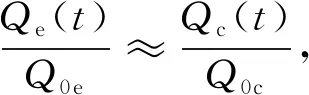
(16)

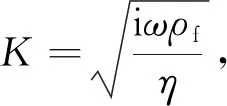
(17)

這里Qc(t)是圓形截面微管的流量.因此可以通過圓形截面微管流量和縱橫比來計算橢圓形截面微管流量.

3 裂縫/軟孔隙流體流量與壓力振動頻率關系

Bernabé(Bernabé, 2009)研究了諧波振蕩壓力下圓柱形管道的流體流動問題，給出了流體流量與頻率、流體密度、粘性、管道半徑和長度等參數之間的關系式.本文將該方法推廣到了具有橢圓形截面的微管流量計算中.下面考慮橢圓裂縫微管長度為L0，管兩端壓力分別為PU、PD，流量分別為QU、QD，此時管內壓力為沿相反方向傳播的兩種壓力波的疊加：

p(z,t)=B+e-iω(t-z/c)+B-e-iω(t+z/c)，

(18)

管內總流量表示為

q(z,t)=Q+e-iω(t-z/c)+Q-e-iω(t+z/c).

(19)

利用邊界條件p(0,0)=PU和p(L0,0)=PD，得到：

(20)

利用初始邊界條件和無量綱流量關系式，得到壓力波作用下橢圓截面微管流量表達式：

(21)

其中：

(22)

結合達西定律得到橢圓柱體通道的流體傳導系數：

(23)

其中A=aπR2為截面面積，R是橢圓截面長軸半徑.因此，流量與壓力之間滿足：

Qe=k(PU-PD)，

(24)

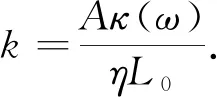
4 裂縫/軟孔隙流體流量與圍壓的關系

對于橢圓截面的裂縫，當裂縫截面縱橫比a較大時，截面接近正圓，孔隙結構抵抗外部圍壓的能力較強，不易變形；當裂縫截面縱橫比a很小時，裂縫截面兩側邊緣互相接近，抵抗外部圍壓的能力較弱，容易發生較大變形，影響流體的流動特征.因此，當a較小時，在孔隙/裂縫滲透率計算中需要引入孔隙/裂縫的彈性形變理論.

考慮截面積相對較小的裂縫，其長度方向延伸較長，因此可以將裂縫的彈性形變看作平面應變問題.在含裂縫巖石中，當裂縫十分狹窄時，裂縫兩個邊緣十分接近，裂縫尖端呈楔形.設裂縫截面的長軸和短軸半徑分別為R1、R2，Mavko和Nur(1978)研究了楔形尖端裂縫在圍壓作用下的變形問題，并給出了裂縫長度和寬度方向半徑隨圍壓的變化關系.當孔隙介質外部受到外部圍壓pc作用時，半徑形變與壓力pc之間滿足：

(25)

(26)

其中ν、E是固體骨架礦物材料的泊松比和楊氏模量.因此，裂縫截面縱橫比可以表示為圍壓的函數：

(27)

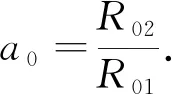
將半徑-壓力關系式代入速度場流量表達式，得到裂縫流量隨圍壓的變化關系式為

(28)

其中:

(29)

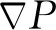
5 含三維裂縫/軟孔隙網絡多孔介質滲透率計算

上面得到了單裂縫流量隨縱橫比、壓力變化頻率、巖石圍壓等參數變化關系式，為了建立由微裂縫組成的三維裂縫/軟孔隙網絡孔隙介質滲透率，首先采用流量計算公式得到每個微管的流道，然后利用微管兩端每個節點的流量守恒條件(克希霍夫定律)，得到全部網絡節點滿足的流量-壓力線性方程組.該方程組未知量為各節點的壓力，入口和出口端的壓力邊界條件是方程非齊次項.求解該方程組得到各節點壓力后，計算巖石樣本整體三維網絡流量，進而根據壓力邊界條件和流量得到巖石樣本滲透率.網絡節點上流量守恒滿足：

(30)

這里Z為與節點i相連接的其他節點總數目.記N為網格的節點個數，Γ為節點連接矩陣，Γ∈RN×N，Γ的元素僅由0和1組成，Γ矩陣元素的賦值規定為：若節點i和節點j相連γij=1，否則γij=0；對任意節點i均有γii=0，即節點與其本身不相連；矩陣Γ是對稱的.

考慮連接網絡節點i和j的任意一段微管，節點處的壓力分別為pi和pj，微管流量是pi和pj的函數，采用線性關系可以表示為

Qij=cijpi+dijpj，

(31)

這里系數cij和dij是與所選這兩個節點之間微管參數(管長、半徑)相關的參數，采用式(31)作為壓力差與流量的關系式，則有cij=ij，dij=δij，其中：

(32)

(33)

(34)

這里Lij與Rij分別表示節點i與j所連接微管的長度與主半徑，aij是截面縱橫比，這里有cij=cos(ωLij/c0)·dij，c0=1/(βρ)是聲波在流體中的傳播速度，β為流體壓縮系數，ω是脈沖壓力波場頻率.

對各節點列流量平衡方程式，得到以下形式方程組：

(35)

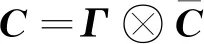
將系數矩陣分裂為兩個矩陣相加，A=M+N，其中對角陣M表示為

(36)

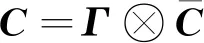
6 數值算例

6.1 砂巖滲透率預測與實驗數據對比

為驗證所建立的三維裂縫/軟孔隙多孔介質滲透率模型可靠性，選取4類巖樣實驗數據進行對比分析：致密氣砂巖，固結砂巖，非固結砂巖，新沉積海灘砂.巖樣滲透率隨孔隙度變化的實驗數據來自于PetroWiki(2015).

在本算例中，三維裂縫/軟孔隙模型計算參數為：空間三個方向上網絡維度為M=5,N=5,L=5，模型巖樣邊長1 cm, 孔隙度范圍為φ=0～55%, 縱橫比范圍為a=0.001～1.砂巖礦物材料密度為2650 kg·m-3，體積模量為37 GPa，剪切模量為44 GPa，砂巖泊松比采用0.2.孔隙流體為水，其密度為1000 kg·m-3，體積模量為2.15 Gpa，黏性為0.001 Pa·s.

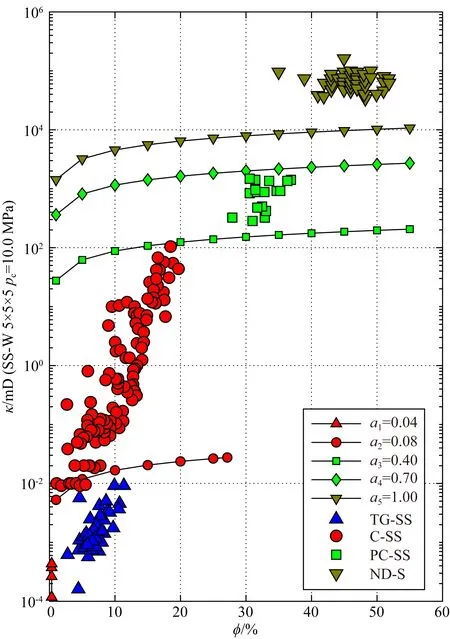
圖3 含水砂巖滲透率-孔隙度交會圖 采用新沉積的海灘砂和來自油氣田測井的三套樣品(Petrowiki, 2015)，TG-SS: 致密氣砂巖；C-SS:固結砂巖；PC-SS: 弱固結砂巖； ND-S: 新沉積海灘砂.Fig.3 Permeability-porosity cross plot of water-bearing sandstone Using newly deposited beach sand and three sets of samples from oil and gas field logging (Petrowiki, 2015).TG-SS: Tight gas sandstone; C-SS: Consolidated sandstone; PC-SS: Weakly consolidated sandstone; ND-S: Newly deposited beach sand.

這里計算了在圍壓為10 MPa件下含水砂巖滲透率-孔隙度交會圖(圖3)，孔隙流體承受的振蕩壓力頻率為20 Hz.圖3給出了不同縱橫比下得到的含三維裂縫/軟孔隙網絡砂巖滲透率-孔隙度關系曲線.計算結果顯示，理論模型預測的滲透率-孔隙度變化范圍與實驗數據吻合很好(新沉積海灘砂除外).隨著縱橫比從0.04增加到1，滲透率從10-4mD增加至105mD(1 mD=0.987×10-3μm2)，對于同一個縱橫比，滲透率隨著孔隙度增加而增大，但是增加趨勢逐漸平緩.

在數據圖中，致密氣砂巖滲透率范圍較低(10-4～10-2mD).模型預測結果顯示，實驗數據點分布在縱橫比分別為0.04和0.08的界限之間(圖3).這個結果表明，真實致密氣砂巖中的裂縫/孔隙對滲透率的影響，可以用三維裂縫網絡模型中縱橫比為0.04和0.08的等效裂縫/孔隙網絡表示.

在準確預測出滲透率范圍的同時，理論模型預測的裂縫/軟孔隙縱橫比能否與真實巖石中縱橫比吻合，這是人們關心的重要問題.Smith等(2009)在研究低孔低滲致密氣砂巖的速度-孔隙度關系時發現，微裂縫對致密氣砂巖的P波速度起到至關重要的作用，需要引入較大的縱橫比分布范圍才能解釋所有的觀測數據點.他們的結果顯示(Smith et al., 2009)，致密氣砂巖的實驗數據點分布在以縱橫比0.05為中心的一個變化范圍內，這與本文模型預測的縱橫比分布范圍(0.04～0.08)一致，從多個文獻中不同數據和分析方法的相互印證可以看出，三維裂縫網絡模型對致密氣砂巖滲透率和孔隙縱橫比的預測是可信的.

固結砂巖滲透率實驗數據分布的范圍較為寬泛，覆蓋了從0.01 mD到100 mD的范圍(圖3).Burns等(1990)研究了利用直接觀測和速度反演手段獲得固結砂巖孔隙縱橫比的方法，對Navajo、Weber和Kayenta砂巖樣本的實驗數據分析顯示，砂巖孔隙的縱橫比均大于0.01，其中含有黏土的固結砂巖孔隙縱橫比主要分布在以0.2為均值的范圍內.這個結果與本文對固結砂巖的預測范圍(0.08～0.4)十分吻合(圖3)，可以看出理論模型預測的縱橫比數值再一次得到了實驗數據的驗證.

弱固結砂巖的滲透率實驗數據分布在約100 mD到1000 mD之間(圖3).Alam等 (2014a,b)通過實驗手段測量了不同溫度和圍壓下經過短時間(24 h)固結的Shikotsu熔結凝灰巖和Kimachi砂巖孔隙縱橫比，與地下儲層巖石億萬年的長期固結作用相比，短時間固結的樣本是一種弱固結砂巖.他們的測量結果顯示(Alam et al., 2014a,b)，在1 MPa圍壓作用和353 K溫度下，巖石孔隙縱橫比主要分布在0.2至0.85之間，其中以0.45至0.65占優；在15 MPa圍壓作用和295 K溫度下，縱橫比主要分布在0.3至0.8之間，其中以0.4至0.6占用.本文模型對弱固結砂巖縱橫比的預測范圍是0.4至0.7(圖3)，這與Alam等學者對弱固結砂巖的實驗結果吻合的很好.

新沉積海灘砂的滲透率實驗數據分布在約50～100 D之間(圖3)，由于砂粒完全沒有固結，顆粒之間的孔隙空間松散，本文滲透率模型預測的結果低于實驗測量值.

6.2 裂縫/軟孔隙體密度對巖石滲透率的影響

巖石中裂縫/軟孔隙的連通程度對于滲透率有重要影響.當裂縫體密度增加時，裂縫之間的間距降低，彼此連通度變得更加緊密；當體密度降低時，裂縫之間的間距增加，裂縫變得更加稀疏，相互之間的連通關系降低.Lucia(1983)研究發現，碳酸鹽滲透率與裂縫寬度三次方成正比，與裂縫間距成反比.我們分別計算了裂縫網絡規模從4×4×4、5×5×5到6×6×6不斷增加的情況，其對應裂縫體密度分別為144、300和540.為了對比分析裂縫密度、縱橫比的影響，我們還對不同孔隙度、不同縱橫比下的網絡進行了計算(圖4，圖5).

由圖4可以看出，恒定孔隙度條件下，滲透率隨裂縫/軟孔隙密度增加而增大.我們發現，當裂縫/軟孔隙網絡規模從4×4×4加密到5×5×5時，滲透率曲線約上升17%左右；當裂縫/軟孔隙網絡規模從5×5×5加密到6×6×6時，滲透率曲線約上升25%左右.因此可以看出，隨著裂縫/軟孔隙密度的增加，裂縫之間的連通程度提高，巖石滲透率逐步增大；反之，當裂縫之間連通程度降低時，滲透率下降.相比于Lucia(1983)對碳酸鹽的研究工作，本文的理論建模過程從不同角度出發得到了一致的結論；同時，Davudov和Moghanloo(2018)對頁巖滲透率隨孔隙可壓縮性和連通性變化規律的研究發現，隨著等效壓力的增加，裂縫/孔隙連接數量逐漸下降，滲透率隨著逐漸降低.這些工作從多個方面研究了滲透率-裂縫體密度之間的關系，通過對比前人工作發現，三維裂縫/軟孔隙網絡模型符合已有研究得到的規律，并且能夠實現滲透率隨裂縫參數變化規律的定量預測計算.

從圖4、圖5中可以看出，滲透率隨著縱橫比的增加而顯著增大(跨越近8個數量級)；我們發現，隨著縱橫比接近1，這種增大趨勢逐漸降低.同時，在給定縱橫比情況下，滲透率隨著孔隙度增加而增大，這種增加趨勢并非線性，而是逐漸趨于緩和.

在圖4a中，由于縱橫比很小(0.04)，其裂縫網絡存在一個孔隙度上限，因此孔隙度范圍的最大值只有約15%左右；當縱橫比上增加到0.08時，裂縫網絡對應的孔隙度上限也有所增大，達到約30%左右(圖4b).當裂縫縱橫比繼續增大時，孔隙度可以達到預設范圍最大值55%左右(圖5).

7 結論

基于橢圓截面微管道在振蕩壓力作用下的流體速度場和流量建模，提出了含三維裂縫/軟孔隙網絡多孔介質滲透率計算方法，得到了含多孔介質宏觀滲透率與孔隙度、縱橫比、裂縫/軟孔隙體密度等參數之間的關系.數值計算結果表明，相同孔隙度下縱橫比對滲透率有顯著影響，滲透率的數值可以跨越幾個數量級；相同縱橫比條件下，滲透率隨著孔隙度增加而增大，同時，這種增長趨勢依賴于孔隙度數值，低孔隙度下增長趨勢更明顯.相同孔隙度下，滲透率隨著網絡密度的增加而增大，而且在更高的裂縫/軟孔隙體密度下，滲透率的增強效應更明顯.理論模型數值計算與實驗數據對比分析表明，三維裂縫/軟孔隙網絡模型得到的認識與現有實驗結果吻合很好，更重要的是該模型提供了一種根據裂縫幾何特征、壓力、頻率、巖性等實驗可測量參數定量計算儲層巖石宏觀滲透率的方法，計算結果考慮到了裂縫/軟孔隙的大范圍連通效應，相比局部孔隙、管道建模方法更具真實性.

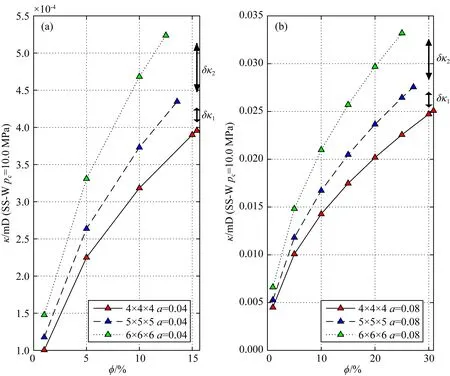
圖4 滲透率隨孔隙度、裂縫/軟孔隙密度曲線 (a) 縱橫比為0.04； (b) 縱橫比為0.08.其中δκ1為裂縫網絡規模從4×4×4加密到5×5×5時引起的滲透率變化， δκ2為裂縫網絡規模從5×5×5加密到6×6×6時引起的滲透率變化.Fig.4 Permeability curves as function of porosity, fracture/soft pore density (a) Aspect ratio of 0.04; (b) Aspect ratio is 0.08.δκ1 is the permeability change caused by the size of the fracture network from 4×4×4 to 5×5×5, and δκ2 is the permeability change caused by the size of the fracture network from 5×5×5 to 6×6×6.

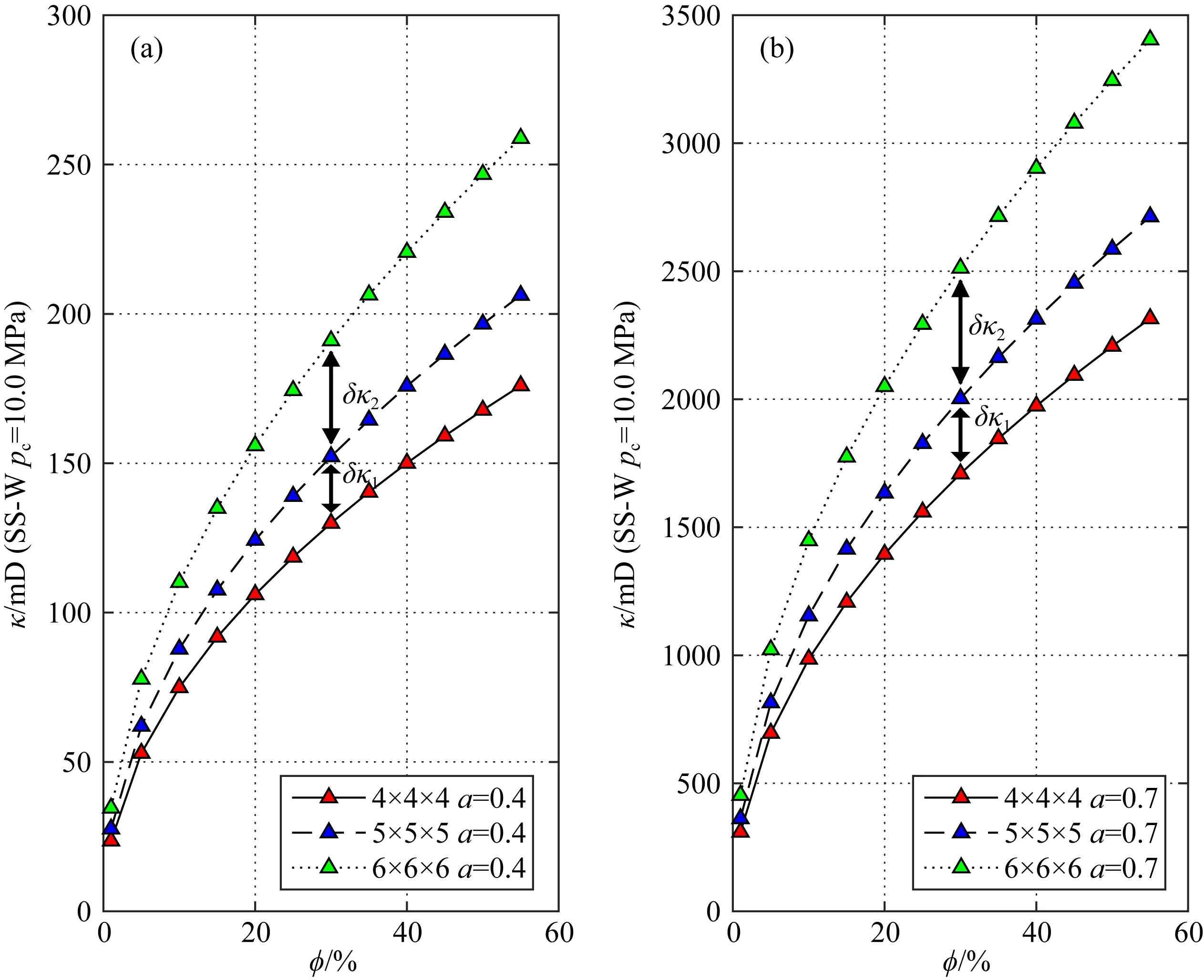
圖5 滲透率隨孔隙度、裂縫/軟孔隙體密度曲線 (a) 縱橫比為0.4； (b) 縱橫比為0.7. 其中δκ1為裂縫網絡規模從4×4×4加密到5×5×5時引起的滲透率變化， δκ2為裂縫網絡規模從5×5×5加密到6×6×6時引起的滲透率變化.Fig.5 Permeability curves as function of porosity, fracture/soft pore body density (a) Aspect ratio of 0.4; (b) Aspect ratio is 0.7. δκ1 is the permeability change caused by the size of the fracture network from 4×4×4 to 5×5×5, and δκ2 is the permeability change caused by the size of the fracture network from 5×5×5 to 6×6×6.