基于多目標FCS-MPC的永磁同步發電機MTPA控制

邱建琪，吳翊銘，史涔溦

(浙江大學 電氣工程學院，浙江 杭州 310027)

永磁同步發電機PMSG由于結構簡單、效率高及可靠性高等優點，在現代工業中被廣泛使用。由于PMSG輸出交流電壓，其幅值和頻率隨著轉速變化而變化，因此在PMSG的輸出端需要通過整流器將交流電壓變換成穩定的直流電壓，從而保持輸出電壓的穩定。常用的整流方式有二極管不控整流和脈沖寬度調制(pulse width modulation，PWM)整流2類。

目前對于永磁同步發電機PWM整流的常用控制策略是電壓外環和電流內環的雙閉環PI矢量控制，根據d，q軸電流分配策略，又可以分為id=0控制、最大轉矩電流比MTPA控制和弱磁控制等。但在實際PI控制中，控制效果對系統參數的依賴度很高，且不同工況下最優PI參數不同，因此在變工況控制情況下控制效果欠佳[1-4]。

近年來，有限集模型預測控制FCS-MPC由于其結構簡單、多目標控制及良好的非線性控制效果等特點被廣泛應用在永磁同步電機控制領域中。FCS-MPC根據系統模型，預測有限集合中每個控制組合作用下在未來周期中被控變量的變化，通過代價函數計算得到最優控制組合，實現被控變量對參考變量的跟蹤。該算法響應迅速、魯棒性強，能夠有效克服PI控制中參數整定復雜、受環境影響等缺點。目前,已有大量文獻開展了針對永磁同步電動機PMSM的FCS-MPC控制的研究，然而在發電系統中，目前對于PMSG穩壓控制的預測控制研究較少，故PMSM的預測控制策略對基于PWM整流器的PMSG穩壓控制具有較大研究意義[5-7]。

對于永磁同步發電機的id=0控制，可以采用基于電流模型預測的方法實現，即通過給定d，q軸電流計算電流代價函數從而得到最優電壓矢量[8]。在中低速工況下，對于永磁同步凸極發電機系統，通過MTPA控制策略，可以最大限度提高效率，在保證有效輸出同時降低相電流，有利于開關器件工作。為了實現MTPA，需要先計算得到某個轉矩參考下的d，q軸電流參考值，然后基于矢量控制或者電流模型預測控制來實現后續的電壓矢量分配[9]。課題組針對上述方法，提出了一種基于多目標FCS-MPC的永磁同步發電機MTPA控制方法，在FCS-MPC基礎上，通過多目標優化實現轉矩參考值跟蹤及MTPA優化控制，可以代替傳統的基于雙閉環PI的矢量控制及電流模型預測控制，具有較強的魯棒性和良好的動靜態性能。

1 PMSG穩壓系統

永磁同步發電機穩壓系統的拓撲如圖1所示，包括PMSG、PWM整流器、電容及直流負載。原動機拖動電機轉動，輸出三相交流電壓，通過PWM整流器和電容轉換成穩定的直流電壓，供給負載。

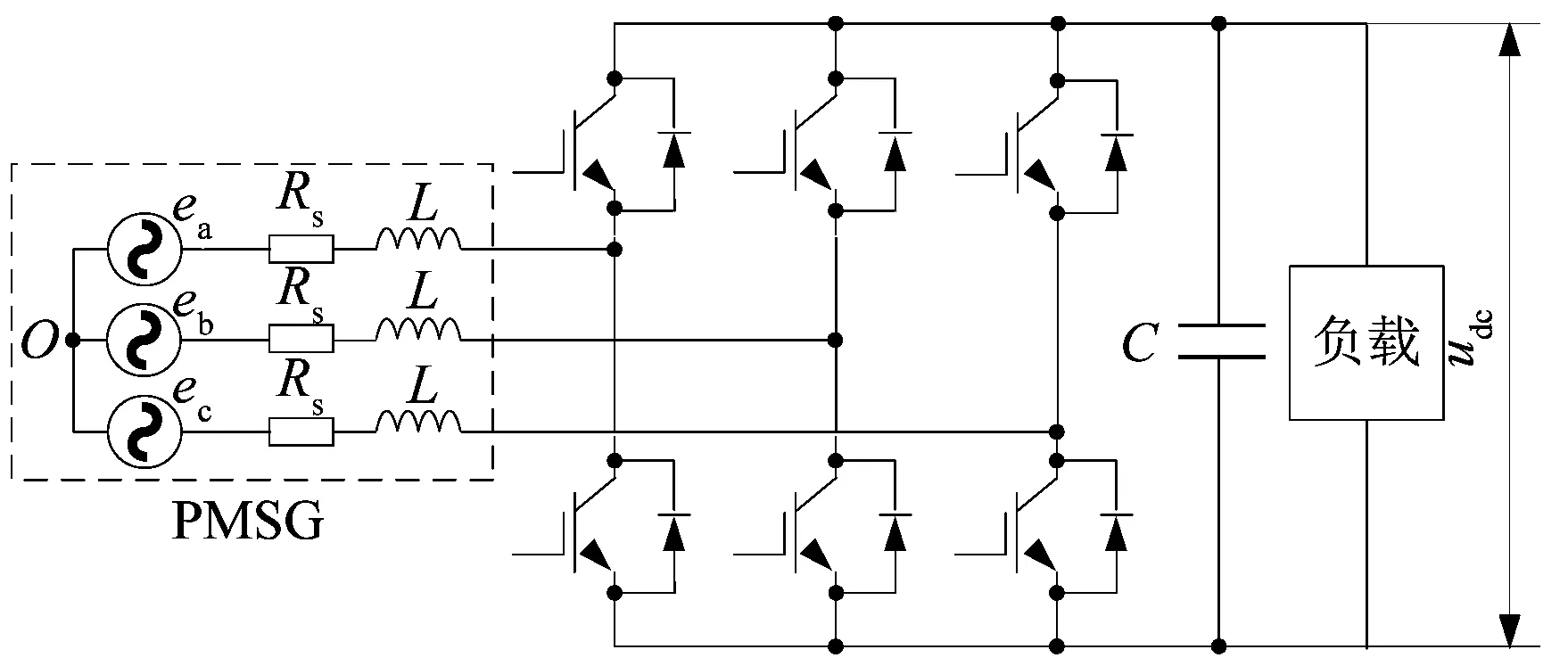
圖1 PMSG系統拓撲Figure 1 Topology of PMSG system

在電動機慣例下，PMSG在同步旋轉坐標系中的模型如下：

(1)

電磁轉矩方程為：

Te=1.5pn[ψfiq+(Ld-Lq)idiq]。

(2)

式中：ud，uq為定子d，q軸電壓；id，iq分別為定子勵磁電流、轉矩電流；Rs為定子電阻；Ld，Lq為電機d，q軸電感；ω為電機的電角速度；ψf為永磁體磁鏈；pn為電機極對數;Te為電機的電磁轉矩。

當控制周期足夠小時，可以認為模型的各個變量在控制周期中保持不變，采用歐拉算法可對式(1)進行離散化，離散公式如下：

(3)

式中Ts為采樣周期。

將式(3)代入式(1)，可得PMSG的離散數學模型為：

(4)

式中：k為當前采樣周期，k+1為下一采樣周期；ud(k)，uq(k)分別為當前周期定子電壓d，q軸分量；id(k)，iq(k)分別為當前周期定子電流d，q軸分量；id(k+1)，iq(k+1)分別為下一周期定子電流d，q軸分量。

2 控制優化目標

2.1 轉矩控制

轉矩預測的模型可由式(2)得出：

Te(k+1)=1.5pn[ψfiq(k+1)+(Ld-Lq)id(k+1)iq(k+1)]。

(5)

式中Te(k+1)為下一周期的轉矩預測值。

(6)

在系統的每個周期中，保證電磁轉矩的代價函數最小，能夠有效地實現轉矩跟蹤。

2.2 MTPA控制的實現

為了提高PMSG穩壓系統的控制效率，當原動機運行在中低速工況下，期望通過最小的定子電流產生最大的電磁轉矩滿足負載的需求，即對PWM整流器采用最大轉矩電流比MTPA控制。

設定子電流矢量is與d軸呈θ角度關系，則電流在d,q坐標系下的電流分量分別為：

(7)

式中is為定子電流幅值。

將式(7)代入式(2)得：

(8)

以定子電流幅值不變為條件，為了實現電機的最大電磁轉矩輸出，需要得到最優的夾角θ，即求取式(8)以θ為變量的極值點，應滿足：

(9)

聯立式(7)和式(9)可得：

(10)

由式(10)可得到永磁同步發電機MTPA控制時的運行軌跡，如圖2所示[10]。

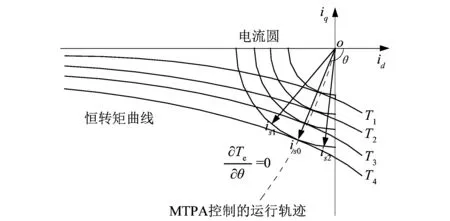
圖2 永磁同步發電機MTPA控制的運行軌跡Figure 2 Track of PMSG MTPA control

如圖2所示，永磁同步發電機的恒轉矩曲線集中在第3象限，MTPA的運行點為電流極限圓與恒轉矩曲線的切點，各切點構成了MTPA的運行軌跡。

課題組將MTPA控制與永磁同步發電機的FCS-MPC算法結合，通過增加一個目標優化項，實現PMSG的MTPA預測控制。建立MTPA的代價函數如下：

(11)

由式(10)和式(11)可知，為了實現MTPA控制，使工作點位于MTPA軌跡上，應控制代價函數fMTPA盡可能接近0。

2.3 最大電流約束

為了保證開關器件和永磁同步發電機系統的安全，需要約束允許通過的最大電流，令最大電流為imax,具體方式為在代價函數中引入一個限流輔助項如下：

(12)

當電機的定子電流幅值小于等于imax時，系統并無過流，此時限流代價函數為0；當定子電流幅值大于imax時，系統存在過流危險，此時代價函數產生作用，限流保護開啟，通過多目標代價函數的作用，控制系統電流小于限幅值。

3 多目標優化實現

3.1 多目標優化代價函數

由上文可知，為了實現永磁同步發電機PMSG穩壓系統的MTPA控制，控制方法中包含多個優化目標，為了實現多目標優化，設計系統的代價函數為：

f=KTefTe+KMTPAfMTPA+Kimaxfimax。

(13)

式中：KTe，KMTPA，Kimax為對應代價函數的權值系數，通過調試權值系數可以得到最優的多目標優化效果，并且在變工況后也無需調節系數。

在系統的動態過程中，轉矩誤差較大，此時電磁轉矩代價函數起主導作用，實現轉矩的快速跟蹤。在系統的穩態過程中，轉矩跟蹤基本實現，MTPA優化代價函數起主導作用，系統將根據此刻的負載工況進行電流的調節，確保PMSG穩壓系統始終保持在MTPA運行軌跡上。電流約束代價函數則一直約束定子電流在安全范圍內，用于保護開關器件和電機的安全，避免因過流造成系統損壞[11]。

3.2 矢量集約束

在FCS-MPC控制算法中，對于三相PWM整流器，由于每相橋臂有2種開關狀態，所以矢量集一共包括8種電壓矢量，8種電壓矢量對應的開關狀態如圖3所示。

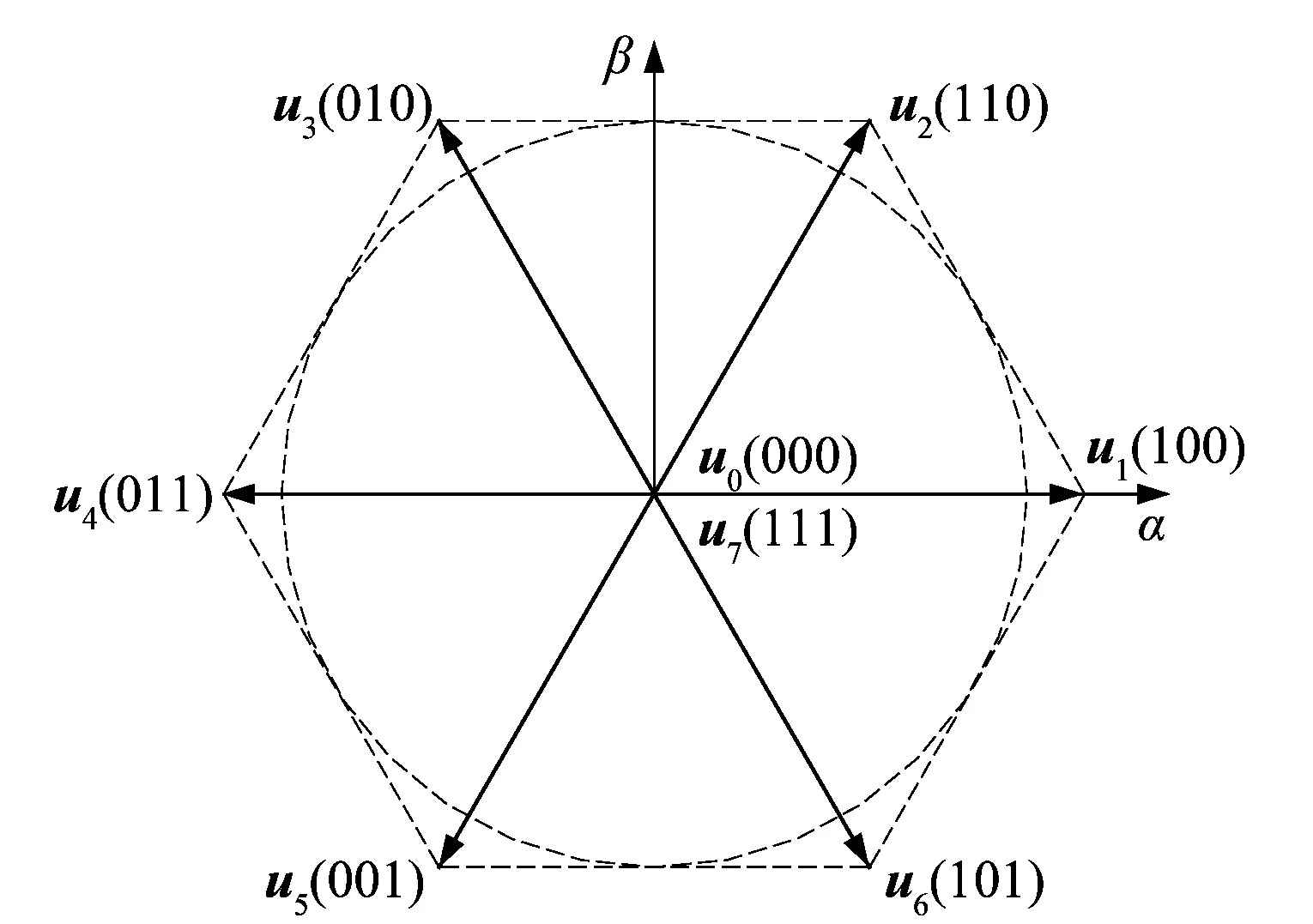
圖3 三相PWM整流器的8種電壓矢量Figure 3 Eight voltage vectors of three-phase PWM rectifier

傳統的基于電流模型預測的id=0控制框圖如圖4所示，由當前電流值預測下一時刻的電流值，電壓外環輸出iq給定值，計算電流代價函數fid和fiq，通過計算不同電壓矢量作用下的電流代價函數，得到最優電壓矢量，并轉換成開關信號作用于PWM整流器。

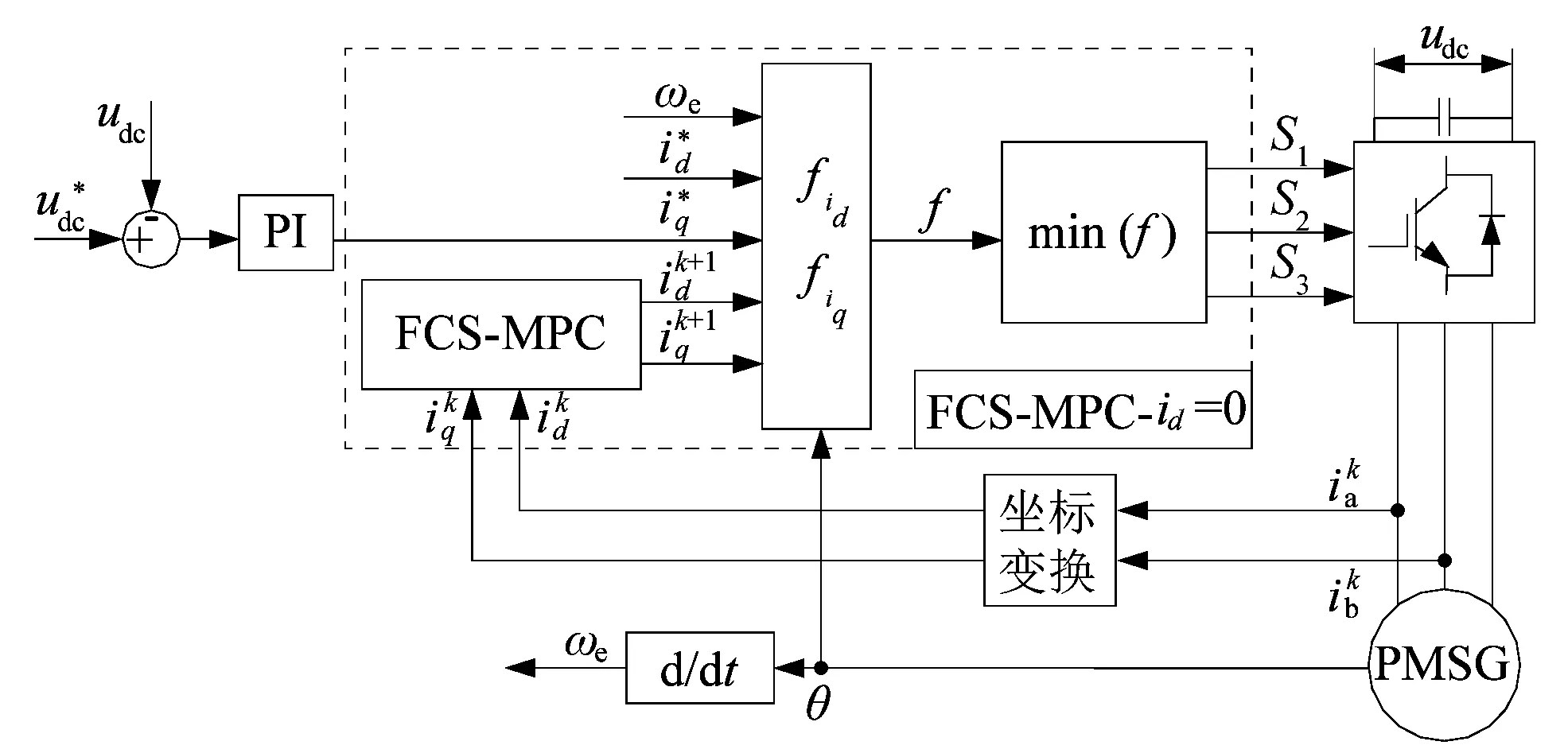
圖4 基于電流模型預測控制的PMSG的id=0控制框圖Figure 4 Control block diagram of PMSG id=0 control based on current model predictive control

圖5所示為本文控制方法的框圖，由當前時刻電流值預測下一時刻的電流值和轉矩值，電壓外環輸出轉矩參考值后，分別計算不同電壓矢量作用下的多目標優化代價函數，并選取使代價函數最小的電壓矢量，通過PWM整流器開關器件實現系統的控制。

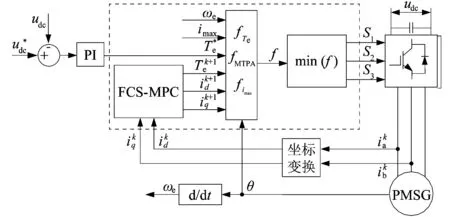
圖5 基于FCS-MPC的PMSG的MTPA控制框圖Figure 5 Control block diagram of PMSG MTPA control based on FCS-MPC

4 仿真分析

為了驗證課題組所提控制方法的正確性與可行性，在MATLAB/Simulink平臺上對PMSG穩壓系統進行了仿真。系統參數如表1所示。

表1 PMSG參數Table 1 Parameters of PMSG

課題組對永磁同步發電機穩壓系統，分別進行基于電流模型預測的id=0控制仿真，及基于多目標FCS-MPC的MTPA控制仿真，并進行對比。

仿真系統的主要參數如下：給定母線電壓參考值為100 V，相電流限幅為5 A，穩態工況時原動機轉速為350 r/min，負載為100 Ω。為了驗證系統的動態性能，進行了卸載和加速的仿真。穩態和動態的波形如圖6所示。

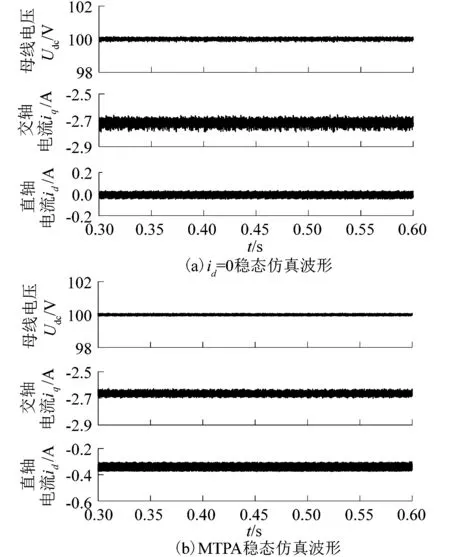
圖6 PMSG基于電流模型預測的id=0控制和基于多目標FCS-MPC的MTPA控制的仿真波形Figure 6 Simulation waveforms of PMSG id=0 control based on current model prediction and MTPA control based on multi-objective FCS-MPC

圖6所示的仿真中，卸載仿真即在穩態運行時，將100 Ω負載突卸至空載，加速仿真即在穩態運行時，將350 r/min的原動機轉速突增至500 r/min。

由圖6(a)和(b)可知：當系統處于穩態時,直流電壓均穩定在給定值，采用文中提出的多目標FCS-MPC方法進行控制時，為了提高運行效率，MTPA優化目標項控制勵磁電流id=-0.34 A,由id，iq可得定子電流幅值ia=2.69 A，小于id=0控制時的2.75 A，有效優化了系統效率，實現了永磁同步發電機整流系統的MTPA控制。

由圖6(c)和(d)可知：在0.45 s時刻系統突卸負載后，通過文中提出方法進行控制，約0.04 s后系統穩定運行在新的工況，id穩定在0 A，且直流電壓的跟蹤效果較為良好。隨著負載的改變，勵磁電流id可以實現有效自適應調節。

由圖6(e)和(f)可知：在0.45 s時刻原動機突增轉速后，通過多目標FCS-MPC方法，經過0.03 s的動態變化，電壓仍穩定在給定值，id變為-0.13 A，定子電流幅值仍小于id=0控制時的幅值，實現了系統的MTPA控制。由圖可知，由于此時轉速較高，MTPA控制的電流穩定性優于id=0控制。

仿真結果表明：采用多目標FCS-MPC方法進行MTPA控制，系統運行狀況穩定，動態響應平滑，隨著負載和轉速的變化，勵磁電流id可以實現自適應調節，使整個運行過程中系統始終能運行在MTPA軌跡上，有效實現了永磁同步發電機系統的MTPA控制。

5 實驗驗證

對上述仿真分析進行實驗驗證。實驗所用硬件平臺如圖7所示。圖7(b)中，測功機起原動機作用的。

圖7 系統硬件平臺Figure 7 System hardware platform

在Keil軟件中分別編寫id=0電流預測控制和多目標FCS-MPC的MTPA控制程序。由于實際實驗中，計算與采樣都不能實時完成，不能忽略，故實驗中對系統延時進行了補償，即通過計算下一個采樣周期的代價函數來進行滾動優化。

實驗中設置開關頻率為16 kHz，PWM整流器輸出外接100 Ω電阻，給定直流母線電壓為100 V，穩態實驗轉速為350 r/min。在實驗中，由于硬件平臺非理想情況，無法做到絕對空載，且開關器件對開關頻率有限制，與仿真相比存在誤差電流。

穩態實驗波形如圖8(a)和(b)所示。穩態運行時系統突卸負載至空載，得實驗波形如圖8(c)和(d)所示。在穩態運行時，突增轉速至500 r/min，記錄實驗波形如圖8(e)和(f)所示。

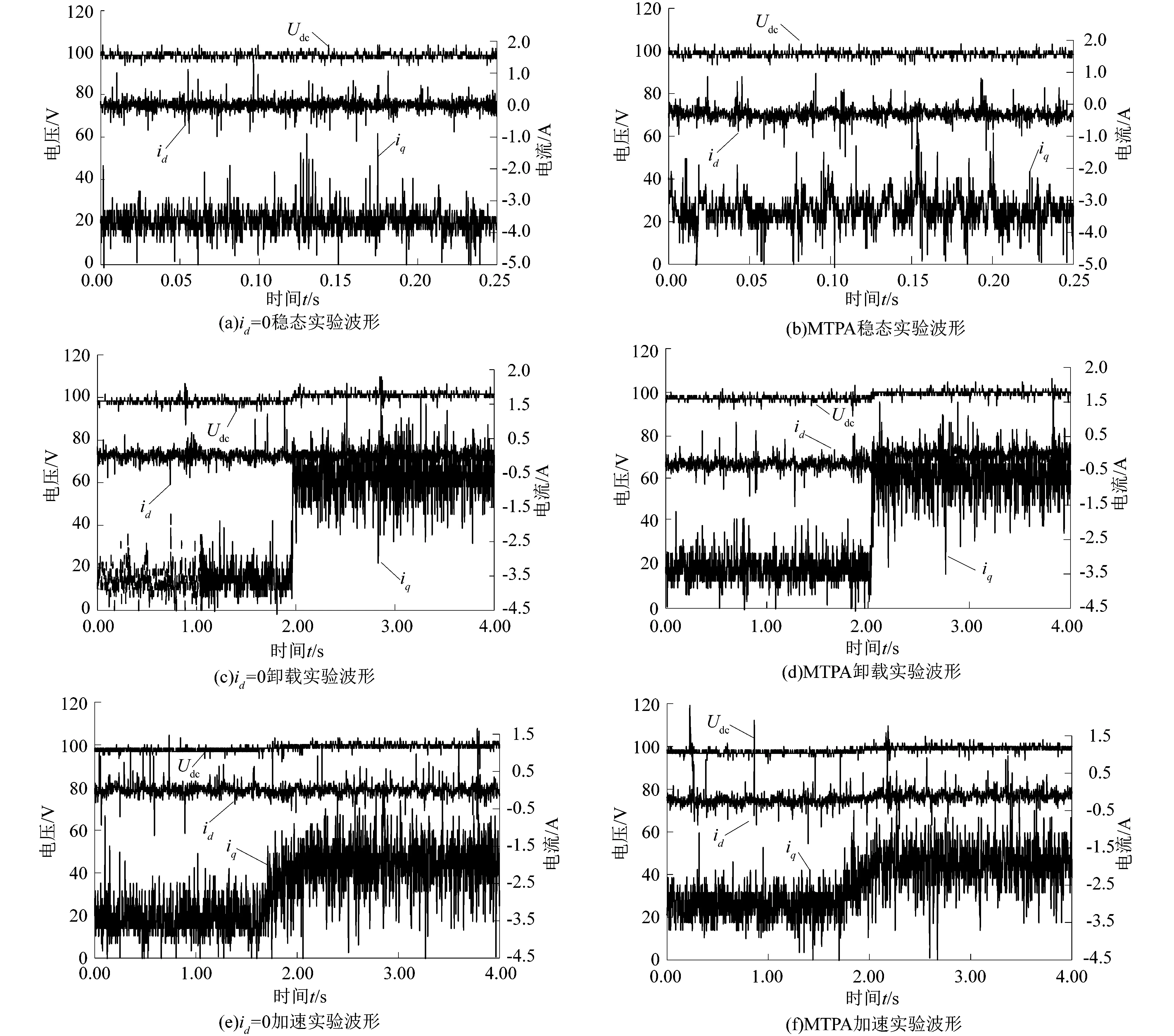
圖8 PMSG基于電流模型預測的id=0控制和基于多目標FCS-MPC的MTPA控制的實驗波形Figure 8 Experiment waveforms of PMSG id=0 control based on current model prediction and MTPA control based on multi-objective FCS-MPC

由圖8(a)和(b)可知，當系統處于穩態時,直流電壓均能較好地穩定在給定值，采用多目標FCS-MPC方法進行控制時，id=-0.25 A,且通過id，iq計算定子電流幅值ia=3.3 A，小于id=0控制時的3.7 A，有效實現了永磁同步發電機整流系統的MTPA控制。

對比圖8(c)和(d)得到：在卸載實驗中，系統突卸負載后，通過課題組提出方法進行控制，id變為0 A且基本穩定在0 A，并能有效跟蹤直流電壓給定，動態響應平滑。

對比圖8(e)和(f)可知：在加速實驗中，原動機突增轉速后，通過多目標FCS-MPC方法，電壓仍穩定在給定值，id仍為負值，仍實現了系統的MTPA控制，由于原動機加速過程的影響，響應速度與仿真有差距，但動態響應平滑，證明MTPA優化有良好的動靜態性能。

6 結語

課題組提出了一種基于多目標FCS-MPC實現永磁同步發電機MTPA控制的方法，通過設計基于MTPA曲線的代價函數，無需實時計算得到MTPA曲線上的id，iq數值，直接實現MTPA控制的FCS-MPC，并與基于電流模型預測的id=0控制進行比對，進行了仿真分析和實驗驗證。仿真和實驗結果表明，通過多目標FCS-MPC，可以實現電磁轉矩跟蹤、MTPA優化控制及最大電流約束，從而有效跟蹤給定直流母線電壓。該方法既能優化系統的運行效率，又使系統具有良好的穩定性，并且動態響應迅速平滑，實現了永磁同步發電機的MTPA控制。