基于矩陣半張量積的信息物理融合系統狀態不透明性分析與控制

張志鵬 許 倩 夏承遺

(天津理工大學智能計算機及軟件新技術天津市重點實驗室 天津 300384)

(天津理工大學學習型智能系統教育部工程研究中心 天津 300384)

1 引言

隨著信息通信技術的飛速發展和數據處理能力的不斷提高，物理系統通過信息通信網絡實現互聯的趨勢日益顯著，由此產生了信息物理融合系統(Cyber Physical Systems, CPSs)。同時，為了提高CPSs的智能化和信息化，系統將部分或全部計算和決策上傳到云服務器中。此時，物理系統的操作環境變得更加開放，為入侵者竊取隱私和機密信息提供了更多的漏洞。因此，隱私分析與安全控制是CPSs領域一個非常重要的研究方向[1,2]。

不透明性作為一種重要的隱私信息流概念，要求入侵者無法準確地推斷出系統的隱私和秘密信息[3,4]。如果一個系統被判定為不透明的，則系統的隱私信息能夠得到有效保證。不透明性的分析和控制問題主要集中在兩個方面：一個是驗證，即判定給定系統是否不透明的；另一個是綜合，即如何通過控制策略保證系統的不透明性。具體地，文獻[5]首次引入當前狀態不透明性的概念，并構建了狀態觀測器對基于狀態的不透明性進行驗證；文獻[6]通過構造K步時延狀態估計器，提出K步不透明性的驗證方法；同時，文獻[7]分析了無窮狀態估計器的性質，證明了無窮步不透明性的驗證問題是一個多項式空間難 (Polynomial SPACE hard ,PSPACE-hard)問題。除此之外，針對上述狀態不透明性的驗證問題，學者提出了多種技術方法和算法，比如雙向觀測器[8]、互模擬法[9]和系統狀態變換法[10]。以上工作主要利用形式化方法展開研究，得到了很多非常深刻且有意義的結論。但是，隨著傳統代數狀態空間理論的發展，基于矩陣半張量積(Semi-Tensor Product, STP)的代數方法為不透明性分析、驗證與控制提供了非常便捷的工具。STP理論最早是由我國控制科學專家程代展教授及其團隊提出的[11-13]，作為常規矩陣乘積的推廣，已得到了廣泛的應用，包括布爾網絡[14-19]、離散事件系統[20-23]、博弈論[24]等多個領域。文獻[25]首次將STP應用于有限自動機系統，提出了有限自動機的代數建模以及狀態可達性等基本問題；文獻[26]基于STP系統地研究了有限自動機的狀態反饋鎮定和輸出反饋鎮定問題，并提出相應的鎮定充要條件和鎮定設計算法；文獻[27]利用布爾STP研究了有限狀態機在有界通信延遲下的網絡化不透明性，給出了在有界通信延遲下的當前狀態估計器動力學方程。另外，STP在離散事件系統中其他研究問題可參考相關文獻[28-30]。

目前，基于STP理論的CPSs的信息安全與隱私防護研究仍處于起步階段。本文針對有限自動機建模的CPSs，提出一種新的代數方法來驗證系統的狀態不透明性。首先，在布爾STP框架下，對CPSs進行代數建模，給出系統動態的代數表達式；其次，假定外部入侵者了解系統結構和狀態轉移等完全信息，構建了CPSs的當前狀態估計器，并提出一個有效的矩陣計算方法；最后，通過引入矩陣的行、列邏輯運算，將系統當前轉移狀態的估計進行簡化，給出判定系統當前狀態不透明性的充分必要條件。本文的主要創新點可凝練為以下3點：

(1) 借助矩陣的布爾STP，通過將狀態/輸入表示為列向量，將有限狀態入侵估計器的轉移函數表示為狀態-轉移估計矩陣，進而得到入侵估計器的可觀測動態演化代數方程。

(2) 結合布爾STP計算特性，入侵狀態-轉移估計矩陣將抽象的當前狀態不透明性驗證問題轉化成較為具體的結構矩陣計算和對應元素判斷問題。

(3) 利用系統演化代數方程和入侵狀態-轉移估計矩陣，給出驗證帶有不可觀事件CPSs當前狀態不透明性的代數充分必要條件。

本文其余部分組織如下，第2節介紹STP和CPSs的相關預備知識；第3節在STP框架下，建立基于有限自動機的CPSs可觀測動力學代數表達式，并提出基于代數狀態空間的不透明性驗證條件；同時，為便于閱讀，針對一些關鍵結論，通過數值算例進行詳細說明。最后，第4節對該文進行總結，并給出后續研究展望。

2 預備知識

本節主要展示了一些常用符號如表1所示，引入了布爾矩陣半張量積的定義、常用性質及具體算例。同時，介紹了本文用到的信息物理系統模型，即帶有不可觀事件的不確定有限自動機。

表1 常用符號

2.1 半張量積

近年來，程代展教授及其團隊提出的基于STP的代數狀態空間方法逐漸發展成為邏輯系統分析和設計有力的工具之一。該方法擴大了矩陣的適用范圍，同時，還保持了矩陣普通乘法的所有重要性質。鑒于STP理論的優點，將該方法引入到CPSs的不透明性分析問題中。

首先，給定矩陣A=(aij)a×b ∈Ra×b和B=bijc×d∈Rc×d，它們的克羅內克積是維度為ac×bd的分塊矩陣

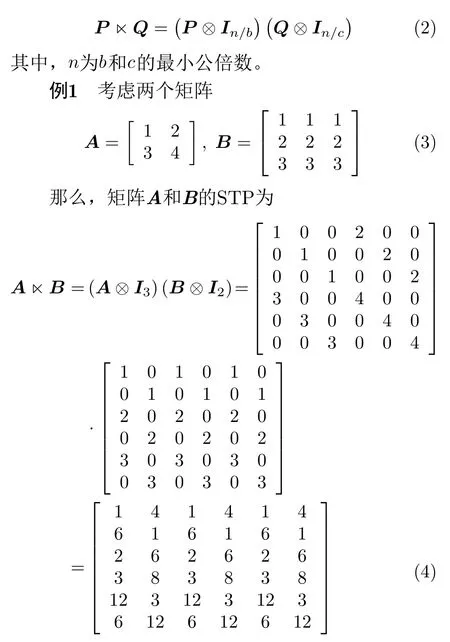
在有限邏輯系統中，許多分析和控制問題更關注經過STP運算后矩陣中的元素是“0”還是“1”。以有限自動機的可控性為例，只需要檢測初始狀態到目標狀態是否可達的，不需要知道可達路徑的條數。因此，為便于計算和矩陣表示，在矩陣STP中引入布爾運算，得到了布爾STP的定義。

2.2 基于有限自動機的CPSs與狀態不透明性

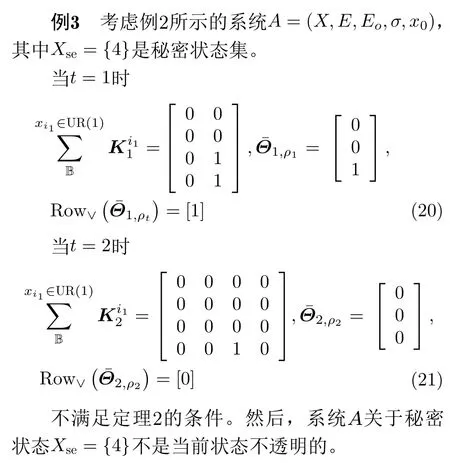
在現實中，很多CPSs的狀態的變遷是由事件驅動的，而且往往會出現同一個事件產生多個不確定的狀態轉移。針對這些情況，本文引入有限自動機模型對上述現象進行刻畫。本節介紹了關于有限狀態自動機的基礎概念和相關記號。

基于狀態的不透明性描述了系統隱私和秘密狀態轉換的行為信息流，是信息安全理論和技術的一個重要概念。對于給定的秘密狀態集Xse?X和系統生成的任意事件串L(A)，如果外部的惡意入侵者不能確定地推斷出系統當前所處狀態是否是秘密狀態x ∈Xse，則該系統被認為是狀態不透明的。假設入侵者具有以下能力：

(1) 入侵者完全了解系統的結構和事件轉換。

(2) 系統A生成的語言是非死鎖的，即A中的每個狀態都存在一個轉移事件。

3 基于STP的當前狀態不透明性的分析與驗證

3.1 系統入侵下的當前狀態估計

定理1 給定系統A=(X,E,Eo,σ,x0)，外部入侵條件下的動力學方程可描述為

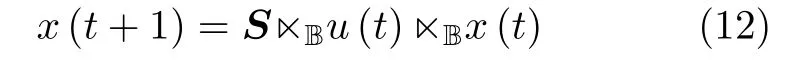
其中，x(t)表示從x(1)出發在t時刻系統當前狀態估計的向量表達式，u(t)表示在t時刻可觀測事件的向量表示。

證明過程略，可參考文獻[25]進行證明。

事實上，上述定理揭示了入侵估計器的動態轉換可用代數方程來表示，并且建立了一步可觀測事件的動態轉移。接下來，通過定理1中矩陣表達式的重復迭代運算，可得到系統從x(1)出發在t時刻系統當前狀態估計的向量表達式為

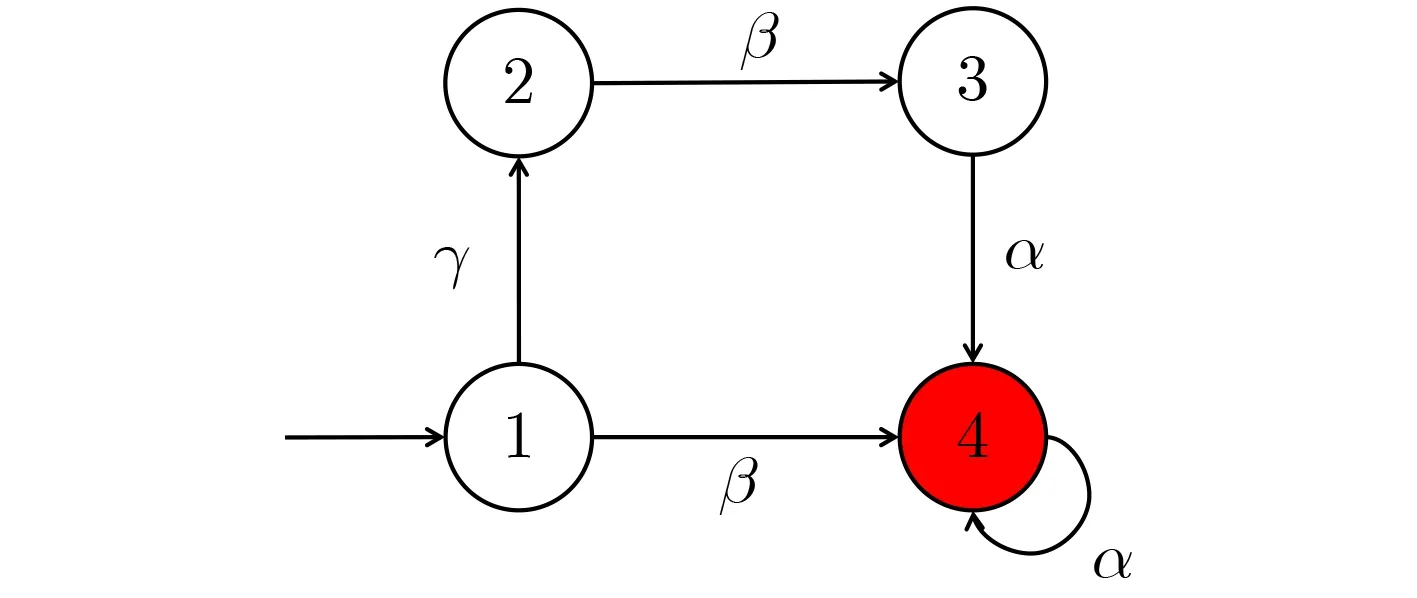
圖1 系統A=(X,E,Eo,σ,x0)

3.2 當前狀態不透明的驗證

基于上述入侵部分觀測條件下的狀態估計模型，本節集中對系統的當前狀態不透明性進行分析與驗證。首先，給出系統當前狀態不透明性的定義如下。

定義3 考慮系統A=(X,E,Eo,σ,x0)以及秘密狀態集Xse?X，

(1) 如果σ(x0,s)∩Xse?=?，那么字符串s ∈E?是秘密-可達的；

(2) 如果σ(x0,t)∩{X ?Xse}?=?，那么字符串t ∈E?是非秘密-可達的；

(3)A稱為關于Xse不透明的，如果對于任意的秘密-可達串s，總存在另一個非秘密-可達串t使得P(s)=P(t)。

值得注意的是，入侵者往往通過系統模型結構和可觀事件轉移來獲得系統的狀態估計，根據上述狀態不透明性定義，對于任意一個字符串，如果該串驗證為秘密-可達的，則至少存在另一個具有相同入侵觀測映射的非秘密-可達的字符串，進一步使得入侵者在當前時刻無法判斷當前到達的狀態是否是秘密狀態，此時，具備狀態不透明性的系統能夠保證入侵者總是不能揭露系統的秘密信息。因此，狀態不透明性對于系統信息安全與隱私的分析與控制具有非常重要的意義。

為了進一步理解所提方法的計算過程以及提高該文的可讀性，算法流程的整體闡述如圖2所示。

圖2 驗證算法的流程圖

在實際工程中，設計者往往更關注哪些路徑或者轉移序列違反了狀態不透明性，以便于采取措施進行校正，進而防止隱私信息的泄漏。定理2表明如果系統是當前狀態不透明的，當且僅當Row∨

進一步地，根據矩陣STP的運算特性(引理3)，可計算出其對應事件。通過上面定理，可知系統狀態不透明性的判定可以轉換成邏輯代數的運算，這為更多類型的狀態不透明性的驗證以及其強化監督控制提供了有效的工具。

備注2 定理2給出了一種基于矩陣的方法來驗證有限自動機的當前狀態不透明性。相較于現存方法，有以下兩方面不同之處：

(1) 在研究問題上，本文提出的代數框架為研究CPS的基于狀態的各種不透明屬性提供了新的研究思路與視野。

(2) 在研究方法上，矩陣半張量積是我國學者開創性的數學成果，基于此提出驗證給定CPS不透明性的方法易計算，同時推廣了矩陣半張量積的應用范疇。

本文所提方法具有以下特點：首先，借助矩陣的布爾STP，建立了一種描述入侵估計器動態演化的算法，并基于該代數表達式，簡潔明了地導出了不透明性的驗證準則，為研究復雜CPSs的分析和控制問題，特別是相關的隱私和安全保護問題提供了新的視角。其次，借助矩陣半張量積Matlab軟件包，不透明性的驗證問題可以相應地轉換成矩陣求解問題。最后，上述結果在未來有望擴展到更復雜的系統[31,32]。

4 結束語

本文針對帶有不可觀測事件的不確定有限自動機建模CPSs，提出一種基于矩陣STP的外部入侵動力學代數方程，并通過矩陣的布爾邏輯運算給出驗證當前狀態不透明性的充分必要代數條件，為進一步分析其他類型的狀態不透明性以及基于狀態不透明性強化控制問題提供了一個非常有益的視角。此外，數值算例驗證了該方法的有效性。未來的研究方向包括以下兩個方面：一方面，當原始系統不是狀態不透明時，如何設計一些監控與強化策略來確保不透明性是非常重要的研究問題；另一方面，當前工作假設有限自動機的權重都為1，然而現實系統中事件的轉移權重往往是不一樣的，因此推廣所提方法到加權有限自動機的隱私分析與控制問題具有非常重要的工程意義。