無人機基站的飛行路線在線優化設計

張廣馳 嚴雨琳 崔 苗* 陳 偉 張 景

①(廣東工業大學信息工程學院 廣州 510006)

②(廣東省環境地質勘查院 廣州 510080)

③(中國電子科學研究院 北京 100043)

1 引言

在過去的十年中，由于無人機(Unmanned Aerial Vehicle, UAV)移動性高、成本低等特點，無人機在無線通信領域引起了廣泛的關注[1]。無人機在即將到來的5G通信時代也會發揮重要的作用，主要可以分為兩類。第1類，無人機可以作為空中移動的通信平臺輔助地面基站的通信。無人機基站可以為超密集網絡的地面基站提供補充覆蓋，也可以利用空地信道增益大的優勢為毫米波通信提供高增益的無線連接。在應對自然災害緊急救援情況時，無人機基站可以臨時代替被損壞的地面基站提供應急通信。在基礎設施覆蓋不足的地區，無人機基站可以作為中繼為地面用戶提供無線通信服務。在熱點區域或者需要處理臨時事件期間，無人機基站能夠為網絡流量擁塞的地面基站提供有效的業務分流。第2類，無人機作為空中的用戶，接入到地面的蜂窩通信網絡。未來5G蜂窩網絡能夠為無人機提供更加可靠、更加安全和超低時延的連接從而實現其更多功能[2-6]。文獻[3]研究了無人機通信網絡中物理層安全性的問題；文獻[4]研究了多無人機基站通信網絡中的軌跡優化和功率分配問題；文獻[5]研究了無人機中繼系統中通過軌跡優化和功率分配來最大化吞吐量的問題。

本文主要研究的是上述第1類應用場景，即無人機作為空中基站為地面用戶提供無線通信服務。相比于傳統的地面基站，無人機基站的飛行高度比較高，能夠與用戶建立更加可靠的通信鏈路[4]，能夠適應突發情況下的通信場景，例如救援、搜索、熱點區域覆蓋等。目前大多數的研究是通過優化無人機的位置部署、無人機的飛行軌跡或者資源分配來達到更佳的通信質量。例如文獻[7]研究了最小化無人機基站的數量以及部署無人機的位置來覆蓋給定數量的地面用戶；文獻[8]研究了無人機輔助的無線傳感網中的數據采集；文獻[9]研究了多跳無人機中繼通信系統的軌跡優化以及功率分配。上述文獻中采用的算法都屬于離線優化算法，建立在對通信環境的完美假設的基礎上，在無人機起飛之前規劃好無人機的軌跡。然而在實際中，通信環境是不斷變化的，無法提前預測，通信環境的完美假設無法實現[10]，因此無法解決地面用戶隨機的通信請求問題。與離線優化算法不同，在線優化算法不需要在無人機起飛前提前設計好無人機的飛行路線，而是能夠在飛行過程中根據通信環境的變化動態、連續地規劃無人機的飛行路線。文獻[11]提出了一種近似動態規劃的無人機機動決策方法；文獻[12]提出一種基于動態規劃的在線優化算法，而動態規劃需要一個環境模型，且計算復雜度較高。

為了讓無人機基站具有動態、實時規劃飛行路線的能力，從而實現飛行路線能夠實時適應地面用戶隨機的通信請求，并且考慮到無人機基站與地面用戶進行時效性較強的決策信息通信時，減小通信時延尤為重要。本文將從平均通信時延最小化的角度出發，提出基于強化學習的飛行路線在線優化設計算法。在線優化算法能夠在飛行過程中根據通信環境的變化動態地規劃無人機的飛行路線，不需要完備的通信環境參數且計算復雜度比動態規劃的低。強化學習方法包含蒙特卡羅和Q-Learning兩類算法，用于解決馬爾可夫決策問題[13]。實踐證明，強化學習算法具有解決無人機無線網絡在線優化問題的能力，例如文獻[14]研究了多無人機輔助蜂窩網絡中的用戶體驗質量(Quality of Experience,QoE)；文獻[15]研究了多無人機輔助蜂窩網絡中所有用戶的通信速率和最大化的問題。

本文研究一個無人機空中基站為兩個地面用戶提供無線通信服務，其中地面用戶的通信請求是隨機的，以平均通信時延最小化為目的來設計無人機的在線飛行路線。首先，把飛行路線設計問題轉化成一個馬爾可夫決策過程，根據地面用戶的通信請求情況和無人機的位置把無人機的狀態分為通信狀態和等待狀態，然后定義不同狀態下的動作集，將無人機完成單次任務的通信時延設置為回報，采用強化學習的蒙特卡羅算法以及Q-Learning算法實現在線優化無人機飛行路線。最后，通過計算機仿真驗證本文提出的算法的有效性。

2 系統模型

如圖1所示，本文考慮一個無人機基站通信系統，其中包括有一個無人機和兩個地面用戶1)本文主要研究無人機基站的飛行路線在線優化，主要考察飛行路線對通信性能的影響，沒有考慮無人機基站的能耗問題。另外，本文考慮的系統模型同樣適用于多個無人機基站分別在不同頻段上與地面用戶通信的場景，并且后文提到的優化算法可以直接擴展到多個地面用戶處在一條直線上的場景。。無人機作為一個空中通信基站，為兩個地面用戶提供無線通信服務。假定兩個地面用戶的通信請求是隨機的，它們獨立同分布，服從均值為λ/2的泊松過程(λ/2次請求/秒)，每次通信請求的傳輸信息量為Lbit，地面用戶1位置坐標為(?a,0,0)和地面用戶2的位置坐標(a,0,0)。假設無人機的飛行高度固定為H，最大飛行速度為Vmax，無人機在兩個地面用戶所連接的線段間移動。定義無人機單次完成傳輸任務的時間為T，稱為單次通信時延，在時刻t無人機的位置坐標為q(t)=(x(t),y(t),H),x(t)∈[?a,a],y(t)=0。因為地面用戶的位置都在X軸上，無人機為了獲得更好的通信鏈路需要盡可能靠近地面用戶，所以無人機的飛行路線也在X軸。

圖1 無人機基站通信系統

無人機收到地面用戶r ∈{1,2}的通信請求之后，進入通信狀態，此時無人機為地面用戶提供無線通信服務，其他地面用戶的通信請求會被忽略。在完成數據傳輸之后，無人機進入等待狀態，開始等待下一次通信請求，這個過程一直重復。

由于無人機的飛行高度比較高，與地面用戶的鏈路與視距信道相似，所以本文假設無人機與地面用戶之間的通信鏈路為視距信道[16]，無人機的發射功率固定為P，在t時刻，無人機與地面用戶之間的瞬時通信速率為

3 飛行路線在線優化設計算法

3.1 問題描述

其中，q′(t)表示無人機的速度V。式(2a)是保證在第m次通信任務中，Tm時間內能夠傳輸Lbit的信息；式(2b)表示無人機的飛行速度的約束，無人機的速度可取0或者Vmax；式(2c)是對無人機的位置約束。很明顯(P1)是一個非凸的問題，同時為了讓無人機基站具有動態、實時規劃飛行路線的能力，從而適應不可預測、隨機的地面用戶通信請求，所以本文提出無人機飛行路線在線優化設計算法。所提算法基于強化學習的思想。

3.2 強化學習概述

將(P1)問題中無人機的軌跡離散化重新表述成一個馬爾可夫決策過程。(P1)對應的馬爾可夫決策過程如下：

3.3 最小單次通信時延

很明顯lp1,p2=lp2,p1,lp1,p2=l?p1,?p2。

接下來證明單次通信時延最小的飛行路線的存在，假設無人機與地面用戶1通信，對于任意一條軌跡q(·)∈A1(qi →qj)，時延為Δt，可以找到另外一條軌跡q^(·)∈A1(qi →qj)，時延同為Δt，滿足|q(t)?x1|≥|q^(t)?x1|,?t ∈[0,Δt]，無人機在q^(·)軌跡下總是比在q(·)軌跡下更靠近地面用戶1。因此在相同通信時延的情況下，無人機在q^(·)軌跡下總是比在q(·)軌跡下能夠傳輸更大的信息量。換句話說，當無人機的通信狀態的起始位置和結束位置相同時，q^(·)更靠近地面用戶1，獲得更好的通信鏈路，從而減小通信時延。同理，無人機與地面用戶2通信的情況相同。

3.4 基于蒙特卡羅的在線優化設計算法

蒙特卡羅算法通過平均樣本的回報來解決強化學習問題。為了保證能夠具有良好定義的回報，本文采用用于分幕式任務的蒙特卡羅算法。智能體與環境的交互分成一系列子序列，將子序列稱為幕，每幕從某個標準起始狀態開始，并且無論選取怎樣的動作整個幕一定會終止，下一幕的開始狀態與上一幕的結束方式完全無關，具有這種分幕特性重復任務稱為分幕式任務。價值估計和策略改進在整個幕結束之后進行，因此蒙特卡羅算法是逐幕做出改進的。蒙特卡羅算法是從任意的策略π0開始交替進行完整的策略評估和策略改進，最終得到最優的策略和動作價值函數。策略評估的目標是估計動作價值函數Qπ(s,a)，即在策略π下從狀態s采取動作a的期望回報。策略改進是在當前的動作價值函數上貪婪地選擇動作。由于已經存在動作價值函數，所以在貪婪的時候完全不需要使用任何的模型信息。對于任意的一個動作價值函數，對于任意的貪婪策略為：對于任意一個狀態s ∈S，必定選擇對應動作價值函數最大的動作，π(s)=arg maxaQ(s,a)[13]。在每一幕結束后，使用觀測到的回報進行策略評估，然后在該幕序列訪問到的每一個狀態上進行策略的改進。本文采用的是基于試探性出發的蒙特卡羅算法，具體算法如下：

步驟1 初始化最大訓練幕數Nepi，每幕中最大步數Nstep，對于所有s ∈Scomm，任意初始化；對于所有s ∈Scomm，a ∈A?r(qi)任意初始化動作值函數Q(s,a)∈R；

步驟2 隨機選擇s0=(i,r)，根據π生成一幕序列：s0,a0,R1,s1.a1,...,sNstep?1.aNstep?1,RNstep；

步驟3G=0；計數變量W=0；Nepi=Nepi?1；

步驟4 對幕中的每一步循環，n=Nstep?1,Nstep?2,...,0：

文獻報道顯示絕大多數神經系統的癥狀和體征是一過性的，于數周或數月可完全恢復［8］。但脂肪栓塞綜合征治療成功的關鍵在于早期診斷、綜合對癥支持治療。尚無特異性溶脂治療方法，主要是對肺、腦等器官的保護。目前通過（1）骨折部位的早期固定及固定方式的改變［2］；（2）預防性使用激素來減少脂肪栓塞綜合征的發生。甲潑尼龍是目前最常使用的激素，劑量范圍為 6～90 mg/kg［1,9］。

當二元組sn,an在s0.a0,s1.a1,...,sNstep?1.aNstep?1中出現過，退出幕中循環。

步驟5 重復步驟2-步驟4，直到Nepi=0。

3.5 基于Q-Learning的在線優化設計算法

與前面提到的蒙特卡羅算法一樣，時序差分算法也可以直接從環境互動的經驗中學習策略。時序差分算法與蒙特卡羅方法不同，不用等到交互的最終結果，而是在已得到的其他的狀態估計值來更新當前狀態的價值函數，其價值估計和策略改進是逐步的。與蒙特卡羅算法相比，時序差分算法的優勢在于它運用了一種在線的、完全遞增的方法來實現。蒙特卡羅算法必須等到一幕的結束才能知道確切的回報值，而時序差分算法只要等到下一時刻即可[13]。因為本文系統模型中的地面用戶的通信請求是逐個發送的，然后由無人機逐個完成的，所以采用時序差分算法更加適合。本文采用的Q-Learning是一種典型的強化學習時序差分算法，動作價值函數定義為Q(sn,an)=Q(sn,an)+α[rn+1+γmaxaQ(sn+1,a)?Q(sn,an)]，其中α ∈(0,1]為步長，權衡上一次學習的結果和這一次學習的結果；γ ∈[0,1]為折扣率，是考慮未來回報對現在影響的因子，γ的值越大，說明未來回報對現在影響越大；具體如下：

步驟1 初始化探索參數ε，最大訓練幕數Nepi，每幕中最大步數Nstep，動作價值函數Q(s,a)=0,?s ∈Scomm,?a ∈A?r(qi)；

步驟2 隨機給定初始狀態s0=(i,r)；

步驟3Nepi=Nepi?1；

步驟4 對幕中的每一步循環，n=1,2,...,Nstep：

更新動作價值函數，Q(sn,an)=Q(sn,an)+α[rn+1+γmaxaQ(sn+1,a)?Q(sn,an)]；

步驟5 重復步驟2-步驟4，直到Nepi=0。

4 仿真結果

本節利用計算機仿真對上述所提的飛行路線在線優化算法進行驗證，并對比兩種基準方案“固定位置”和“貪婪算法”。“固定位置”為無人機懸停在兩個地面用戶的連線的中點，“貪婪算法”的描述為在無人機每次進入通信狀態(i,r)時，選擇最小單次通信時延的飛行路線，即通信狀態的結束位置qj。

仿真中采用的系統參數為：地面用戶1和地面用戶2相距800 m，其中地面用戶1的位置坐標為(?400 m,0,0)，地面用戶2的位置坐標(400 m,0,0)；兩個地面用戶的通信請求到達率λ=1 次/秒，傳輸的信息量L=2 Mbit，無人機的飛行高度H=100 m，最大飛行速度Vmax=20 m/s，信道帶寬B=1 MHz，參考距離1 m時的信噪比γdB=40 dB。將無人機的可飛行區域分為2N+1=101個位置狀態，其他參數：Nepi=120,Nstep=10000,ε=0.1,α=1,γ=0.2。

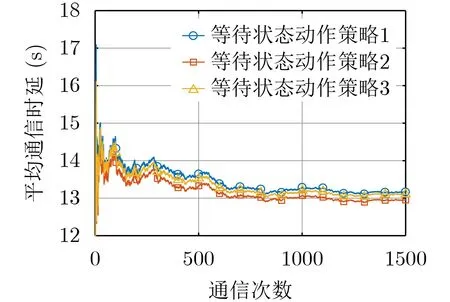
圖2 等待狀態時采取不同動作策略的平均通信時延

在以下的仿真中，無人機的等待狀態都采取等待狀態動作策略2。

圖3展示了不同算法下的無人機平均通信時延，可以看出相比于“固定位置”，其他3種算法下的平均通信時延都比較小，其中基于Q-Learning的在線優化設計算法的平均通信時延最小。這是因為“貪婪算法”只考慮當前的回報，沒考慮長期回報；而蒙特卡羅算法把學習推遲到整幕結束之后，必須等到每一幕的結束，才能知道確切的回報值，而Q-Learning算法在每個動作結束就能夠知道回報值從而進行學習，本文中的問題是一個持續性任務，不適合分幕式任務的蒙特卡羅算法，更加適合用Q-Learning算法來解決。

圖3 不同算法下的無人機平均通信時延

圖4展示在不同的傳輸信息量下，采用不同算法得到的平均通信時延。可以看出基于Q-Learning的在線優化設計算法的平均通信時延始終優于基于蒙特卡羅算法和“貪婪算法”的在線優化設計算法。傳輸信息量越大，基于Q-Learning的在線優化設計算法的時延性能越好。

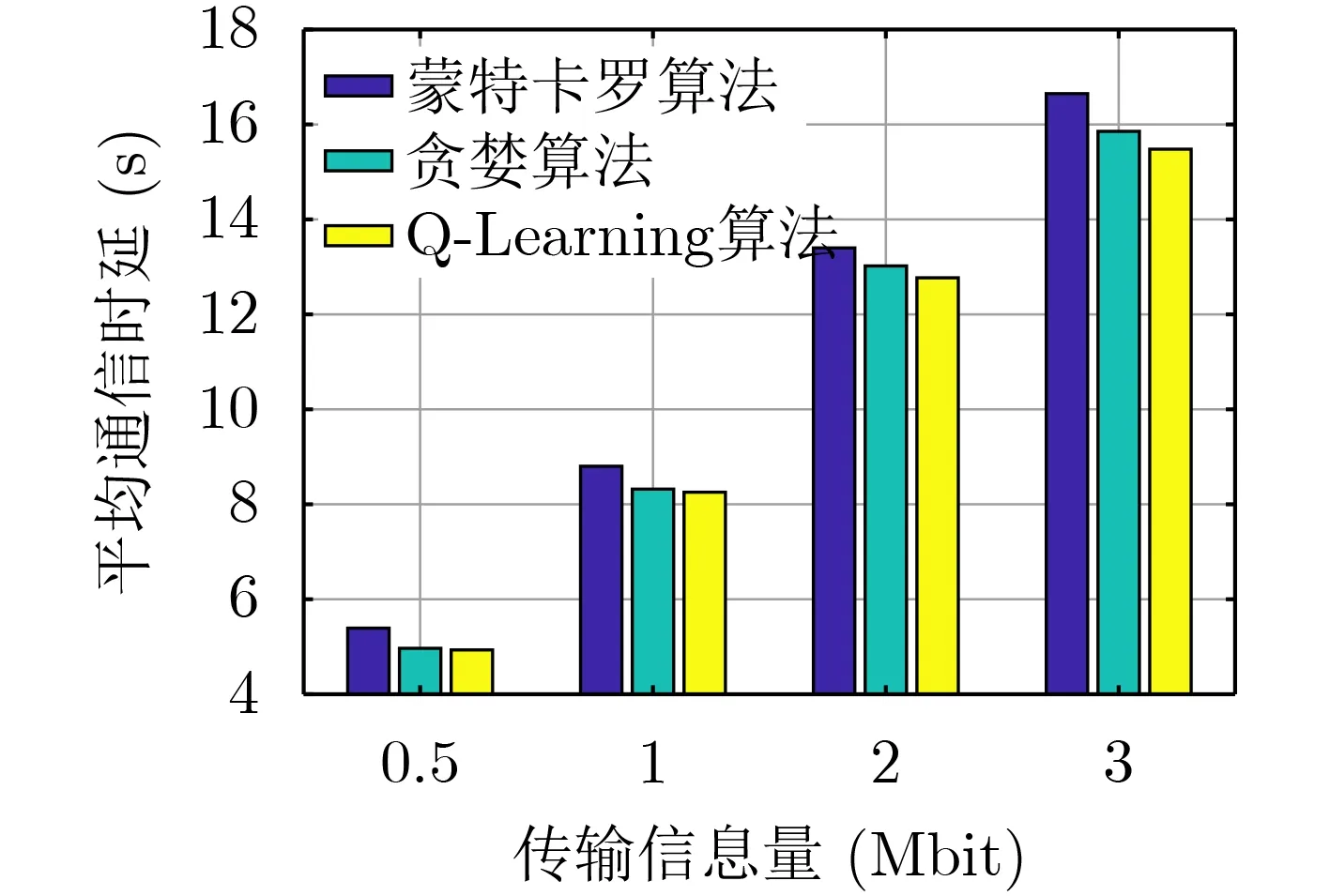
圖4 不同傳輸信息量以及不同算法下的無人機平均通信時延

圖5展示了基于Q-Learning的在線優化設計算法和基于蒙特卡羅算法的在線優化設計算法下的平均通信時延隨著訓練幕數增大而逐漸收斂，可以看出基于Q-Learning的在線優化設計算法要比基于蒙特卡羅算法收斂得更快且穩定。

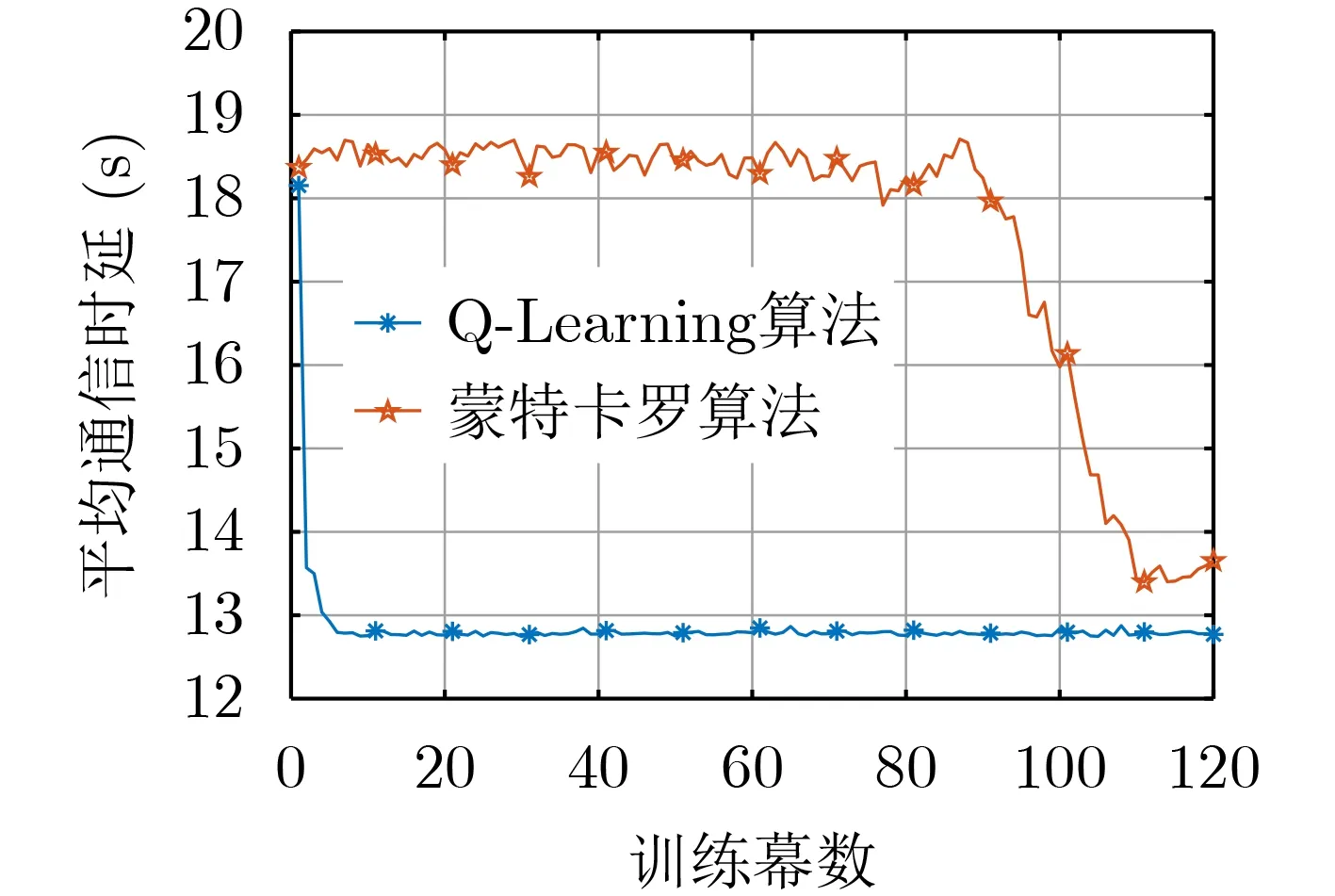
圖5 不同算法的收斂程度

圖6和圖7分別展示了基于Q-Learning算法和基于蒙特卡羅算法的在線優化設計算法下無人機連續的10個狀態下的飛行路線，其中無人機的起點是隨機的，無人機的狀態是根據地面用戶的通信請求變化的，兩個地面用戶通信請求分別服從均值為1/2的泊松過程。圖6和圖7中的無人機狀態：0表示無人機處于等待狀態，1表示接收到地面用戶1的通信請求，2表示接收到地面用戶2的通信請求；時長表示無人機處于當前狀態采取的動作所耗費的時間。可以對比看出基于Q-Learning的在線優化設計算法的無人機飛行路線更加集中于兩個地面用戶的中點，說明基于Q-Learning的在線優化設計算法更加能適應隨機的地面用戶請求，從而得到更小的平均通信時延。

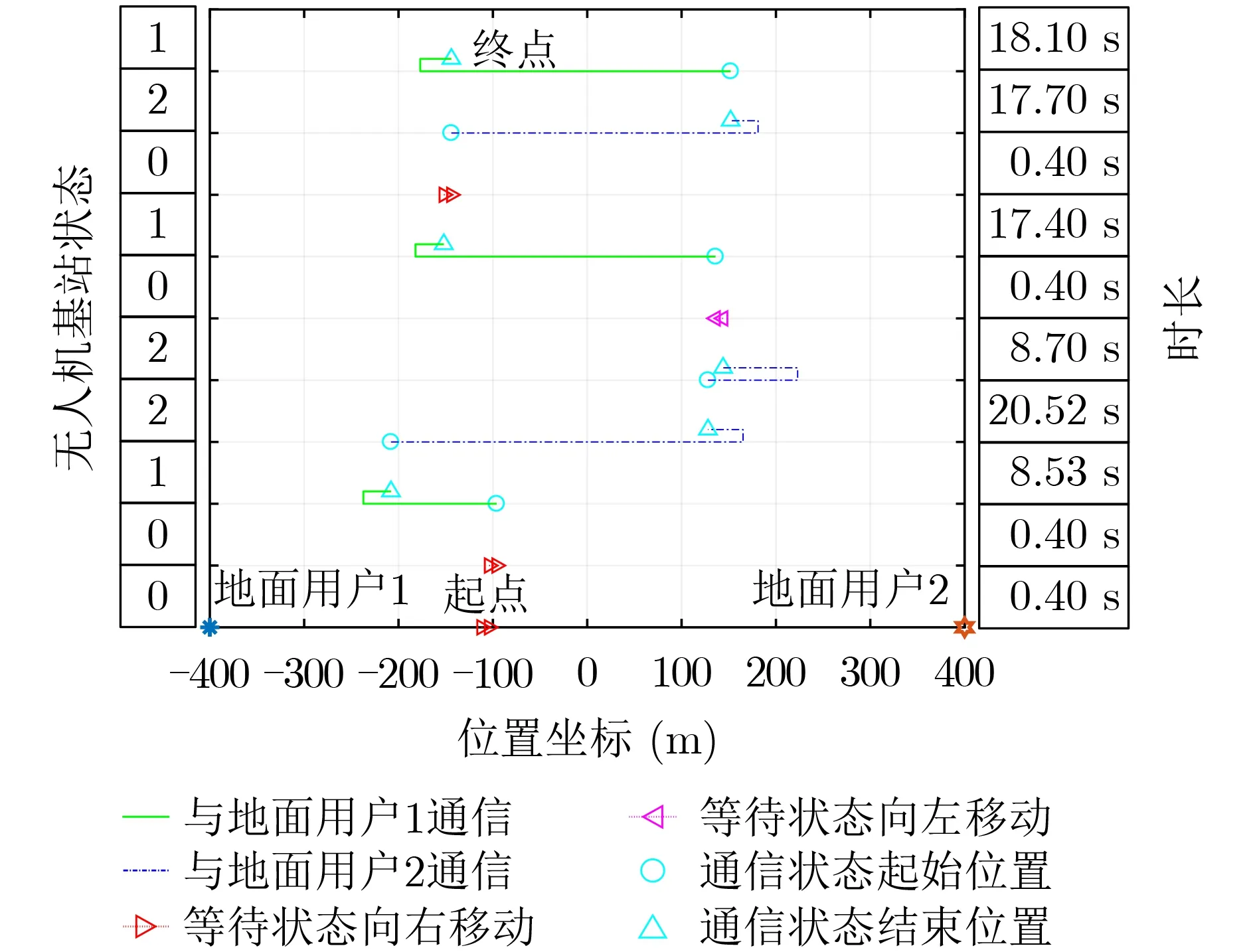
圖6 基于Q-Learning的在線優化設計算法下無人機飛行路線

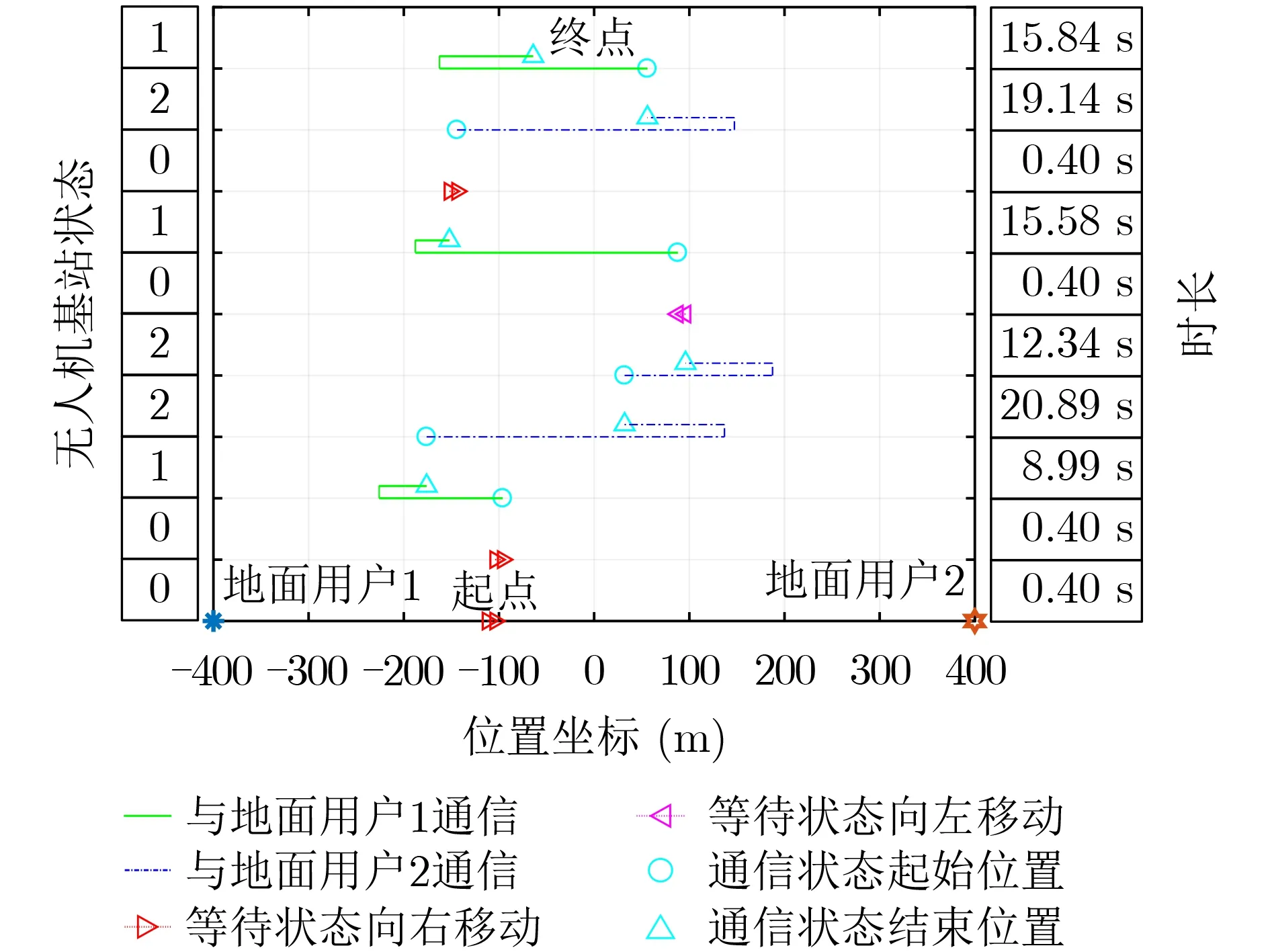
圖7 基于蒙特卡羅的在線優化設計算法下無人機飛行路線

5 結束語

本文針對無人機基站通信系統，提出了兩種基于強化學習的無人機飛行路線在線優化設計算法。分別采用了強化學習的蒙特卡羅算法和Q-Learning算法來最小化無人機的平均通信時延。仿真結果顯示了與無人機在固定位置相比，提出的算法具有較好的性能。基于Q-Learning的在線優化設計算法比基于蒙特卡羅的在線優化設計算法的訓練結果更快收斂且穩定，能夠更好地適應隨機的地面用戶請求從而達到更小的平均通信時延。