非均勻噪聲條件下的互質陣列欠定DOA估計方法

孫 兵 阮懷林 吳晨曦 鐘 華 吳世龍

(國防科技大學電子對抗學院 合肥 230037)

1 引言

波達方向(Direction Of Arrival, DOA)估計廣泛應用于雷達信號處理、目標檢測、導航等諸多領域，是陣列信號處理領域的核心研究內容之一。現代電磁環境信源密集且復雜多變，往往需要利用有限的陣元實現多信源測向。經典的超分辨算法多是針對均勻線性陣列設計，自由度受陣元個數限制，由N個陣元組成的均勻陣列的可達到的自由度限制為N ?1，難以實現欠定條件下的DOA估計。為解決這一問題，文獻[1]提出互質陣列結構模型，相較于傳統均勻陣列，N陣元的互質陣列，其自由度可以達到O(N2)。互質陣列之所以具有這一優勢是因為其差聯合陣中擁有大小為O(N2)的虛擬均勻線陣部分。故該理論框架一經提出便受到了廣泛的關注[2-5]。目前，基于互質陣列的欠定DOA估計經典算法主要包括空間平滑算法[6]、稀疏算法[7]和數組插值算法[8]。這些算法均假設噪聲為高斯白噪聲，當噪聲模型不滿足高斯白噪聲時，基于互質陣列的DOA估計算法性能會嚴重下降。在實際應用中，由于陣元間相互耦合、非理想的接收通道以及陣列未校準等因素，相關色噪聲常常出現，一般情況下，相關色噪聲結構未知，但某些情況下，如陣元稀疏布置，色噪聲可以進一步簡化為非均勻噪聲[9-11]。

對于非均勻噪聲條件下的DOA估計問題，文獻[12]對非均勻噪聲進行預白化，進而實現魯棒的DOA估計，但該方法要求陣元數量至少是信源數量的3倍。文獻[13]推導了基于最大似然的DOA估計方法，使用迭代方式估計非均勻噪聲參數，具有很高的計算復雜度。文獻[14]提出了基于子空間的DOA估計方法，但同樣需要迭代過程。文獻[15]提出了一種非迭代方法，從而降低了計算復雜度并避免了收斂問題。但是，文獻[13-15]提出的方法均要求陣元數大于信源數，無法適用于欠定DOA估計。為此，文獻[16]提出一種基于壓縮感知的DOA估計算法，該方法適用于互質陣列，并在文獻[17]進一步擴展到寬帶信號，然而，該方法直接從數據協方差矩陣中刪除了對角線元素，導致性能下降。文獻[18]提出了一種非均勻噪聲條件下的互質陣列DOA估計方法，但該方法僅使用差聯合陣中連續的虛擬陣元，舍棄了非連續部分，因此無法獲得最佳性能。文獻[19]針對非均勻噪聲背景下欠定DOA估計，提出了基于全變分范數最小化的估計方法，但該方法同樣無法利用非連續虛擬陣元。文獻[20]充分利用了所有虛擬陣元，然而，該方法為構造無噪聲協方差矩陣，直接移除采樣協方差矩陣對角線元素，導致對角線元素中的有用信號成分也被移除，造成了信息損失。

針對上述問題，為實現互質陣列在非均勻噪聲條件下的魯棒DOA估計，本文提出一種基于協方差矩陣重構和矩陣填充的DOA估計方法。首先將接收數據協方差矩陣分解，得到包含非均勻噪聲項的對角陣。然后選取對角線元素中的最小值替換其余對角線元素得到重構后的協方差矩陣，實現了噪聲協方差矩陣預白化，并等效提高了信噪比。最后，為實現欠定DOA估計，對重構后的協方差矩陣進行擴展和矩陣填充，結合子空間方法進行DOA估計。相對于現有方法，該方法充分利用了所有虛擬陣元，有效抑制非均勻噪聲的同時不丟失有用信息，提高了估計性能。

2 互質陣列信號模型

互質陣列模型如圖1所示，該陣列由兩個線性均勻陣列組成，子陣1中包含N個陣元，間距為Md。子陣2中包含2M個陣元，間距為Nd，兩個子陣共用第1個陣元。其中，M與N是兩個互質的整數，d=λ/2，λ為入射信號波長。各陣元位置集合可表示為P={nMd,0≤n ≤N ?1}∪{mNd,0≤m ≤2M ?1}。

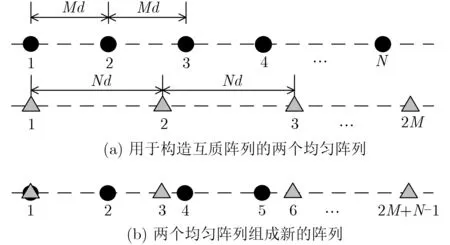
圖1 互質陣列示意圖

假設有L個遠場窄帶信號分別入射至互質陣列，到達角為：θ=[θ1,θ2,...,θL]，則陣列輸出數據可表示為

3 非均勻噪聲條件下的互質陣列DOA估計方法

3.1 差聯合陣列的數據預處理

為了直觀分析互質陣列，給出差聯合陣列概念，定義集合S 為

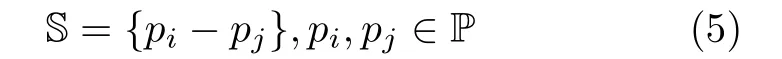
其中， P 為互質陣列各陣元位置集合，pi和pj分別表示第i和第j個陣元位置。S 為各陣元位置差構成的集合， S中存在相同元素值，將S 中所有不同元素值px構成的集合定義為Sx，px在S 中重復出現的次數定義為ω(px)。由互質陣列性質，集合Sx中各元素值即差聯合陣列的虛擬陣元位置，其中非負元素數為陣列自由度，直接決定了互質陣列的最大可估計信號數。

由式(2)可得互質陣列接收數據協方差矩陣

3.2 基于協方差矩陣重構和矩陣填充的DOA估計方法

為了減少非均勻噪聲影響，先對數據協方差矩陣進行重構，將R分解為如下兩個矩陣之和

其中，R1和R2具體表示為

步驟 4 通過式(14)，進一步得到重構后的協方差矩陣R?。

步驟 5 通過式(1 6)將R?擴展成維數為(2MN ?N+1)×(2MN ?N+1)的Toeplitz 矩陣RE。

步驟 6 將RE的矩陣填充問題轉化為式(17)秩函數最小化模型，再利用式(19)核范數最小化對式(17)進行凸松弛，最后基于奇異值閾值算法實現矩陣填充，得到目標矩陣RV。結合MUSIC算法進行DOA估計。

4 仿真實驗

4.1 可行性分析

將所提算法的性能與3種經典互質陣列DOA估計算法進行比較，包括SS-MUSIC算法[6]，COLasso算法[7]和Interpolation算法[8]。設置MUSIC算法的角度搜索間隔為0.1°, CO-Lasso算法的完備字典間隔設置為0.1°。設有1 6 個均勻分布于-42°～48°方向的遠場窄帶信號，信噪比SNR=0 dB，快拍數L=300。非均勻噪聲協方差矩陣Q=diag{31,20,5,13,16,37,1,27,9,13}。4 種算法的實驗結果如圖2所示。

由圖2可以看出，3種經典互質陣列DOA估計算法效果均不理想，其中SS-MUSIC算法只能對少數信源實現DOA估計，CO-Lasso算法和Interpolation算法對于部分信源估計誤差較大，而本文算法可以對全部信源進行較準確的DOA估計。這是因為3種經典算法的基本假設是均勻白噪聲背景下，而在非均勻噪聲情況下，估計性能下降，本文通過對接收數據協方差進行矩陣重構和填充，有效地抑制了非均勻噪聲。

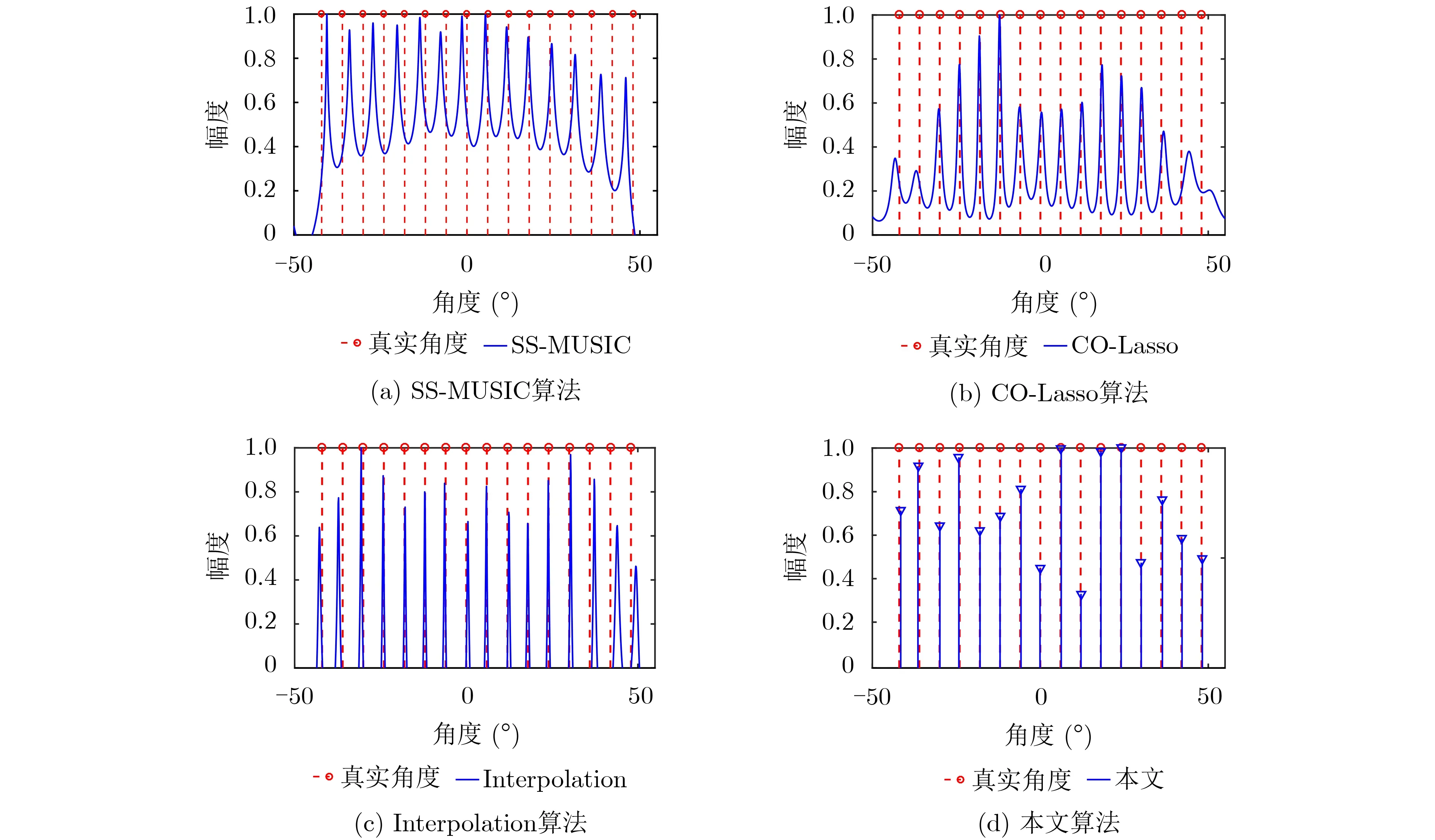
圖2 幅相誤差條件下的歸一化空間譜

4.2 估計精度分析

將本文所提算法的性能與3種非均勻噪聲條件下互質陣列的DOA估計算法進行比較，包括CCVS[18]算法，TVNM[19]算法和CMRCS[20]算法。設有12個均勻分布于-42°～35°方向的遠場窄帶信號。圖3和圖4分別為均方根誤差隨信噪比和快拍數的變化關系。圖3中，設置快拍數為600，信噪比變化范圍為-15～15 dB，進行300次蒙特卡羅實驗。圖4中，設置信噪比SNR為5 dB，快拍數變化范圍為100～700，進行300次蒙特卡羅實驗，快拍數變化對DOA估計均方根誤差的影響。假設非均勻噪聲協方差矩陣Q各對角線元素為[1,10]，在每次實驗中，從[1,30]范圍隨機選擇各對角線元素。

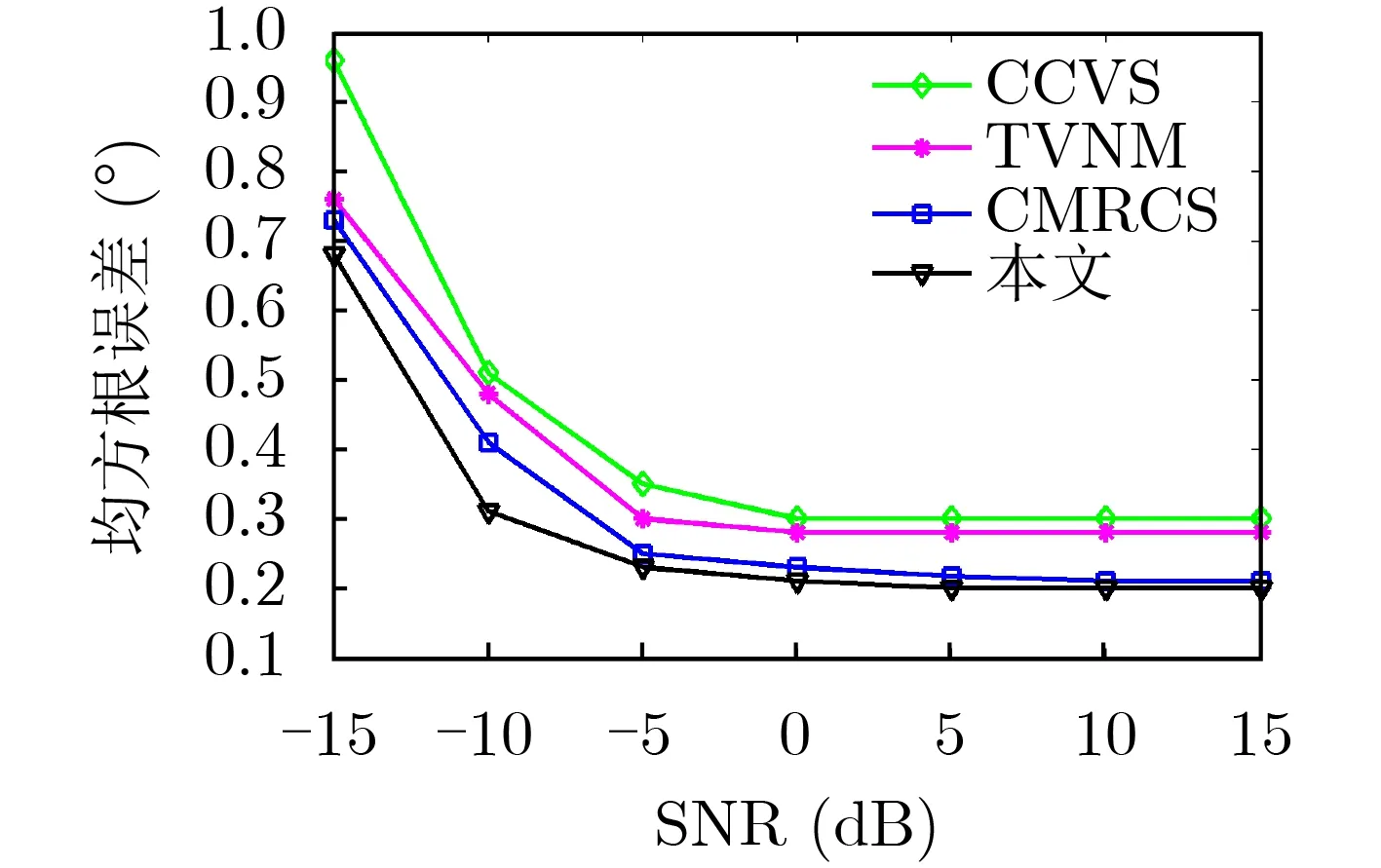
圖3 均方根誤差隨信噪比變化

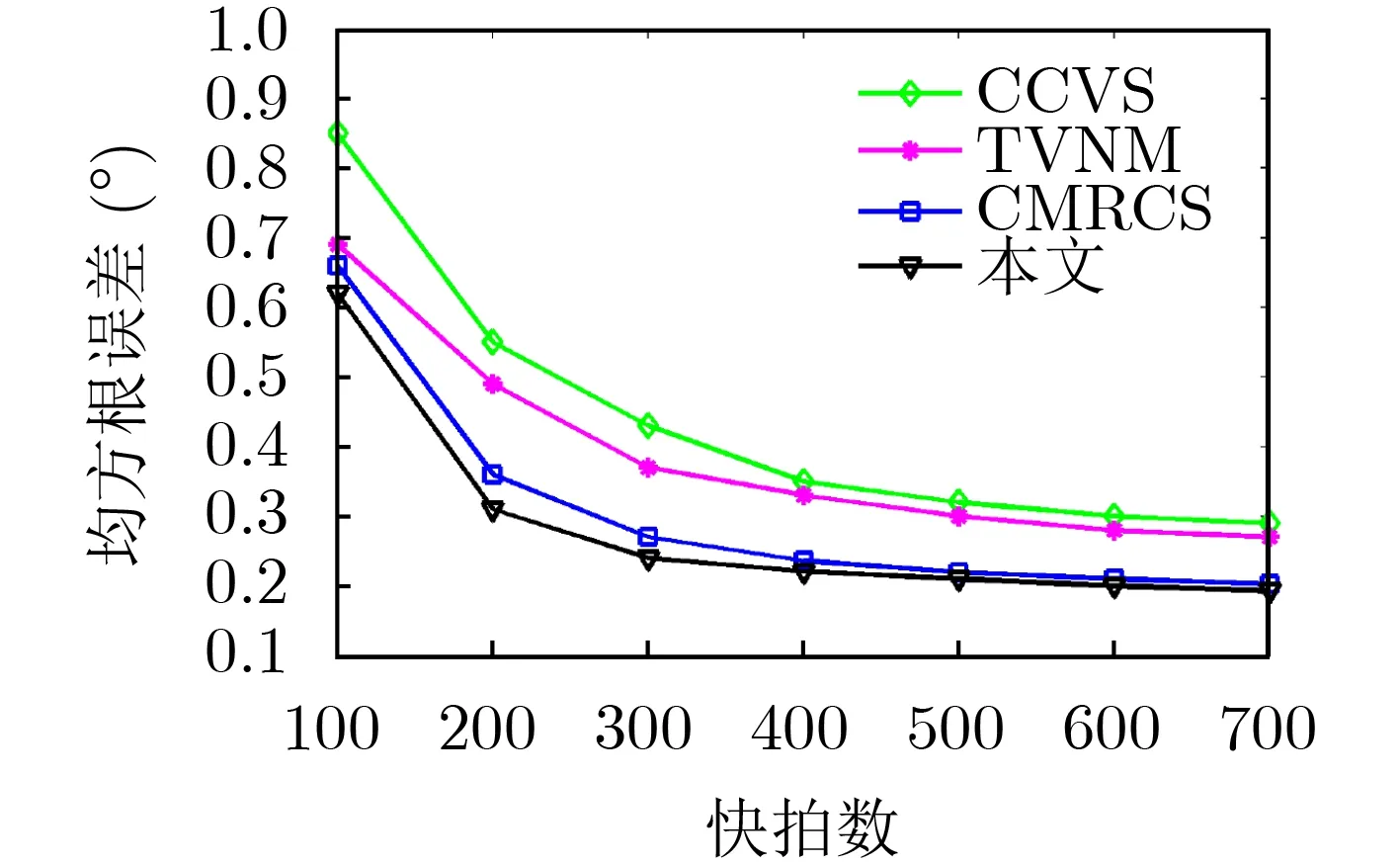
圖4 均方根誤差隨快拍數變化

由圖3和圖4可知，在相同條件下，提高信噪比或增加快拍數，4種算法的角度估計精度均逐步提高，在設置較高信噪比和快拍數情況下，CCVS算法和TVNM算法估計精度明顯低于CMRCS算法和本文算法。這是因為CCVS算法和TVNM算法僅利用了差聯合陣列中連續的虛擬陣元，舍棄了非連續部分，導致損失了部分有用信息；并且，這兩種算法本質上是通過平均協方差矩陣對角線元素來實現噪聲協方差矩陣白化，對噪聲抑制效果有限。CMRCS算法和本文算法均充分利用了所有的虛擬陣元，其中，CMRCS算法通過移除采樣協方差矩陣對角線元素來構造無噪聲協方差矩陣，移除噪聲協方差矩陣對角線元素的同時，也移除了信號協方差矩陣對角線元素，造成了信息損失。本文算法則通過選取對角線元素中的最小值替換其余元素，抑制非均勻噪聲的同時保留了有用信息，因而估計效果更好。

4.3 分辨概率分析

由圖5可知，本文算法角度分辨概率最高，在信噪比增加至0 dB時，本文算法和CMRCS算法角度分辨概率均趨于100%，而CCVS算法和TVNM算法分辨概率相對較低。由圖6可知，在角度間隔增加至1.4°時，本文算法和CMRCS算法分辨概率趨近100%，且本文算法分辨概率最高，相比于CCVS算法和TVNM算法有明顯的分辨優勢。因此，本文算法在不同信噪比和不同角度間隔情況下均具有明顯的高分辨優勢。

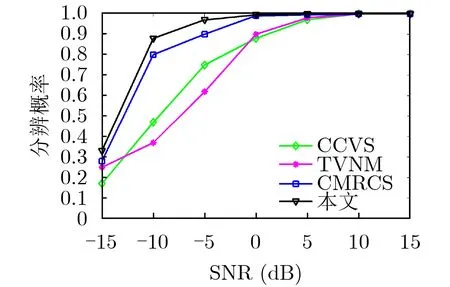
圖5 分辨概率隨信噪比變化

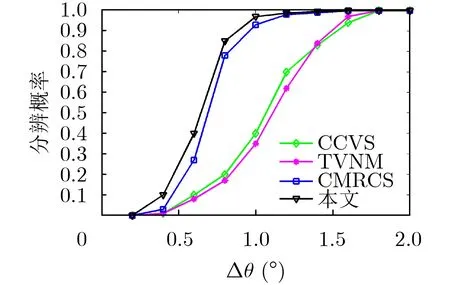
圖6 分辨概率隨角度間隔變化

5 結束語

為了解決互質陣列欠定DOA估計方法在非均勻噪聲條件下性能下降的問題，本文提出一種基于協方差矩陣重構和矩陣填充的DOA估計方法。通過重構接收數據協方差矩陣，有效抑制了非均勻噪聲，并將重構后的協方差矩陣進行擴展和填充，實現欠定DOA估計。理論分析和仿真實驗表明，在非均勻噪聲條件下，該方法保證了互質陣列欠定DOA估計的魯棒性。相對于現有方法，該方法充分利用了所有虛擬陣元，有效抑制非均勻噪聲的同時不丟失有用信息，提高了估計性能。