基于信息熵的靈巧噪聲干擾識別方法*

李杰然

（91404部隊 秦皇島 066200）

1 引言

隨著電子技術的快速發展，雷達與雷達干擾之間的對抗更加激烈。雷達干擾技術迅猛發展，新的干擾樣式不斷涌現。靈巧噪聲干擾是目前研究較為熱點的一種干擾樣式，其特征是兼具噪聲壓制和欺騙干擾的效果。雷達為了有效對抗干擾，首要前提是能夠準確識別干擾樣式。目前，許多國內外專家已經在雷達干擾識別方面做了大量研究工作。文獻［1］以欺騙干擾樣式為研究對象，分析了干擾信號與目標回波信號在頻譜上的差異，提出了一種以雙譜為特征參數的干擾識別方法。文獻［2］以雷達拖引干擾樣式為研究對象，在干擾樣式識別中引入霍夫曼樹和逆云模型。文獻［3］重點研究轉發式欺騙干擾，將擬合優度用于雷達干擾樣式識別。文獻［4］針對欺騙干擾樣式，提出以小波分解干擾信號能量比作為特征的雷達干擾樣式識別方法。文獻［5］以間歇采樣轉發干擾為研究對象，提出了一種基于熵理論的干擾識別方法。文獻［6］以靈巧噪聲干擾為研究對象，提出了一種多維聯合特征的干擾識別方法。隨著雷達干擾技術的不斷發展，雷達干擾樣式將會不斷創新，圍繞靈巧噪聲干擾樣式識別研究也將持續深入。為此，本文以卷積調制、數字多時延和間歇采樣轉發三種靈巧噪聲干擾為研究對象［7］，分析了各干擾信號在頻域上的特征，將信息熵作為識別特征，采用支持向量機方法進行了仿真驗證。當信噪比大于0dB時，干擾識別準確率超過95%。

2 干擾信號分析

不同的雷達發射信號，靈巧噪聲干擾信號也將隨之改變。為了針對性研究，以雷達常用線性調頻信號為例，對三種靈巧噪聲干擾信號進行建模分析。

設s(t)為雷達發射信號，頻譜為S(f)，則

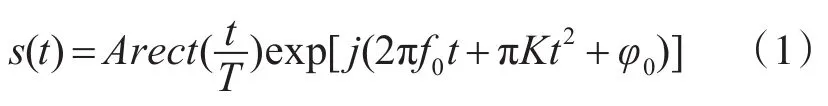
其中，A表示信號幅度；f0表示載波頻率；T表示脈沖寬度；K表示調諧率；φ0表示信號初始相位。

卷積調制干擾信號［7］可以通過將事先設計好的視頻信號與接收到的雷達信號進行卷積形成。假設視頻信號ξ(t)，形成的卷積干擾信號為j1(t)，其頻譜為J1(f)，則

式中?表示卷積。

數字多時延干擾［8～9］是先對接收存儲的雷達發射信號和視頻信號進行數字采樣離散化，再以有限長序列進行卷積所形成的信號。設數字多時延干擾信號為j2(t)，頻譜為J2(f)，則

式中s(t-τn)表示對s(t)的延時。

間歇采樣轉發干擾［10～11］是先對接收的雷達信號進行間歇采樣再按特定方式轉發所形成的信號。假設采用直接轉發方式形成干擾信號，假設采樣信號為矩形脈沖串p(t)，其脈沖寬度為τ，脈沖重復周期為Ts

則，采樣信號為

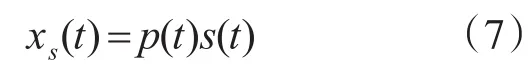
那么，間歇采樣轉發干擾信號j3(t)為

其干擾信號頻譜J3(f)為

在頻域上分析對比雷達發射信號與干擾信號的區別。設采用線性調頻信號作為雷達發射信號，載波頻率為2GHz，脈沖寬度為20μs，調頻帶寬為5MHz，則目標回波信號頻譜如圖1所示。

圖1 目標回波信號頻譜

卷積調制干擾采用均值為0方差為1高斯白噪聲作為視頻信號與雷達信號進行卷積生成，其頻譜如圖2所示。數字多時延干擾設置延遲時間為0.6μs，有限序列數N取30，其頻譜如圖3所示。間歇采樣轉發干擾采用信號周期為2.5μs，占空比為0.4的脈沖采樣信號生成，其頻譜如圖4所示。

圖2 卷積調制干擾信號頻譜

圖3 數字多時延干擾信號頻譜

圖4 間歇采樣轉發干擾信號頻譜

可以看出，干擾信號頻譜與目標回波信號寬度相當。在信號帶寬內，目標信號頻譜幅度變化起伏較小，而干擾信號頻譜幅度變化起伏較大且雜亂混疊。這就為干擾識別的特征選取提供的方向。針對目標信號與干擾信號頻譜幅上的差異，可以通過引入熵理論評價信號的不確定性復雜性，從而識別出干擾信號。

3 特征提取

熵作為熱力學領域的重要參數，是德國物理學家克勞修斯在1865年在研究熱力學第二定律時提出［12～14］。對于物質系統來說，熵可以作為系統雜亂性或無序性的度量。信息熵（又名香農熵）是1948年香農在研究通信系統信息度量問題時提出的，其綜合了概率論和數理統計方法，可以定量的衡量信源的平均不確定度。

設一個由離散隨機變量構成的信號M={m1,m2,...,mn}，其各變量發生的概率為，且有，則信號的信息熵定義為

信息熵可以表征信號狀態分布復雜度。信號的分布狀態越復雜，其信息熵越大。因此，可以將信息熵用于干擾信號的特征識別。

下面給出信息熵特征參數的提取流程：

1）對三種靈巧噪聲干擾與目標回波信號做FFT處理，將信號變換到頻率域；

2）在帶寬內將信號做歸一化處理，去除頻帶外的噪聲影響；

3）對頻譜幅度進行歸一化，求出每一頻點對應的能量，計算每一點能量占總能量的比例，記為

4）按照信息熵的定義求出各信號信息熵。

4 仿真驗證

采取蒙特卡羅方法進行仿真實驗驗證。設雷達采取線性調頻信號，發射載頻為2GHz，頻譜寬度為5MHz，脈沖寬度為20μs。卷積調制干擾采用的視頻信號為高斯白噪聲信號，其均值為0，方差為1；數字多時延干擾信號時延為0.6μs，序列數N為30；間歇采樣轉發干擾采用脈沖采樣信號，其周期為2.5μs，占空比為0.4的；信噪比設置為-5dB到25dB。干信比分別設置為0dB、5dB和10dB，做300次仿真實驗，計算各信號的信息熵均值，結果如圖5～7。

圖5 頻譜信息熵均值（干信比為0dB）

圖6 頻譜信息熵均值（干信比為5dB）

圖7 頻譜信息熵均值（干信比為10dB）

從實驗結果可以看出，一是干擾信號與目標回波信號的頻譜信息熵分離度較大；二是干擾信號頻譜信息熵均值隨信噪比增加逐漸趨于穩定，可應用于干擾信號的特征識別。卷積調制干擾和數字多時延干擾頻譜信息熵與目標回波信號頻譜信息熵穩定值相差較大，隨著干信比的增加，分離度保持較好。但間歇采樣轉發干擾頻譜信息熵與目標回波信號頻譜信息熵穩定值相近，在干信比增大時，會出現信息熵交叉的現象，會影響干擾信號的識別。

下面將信號頻譜信息熵特征作為特征參數，采用支持向量機對干擾信號與目標回波信號進行識別，其分類器設計為徑向基核函數。干信比為10dB，信噪比從-5dB變化到25dB，做300次仿真，選取其中150次數據作為訓練樣本，其余150次數據作為測試樣本，實驗結果如圖8所示。可以看出，當信噪比大于0dB時，三種干擾的識別準確率在95%以上，識別效果較好。但當信噪比小于0dB時，對間隙采樣轉發干擾識別存在低點，這是由于此條件下間歇采樣轉發干擾頻譜信息熵與目標回波信號頻譜信息熵穩定值相近造成的。

圖8 各干擾信號識別準確率（干信比為10dB）

5 結語

本文重點研究了靈巧噪聲干擾識別問題。選取卷積調制、數字多時延和間歇采樣轉發三種靈巧噪聲干擾樣式作為研究對象，分析了其頻譜特性，提出了基于信號頻譜信息熵的干擾識別方法。采用支持向量機方法對干擾信號識別效果進行了仿真驗證。實驗結果表明，在信噪比大于0dB時，干擾信號識別準確率超過95%，識別效果較好。隨著電子技術的不斷進步，雷達干擾將會更加多樣化，需要持續深入開展干擾識別研究。