有限元分割的共軛方向優(yōu)化算法

李有堂，梅鶴齡

（蘭州理工大學(xué)機(jī)電工程學(xué)院，甘肅蘭州 730050）

隨著科技的進(jìn)步和發(fā)展，精密、超精密設(shè)備與加工技術(shù)標(biāo)志著一個國家制造領(lǐng)域的尖端技術(shù)水平，已成為當(dāng)今世界各國進(jìn)行科技競爭的一個重要手段[1]。計算機(jī)的快速發(fā)展以及互聯(lián)網(wǎng)的迅速普及，信息在互聯(lián)網(wǎng)上爆發(fā)式增長，文本、圖像、音頻、視頻等的發(fā)展導(dǎo)致表達(dá)數(shù)據(jù)需要更高的維度[2]。這些改變無疑對數(shù)據(jù)類問題的處理提出了更高的要求，不僅對數(shù)據(jù)的處理效率和便捷度提出了要求，對估算計算的數(shù)值要求有更高的準(zhǔn)確度(誤差降低到滿足要求的范圍內(nèi))。

無約束優(yōu)化算法作為最優(yōu)化方法的基礎(chǔ)，在交通運輸、工農(nóng)業(yè)生產(chǎn)、金融、貿(mào)易等眾多領(lǐng)域有著廣泛應(yīng)用。伴隨著信息技術(shù)的飛速發(fā)展,變量維數(shù)的劇增以及結(jié)構(gòu)復(fù)雜性的增強(qiáng)，能有效求解大規(guī)模無約束優(yōu)化問題的算法顯得尤為重要[3]。在優(yōu)化算法的發(fā)展過程中，1964 年由鮑威爾提出的共軛方向法(Conjugate Direction Method)起到了舉足輕重的作用。共軛方向法可以在有限步數(shù)內(nèi)找到二次函數(shù)的極值點和極值，并且對非二次函數(shù)只要具有連續(xù)二階導(dǎo)數(shù)，也是一種有效的算法[4]。但是，共軛方向法的主要缺點是更換方向后所產(chǎn)生的n個矢量有可能是近似線性相關(guān)的，即這些矢量接近于平行。這樣就會出現(xiàn)維度退化現(xiàn)象，導(dǎo)致只能找到局部最優(yōu)解，有可能使真正的全局最優(yōu)解漏掉[5]。

針對共軛方向法的該缺陷，在實際工程應(yīng)用中通過與其他算法組合或?qū)λ惴ㄟM(jìn)行改進(jìn)以提高解決問題的準(zhǔn)確度[6]。例如：在一些優(yōu)化問題中，當(dāng)粒子群算法(PSO)經(jīng)過一段時間的迭代后，會陷入局部最優(yōu)解的局部極小值中，這時采用共軛方向法，以局部最優(yōu)解作為初始猜測，將高維函數(shù)優(yōu)化問題轉(zhuǎn)化為低維函數(shù)優(yōu)化問題，幫助粒子群算法克服局部極小問題[7]；對于移動機(jī)器人全局路徑規(guī)劃問題，先用共軛方向法搜索局部最優(yōu)解，再用改進(jìn)模擬退火算法(SAA)跳出局部最優(yōu)解，依此更新溫度值，如此反復(fù)操作，直至找到全局最優(yōu)解[8]；針對遺傳模擬退火算法的局部搜索能力不足，并且有可能早熟和遺失最優(yōu)解的問題，提出一種將遺傳模擬退火算法和共軛方向法相結(jié)合的混合遺傳模擬退火算法[9]；還有對多維優(yōu)化問題的求解，通過對Powell 機(jī)械優(yōu)化方法的改進(jìn)，提出了方向組不降維的構(gòu)造共軛方向法[10]。

隨著科技的發(fā)展，基礎(chǔ)科學(xué)也在進(jìn)步，對于不同的優(yōu)化問題采用不同的優(yōu)化算法，一些有約束問題往往采用無約束優(yōu)化算法進(jìn)行求解。通過以上綜合分析，提出了一種求解有約束優(yōu)化問題的有限元分割共軛方向法，可以杜絕所求優(yōu)化解為局部最優(yōu)解的產(chǎn)生。

1 共軛方向法

共軛方向法是利用共軛方向作為搜索方向的無約束極小算法，而且已證明這類算法應(yīng)用于具有正定Hesse 矩陣的二次函數(shù)時，最多n次迭代即可達(dá)到極小點。這類算法具有有限收斂性，形成共軛方向的方法很多，每一種不同的構(gòu)造共軛方向的方法形成一種具體的共軛方向法，因而共軛方向法是一大類算法[4]。

1.1 共軛方向法基本原理

m個n維向量S1,S2,…,Sm，滿足=0，i≠j且A正定，則這m個向量一定是線性無關(guān)的。在n維空間中的任意向量，均可以用n個線性無關(guān)的n維向量表示。

設(shè)目標(biāo)函數(shù)為：

它的極小點為X*，初始點X0,S0,S1,S2,…,Sn-1為關(guān)于A的n個共軛向量，則有：

將式（2）寫成差分格式：

式（3）表明，經(jīng)(k+1)次迭代后，Xk+1→X*,Xk+1為目標(biāo)函數(shù)沿Sk方向的一個極小點。則：

對于二元二次函數(shù)只需進(jìn)行兩次直線搜索就可以求到極小值點。

圖1 二元二次函數(shù)搜索圖

1.2 共軛方向法

共軛方向法具有二次終止性，是一個概念性算法，實現(xiàn)算法的關(guān)鍵在如何選取共軛方向[11]，不同的選取會產(chǎn)生不同的共軛方向法。其通用格式如下：

第一步：任取X0∈Rn,0 ≤ε＜＜1,k=0，計算g0=g(X0)和初始點X0的下降方向d0，s.t.；第二步：求解minf(Xk+αdk),λ≥0，得解αk(即αk是一維搜索的最優(yōu)解)；

第三步：計算αk、Xk+1，使得Xk+1=Xk+αkdk；

第四步：若Xk+1滿足迭代終止準(zhǔn)則‖gk+1‖≤ε，停止迭代，輸出Xk+1；否則，轉(zhuǎn)至第五步；

第五步：根據(jù)共軛方向的構(gòu)造方法獲得搜索方向dk+1，使得dTk+1Gdj=0,j=0,1,…,k。令k=k+1，轉(zhuǎn)至第二步。

共軛方向法的程序流程圖如圖2 所示。

圖2 共軛方向法的程序流程圖

2 有限元分割共軛方向法

許多優(yōu)化算法在理論上是用來解決無約束優(yōu)化問題的，但是在實際工程問題中往往需要解決的是有約束的優(yōu)化問題[12]，所以一些有約束優(yōu)化問題往往采用無約束優(yōu)化算法進(jìn)行求解[13]。針對共軛方向法所求解有可能為局部最優(yōu)解的問題，對共軛方向法加以改進(jìn)，用以求解有約束的優(yōu)化問題。算法執(zhí)行過程如下所示：

第一步：任取X0∈Rn,X0=(x1,x2,…,xn)，若x1∈[a1,b1],x2∈[a2,b2],…,xn∈[an,bn],ai,bi∈R,i=1,2,…,n。將各個維數(shù)的取值區(qū)間進(jìn)行有限分割，按各個維數(shù)的區(qū)間劃分節(jié)點進(jìn)行排列組合。例如：令xi=[ai,b1]∪[c1,c2]∪,…,∪[cm-1,cm]∪[cm,bi]，然后依次取區(qū)間分割節(jié)點ai,c1,c2,…,cm,bi為xi的值，最后將xi的節(jié)點其他xj的節(jié)點依次進(jìn)行排列組合，取得初始點X0,m∈R,i≠j,i=1,2,…n,j=1,2,…n。

第二步：取初始點X0,0 ≤ε＜＜,1,k=0，計 算g0=g(X0)和初始點X0的下降方向d0,s.t.dT0g0＜0；

第三步：求解minf(Xk+αdk),λ≥0，得解αk(即αk是一維搜索的最優(yōu)解)；

第四步：計算αk,Xk+1，使得Xk+1=Xk+αkdk；

第五步：若Xk+1滿足迭代終止準(zhǔn)則‖gk+1‖≤ε，停止迭代，輸出Xk+1，將其保存于極值保存數(shù)組，然后轉(zhuǎn)至第一步選取新的起始點；否則，轉(zhuǎn)至第六步；

第六步：根據(jù)共軛方向的構(gòu)造方法獲得搜索方向dk+1，使得。令k=k+1，轉(zhuǎn)至第三步。

第七步：根據(jù)極值保存數(shù)組所得各個極值中求取最小值點，最后輸出在該約束內(nèi)的全局最優(yōu)解。

有限元分割共軛方向法的程序流程圖如圖3所示。

圖3 有限元分割共軛方向法的程序流程圖

3 目標(biāo)函數(shù)的算例驗證

以求解f(x)最小值為例：

目前多數(shù)優(yōu)化問題的解決依賴于計算機(jī)軟件，如MATLAB 軟件的優(yōu)化工具箱[14]，可用MATLAB 根據(jù)以上兩種算法的執(zhí)行過程進(jìn)行編程，然后用所編程序分別求解以上目標(biāo)函數(shù)的最優(yōu)解。

3.1 共軛方向法的算例驗證

根據(jù)圖2 所介紹的共軛方向法的程序流程圖用MATLAB 進(jìn)行編程，定義精度為0.000 01，計算程序如下：

選取不同初值X0進(jìn)行迭代計算，可以得到不同的極值和極值點，如表1 所示。

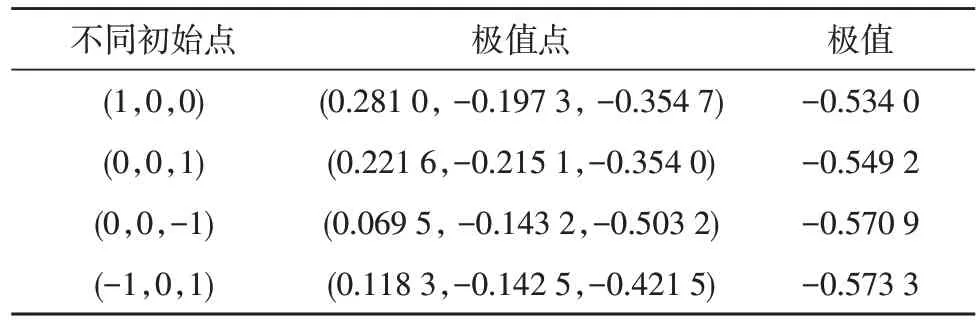
表1 共軛方向法不同初始點迭代結(jié)果

從計算結(jié)果可以看出，雖然定義的精度相同，但是選擇不同的初始點進(jìn)行迭代，所得到的極值點和極值各不相同，并且計算結(jié)果的差距較大。該結(jié)果充分證明了共軛方向法存在的缺點，會陷入局部極值而無法找到全局最優(yōu)點。就科技的發(fā)展而言，計算速度已不是問題，最主要的問題是計算結(jié)果的準(zhǔn)確度，這就意味著需要更優(yōu)的計算方法解決準(zhǔn)確度問題[15]。

3.2 有限元分割共軛方向法的算例驗證

根據(jù)圖3 的有限元分割共軛方向法的程序流程圖進(jìn)行MATLAB 編程，定義精度也為0.000 01，并設(shè)置預(yù)期極值為0(所設(shè)預(yù)期極值應(yīng)大于最終計算極值，如果所設(shè)預(yù)期極值不大于計算極值，計算結(jié)果將會是設(shè)置的預(yù)期結(jié)果，需重新設(shè)置預(yù)期極值進(jìn)行重新計算)，計算程序如下：

令初始點X0=(x1,x2,x3)，由題知x1,x2,x3∈[-1,1]，設(shè)每個分割單元的長度均相等，分割單元長度為0.1，則x1、x2、x3的分割節(jié)點可取為-1,-0.9,…,0.9,1。將所設(shè)參數(shù)代入所編程序中進(jìn)行迭代計算，可以得到最終的極值和極值點，如表2 所示。

表2 有限元分割共軛方向法迭代結(jié)果

由表2 所得極值與表1 所得極值進(jìn)行對比，可以得出表2 所得極值小于表1 所有極值。這說明有限元分割共軛方向法的迭代結(jié)果優(yōu)于共軛方向法，并且可以避免在求解過程中陷入局部最優(yōu)解的缺點。通過編程驗證可知，當(dāng)有限元分割共軛方向法的分割單元長度越小，則所得解越優(yōu)，就當(dāng)今科技發(fā)展的程度，計算速度已不是問題[16]，所以該優(yōu)化計算算法具有很大的實際應(yīng)用價值。

4 結(jié)論

該文在共軛方向法的基礎(chǔ)上提出了有限分割的共軛方向法，并通過MATLAB 編程對兩種算法的尋優(yōu)結(jié)果進(jìn)行對比，可得出的主要結(jié)論如下：

1）提出的有限元分割共軛方向法的迭代結(jié)果優(yōu)于共軛方向法，并且可以避免在求解過程中陷入局部最優(yōu)解的缺點。

2）有限元分割共軛方向法具有可移植性，可以根據(jù)不同的問題可以進(jìn)行不同參數(shù)設(shè)置，可以作為求解大規(guī)模優(yōu)化問題的主要方法。

3）有限元分割共軛方向法克服了最速下降法的慢收斂性，并且保留了共軛方向法的優(yōu)點，具有二次終止性。

4）有限元分割共軛方向法具有簡單、易于編程、需要的儲存空間小等優(yōu)點。

5）有限元分割共軛方向法不受維度限制，可以用于多維問題的求解。

6）當(dāng)有限元分割共軛方向法的分割單元長度越小，則所求解越優(yōu)。