基于純方位的多無人機(jī)協(xié)同目標(biāo)跟蹤算法

辛沙歐，陳可，宋震林，桂欣穎，戚國(guó)慶

（南京理工大學(xué)自動(dòng)化學(xué)院，江蘇南京 210094）

近年來，無人機(jī)技術(shù)發(fā)展迅猛，廣泛應(yīng)用于各領(lǐng)域之中。隨著電子對(duì)抗技術(shù)在現(xiàn)代戰(zhàn)爭(zhēng)中的地位越來越高，通過獲取目標(biāo)的方位、多普勒變化率、到達(dá)時(shí)間等信息確定目標(biāo)位置的無源定位研究逐漸吸引了更多的關(guān)注[1]。由于成本和重量的限制，無源純方位傳感器被廣泛應(yīng)用于被動(dòng)跟蹤中的無源定位。例如，分布式控制及定位中的純方位跟蹤[2]、包圍控制中的方位或相對(duì)視距觀測(cè)[3]、無人機(jī)編隊(duì)飛行的視覺導(dǎo)航與跟蹤[4]。純方位跟蹤系統(tǒng)是對(duì)目標(biāo)進(jìn)行連續(xù)觀測(cè)，積累測(cè)角信息，從而獲得目標(biāo)狀態(tài)的精確估計(jì)，包括目標(biāo)的位置和速度，從而控制觀測(cè)器進(jìn)行跟蹤[5]。多站無源組網(wǎng)定位技術(shù)作為更加有效的無源定位方法，己經(jīng)受到國(guó)內(nèi)外科研人員的高度重視[6]。

針對(duì)純方位目標(biāo)跟蹤問題，文獻(xiàn)[7-9]討論了純方位下的目標(biāo)估計(jì)策略，其中文獻(xiàn)[9]在文獻(xiàn)[7]中的估計(jì)器基礎(chǔ)上加入卡爾曼濾波，得到目標(biāo)狀態(tài)的無偏估計(jì)，進(jìn)一步改善了目標(biāo)估計(jì)的精度，為運(yùn)動(dòng)目標(biāo)被動(dòng)跟蹤提供了更多的可能。

隨著任務(wù)和應(yīng)用的日益復(fù)雜，多無人機(jī)協(xié)同跟蹤問題越來越受到重視。常見的是研究一組移動(dòng)智能體對(duì)未知目標(biāo)的定位和繞航問題，目的是使智能體以期望的半徑圍繞目標(biāo)旋轉(zhuǎn)，并在目標(biāo)周圍形成均勻的隊(duì)形[10-13]。Liya Dou 等[11]研究了一組移動(dòng)智能體基于純方位測(cè)量對(duì)靜止或者移動(dòng)目標(biāo)的定位和包圍問題，在文獻(xiàn)[7]的估計(jì)器基礎(chǔ)上，設(shè)計(jì)了分布式控制率，保證智能體群分別在目標(biāo)或其鄰域周圍全局收斂到一個(gè)精確的均勻圓形，估計(jì)誤差和控制誤差可以收斂到零的鄰域。針對(duì)未知目標(biāo)，J.Shao 以及R.Li 在不同維度研究了定位與環(huán)航問題[14-15]。

現(xiàn)有的純方位量測(cè)下多無人機(jī)協(xié)同目標(biāo)定位與跟蹤的估計(jì)誤差和控制誤差只能收斂到零的鄰域，而不能收斂到零，尤其是對(duì)于快速移動(dòng)的目標(biāo)。因此，針對(duì)快速移動(dòng)的目標(biāo)，如何提高目標(biāo)估計(jì)精度和減小控制誤差還有待進(jìn)一步研究。

該文研究了多無人機(jī)在二維環(huán)境下圍繞一個(gè)位置未知的運(yùn)動(dòng)目標(biāo)的控制器設(shè)計(jì)，以及僅利用方位測(cè)量信息的精確目標(biāo)狀態(tài)估計(jì)器的設(shè)計(jì)問題。針對(duì)文獻(xiàn)[7]中的估計(jì)器方法，提出了結(jié)合卡爾曼濾波的方式，以獲得更加精確的目標(biāo)狀態(tài)。結(jié)果表明，相較于沒有濾波的作用，對(duì)于運(yùn)動(dòng)目標(biāo)的估計(jì)誤差收斂到零，而不是零的鄰域。針對(duì)文獻(xiàn)[11]中的控制器設(shè)計(jì)問題，通過引入虛擬交叉算法，加入目標(biāo)估計(jì)速度項(xiàng)對(duì)原有的控制器進(jìn)行改進(jìn)，可以保證控制誤差收斂到零。最后，仿真結(jié)果驗(yàn)證了文中所提出的估計(jì)器以及控制律的優(yōu)越性。

1 預(yù)備知識(shí)與問題描述

1.1 圖 論

多無人機(jī)系統(tǒng)中N個(gè)無人機(jī)之間的通信情況可以采用無向圖G={V,E} 進(jìn)行描述，其中V={1,2,???,N}為無向圖節(jié)點(diǎn)的集合，E?V×V為無向圖的邊集。A=[aij]∈RN×N是加權(quán)鄰接矩陣，當(dāng)(i,j)∈E，aij=aji=1，(i,j)?E時(shí)，aij=0。假設(shè)該圖沒有自循環(huán)，則aii=0 。節(jié)點(diǎn)i的所有鄰域集合用Ni={j∈V:(i,j)∈E}表示。定義圖G的拉普拉斯矩陣為L(zhǎng)=[lij]∈RN×N,當(dāng)i≠j時(shí)，lij=-aij，。在圖G中由節(jié)點(diǎn)i到節(jié)點(diǎn)j的路徑是以節(jié)點(diǎn)i為起點(diǎn)，以節(jié)點(diǎn)j為終點(diǎn)的一系列不同邊的組合。如果圖G的每一對(duì)不同的節(jié)點(diǎn)都有一條路徑，則圖G是連通的。每個(gè)索引i都是對(duì)N求余得到的，例如，索引N+1 與1 等價(jià)[16]。

1.2 問題描述

首先，假設(shè)無人機(jī)可以在固定的高度飛行，因此只關(guān)注無人機(jī)在二維笛卡爾坐標(biāo)系下的目標(biāo)估計(jì)與定位。無人機(jī)與目標(biāo)在二維平面下的相對(duì)位置如圖1 所示。目標(biāo)及其估計(jì)位置用“+”表示，無人機(jī)的位置用“●”表示。

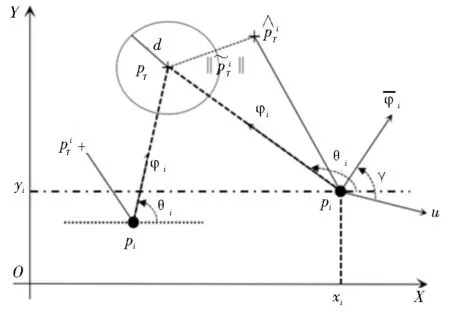
圖1 無人機(jī)與目標(biāo)相對(duì)位置圖形化視圖

考慮一個(gè)在時(shí)間t內(nèi)具有未知軌跡pT(t)=[xT(t),yT(t)]T∈R2的運(yùn)動(dòng)目標(biāo)，和N個(gè)具有已知軌跡pi(t)=[xi(t),yi(t)]T∈R2的無人機(jī)，其中i∈V。假設(shè)每個(gè)無人機(jī)的運(yùn)動(dòng)服從單積分模型：

其中，ui(t)表示無人機(jī)i的控制輸入。

無人機(jī)i對(duì)目標(biāo)的估計(jì)位置可以表示為。無人機(jī)i對(duì)目標(biāo)的觀測(cè)角為θi(t)∈[0,2π)，與目標(biāo)相對(duì)距離用表示，無人機(jī)i與對(duì)目標(biāo)的估計(jì)位置的距離為，無人機(jī)i對(duì)目標(biāo)的估計(jì)誤差為。d為無人機(jī)與目標(biāo)期望間距，即期望環(huán)航旋轉(zhuǎn)半徑。用φi(t)∈R2表示無人機(jī)i指向目標(biāo)的單位方向向量，則：

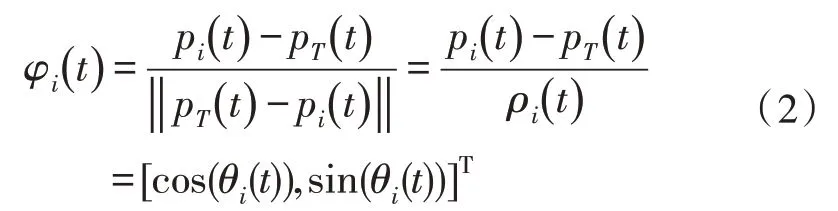
(t)∈R2是φi(t)繞pi(t)順時(shí)針旋轉(zhuǎn)π/2 得到的垂直于φi(t)的單位向量。為了方便起見，假設(shè)逆時(shí)針旋轉(zhuǎn)方向?yàn)檎Ｒ虼耍瑹o人機(jī)i到無人機(jī)j的分離角(i＜j)是通過從無人機(jī)i到目標(biāo)的射線逆時(shí)針旋轉(zhuǎn)直到遇見無人機(jī)j到目標(biāo)的射線：

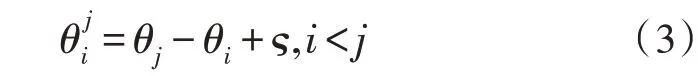
為了設(shè)計(jì)一個(gè)分布式定位方案，利用純方位測(cè)量值來估計(jì)目標(biāo)的未知位置pT(t)，然后設(shè)計(jì)基于局部測(cè)量的分布式控制律，從而實(shí)現(xiàn)以下目標(biāo)：

①估計(jì)誤差收斂到0，即：

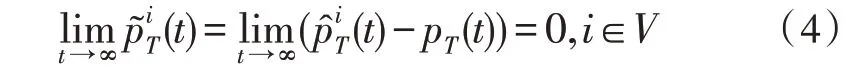
②無人機(jī)i與目標(biāo)之間的距離收斂到指定的相同環(huán)航半徑，即：

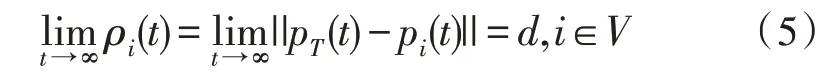
③一組無人機(jī)按照等角均勻分布在以目標(biāo)為中心的指定半徑的圓周上，即：

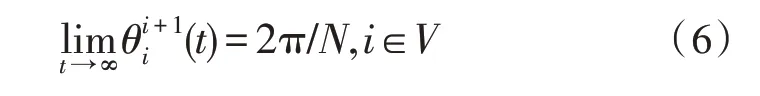
該文主要工作是基于以下假設(shè)進(jìn)行實(shí)現(xiàn)的：

假設(shè)1：存在正常數(shù)u0使得對(duì)于t＞0 時(shí)，且保證任一無人機(jī)i的速度滿足。

假設(shè)2：通信拓?fù)銰是無向連通的。

假設(shè)3：所選擇的pi(0)、pT(0)以及(0)能夠使得ρi(0)、是有限的。

2 算法設(shè)計(jì)

已知多無人機(jī)跟蹤位置未知的移動(dòng)目標(biāo)是一個(gè)估計(jì)和控制的綜合問題，因此這一部分，嘗試同時(shí)為每個(gè)無人機(jī)構(gòu)造估計(jì)器和控制器[17-19]。

為了定位未知目標(biāo)，首先為每個(gè)無人機(jī)提出如下協(xié)作的估計(jì)器：

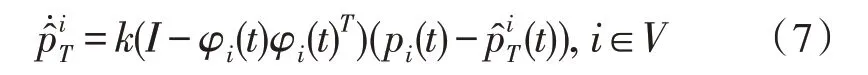
其中，k是正常數(shù)，φi(t)φi(t)T是向量φi(t) 的投影矩陣。目標(biāo)與無人機(jī)之間的幾何位置關(guān)系如圖2所示。

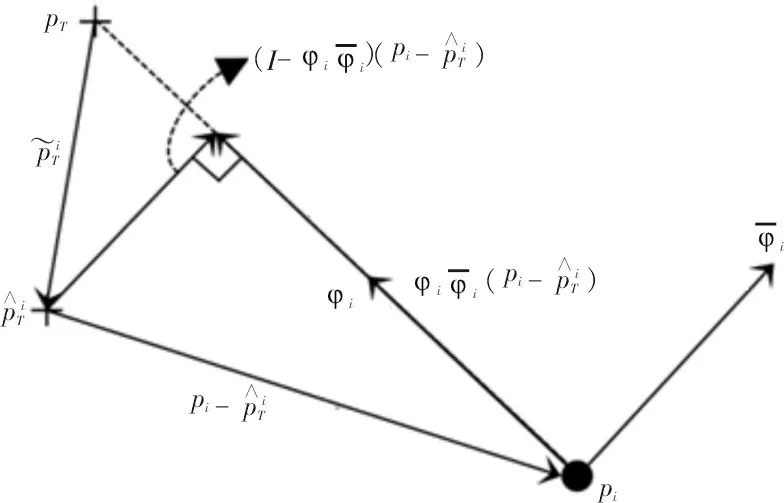
圖2 無人機(jī)與目標(biāo)之間的幾何位置關(guān)系圖

然后，基于無人機(jī)對(duì)目標(biāo)的估計(jì)位置以及鄰居節(jié)點(diǎn)的角度測(cè)量信息為每個(gè)無人機(jī)設(shè)計(jì)如下控制器：

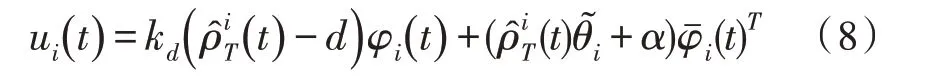
其 中，kd、α是設(shè)計(jì)參數(shù)，分離角誤差。

例如，當(dāng)N=5 時(shí)，期望無人機(jī)能夠在以目標(biāo)為中心的具有指定半徑的圓周上形成如圖3 所示的等角編隊(duì)。

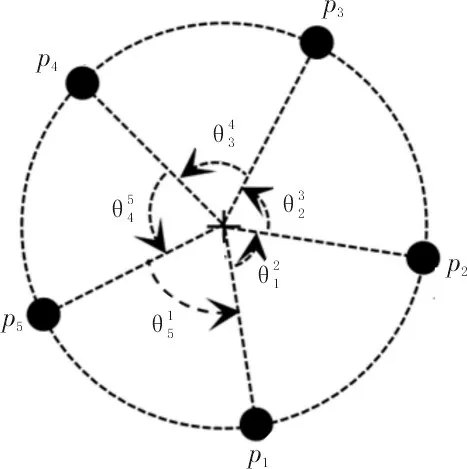
圖3 5個(gè)無人機(jī)期望隊(duì)形示意圖

控制輸入ui(t) 由兩部分組成。徑向項(xiàng)-d)φi(t) 控制無人機(jī)移動(dòng)到指定的環(huán)航跟蹤半徑的圓周上，切向項(xiàng)則保證各個(gè)無人機(jī)之間按照指定的角度分布在以目標(biāo)為中心的圓周上。另外，因?yàn)榍邢蝽?xiàng)依賴于各個(gè)無人機(jī)的期望距離，因此當(dāng)目標(biāo)期望距離較小時(shí)，可以避免過高的角速度。

引理3.1[9]:在基于虛擬交叉算法[14]的式（7）估計(jì)器下，卡爾曼濾波得到的估計(jì)誤差，在t→∞時(shí)是漸近無偏的。其中。

引理3.2[11]:假設(shè)目標(biāo)是靜止?fàn)顟B(tài)，在式（7）估計(jì)器和式（8）控制器下，一組無人機(jī)將收斂于以目標(biāo)為圓心，半徑為d的圓周上，即當(dāng)t→∞時(shí)，ρi(t)→d。

引理3.3[11]:假設(shè)目標(biāo)是靜止?fàn)顟B(tài)，在式（7）估計(jì)器和式（8）控制器下，如果無向拓?fù)銰是樹結(jié)構(gòu)，則一組無人機(jī)將按照指定分離角度分布在以目標(biāo)為中心的具有指定半徑的圓周上，對(duì)于i∈V，當(dāng)t→∞時(shí)，滿足=2π/N。

3 穩(wěn)定性分析

根據(jù)引理5[11]，對(duì)于一個(gè)運(yùn)動(dòng)的目標(biāo)，在式（7）估計(jì)器和式（8）控制器下，無人機(jī)i與目標(biāo)的相對(duì)距離的控制誤差收斂到一個(gè)半徑有限的區(qū)域，但不是收斂到零。因此，提出下列控制器：

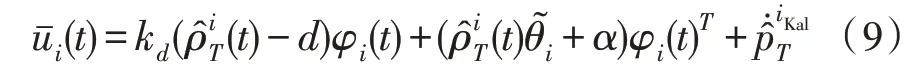
推論1：對(duì)于運(yùn)動(dòng)目標(biāo)，式（9）控制器下無人機(jī)i的環(huán)航跟蹤半徑控制誤差-d一致收斂到零。

證明：定義圖1 所示的笛卡爾坐標(biāo)系為C1，定義以目標(biāo)pT(t) 為原點(diǎn)的參考坐標(biāo)系為C2。則無人機(jī)在C2 坐標(biāo)系下的相對(duì)于目標(biāo)的運(yùn)動(dòng)速度可以描述為：

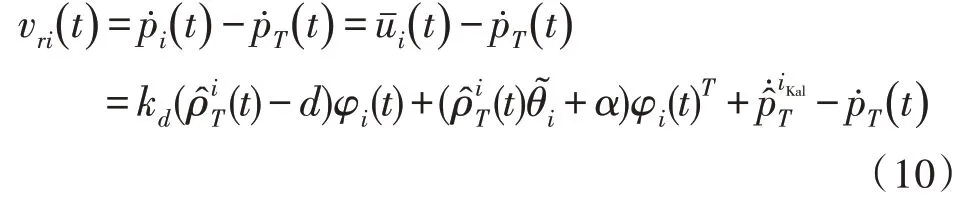
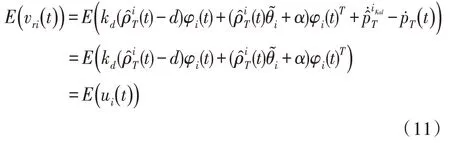
因此，原來的環(huán)航編隊(duì)控制問題可以轉(zhuǎn)化為C2坐標(biāo)系下一組無人機(jī)環(huán)航跟蹤靜止目標(biāo)，根據(jù)引理3.2，一組無人機(jī)將收斂于以目標(biāo)為圓心，半徑為d的圓周上，即當(dāng)t→∞時(shí)ρi(t)→d。證畢。

推論2：對(duì)于運(yùn)動(dòng)目標(biāo)，在式（9）控制器下，如果無向拓?fù)銰是樹結(jié)構(gòu)，則一組無人機(jī)將按照指定分離角度分布在以目標(biāo)為中心的圓周上，對(duì)于i∈V，當(dāng)t→∞時(shí)，滿足=2π/N。

證明：基于推論1 的證明，在C2 坐標(biāo)系下一組無人機(jī)環(huán)航跟蹤靜止目標(biāo)的問題，可以根據(jù)引理3.3，使得無人機(jī)之間的分離角按照2π/n分布在指定半徑的圓周上。

4 仿真驗(yàn)證

4.1 動(dòng)力學(xué)模型選擇

為了能夠得到目標(biāo)更精確的估計(jì)位置，參考文獻(xiàn)[9]在式（7）估計(jì)器引入卡爾曼濾波。首先，選擇目標(biāo)動(dòng)力學(xué)模型相關(guān)參數(shù)為：

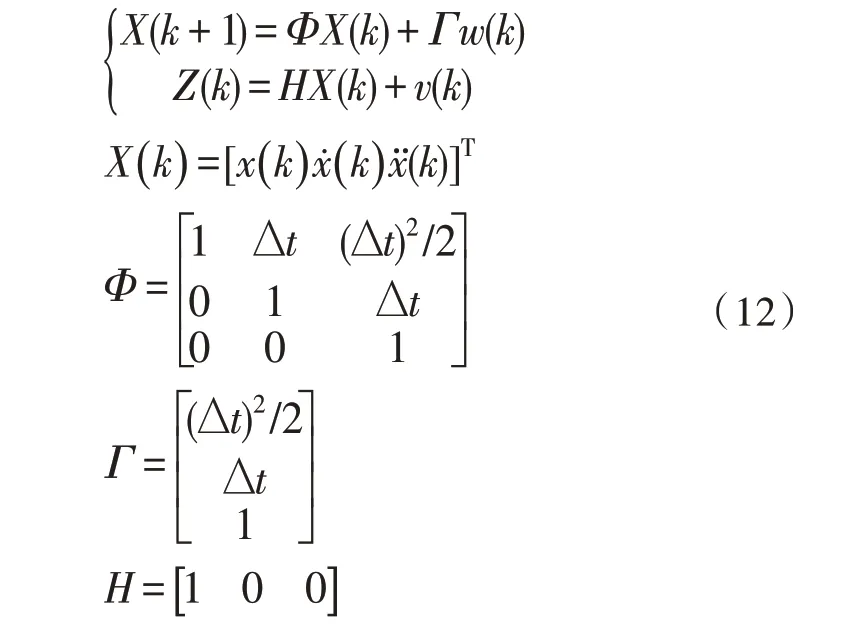
其中，采樣時(shí)間Δt=0.1 s,x、、分別是估計(jì)目標(biāo)的位置、速度以及加速度。假設(shè)模型噪聲w(k)和外界干擾v(k)是均值，且為0，方差分別為的高斯白噪聲，δ(k,l)是狄利克雷函數(shù)，q=0.2,R=0.2。

4.2 低速目標(biāo)仿真對(duì)比

低速目標(biāo)以文獻(xiàn)[11]中的目標(biāo)軌跡vT(t)=[0.2,0.1(cos(0.3t)+1)]T為例，在該文引入卡爾曼濾波的式（7）估計(jì)器和式（9）控制器下，選擇參數(shù)k=5,kd=1,α=0.5 時(shí)，環(huán)航半徑d=10，無人機(jī)初始位置任意，軌跡圖如圖4(a)所示，估計(jì)誤差、收斂半徑以及分離角情況如圖4(b)、(c)、(d)所示。

通過圖4 可以看出，添加濾波以及補(bǔ)償項(xiàng)的控制策略，能夠有效地使一組無人機(jī)在以目標(biāo)為中心且具有指定半徑的圓周上形成等角編隊(duì)。將該次仿真結(jié)果與相同參數(shù)條件下的文獻(xiàn)[11]中的估計(jì)控制策略進(jìn)行比較，以無人機(jī)1 的估計(jì)誤差、收斂半徑以及分離角的收斂情況為例,結(jié)果如圖5 所示。

圖4 低速目標(biāo)在濾波控制策略下的仿真結(jié)果圖

由圖5可以看出加入濾波后的估計(jì)策略收斂速度更快且能夠全局漸近收斂到指定位置，控制誤差更小。

圖5 低速目標(biāo)兩種方法結(jié)果對(duì)比圖

4.3 快速目標(biāo)仿真對(duì)比

快速目標(biāo)以文獻(xiàn)[7]中的目標(biāo)軌跡vT(t)=[1,cos(0.1t)+1)]T為例，在相同動(dòng)力學(xué)模型下，引入濾波方法。在式（7）估計(jì)器與式（9）控制器的作用下，選擇參數(shù)k=5,kd=1,α=0.5 時(shí)，環(huán)航半徑d=8，無人機(jī)初始位置任意，軌跡圖如圖6(a)所示，估計(jì)誤差、收斂半徑以及分離角情況如圖6(b)、(c)、(d)所示。

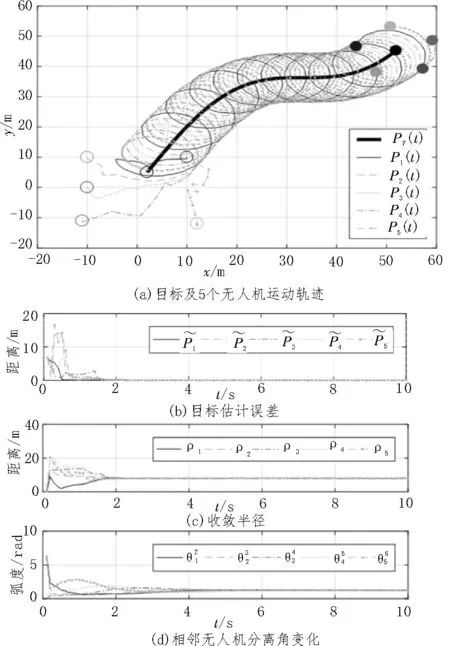
圖6 快速目標(biāo)在濾波控制策略下的仿真結(jié)果圖

通過圖6 可知，添加濾波以及補(bǔ)償項(xiàng)的控制策略針對(duì)高速目標(biāo)也有良好的跟蹤性能。通過兩組仿真結(jié)果對(duì)比可知，在目標(biāo)速度加快且估計(jì)策略相同的情況下，引入濾波的方式所得到的估計(jì)誤差顯著減小，半徑收斂誤差減小，分離角也收斂到2π/5，如圖7所示。

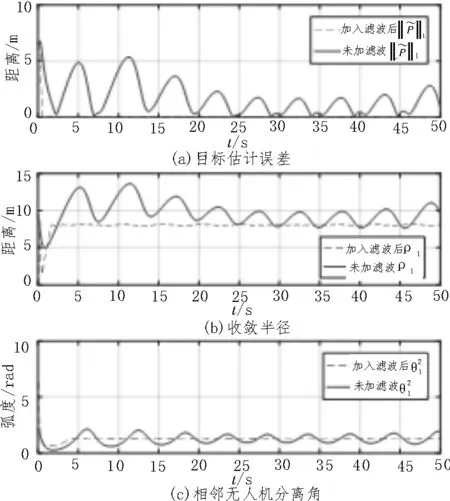
圖7 快速目標(biāo)兩種方法結(jié)果對(duì)比圖

5 結(jié)論

該文主要研究了純方位量測(cè)下多無人機(jī)協(xié)同目標(biāo)跟蹤問題，討論了一種具有無偏估計(jì)誤差的卡爾曼濾波器在多無人機(jī)協(xié)同跟蹤中的應(yīng)用，基于虛擬交叉定位算法對(duì)現(xiàn)有控制律加入估計(jì)目標(biāo)速度進(jìn)行改進(jìn)，保證多無人機(jī)在目標(biāo)周圍形成以目標(biāo)為中心具有指定半徑的等角圓形編隊(duì)。與現(xiàn)有的純方位量測(cè)下多無人機(jī)協(xié)同跟蹤方法進(jìn)行了比較，仿真結(jié)果表明，不管是低速還是快速目標(biāo)，所提出的算法能顯著提高目標(biāo)狀態(tài)估計(jì)的精度，并減小了控制誤差。