一種基于步長指數(shù)遞減策略的果蠅優(yōu)化算法

秋興國，黃潤青

（西安科技大學計算機科學與技術(shù)學院，陜西西安 710054）

果蠅優(yōu)化算法是潘文超[1]于2011 年提出的一種新型演化式群體優(yōu)化算法[2]，該算法模型的構(gòu)建是基于果蠅覓食行為的仿生學原理[3]，目的是尋找全局最優(yōu)值，與其他算法相比具有參數(shù)少、易于實現(xiàn)和局部搜索能力強[4]等優(yōu)點，但它同時具有收斂速度慢、不夠穩(wěn)定、易陷入局部最優(yōu)等局限性[5]。為提高傳統(tǒng)果蠅算法的性能，文獻[6]提出了一種融合變異機制的果蠅優(yōu)化算法，通過使位于種群中心的個體進行變異操作來避免算法易陷入局部極優(yōu)值的情況；文獻[7]提出的果蠅優(yōu)化算法融合了模擬退火的思想，使用非均勻變異的思想優(yōu)化果蠅迭代步長，使算法收斂速度和精度得到了提高；文獻[8]將萊維飛行和反向?qū)W習引入果蠅算法中，通過對果蠅個體進行位置更新來控制算法的收斂速度和精度。

文中提出一種基于t分布及自適應步長策略的果蠅優(yōu)化算法(TEFOA)，該算法從種群位置初始化、果蠅位置更新兩個方面來進行優(yōu)化。通過t分布對果蠅位置更新時進行位置擾動，使種群具有更加隨機的特點，引入指數(shù)遞減步長調(diào)整因子，優(yōu)化了原有算法的位置更新方式。對5 個經(jīng)典性能函數(shù)進行仿真測試，結(jié)果表明，提出的果蠅優(yōu)化算法有較好的收斂速度收斂精度，降低了算法陷入局部極值的可能性。

1 果蠅算法基本介紹

果蠅優(yōu)化算法是一種演化式群智能優(yōu)化算法，是基于果蠅覓食行為提出的。果蠅在嗅覺和視覺[9]上的敏感性優(yōu)于其他物種。在覓食過程中，每個果蠅個體攜帶有食物味道濃度，在算法中將果蠅個體與原點位置距離的倒數(shù)作為味道濃度判定的方法[10]，果蠅群體中所有個體朝味道濃度最優(yōu)的果蠅個體位置飛去[11]，該味道濃度最優(yōu)的果蠅個體位置作為下一次迭代尋優(yōu)過程中果蠅種群的初始位置，通過數(shù)次迭代，不斷更新果蠅群體的最優(yōu)位置，直到得出最優(yōu)解或達到最大迭代次數(shù)[12]。圖1 顯示了果蠅搜尋食物的邏輯迭代過程。

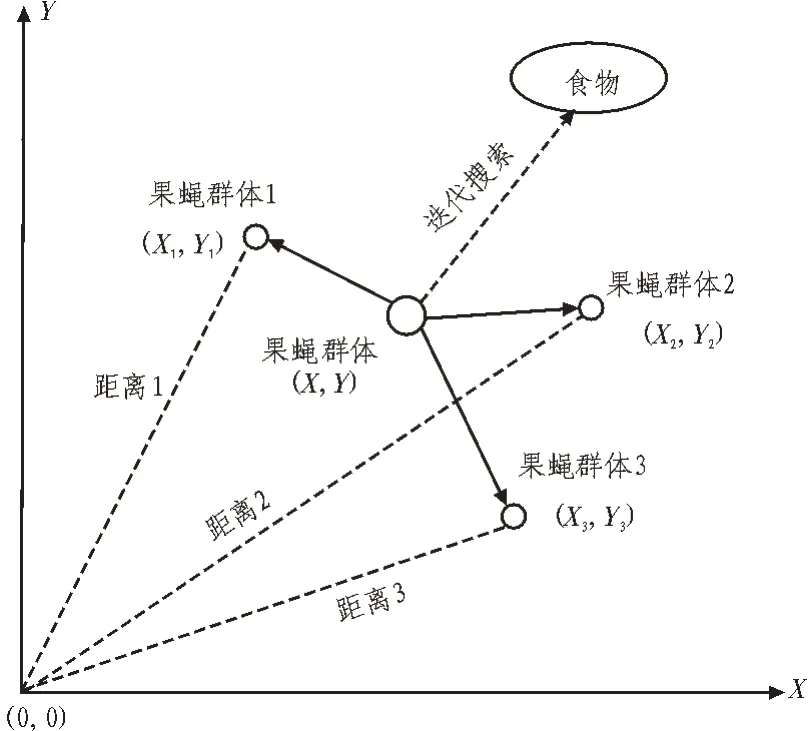
圖1 果蠅群體進化圖

根據(jù)果蠅覓食過程中的行為特點，將標準的果蠅優(yōu)化算法歸納為以下步驟[13]：

1）初始化相關(guān)參數(shù)，主要包括果蠅種群規(guī)模(Sizepop)、群體最大迭代次數(shù)(Maxgen)、果蠅個體初始位置X-axis、Y-axis，并進行群體位置初始化，其中rand()表示[0,1]間的隨機數(shù)。

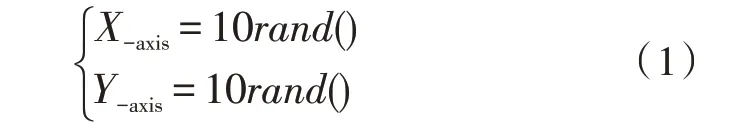
2）確定初始果蠅群體中果蠅個體位置和方向。RValue為果蠅隨機搜索距離和方向的隨機數(shù)。

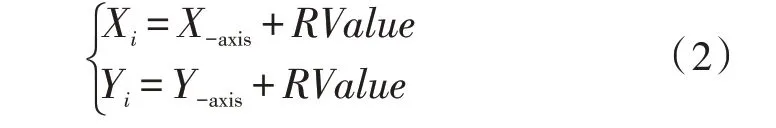
3）利用每個果蠅個體位置坐標與原點的距離Di來計算其味道濃度判定值Si，Si為距離Di的倒數(shù)。

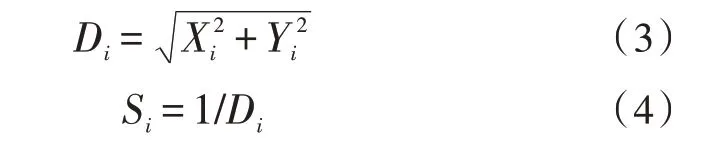
4）將味道濃度判定值Si代入適應度函數(shù)判定函數(shù)[14](或稱為適應度函數(shù)，F(xiàn)itness function)，該函數(shù)是為了計算該種群中果蠅個體的味道濃度Smell(i)。

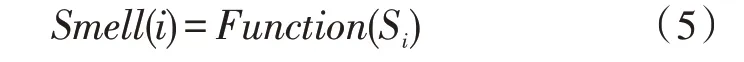
5）找出種群當前味道濃度最優(yōu)的果蠅個體位置，記錄其坐標和味道濃度值。

6）記錄最優(yōu)味道濃度值及對應的橫縱坐標，此時群體果蠅根據(jù)視覺向最優(yōu)個體位置飛去，形成新的果蠅群體。

7）迭代尋優(yōu)階段，重復執(zhí)行步驟2)～步驟5)，判斷當前迭代次數(shù)是否小于最大迭代次數(shù)，當前味道濃度是否優(yōu)于所記錄的最優(yōu)味道濃度，若成立，執(zhí)行步驟6)。

2 改進的FOA算法(TEFOA)

2.1 指數(shù)遞減步長

搜索步長是決定FOA 算法搜索能力的關(guān)鍵因素。由指數(shù)函數(shù)確定的自適應步長在初期迭代搜索時，可在較大范圍內(nèi)展開全局搜索，這有利于跳出局部最優(yōu)解[15]，加快算法的收斂速度，降低運行時間；隨著迭代次數(shù)的增加，在算法運行后期，由于已經(jīng)步入了有潛力的搜索區(qū)域，只需要在區(qū)域內(nèi)進行局部搜索，即設置較小的搜索步長在當前搜索區(qū)域進行精細搜索[16]。受文獻[9]的啟發(fā)，用指數(shù)遞減策略對果蠅算法進行優(yōu)化。所使用的指數(shù)遞減策略表達式為：

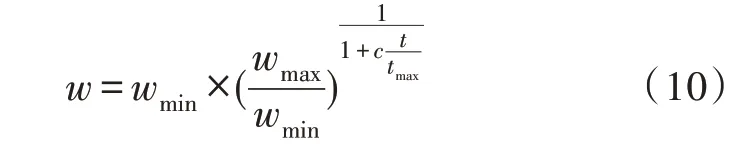
其中，wmax、wmin分別表示w的最大值和最小值，取wmax=1，wmin=0.4[13]；t表示當前迭代次數(shù)；tmax為最大迭代次數(shù)；參數(shù)c取值與文獻[9]保持一致，即c=10。該函數(shù)圖像如圖2 所示，在果蠅算法迭代尋優(yōu)初期，w隨迭代次數(shù)的增加以較快的速率下降，可使果蠅個體在初期能夠保持一個較大的搜索步長。該算法搜索能力較強，為避免出現(xiàn)算法陷入局部極優(yōu)值的情況[17]。在算法迭代尋優(yōu)后期，當?shù)螖?shù)逐漸增加時，w以非線性的動態(tài)逐步減小，搜索步長變小，可以進行精細搜索。這不僅能夠避免因步長較大而跳過最優(yōu)解的可能性[18]，而且還提高了算法后期的收斂精度和時間效率[19]。

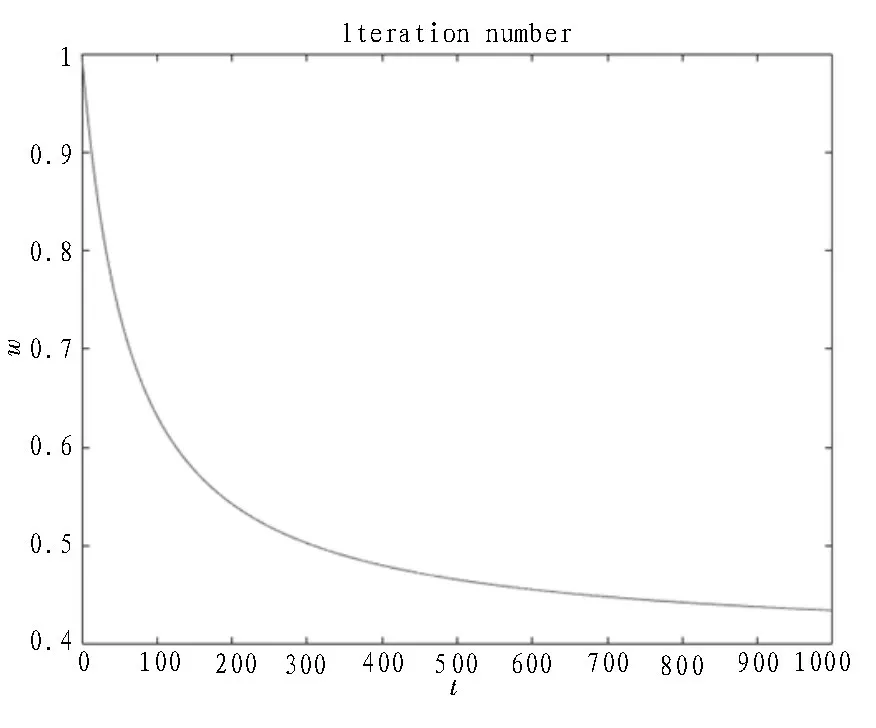
圖2 指數(shù)遞減因子的變化曲線

指數(shù)遞減結(jié)合果蠅算法的具體公式下，其中t(Iteration)為變異策略。

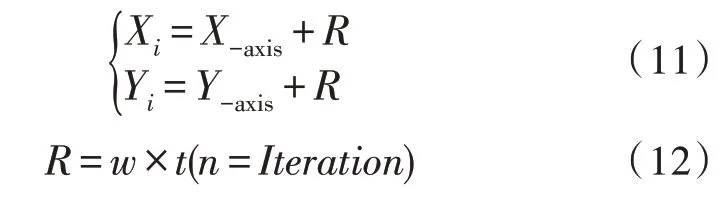
2.2 t變異策略

1908 年，威廉·戈塞[20]首先推導出t分布。t分布圖像形態(tài)與n(自由度)有關(guān)。自由度越小，t分布的曲線愈平坦，曲線中間越低，曲線雙側(cè)尾部越高。自由度n=1 時，t分布的曲線為柯西分布曲線，即t(n=1)=C(0,1)，C(0,1)為柯西分布；自由度越大，t分布的曲線越接近正態(tài)分布曲線[21]；自由度n→∞時，t分布的曲線近似為高斯分布曲線[22]，即t(n→∞)→N(0,1)，其中N(0,1)為高斯分布。即t分布的兩個特殊情況[23]是柯西分布和高斯分布。t分布的自由度分布曲線如圖3所示，在算法優(yōu)化中，t分布自由度的取值為當前迭代次數(shù)。

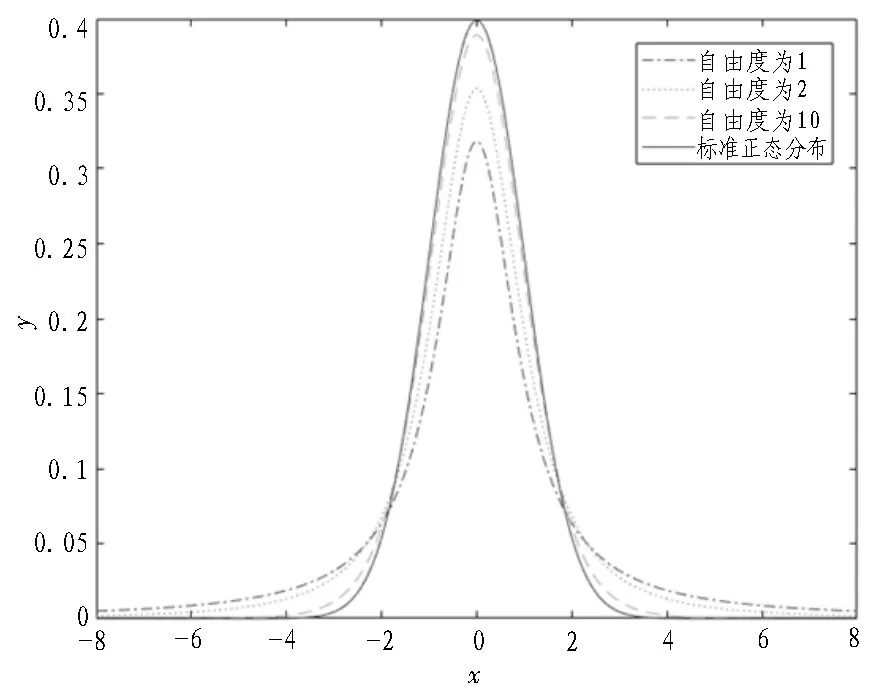
圖3 t分布曲線圖

3 仿真實驗及結(jié)果分析

3.1 測試函數(shù)驗證

為了檢驗算法的有效性，選取了5 個經(jīng)典性能測試函數(shù)對標準果蠅算法和文中優(yōu)化算法在相同環(huán)境下進行Matlab 仿真實驗對比(求最小值)，所選函數(shù)均有不同特性，使用這些函數(shù)進行測試所得的實驗結(jié)果可以全面地反映算法的性能，更具有說服力。

實驗中所采用的經(jīng)典測試函數(shù)如表1 所示。

3.2 固定迭代次數(shù)下實驗仿真分析

在測試函數(shù)過程中，借助Matlab 2016a 平臺，設置迭代次數(shù)為1 500 次，種群規(guī)模為20，算法獨立重復實驗50 次。為了使測試結(jié)果更具有說服力，選取FOA、LGMS-FOA[24]、TEFOA 這3 種算法進行同條件測試，記錄實驗過程中的平均值、標準差和測試函數(shù)最優(yōu)值作為評價標準。實驗中所采用的標準測試函數(shù)如表1 所示，實驗結(jié)果如表2 所示，其中Mean 表示函數(shù)的平均值，Std 表示函數(shù)的標準差，Best 表示函數(shù)可達到的最優(yōu)值，并繪制迭代次數(shù)增加時適應度值的變化曲線。

表1 測試函數(shù)

表2 測試結(jié)果表

測試函數(shù)的變化曲線如圖4～8 所示。

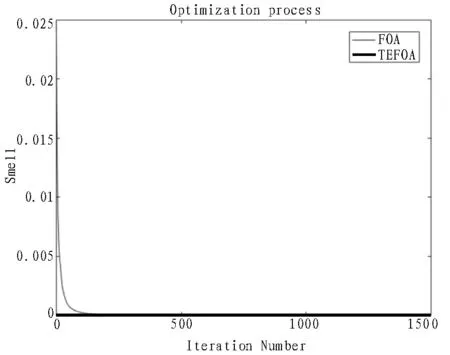
圖4 Sphere函數(shù)變化曲線

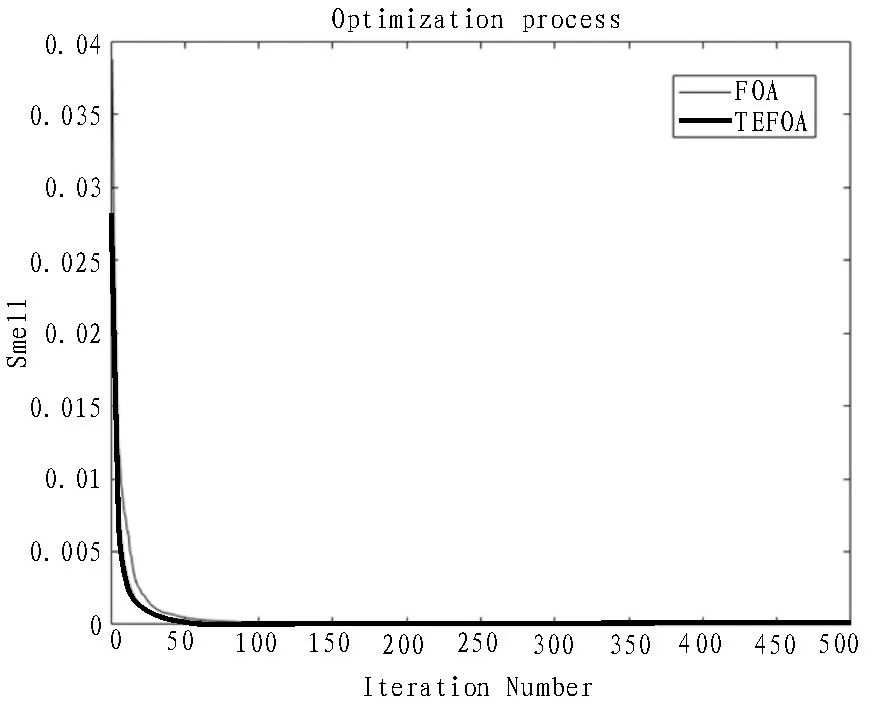
圖5 Griewank函數(shù)變化曲線

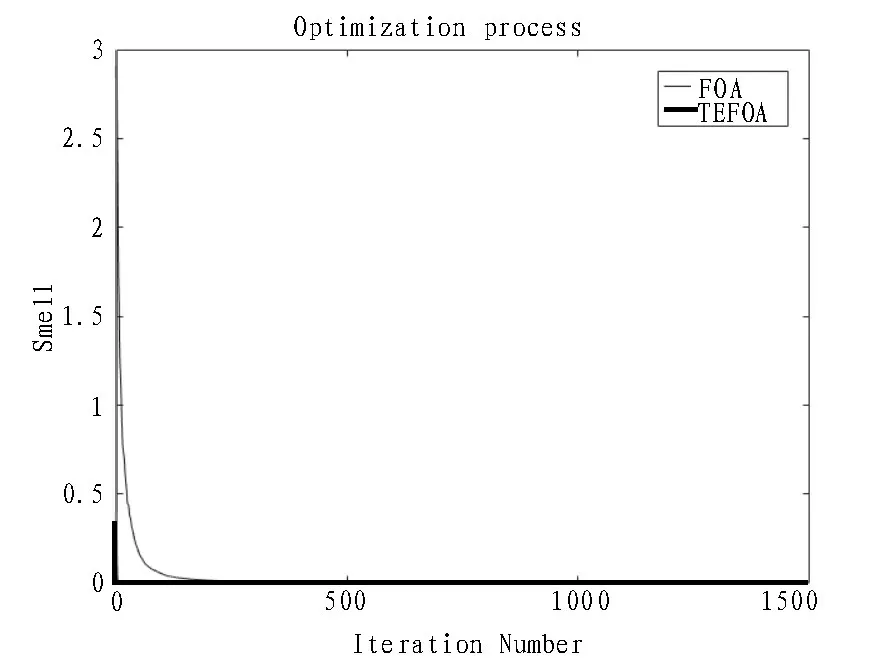
圖6 Rastrigin函數(shù)變化曲線

4 結(jié)束語

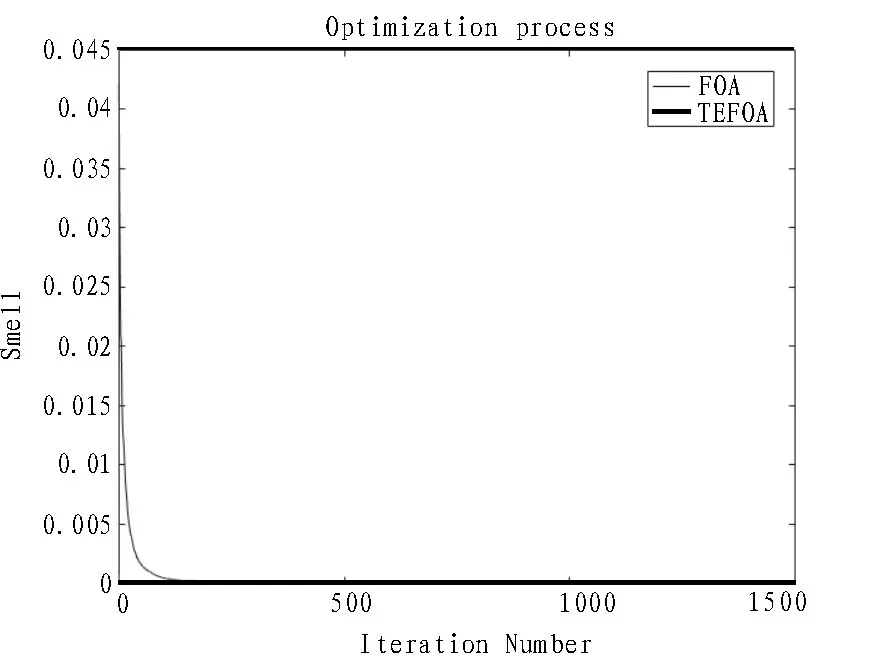
圖7 Schaffer函數(shù)變化曲線

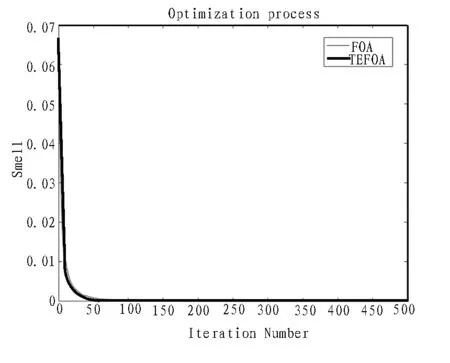
圖8 Sum Squares函數(shù)變化曲線

通過對實驗結(jié)果進行分析可知，盡管函數(shù)對于不同的算法有著不同的尋優(yōu)精度，但在5 種標準函數(shù)的測試中，文中優(yōu)化算法比標準FOA 算法的運算精度均有不同程度的提高。所以，提出的TEFOA 算法優(yōu)于傳統(tǒng)的FOA 算法，尤其是在Rastrigin 和Schaffer 兩個測試函數(shù)上表現(xiàn)優(yōu)異，在迭代過程中訓練得出的最優(yōu)值均可達到函數(shù)本身的最優(yōu)值；另外，從適應度值的變化曲線可以看出，平均迭代不到500次就可獲得最優(yōu)值，TEFOA 算法的收斂速度優(yōu)于傳統(tǒng)的FOA 算法，收斂速度得到了較大的提高。這充分說明了文中的改進算法具有更高的收斂精度、更優(yōu)的搜索能力和更快的收斂速度，在一定程度上也可以避免局部最優(yōu)[25-26]。

FOA 算法是近年來提出的種群智能優(yōu)化算法，但傳統(tǒng)的果蠅算法存在著局限性和不足之處，如難以跳出局部最優(yōu)值、收斂緩慢、精確度不高等。文中考慮到這些方面的問題，在優(yōu)化算法中對果蠅算法的移動步長部分作了指數(shù)調(diào)整策略，即在迭代的初期階段保留了算法較大的搜索步長，也保留了迭代后期算法的精細搜索能力；并在果蠅位置更新時添加擾動策略，避免算法難以跳出局部最優(yōu)解。經(jīng)Matlab 平臺對標準函數(shù)進行測試實驗，結(jié)果表明，文中的算法改進使得算法易陷入局部最優(yōu)和收斂速度慢的不足得到了優(yōu)化，并提高了求解效率。接下來的任務是將改進算法應用于實際問題，驗證解決實際問題的能力。