基于混合插值的機械升降臂控制系統設計
孫曉林,沈宏亮,楊立奎,曹新宇
(1.國網雄安新區供電公司,河北雄安 071600;2.國網河北省電力有限公司,河北石家莊 050000;3.國網河北電科院,河北石家莊 050000)
在機械制造領域中,隨升降臂結構體所承擔執行任務總量的增加,個別處置行為會出現明顯的實用誤差[1-2]。為避免上述情況的發生,傳統輪式控制系統在尋跡閉環的支持下,直接計算與臂體相關的機械性控制指標,再聯合轉向定位算法,確定各項指標的實際作用范圍[3]。但該系統很難完全抑制非合理升降指令的產生,易導致實控誤差結果的不斷增大。
混合差值可用來填充因圖像變換而產生的像素空隙,在離散數據的支持下,該項應用理論可在非關聯信息參量中插入多個連續函數,從而使得既定連續曲線能夠全部通過給定的離散型數據節點。所謂差值是使數值計算結果無限逼近離散函數的處理方法,隨著函數點取值理論的實施,差值計算量可在其他應用位置處對各個節點的近似數值結果進行初步估計,從而使各個像素空隙得到填充與彌補。
因此,為解決傳統控制系統存在的不足,基于混合插值設計了一種新的機械升降臂控制系統,在電動升降器、控制傳感器等多個硬件執行設備的支持下,確定最終的升降臂運動姿態行為。
1 機械升降臂控制系統硬件設計
機械升降臂控制系統硬件執行環境由混合型機械驅動電路、電動升降器、控制傳感器三部分共同組成,具體搭建方法如下。
1.1 混合型機械驅動電路
混合型機械驅動電路如圖1 所示。
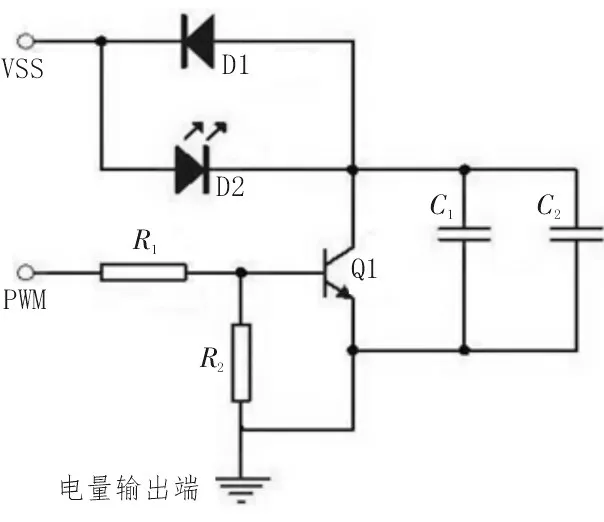
圖1 混合型機械驅動電路
圖1 中,混合型機械驅動電路包含一個VSS 輸入端、一個PWM 輸入端和一個末位電量輸出端,可在R1、R2、C1、C2等多個應用電阻設備的作用下,實現對控制系統內傳輸電子量的定向調度與處理。VSS 輸入端、PWM 輸入端分別與電網高壓與低壓端相連,可在承接交流傳輸電子的同時,建立與下級電阻設備之間的連接[4]。R1、R2是兩個串聯的執行電阻,在變阻器Q1的作用下,這兩個阻值設備可直接感知C1、C2電容內的電子變動行為,并適當控制電路內的電子傳輸流量,從而滿足D1、D2 設備的實際用電需求。
1.2 電動升降器
電動升降器可接收混合型機械驅動電路中的傳輸電子,并將其直接轉化為變頻輸出電流。驅動電機負載機械電路的輸出導線,并在減速器裝置的作用下,實現對主動臂與從動臂元件的定向化調度[5-6]。
電動升降器結構如圖2 所示。圖2 中,托架位于電動升降器模塊頂端,可鞏固驅動電機、減速器等設備結構體之間連接的穩定性,從而使機械升降臂的運動行為逐漸趨于流暢。主動臂、從動臂之間始終保持相對穩定的連接附屬關系,當驅動電機的輸出行為發生改變時,主動臂會出現明顯的運動趨勢,此時從動臂也會隨之產生小幅度的擺動[7-8]。

圖2 電動升降器結構圖
1.3 控制傳感器
控制傳感器結構如圖3 所示。

圖3 控制傳感器結構圖
圖3 中,控制傳感器以濾波放大器作為核心搭建裝置,可在R3、R4、R53 個定值電阻的作用下,調節機械升降臂結構體內的控制電流與控制電壓,從而使系統內部的電量應用需求得到充分滿足。R6變阻器位于控制傳感器上端,可根據R3、R4、R5電阻的實際情況接入阻值,控制元件兩端的電壓負載量,在傳感器元件內傳輸電流保持穩定的情況下,隨變阻器兩端應用電壓負載實值的提升,核心主機對機械臂升降行為的控制精度也開始出現逐漸下降的變化趨勢[9-10]。GND 設備位于R5電阻下端,直接與控制電流輸出端相連,可整合傳感器元件內的所有應用電子量,并將其以交變電流的形式,傳輸至下級系統應用結構體之中。
2 機械升降臂控制系統軟件設計
在各項硬件設備元件的支持下,按照升降臂空間位置表示、控制節點初始化、運動姿態定義的處理流程,搭建系統的軟件執行環境,兩相結合實現基于混合插值機械升降臂控制系統的順利應用。
2.1 升降臂空間位置表示
升降臂空間位置描述了機械控制系統的平均運動范圍,在不考慮其他外界干擾條件的情況下,受到機械臂升降速度、臂擺轉動角度兩項物理量的直接影響[11-12]。機械臂升降速度常表示為,在既定控制時間內,該項物理量的實際值相對穩定,不受除控制周期 |T|外其他物理量的影響。臂擺轉動角度常表示為β,在混合差值原理的作用下,該項物理量的實際值始終小于最大轉動角度βmax。聯立上述物理量,可將升降臂的運動空間位置表示為:
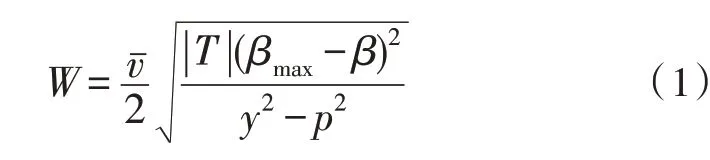
其中,y代表差值應用常量,p代表與機械升降臂相關的混合理論應用系數。
2.2 控制節點初始化
控制節點初始化以控制軟件復位作為起始處理環節,在混合差值原理的支持下,可對機械升降臂體表面的各項應用系數參量進行初步的定義與度量。當CAN 控制總線的波特率數值保持不變時,機械升降臂的運動范圍會始終處于額定范圍區間內;而隨著運動控制時間的延長,CAN 總線的波特率數值會出現明顯提升的變化趨勢,直至將所有混合差值參量完全與待處置節點匹配起來[13-14]。當電動升降器的執行參數恢復至原始狀態后,各項初始參數的指標水平才會逐漸達到理想化的數值標準。
控制節點初始化原理如圖4 所示。
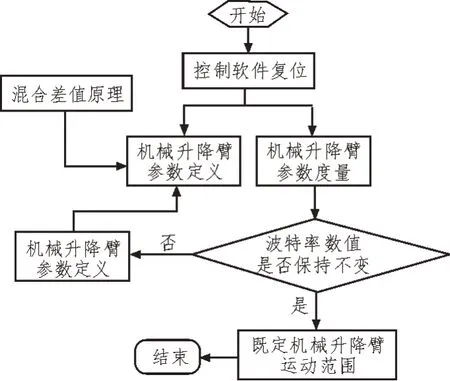
圖4 控制節點初始化原理
2.3 運動姿態定義
運動姿態定義是基于混合插值機械升降臂控制系統設計的末尾處理環節,可聯合多項物理應用系數確定系統的實際控制能力,從而實現對機械臂升降行為偏差的有效避免[15-16]。設λ代表與機械升降臂相關的位姿運動系數,規定在下限運動極值和上限運動極值之間,該項物理量不會出現明顯上升或下降的變化趨勢,而始終與升降臂控制權限均值保持相同的變化狀態。在上述物理量的支持下,聯立式(1),可將基于混合差值原理的機械升降臂運動姿態定義為:
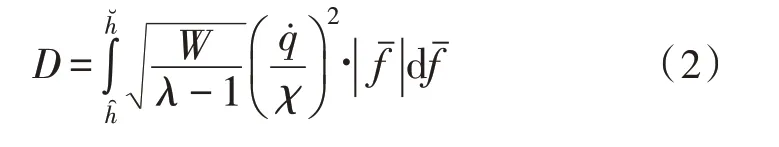
其中,χ代表既定的機械臂升降周期頻度系數,代表與混合差值原理相關的臂體控制參量。至此,實現各項軟、硬件執行環境的搭建,在混合差值原理的支持下,完成新型機械升降臂控制系統設計。
3 系統應用能力檢測
為驗證基于混合插值機械升降臂控制系統的實際應用價值,設計如下對比實驗。選取一個執行能力相對穩定的機械升降臂結構體作為實驗對象,當臂身得到完全伸展時,記錄各項實驗指標的具體數值。實驗組主機搭載基于混合插值的機械升降臂控制系統,對照組主機搭載傳統輪式控制系統。實驗所用機械升降臂結構如圖5 所示。
圖5 機械升降臂結構體
IUD 指標能夠反映系統對機械臂升降行為的實控誤差水平,通常情況下,指標數值越大,實控誤差也就越大,反之則越小。表1 記錄了實驗組、對照組IUD 指標的具體變化情況。
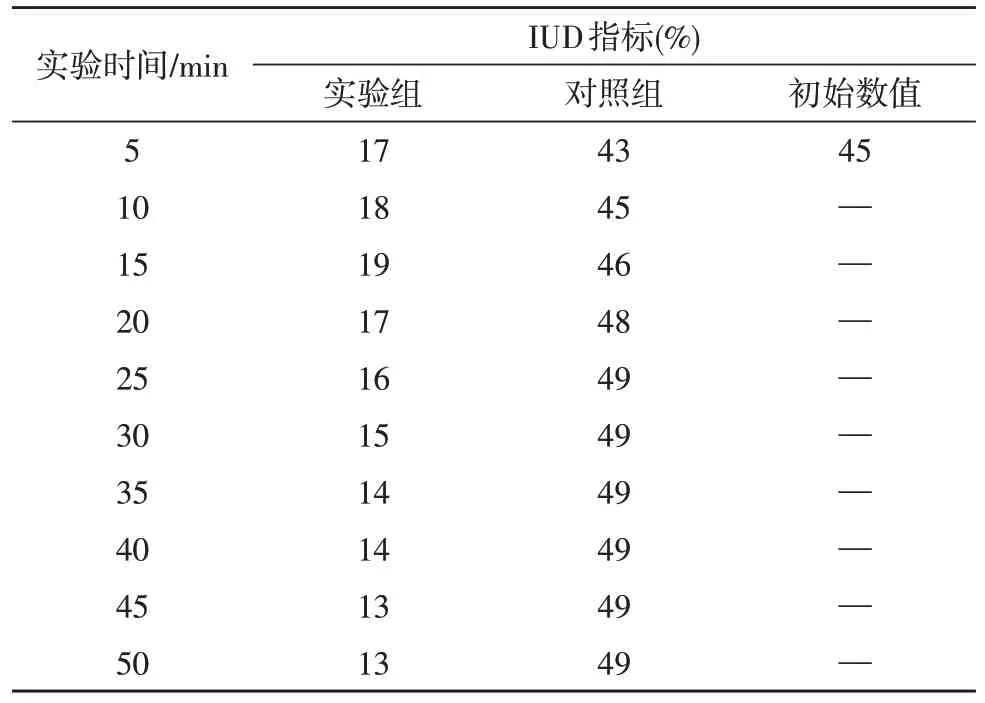
表1 機械臂升降行為的實控誤差對比表
分析表1 可知,理想狀態下與機械臂升降行為相關的IUD 指標數值始終保持不變。實驗組IUD 指標則在小幅上升后,開始持續下降,全局最大值僅達到19%,與初始極值相比,下降了26%。對照組IUD指標在小幅上升后,開始趨于穩定,全局最大值達到49%,與實驗組極值相比,上升了30%。綜上可知,隨著基于混合插值機械升降臂控制系統的應用,IUD指標確實出現了明顯下降的變化趨勢,可從根本上解決核心主機對機械臂升降行為的實控誤差水平過高的問題。
LEA 指標能夠描述系統非合理升降指令的產生數量,一般情況下,LEA 指標數值越大,系統產生的非合理升降指令數量也就越多,反之則越少。表2記錄了實驗組、對照組LEA 指標的實際變化情況。

表2 非合理升降指令的數量對比表
分析表2 可知,理想狀態下與非合理升降指令生產數量相關的LEA 指標數值始終保持不變。實驗組LEA 指標在一段時間的穩定狀態后,開始出現持續性下降的變化趨勢,從第40 min 開始,又開始逐漸趨于穩定,全局最大值僅達到33%,與初始數值相比,下降了21%。對照組LEA 指標則保持先上升、再穩定、最后不斷下降的變化趨勢,全局最大值達到56%,與實驗組極值相比,上升了23%。綜上可知,隨著基于混合插值機械升降臂控制系統的應用,LEA 指標也出現了明顯下降的變化趨勢,滿足系統主機有效控制非合理升降指令產生數量的實際應用需求。
4 結束語
與傳統輪式控制系統相比,基于混合插值機械升降臂控制系統可在混合型機械驅動電路、電動升降器等多個硬件設備結構體的作用下,實現對升降臂臂身運動姿態的精準定義,且可在完成控制節點初始化的同時,得到明確的升降臂空間位置表示結果。從實用性角度來看,IUD 指標、LEA 指標的快速下降,可解決核心主機對機械臂升降行為實控誤差水平過高的問題,在精準化控制方面,可使臂體結構的基本應用需求得到有效滿足。

