基于Stackelberg博弈法的光伏消納模型設計與仿真計算

劉安諾，井天軍，何 欣，王維洲

（1.中國農業大學，北京 100083；2.國網甘肅省電力公司 電力科學研究院，甘肅蘭州 730000；3.國網甘肅省電力公司，甘肅蘭州 730030）

隨著新能源產業的不斷發展，光伏發電在電力系統中所占比例不斷提高[1]。然而，由于光伏發電存在隨機性、波動性等問題，高比例光伏電源的接入，引起了電網的電能質量變差等問題[2]，同時，還導致電網下網的潮流變輕，出現倒送的可能，甚至在嚴重情況下使部分區域的網供負荷特性發生一定的改變，導致電網供需平衡的難度進一步加大[3]。因此，合理消納光伏電量成為目前新能源電力發展中亟待解決的問題。文獻[4]根據非合作博弈理論，構建了多個微電網調度優化模型，各微網間通過電能交換的方式進行電力轉移，在電力不足或富余時可通過從外電網采購或銷售電力的方式匹配負荷需求。文獻[5]從電力供需側間互動博弈的角度出發，研究智能用電策略，供電側可通過調整電價的方式緩解用電高峰時段的供電壓力，需求側可通過對電價的響應，調整自身用電習慣，降低用電成本。文獻[6]研究了包含能源運營商、分布式光伏用戶、EV 充電代理商等多參與主體的綜合能源園區市場交易框架，各方以自身利益最大化為目標進行購售電價的非合作博弈，在平衡各方收益、降低系統用電成本的前提下，達到促進光伏消納的效果。

光伏消納模型涉及多方參與，需要建立多目標優化模型，并進行優化計算，現有方法未充分考慮需求響應下的多方博弈均衡狀態。該文基于需求響應驅動的彈性矩陣，提出了一種基于Stackelberg 博弈法的光伏消納模型，建立了多方博弈均衡狀態下的優化目標函數，并通過改進粒子群算法進行求解，對模型的有效性進行了驗證。

1 光伏消納模型設計

1.1 電力需求響應彈性矩陣

在實際應用中，需求側的電力用量具有隨電價變化的屬性。因此，在基于博弈法的光伏消納分析中，首先需要建立基于價格驅動的用電負荷轉移模型，對這一變化進行定量分析。在該模型中，實際的用電負荷受電價波動的影響。為計算其影響程度，引入了需求響應價格驅動模型。在該模型中，構建了需求側的電量電價彈性矩陣，衡量需求側受電價驅動的程度，并作為計算基礎，對博弈模型中雙方達成的一種電量和電價均衡狀態進行定量計算。

需求側用戶對電價的反映情況可以用電量電價彈性矩陣來描述，該矩陣的理論基礎為電量電價彈性，即電量變化率與電價變化率的比值[7]，如式（1）和（2）所示。式（1）表示電量電價的自彈性系數，式（2）表示電量電價的交叉彈性系數。

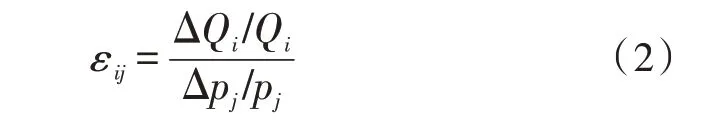
其中，i和j表示不同的時點，Qi表示i時點測得的對應時段的用電量，ΔQi表示由于價格變動而引起的用電量的變化量，pi和pj分別代表i和j時點的電價，Δpi表示i時點的電價變化。

電力電價彈性矩陣如式（3）所示，由此可得實施峰平谷分時電價后需求側各時段的用電需求量變化情況，如式（4）所示：

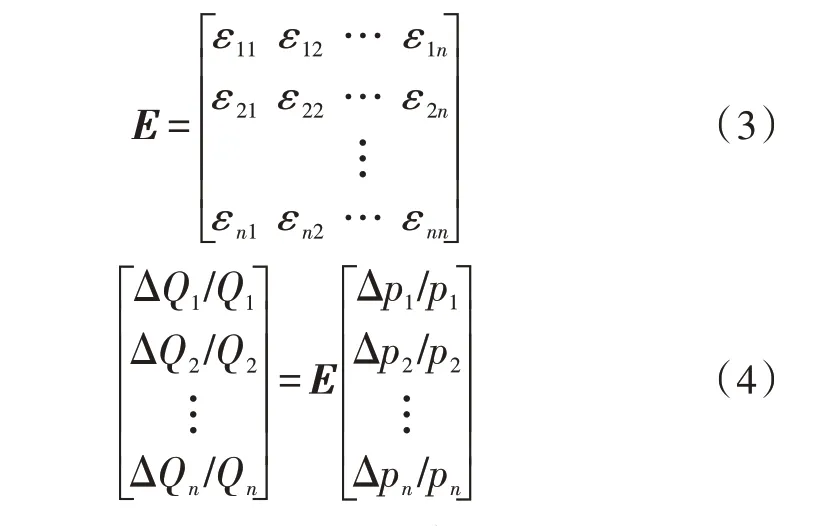
其中，E為電力電價彈性矩陣，n為電價劃分時段數。

綜上，實行分時電價后各時段的實際用電量可用式（5）求得：

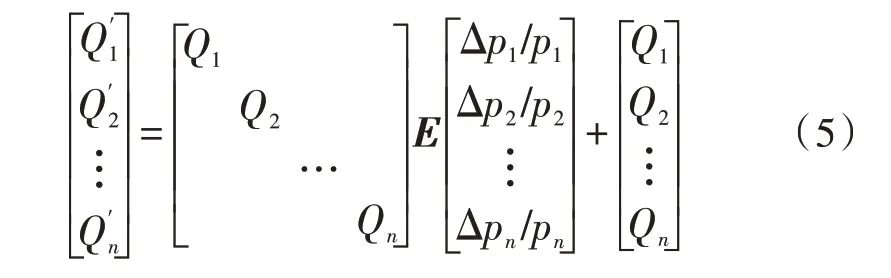
1.2 基于Stackelberg博弈法的光伏消納模型

為對光伏消納背景下用能側各方參與的影響進行分析，基于式（1）～（5）的分析結果，首先對供給側和需求側分別建立目標函數。

對于供給方，其目標收益為售電收益減去購電成本。其目標函數計算公式為：

其中，pf、pp、pg分別為峰平谷時段的售電電價，P0為供給側的光伏發電量收入，c為供給側的單位購電成本。實際的qi、qj、qk受光伏出力情況的約束。

在電量消納過程中，需求側的收益函數即為購電成本的負值，該值的升高即表示購電的成本較少。其目標函數計算公式為：

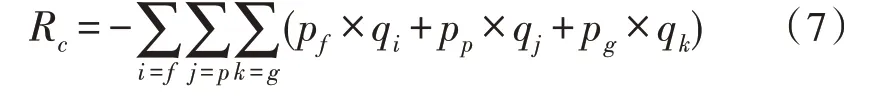
由式（6）與式（7）的目標函數計算公式可得，供給側與需求側的目標函數并不一致，因此該優化過程為多目標函數的優化過程。為對該光伏電量消納過程中的多目標函數進行優化，引入Stackelberg 雙寡頭博弈模型，對該多目標函數進行轉換。

根據納什均衡的定義可得，市場主體交易決策的出發點均為自身收益最大化[8]。通過反復的博弈達到納什均衡點時，任何一方市場參與者單方面改變策略均無法使其他參與者改變交易策略以獲得更多的收益。在Stackelberg 雙寡頭模型中，要求參與方充分了解彼此的成本和市場需求情況[9-12]，在該模型中主要涉及兩方參與者：領導者與追隨者。Stackelberg 博弈法可用來分析存在不同行動次序對象的動態博弈，符合電力產業鏈中的行為情況。供給側視需求側在不同電價下的用電量為已知情況，進而調整其定價策略；需求側視供給側各時段的電量供應及電價水平已定，以調整自身生產情況中各用電時段的分配。該電力交易中的博弈主要來自雙方均出于使自身利益最大化的目的進行購售電策略的選擇。通過雙方的博弈，達到各時段電量與電價的均衡狀態，實現需求側的用電優化[13]。

根據供給側與需求側的收益函數，考慮供給側作為博弈中的追隨者，需求側作為博弈中的領導者的情況，即供給側已知需求側的歷史負荷需求情況并能以此測算出其電量電價彈性的情形下，以供給側利益最大化為目標，需求側購電成本降低為約束條件的交易策略，利用Stackelberg 博弈法求取該模式下市場電力交易的最優解。由此，原多目標優化函數轉換為單目標優化函數，其目標函數計算公式為：

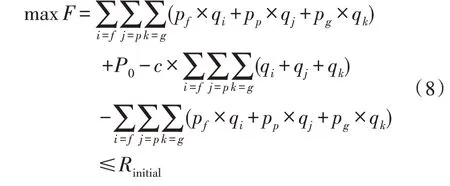
其中，Rinitial為優化前的原始值。

2 改進粒子群求解算法

式（8）的優化模型為非線性函數。為對該目標函數進行求解，應用了改進的粒子群算法[14]，求取Stackelberg 非合作博弈模型的納什均衡解。

粒子群算法模型包括D維空間，N個粒子，其中，每個粒子主要由3 個變量定義，第i個粒子由3 個D維空間向量表征，分別為：

當前粒子位置：

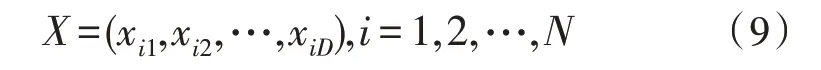
第i個粒子的飛行速度：

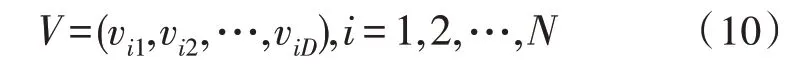
記錄第i個粒子的歷史最優位置：

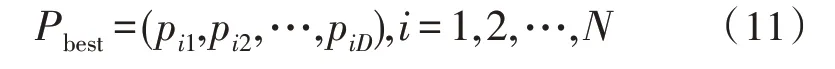
記錄搜索到的全局歷史最優粒子位置：

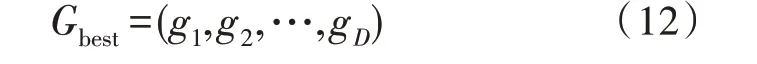
對于每一個粒子，其D維速度及位置根據下式更新：

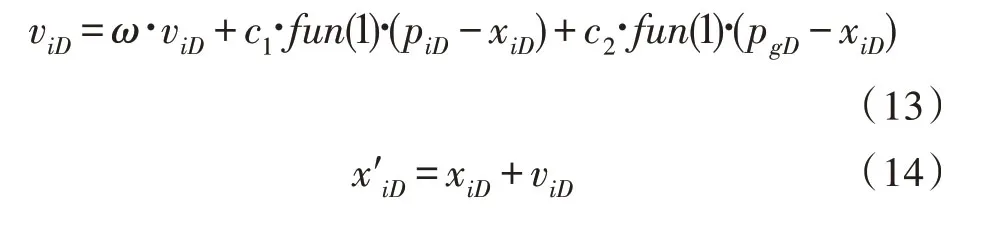
其中，ω為慣性權重，其決定了粒子先前的飛行速度對當前更新速度值的影響程度；c1和c2為粒子學習因子，通常取值為2；fun(1)為可以生成[0,1]范圍內數值的隨機函數。

此外，粒子的速度因求解問題的特殊性可以設定不同的范圍[Vmin,Vmax]，即在執行速度按式（12）更新后，需對當前生成的下一時點的速度值進行取值的判斷。

該文對目前已有的粒子群算法進行了部分改進，使得算法運行效率得以提高，且對最優解的求取有了更好的表現效果。主要改進處如下：

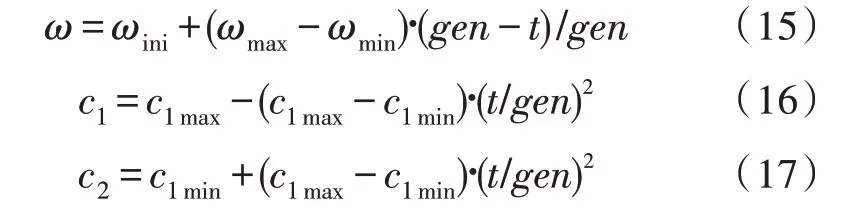
其中，gen為迭代次數，t為當前迭代代數。

此外，該文考慮到每個粒子產生變異的可能性，引入隨機變異的部分粒子，以進一步優化算法，避免過早收斂的可能性[15]。

通過對粒子群算法中部分公式的改進，使得在算法搜索初期全局搜索權重較高，后期局部搜索權重較高，在一定程度上避免粒子群算法陷入局部最優的情況[16]。

利用改進的粒子群算法模擬供給側與需求側的博弈過程，通過迭代尋優，利用式（13）和（14）不斷更新博弈過程中雙方的最優選擇，最終在解空間內求得當前約束條件下雙方交易的最優策略。

綜上，粒子群迭代求解算法的基本流程如圖1所示。

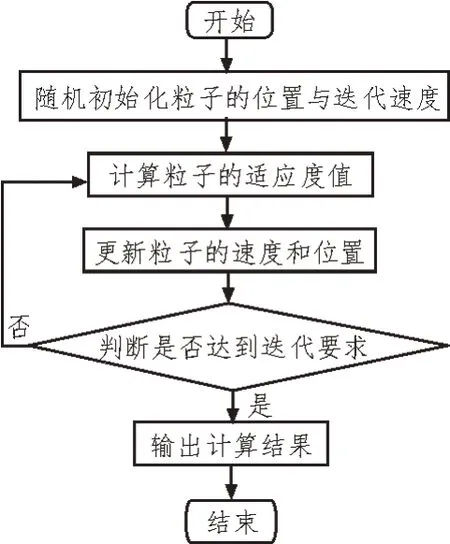
圖1 粒子群迭代求解算法流程

3 算例分析

為驗證模型的有效性，采用甘肅省某產業園的數據作為算例進行分析。在原運行條件下，產業園的峰平谷時段電價分別為0.656 4 元/kW·h、0.438 9 元/kW·h和0.221 5 元/kW·h。峰時段日均負荷為881.525 kW，平時段日均負荷為477.375 kW，谷時段日均負荷為1 073.3 kW。

利用前述優化的粒子群算法，求解供給側和需求側的電力交易模型，結果如圖2 所示。最終求得最佳情況下供給側的日收益為108.60 元，此時對應的峰平谷時段電價分別為0.787 7 元/kW·h、0.417 0 元/kW·h 和0.221 5 元/kW·h。

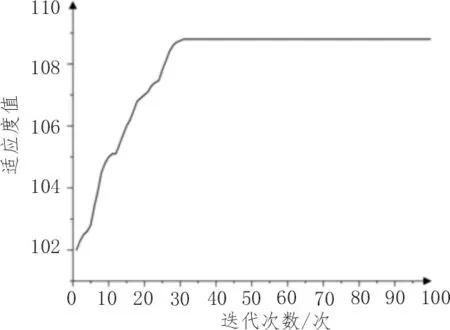
圖2 粒子群優化算法結果

博弈前后的峰平谷電價情況，如表1 所示。

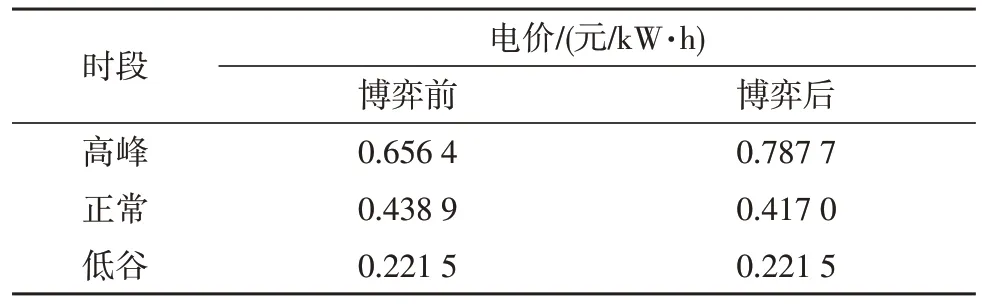
表1 博弈前后峰平谷時段電價對比

該模式下求得供給側的收益為R=108.60 元/天；需求側購電的平均電價為C=0.313 3 元/kW·h（原平均單位購電價為0.407 1 元/kW·h）

博弈前后的產業園峰平谷負荷分配情況，如表2所示。

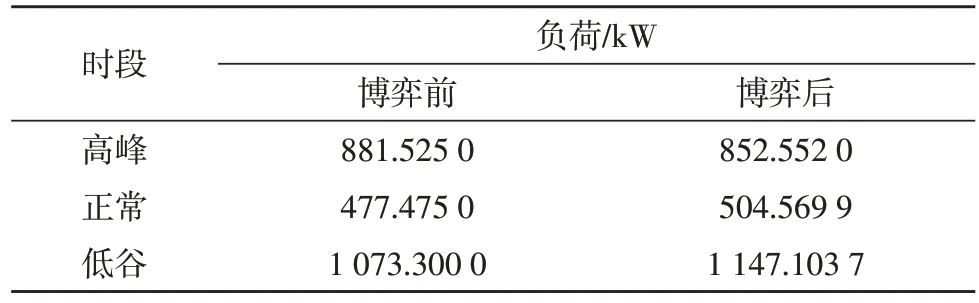
表2 博弈前后峰平谷時段日均負荷對比

由結果可知，峰谷拉開比由原來的0.821 3 變為0.743 2，降低了9.51%。峰時段日負荷也由原來的881.525 0 kW 變為852.552 0 kW，在一定程度上起到了削峰填谷的效果。

算例仿真結果表明，通過該模式可以優化需求側的用電結構，在保證需求側購電成本降低的前提下，實現供給側效益最大化的效果。通過Stackelberg非合作博弈的模式，實現了需求側和供給側收益的共同提高，從而顯著促進了光伏電量的消納[17-18]。

4 結束語

該文針對目前存在的光伏就地消納的問題，建立了光伏消納背景下用能側各參與方的優化模型。為分析實際光伏消納過程中存在的多方收益均衡問題，模型中考慮了供給側、需求側的收益函數，解決了目前購售電端存在的信息不對稱情況，并利用基于Stackelberg 博弈法的模型構建多方共贏的交易策略，以供給側利益最大化，需求側購電成本降低為模型約束條件，求解了雙方最優交易策略。通過算例仿真分析，得出結論如下：

1）供給側通過制定合適的電價策略，可以驅動需求側改變用電習慣，從而一方面可以更好地匹配光伏出力情況；另一方面使得需求側用電成本降低，通過這種模式實現供給側收益最大化的效果。

2）通過供給側與需求側的博弈，不僅可以提高雙方的目標收益，同時可以起到促進光伏消納、削峰填谷的作用，顯著提高了光伏消納能力。

3）基于文中提出的采用Stackelberg 博弈法建立服務商與產業園間電力交易的博弈模型，后期可考慮引入區塊鏈技術進行自動化、智能化的電力交易，使得各時點的電力交易更具針對性、高效性。