基于EMD與IMF分量統計特性的ECG去噪

盧莉蓉，牛曉東，王鑒，李春燕

1.長治醫學院生物醫學工程系，山西長治046000；2.長治醫學院基礎醫學部，山西長治046000；3.中北大學信息探測與處理山西省重點實驗室，山西太原030051；4.山西北方機械制造有限責任公司工藝技術研究所，山西太原030051

前言

心電圖（Electrocardiogram, ECG）是記錄心臟的生物電活動，在臨床上廣泛用于心血管疾病的診斷。然而，ECG 信號屬于非線性、非平穩弱電信號，容易被各種噪聲污染，嚴重影響P、QRS、T 特征波檢測和RR 間期識別的正確性，并最終導致心臟疾病的誤診［1］。因此，ECG信號去噪對臨床診斷的正確性具有重要的意義。ECG 信號中的噪聲主要包括工頻干擾、基線漂移噪聲和肌電干擾噪聲等［2-3］。其中，50 Hz工頻干擾可利用陷波器有效地去除；基線漂移噪聲的頻率一般低于1 Hz，表現為ECG 信號偏離正常基線，并呈現緩慢波動的特點；肌電干擾噪聲的頻譜較寬，頻率一般為5 Hz～2 kHz，與ECG 信號頻譜重疊。一般表現為ECG 信號上的高頻噪聲，使得P、QRS、T特征波局部失真，難以識別［4-6］。

針對ECG 信號噪聲特點，相關文獻提出了許多線性和非線性信號處理方法去除ECG 信號噪聲。這些方法主要包括：數字濾波法、自適應濾波法、小波變換法、經驗模式分解（Empirical Mode Decomposition,EMD）法等。數字濾波和自適應濾波具有較強的降噪性能，但由于肌電干擾噪聲與ECG信號頻譜重疊，在濾除肌電干擾噪聲的同時，也會濾除部分ECG 信號［7-9］。小波變換法是常用的ECG 信號去噪方法，但小波變換法是非自適應的，小波函數和閾值的選取對去噪效果有很大的影響［10-13］。EMD法是一種新的自適應信號處理方法，克服了小波的缺點，已廣泛應用于非線性、非平穩信號的分析［3,14-15］。EMD 法首先將ECG 信號自適應分解為一系列的固有模態函數（Intrinsic Mode Function, IMF）分量，其次識別每一個IMF 分量屬于信號分量或噪聲分量，最后通過采用ECG 信號的IMF 分量重構ECG信號實現去噪［14-15］。然而，現有絕大部分文獻采用視覺觀察IMF 分量是否含有明顯QRS 特征波，經驗性判斷IMF 分量屬于ECG 信號分量還是噪聲分量，不具有通用性，有很大的主觀性，使得ECG 信號的去噪結果存在偏差［16-18］。

針對EMD 方法去除ECG 噪聲的缺點，本文將利用EMD 與IMF 分量的統計特性對含有基線漂移噪聲與肌電干擾噪聲的ECG 信號進行去噪處理。本方法首先對含噪ECG 信號進行EMD 分解得到一系列IMF分量，然后利用噪聲IMF分量的統計特性識別出所有噪聲IMF 分量，則剩余IMF 分量即為ECG 信號分量，最后采用信號屬性IMF分量重構ECG信號。

1 方法理論原理

含有基線漂移噪聲與肌電干擾噪聲的ECG 信號經EMD 分解，自適應得到頻率由高至低一系列IMF分量。IMF 分量可分為3 種具有不同物理意義的類型：（1）高頻噪聲IMF 分量，一般屬于肌電干擾的高頻分量；（2）ECG 信號IMF 分量；（3）低頻噪聲IMF 分量，一般屬于基線漂移分量或數據有限長引起的偽IMF分量。

1.1 高頻噪聲IMF分量統計學識別原理方法

對于高頻噪聲IMF 分量，采用文獻［19-20］給出的統計去噪方法進行去除。其原理簡述如下：

首先，EMD 分解高斯白噪聲等效于一個恒定品質因素的二進濾波器組，分解得到的IMF 分量滿足：（1）分解得到的第i個分量IMFi的平均周期正好是前一分量IMF（i-1）平均周期的兩倍；（2）IMF 分量的功率譜正態分布，且在功率譜-平均周期（取對數）圖上，IMF的功率譜面積相同。基于（1）和（2），得到IMF能量密度與其相應平均周期的對數之和為常數［19-20］，即：

其中，Ei為第i個IMF 分量的能量密度，常 為第i個IMF 分量的平均周期。對于歸一化的高斯白噪聲序列，式（1）中常數為零，即：

式（2）表示高斯白噪聲lg常與lgE的期望直線。能量密度的擴展函數為［19-20］：

其中，x= lg，k 是由標準正態分布的百分位數確定的常數，對于95%的置信區間，k=1.645。

對于采集良好的數據，包括ECG 信號數據，其IMF1 總是噪聲，且一般可等效為高斯白噪聲分量。因此，可以基于IMF1 并采用上述白噪聲統計特性估計數據的噪聲IMF 分量。如果IMF 落在以IMF1 為基礎構造的噪聲期望直線的置信區間內，即可判斷識別為噪聲IMF分量。

1.2 低頻噪聲IMF分量統計學識別原理方法

寬頻譜肌電干擾噪聲常等效于白噪聲，因此，含噪ECG 信號的IMF1 是肌電干擾高頻分量且具有白噪聲特點，基于IMF1 并利用第1.1 節統計方法可以有效地識別肌電干擾的IMF 分量。然而，該方法僅對肌電干擾的高頻IMF 分量，即含噪ECG 信號的高頻噪聲IMF 分量有效。低頻噪聲IMF 分量一般由基線漂移、數據有限長引起偽分量等疊加融合構成，其物理屬性一般不屬于單獨的肌電干擾低頻分量，因此，第1.1節方法一般不能識別含噪ECG 信號的低頻噪聲IMF分量。

對于低頻噪聲IMF 分量，本文采用IMF 統計均值特性進行識別。識別原理如下：EMD 分解過程實際為一均值篩選過程。均值篩選過程使得IMF 極值定義的上下包絡對稱，因此，篩選結束后，IMF的均值應為0。然而，由于數據有限長，IMF 端點的上下包絡只能通過方法近似估計。包絡的估計引起端點均值誤差，將隨篩選次數的增加逐漸傳染至IMF 內部，最終，導致IMF 均值偏離理想0 均值。IMF 階數增加，頻率減小，局部尺度，特別是端部局部尺度增大導致端部誤差增大，因此，IMF 均值偏離0 均值程度將隨IMF 階數增大而增大。低頻噪聲的IMF 分量頻率相比ECG 信號的IMF 頻率一般要小的多（基線漂移噪聲的典型頻率為0.15～0.30 Hz［2-3］，ECG信號頻率一般大于1 Hz（60 bpm），其極值定義的局部時間尺度，特別是端部局部時間尺度要遠大于ECG 信號IMF 分量的局部時間尺度，因此，端部估計誤差導致的均值誤差更大，常表現為IMF 分量均值曲線非線性的突變，可以對低頻噪聲IMF分量進行識別。

1.3 基于IMF分量統計特性的ECG去噪方法

基于第1.1 節和第1.2 節的噪聲IMF 統計學特性，本文提出基于EMD 與IMF 分量統計方法的ECG去噪方法，方法步驟如下：（1）含噪ECG 經EMD 分解為一系列IMF 分量；（2）求每一個IMF 分量的lgTˉ與lgE，并基于IMF1為高頻噪聲對所有IMF分量進行顯著性檢驗，識別高頻噪聲IMF分量；（3）對每一個IMF分量進行0 均值檢驗，如果相對低階IMF 分量，存在一個IMF分量明顯偏離0均值，則此IMF分量被識別為低頻噪聲，之后所有IMF 分量也被識別為低頻噪聲；（4）未被步驟（2）、（3）識別的剩余IMF 分量即為ECG 信號分量，將ECG 信號的IMF 分量重建即可得到去噪后ECG信號。

1.4 評價指標

本文選取信噪比（Signal to Noise,SNR）、均方誤差（Mean Square Error, MSE）、自相關系數（Autocorrelation Coefficient, AC）3 個評價指標來對本文方法的去噪效果進行評估，如下所示：

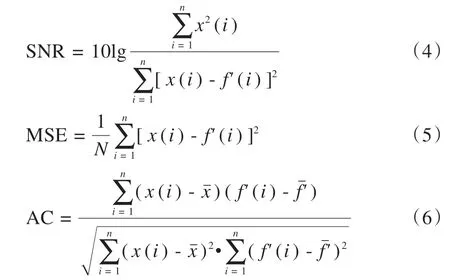
其中，x(n)為原ECG 信號，f'(n)為重建ECG 信號。SNR 越大，MSE 越小，代表該去噪方法的去噪效果越好。AC越大，代表重建ECG信號與“干凈”ECG信號的偏差越小，去噪方法的去噪效果越好。

2 實驗及分析

為了驗證本方法的有效性，本文選取“MIT-BIH Arrhythmia Database”中104、107、200 號ECG 信號，分別疊加“MIT-BIH Noise Stress Test Database”中基線漂移噪聲信號bw 與肌電干擾噪聲信號ma 形成含噪ECG 信 號（“MIT-BIH Arrhythmia Database”與“MIT-BIH Noise Stress Test Database”所提供的信號均為實際采集信號）。分別采用本文方法與經驗法對含噪ECG 信號進行去噪處理，并對其去噪結果進行比較。本文首先通過對含噪107 號ECG 信號進行去噪處理來詳細說明本方法的去噪過程。

2.1 含噪107號ECG信號的去噪實驗

107號ECG信號、肌電干擾噪聲ma、基線漂移噪聲bw與三者疊加形成的含噪107號ECG信號如圖1所示。

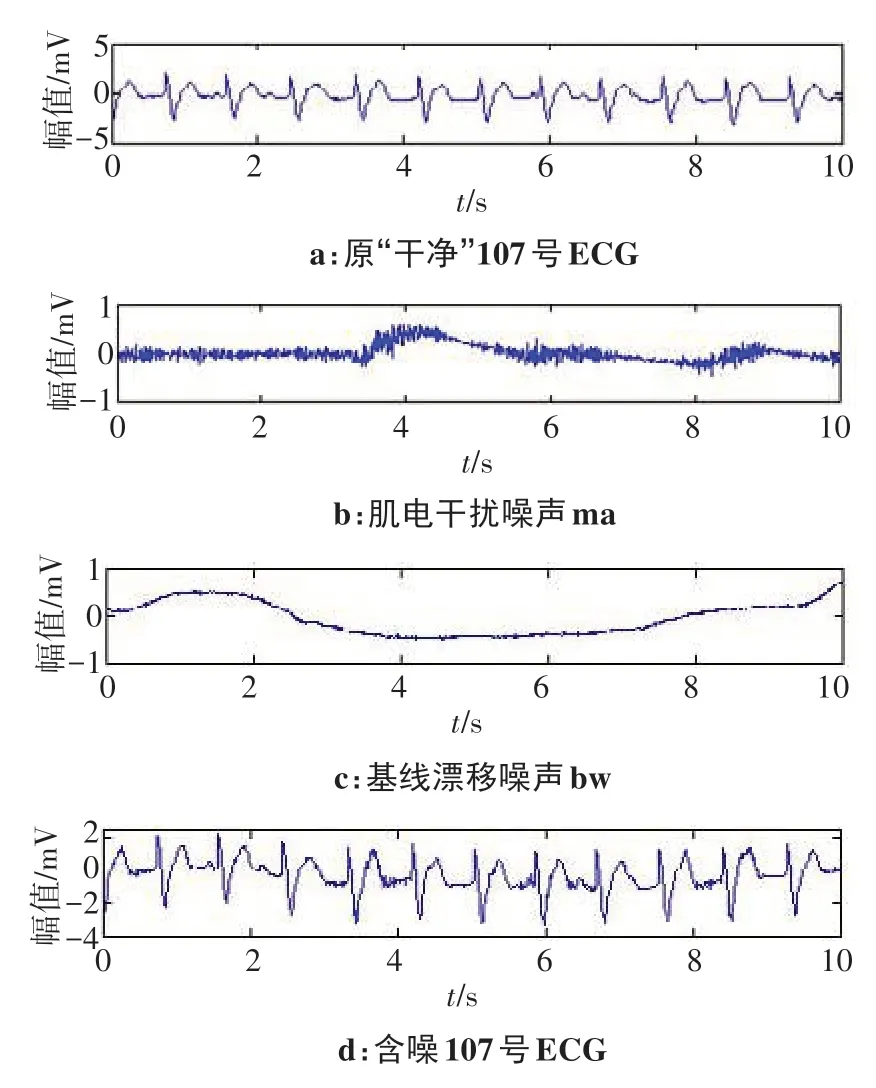
圖1 107號ECG、肌電干擾噪聲ma、基線漂移噪聲bw與含噪107號ECGFig.1 No.107 ECG,electromyography interference noise ma,baseline drift noise bw and No.107 ECG with noise

（1）對含噪107號ECG信號進行EMD分解，可得一系列IMF分量，如圖2所示。

圖2 含噪107號ECG信號經過EMD得到的IMF分量Fig.2 IMF components generated by No.107 ECG with noise after EMD

（2）利用高斯白噪聲IMF 分量的統計學特性對IMF分量進行顯著性檢驗，識別高頻噪聲IMF分量。

以IMF1 為噪聲，并基于式（3）作出IMF 分量lgTˉ與lgE關系的期望直線，選擇95%置信區間［為了便于顯示結果，基于大量的數據實驗，文獻［19］對準則作了適當修改：使用高斯白噪聲方差的3 倍作為上（下）界，代替式（4）決定的95%置信區間邊界］，確定上下邊界，結果如圖3所示。

圖3 中，紅色實線為IMF 分量lgTˉ與lgE關系的期望直線，藍色虛線為95%置信區間的上、下邊界，黑色星點代表每一個IMF 分量的平均周期和相應的能量密度。從圖中可以看出IMF1 的能量密度位于95%置信區間上下界之間，因此判定IMF1 為肌電干擾噪聲IMF分量，舍棄。

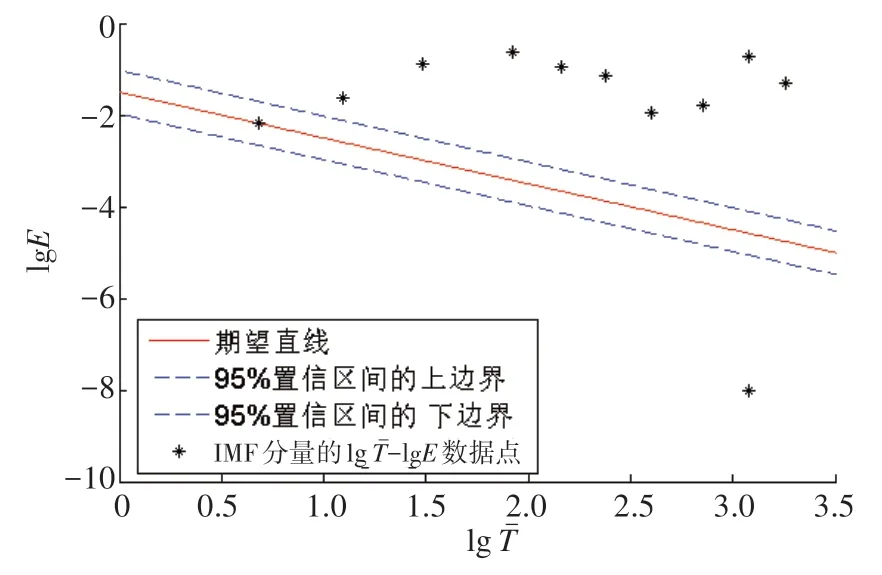
圖3 IMF分量的顯著性檢驗Fig.3 Significance test of IMF components

（3）利用均值檢驗識別低頻噪聲IMF 分量。所有IMF分量的均值—方差的誤差棒圖如圖4所示。

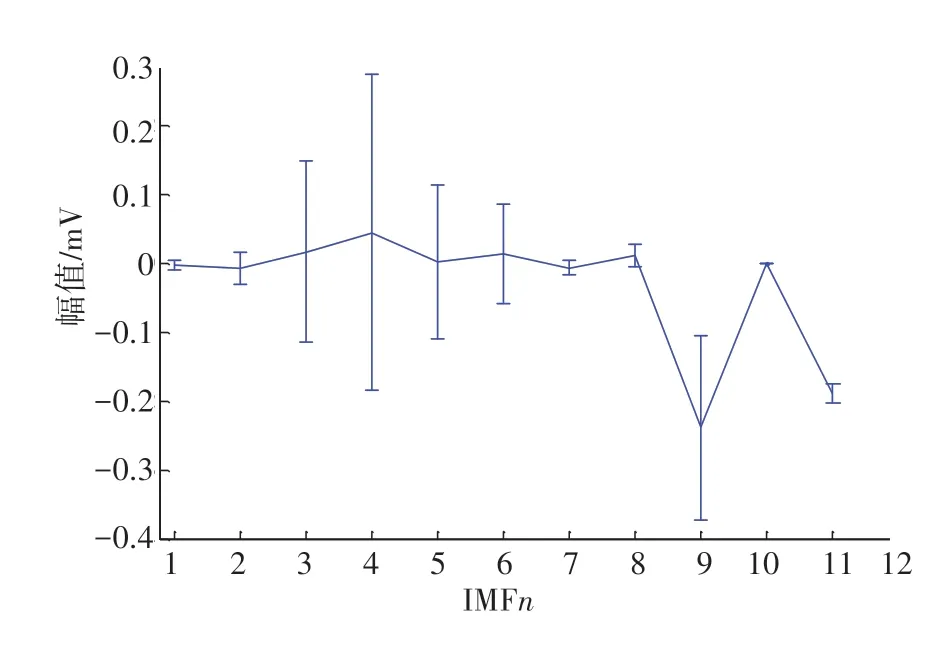
圖4 IMF2-IMF11的誤差棒圖Fig.4 Error bar chart of IMF2-IMF11

從圖4 可以看出，數據端點均值誤差導致IMF2-IMF8 分量的均值在0 均值周圍微小波動，IMF9 分量均值作為一個奇異點使得IMF 均值曲線出現突變，根據第1.2 節判定IMF9 為低頻噪聲IMF 分量與ECG信號IMF 分量的分界。即IMF2-IMF8 分量為信號IMF分量，IMF9-IMF11為低頻噪聲IMF分量。

（4）剩余IMF分量重構得到107號ECG信號。第（2）步識別IMF1 為高頻噪聲IMF 分量，第（3）步識別IMF9～IMF11為低頻噪聲IMF分量，則剩余IMF2～IMF8分量為ECG信號IMF分量。IMF2～IMF8分量重構107號ECG信號結果如圖5所示。

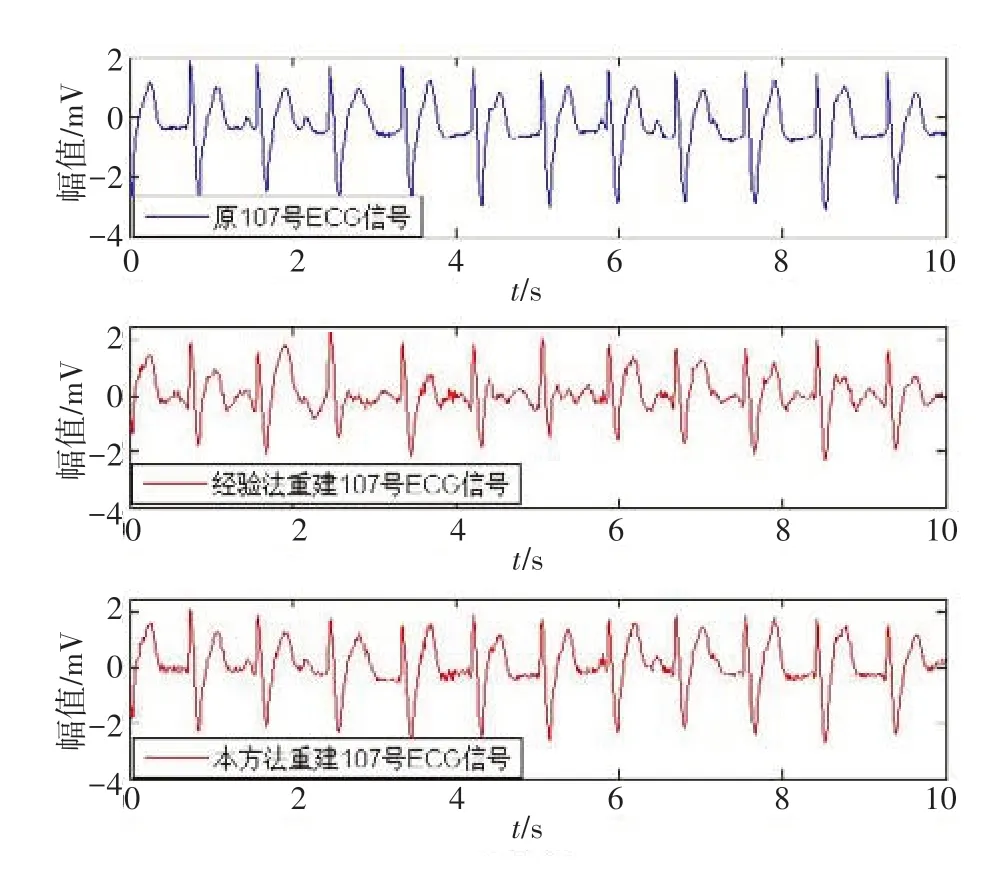
圖5 兩種方法重構107號ECG與原107號ECG對比圖Fig.5 Comparison of No.107 ECG reconstructed by two methods and original No.107 ECG

2.2 實驗結果分析

為了驗證本方法的有效性，采用基于QRS 特征波通過視覺觀察經驗性對107 號ECG 信號去噪，“經驗法”識別為：IMF1-IMF4 包含明顯QRS 特征波，為信號IMF分量，因此采用IMF1-IMF4分量重構107號ECG 信號。兩種方法重構107 號ECG 信號與原107號ECG信號對比圖如圖5所示。

從圖5 可以看出，利用經驗法重構的107 號ECG有效去除基線漂移噪聲與肌電干擾噪聲，但導致明顯畸變，特別是特征波幅值的嚴重畸變。本方法有效去除了基線漂移噪聲與肌電干擾噪聲，同時重構107號ECG很好保留了原ECG信號的特征波。

除107 號ECG 信號，實驗又選取104 與200 號ECG 信號，分別疊加基線漂移噪聲信號bw 與肌電干擾噪聲信號ma 形成含噪ECG 信號，并采用本方法與經驗法對含噪ECG 信號去噪處理，去噪結果如表1所示。

表1 列出了含噪104 號、107 號、200 號ECG 信號分別采取經驗法與本方法去噪所得ECG 信號的SNR、MSE、AC。從表1 可以看出，相比較經驗法，采取本方法去噪后的SNR 增大，MSE 減小，AC 增大。可知本文提出的基于EMD 與IMF 分量統計特性的ECG去噪方法的去噪效果要優于經驗法去噪。

表1 不同信號兩種去噪方法的指標對比Tab.1 Comparison of two denoising methods for different signals

3 結論

針對現有ECG 信號去噪方法的不足，本文提出基于EMD 與IMF 分量統計特性的ECG 去噪方法。本文方法首先對含噪ECG 信號進行EMD 分解得到一系列IMF 分量，然后利用IMF 分量的統計特性確定每個IMF 分量的物理意義，即確定IMF 分量屬于信號分量還是噪聲分量，最后將信號IMF 分量重構得到去噪后ECG 信號。實驗選取了“MIT-BIH Arrhythmia Database”中的104、107、200 號ECG 信號，分別疊加“MIT-BIH Noise Stress Test Database”中的基線漂移噪聲信號bw 與肌電干擾噪聲信號ma 形成含噪ECG 信號，并分別采用本方法與經驗法對含噪ECG 信號進行去噪處理。通過對兩種方法的去噪結果圖和去噪后ECG 信號SNR、MSE、AC 的對比發現，本文提出的基于EMD 與IMF 分量統計特性的ECG 去噪方法的去噪效果要優于經驗法去噪。本文實驗是將本方法應用于“MIT-BIH Arrhythmia Database”中真實的ECG 信號中，下一步將研究其在臨床ECG信號去噪中的適用性。