100 MW超臨界二氧化碳布雷頓循環發電系統熱力性能研究

代 浩，呂麗霞

（華北電力大學 控制與計算機工程學院，河北 保定 071003）

0 引言

傳統的水蒸氣朗肯循環發電系統由于受金屬材料耐溫極限制約，不易提高發電效率，具有一定局限性。超臨界二氧化碳布雷頓循環在發電上具有明顯的優勢，相比傳統發電系統，相同條件下能達到更高的發電效率[1-2]。

文獻[3]對 SCO2發電循環進行相關試驗，完成了SCO2循環發電理論的初步驗證。由于SCO2發電的優越性，越來越多的學者對其進行研究，文獻[4-5]將 SCO2循環發電運用于核能上，并將SCO2與常規的氦氣和水蒸氣循環進行對比，發現前者具有更高的循環效率。除了將SCO2發電技術應用于核能外，文獻[6]將 SCO2應用于太陽能熱發電系統中，結果表明將SCO2替代原始的熔鹽作為傳熱流體，電站將具有更高發電效率，證明了SCO2在太陽能發電技術中同樣適用。文獻[7-8]對SCO2熱力性能進行研究，通過改變不同的運行參數，得到了不同的循環效率。文獻[9-10]對 SCO2不同的循環方式進行研究，結果表明不同的循環方式有不同的循環效率，相比簡單的布雷頓循環，帶分流再壓縮與再熱再壓縮的循環使系統擁有更高的能源利用率。文獻[11]研究了再壓縮、再熱式SCO2循環，通過搭建模型探討了工質溫度和壓力對整個發電系統的影響。文獻[12]針對SCO2鍋爐受熱面的布置，通過鍋爐參數對比和熱容量分析，提出了一種新的鍋爐布置方案。文獻[13]對SCO2循環發電的壓縮機進行重點研究，包括主壓縮機、再壓縮耗功以及循環熱效率等參數，最后使用優化算法對參數進行尋優。文獻[14]對SCO2透平進行設計，在傳統透平的基礎上，采用一種新型的透平結構，并借助軟件分析其安全性以及成本，完成設計方案的選取。文獻[15]基于MATLAB軟件對 SCO2循環關鍵設備進行建模，通過仿真計算證明存在最佳分流比等參數，使系統具有最高的循環效率。文獻[16]通過構建600 MW燃煤發電仿真模型，研究了關鍵參數對發電效率的影響，并總結變化規律。

針對100 MW超臨界二氧化碳布雷頓發電系統，以分流再壓縮和再熱耦合作為循環方式，在EBSILON軟件上搭建了仿真模型，主要研究各個部件關鍵參數對系統循環效率和發電功率的影響，研究結果對SCO2發電系統的建立與運行提供相關理論依據。

1 系統模型建立

1.1 循環方式

采用再壓縮再熱的循環方式建模，通過使用EBSILON軟件搭建的100 MW超臨界二氧化碳發電循環系統如圖1所示。

圖1 100 MW超臨界二氧化碳發電系統模型Fig. 1 Model of 100 MW supercritical carbon dioxide power generation system

首先工質在鍋爐中吸熱升溫，達到相應的溫度條件，隨后進入高壓透平進行第一次做功，為了提高熱效率，完成做功的工質會再次進入鍋爐進行吸熱升溫，然后進入再熱透平進行第二次做功，此過程為再熱過程。為了避免余熱的浪費，完成兩次做功的工質會經過兩個回熱器進行換熱。工質通過低溫回熱器后將進行分流，一部分工質直接進入再壓縮機中升壓，升壓后的工質與低溫回熱器出口工質溫度將更加吻合；另一部分先進入預冷器，溫度降低后的工質在主壓縮機內升壓，隨后進入低溫回熱器中加熱，最終與再壓縮機出口工質匯合，匯合后的工質經過高溫回熱器吸收進入鍋爐中，此過程為再壓縮過程。與簡單的布雷頓循環相比，再壓縮再熱的循環方式能有效減少熱量損失，從而提高系統循環效率。

1.2 數學模型

建立數學模型，并分析系統各部件各點熱力學狀態變化，得到各個參數的數學表達式。

系統循環效率η為：

式中：Wt為透平輸出功，kJ；Wc為壓縮機耗功，kJ；Qin為輸入熱量，kJ。

針對透平和壓縮機兩個關鍵設備建模采用等熵假設，分別使用等熵膨脹和等熵壓縮原理。在透平出口處，通過使用等熵焓降法計算工質比焓等參數。由于透平入口工質溫度和壓力已知，根據CO2工質物性可計算得到此處工質的熵和比焓hin,t；再利用等熵原理，透平出口工質熵等于入口工質熵和已知的出口壓力，根據 CO2工質物性可計算出透平出口工質比焓 hout0,t；根據已知的透平效率ηt，可得到實際的透平出口工質比焓hout,t，有：

式中：qm為循環質量流量，kg/s。

在壓縮機出口處，通過使用等熵焓升法計算工質比焓等參數。由于主壓縮機入口工質溫度和壓力已知，根據CO2工質物性，可計算得到此處工質的熵和比焓hin,c；再利用等熵原理，出口工質熵等于入口工質熵和已知的出口壓力，根據 CO2工質物性可計算出壓縮機出口工質的比焓hout0,c；根據已知的壓縮機效率 ηc，最終可計算得到實際的壓縮機出口工質比焓hout,c，有：

壓縮機總耗功為：

式中：hin,hot為換熱器熱端入口焓值，J/kg；hout,hot為出口焓值；J/kg；hin,cold為冷端入口焓值；hout,cold為出口焓值，J/kg。

根據能量平衡得，輸入熱量為：

式中：hin為鍋爐處工質入口焓值，J/kg；hout為出口焓值，J/kg。

1.3 模型驗證

為了驗證所建模型的正確性，選用文獻[11]1 000 MW 超臨界二氧化碳運行參數進行仿真建模計算，將EBSILON軟件計算結果與文獻[11]進行比較驗證，仿真運行數據圖如圖2所示，相關數據對比如表1和表2所示。

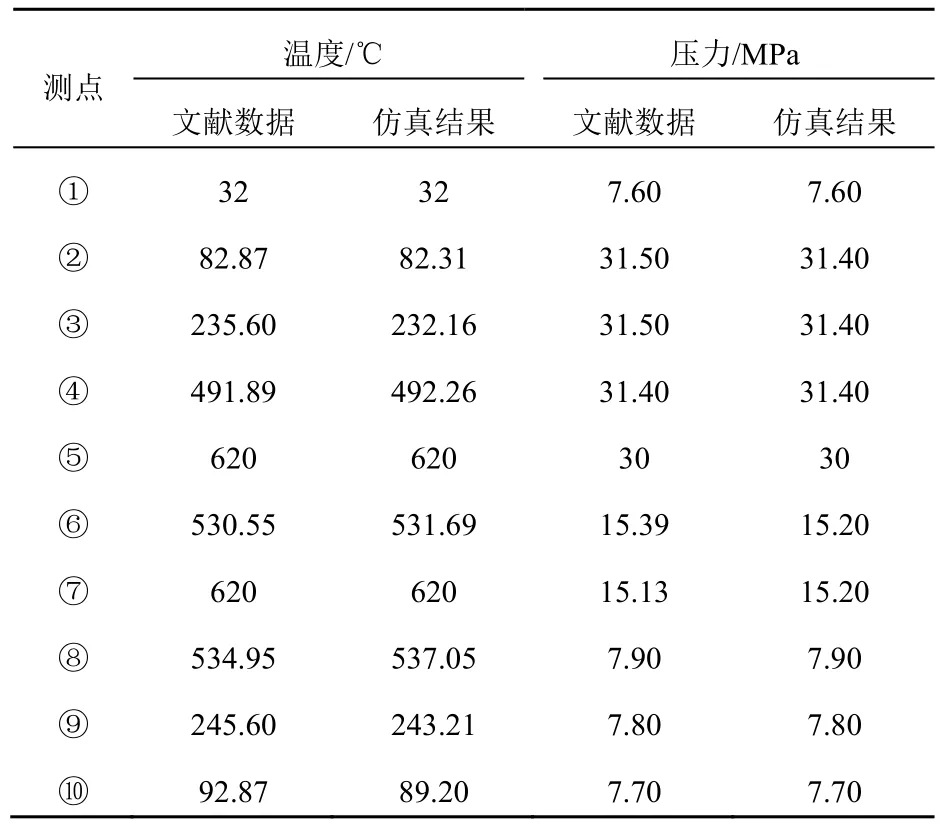
表1 仿真結果與參考文獻數值對比Tab. 1 Numerical comparison between simulation results and references

表2 主要關鍵參數對比Tab. 2 Comparison of main key parameters

圖2 仿真運行數據圖Fig. 2 Simulation operation data diagram

由仿真結果中可以看出，系統各關鍵參數接近文獻數據，具有較高的精度，驗證了使用EBSILON軟件所建模型的可靠性。

2 關鍵參數對循環效率的影響

從機理上對系統進行分析，由于透平和壓縮機相關入口參數的變化會造成工質焓值的變化，從而影響系統的做功能力以及耗功能力，最終影響循環效率。壓縮分流比會改變通過主、再壓縮機的工質流量，導致進入低溫回熱器的工質流量發生變化，造成低溫回熱器中換熱量的變化，最終影響系統的循環效率。由于影響循環熱效率因素較多，需掌握不同參數下循環熱效率及循環特性。因此，基于穩態工況下，以分流再壓縮再熱式循環系統為例，重點分析各參數對系統循環效率的影響，設計工況參數如表3所示。

表3 相關設計工況參數Tab. 3 Relevant design condition parameters

2.1 主壓縮機入口壓力

圖3和圖4為主氣/再熱溫度分別為500 ℃、550 ℃、600 ℃、650 ℃時，系統循環效率、發電功率隨主壓縮機入口壓力的變化情況。

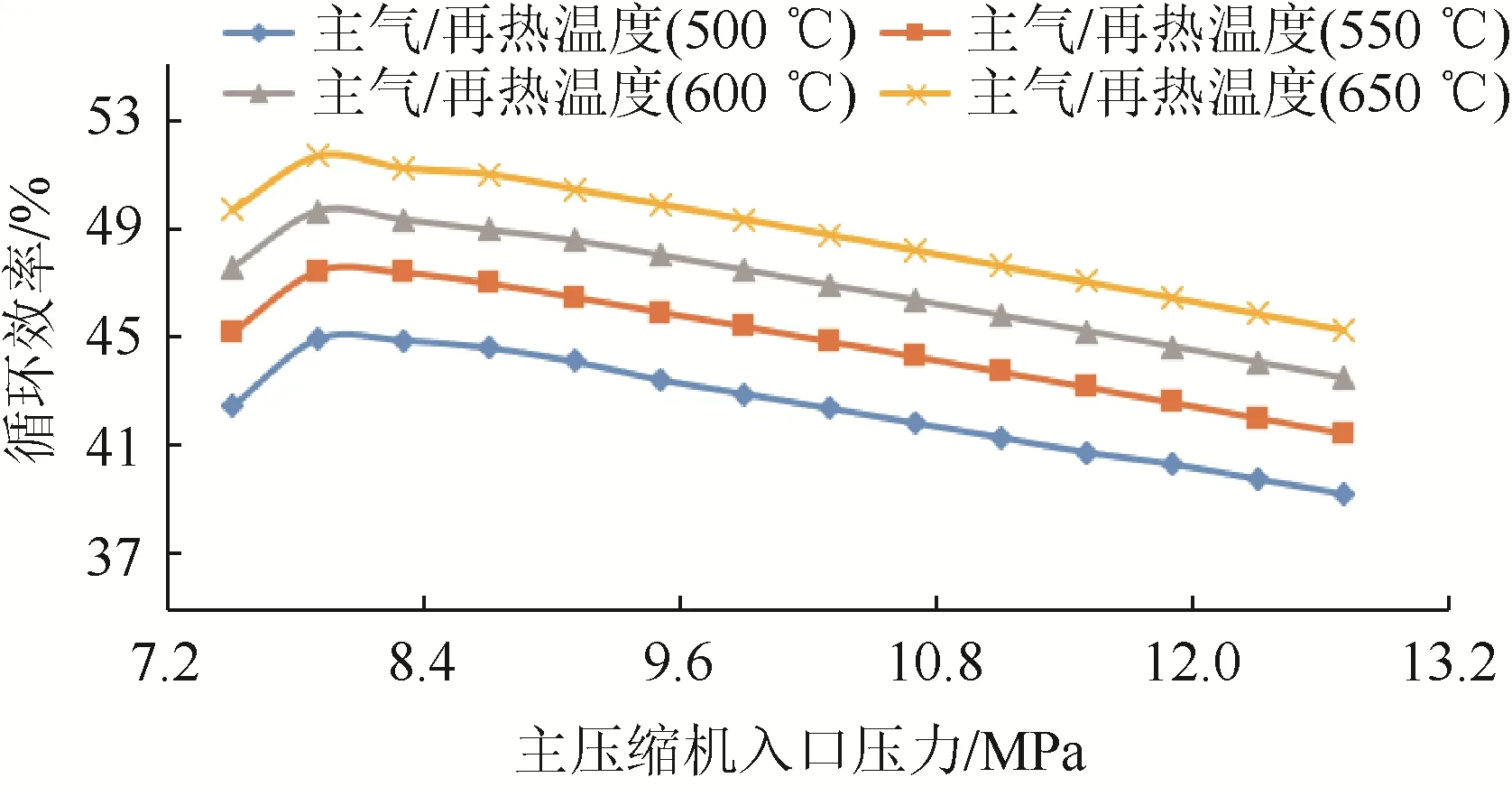
圖3 主壓縮入口壓力對循環效率的影響Fig. 3 Effect of inlet pressure of main compressor on the cycle efficiency

圖4 主壓縮入口壓力對發電功率的影響Fig. 4 Effect of inlet pressure of main compressor on the power generation

此時系統其他參數：主氣壓力30 MPa、再熱氣壓15 MPa、分流比0.3、主壓縮機入口溫度32 ℃。由圖3可以看出，在不同主氣/再熱溫度下系統循環效率變化曲線趨勢一致，當主壓縮機入口壓力小于7.9 MPa時，循環效率隨著壓力的升高而升高，當主壓縮機入口壓力大于7.9 MPa時，變化情況相反；由圖4中可以看出，在7.5～7.9 MPa范圍內，發電功率隨主壓縮機入口壓力的增加而增加，超過7.9 MPa后，發電功率隨著主壓縮機入口壓力的增加而減少。通過分析，這是由于當二氧化碳工質處于臨界壓力7.5 MPa時，其物性參數變化劇烈，適當提高壓力使換熱效率得到部分提升，從而提高系統的循環效率與發電功率；當繼續增大入口壓力，壓力會逐漸遠離臨界點壓力，二氧化碳的物性特點從變化劇烈轉變為變化平穩，提高壓力會降低循環效率以及發電功率。另外從圖中可以看出循環效率和發電功率隨著主氣/再熱溫度的升高而增加，主氣/再熱溫度與循環效率成正比，但是由于材料耐溫的限制，溫度不能無限提高。

2.2 主壓縮機出口壓力

圖5和圖6為主氣/再熱溫度分別為500 ℃、550 ℃、600 ℃、650 ℃時，系統循環效率、發電功率隨主壓縮機出口壓力的變化情況。此時系統其他參數：主壓縮機入口壓力8 MPa、再熱氣壓15 MPa、分流比0.3、主壓縮機入口溫度32 ℃。由圖 5可以看出，循環效率隨著壓縮機出口壓力的增加呈現先增加后減少的變化趨勢，當壓縮機出口壓力為34 MPa左右時，系統循環效率達到最高值；由圖6可以看出發電功率隨主壓縮機出口壓力的增加而增加，主氣/再熱溫度越高，發電功率也越高。經分析可得 3個主要因素共同決定了上述現象，分別是透平輸出功率、壓縮機耗功和熱源功率。這是由于隨著壓縮機出口壓力的增加，導致壓縮機、高壓透平、熱源三者功率升高。在前期適當提高壓縮機出口壓力，高壓透平功率的增量大于壓縮機以及熱源功率的增量之和，也就是說收益大于成本，所以循環效率顯著提高；在后期繼續提高壓縮機出口壓力，透平做功增幅有限，壓縮機耗功和熱源功率卻大幅增加，收益小于成本，從而導致循環效率下降。在壓縮機出口壓力增加過程中，透平輸出功增量始終大于壓縮機耗功增量，所以發電凈功率一直增加。

圖5 主壓縮出口壓力對循環效率的影響Fig. 5 Effect of outlet pressure of main compressor on the cycle efficiency

圖6 主壓縮出口壓力對發電功率的影響Fig. 6 Effect of outlet pressure of main compressor on the power generation

2.3 壓縮分流比

圖7為壓縮機出口壓力分別為26 MPa、30 MPa、34 MPa時，系統循環效率隨壓縮分流比的變化情況，此時系統其他參數分別為：主氣/再熱溫度600 ℃、再熱氣壓15 MPa、主壓縮機入口壓力8 MPa、主壓縮機入口溫度32 ℃。

圖7 壓縮分流比對循環效率的影響Fig. 7 Effect of compression split ratio on the cycle efficiency

由圖7可以看出，隨著分流系數的增加，系統的循環效率呈先增加后降低的趨勢，其中在0.31附近達到最高。圖8為主、再壓縮機耗功和發電功率隨分流比的變化情況，此時系統其他參數分別為：主氣/再熱溫度600 ℃、壓縮機出口壓力26 MPa、再熱氣壓15 MPa、主壓縮機入口壓力8 MPa、主壓縮機入口溫度32 ℃。

圖8 壓縮分流比對發電功率的影響Fig. 8 Effect of compression split ratio on the power generation

由圖8可以看出，隨著分流系數的增加，主壓縮耗功減少，再壓縮機耗功增加，發電功率減少。通過綜合分析，這是由于不同的分流比會影響回熱器的換熱量，從而影響系統循環效率。隨著分流系數的增加，雖然不會改變工質總流量，但是進入再壓縮機的工質流量會增加，反之主壓縮工質流量會減少，最終再壓縮機增加的的耗功量大于主壓縮減少的耗功量，進而導致發電功率降低。

2.4 再熱壓力

圖9和圖10為壓縮分流比分別為0.2、0.3、0.4時，系統循環效率、發電功率隨再熱壓力的變化情況，此時系統其他的參數分別為：主氣/再熱溫度600 ℃、主氣壓力30 MPa、主壓縮機入口壓力8 MPa、主壓縮機入口溫度32 ℃。由圖9可以看出，隨著再熱壓力的增加，系統循環效率變化曲線先上升然后下降，其中當再熱壓力為16 MPa左右時循環效率會達到最高值；由圖10可以看出，隨著再熱壓力的增加，高壓透平功率逐漸減少，再熱透平功率逐漸增加，發電功率變化曲線先上升然后下降。結合圖9、圖10進行分析，再熱壓力從10 MPa增加至16 MPa過程中，高壓透平功率減少量小于再熱透平功率增加量，從而發電功率增加，最終導致循環效率上升；再熱壓力從16 MPa增加至25 MPa過程中，高壓透平功率減少量大于再熱透平功率增加量，從而發電功率減少，最終導致循環效率下降。

圖9 再熱壓力對循環效率的影響Fig. 9 Effect of reheat pressure on the cycle efficiency

圖10 再熱壓力對發電功率的影響Fig. 10 Effect of reheat pressure on the power generation

3 關鍵參數全局優化

通過上述結果得知：多個參數對系統循環效率有較大的影響，且變化曲線呈現非單調趨勢。由于各個參數之間存在著耦合關系，為了進一步研究循環效率與多個參數之間的關系，采用遺傳算法作為優化分析方法，進行全局搜索優化，在最高循環效率下確定相關工況參數，包括主壓縮機入口壓力、主壓縮機出口壓力、分流比、再熱壓力。

3.1 建立循環效率指標

根據再熱再壓縮的循環方式以及數學模型的建立方式，計算各點的相關熱力參數：

式中：ηc1、ηc2、ηt1、ηt2分別為主壓縮機、再壓縮機、高壓透平、再熱透平的效率；qmt、qmc1、qmc2分別為流經兩個透平、主壓縮機、再壓縮機的工質流量；α為分流比；Q為鍋爐功率；W為系統凈功率；ΔT為回熱器端差；T為溫度；P為壓力；h為焓；s為熵；下標數字代表在圖2中的各個位置。

3.2 參數優化范圍

為求得系統最高的循環效率，將其作為優化目標，研究主氣/再熱溫度為600 ℃時，主壓縮機入口和出口壓力、分流比、再熱壓力這4個參數對應的最佳值，各關鍵參數的優化范圍見表4。

表4 參數優化范圍Tab. 4 Optimization range of parameters

3.3 參數優化結果

在使用遺傳算法進行優化時，首先需要完成對種群數和進化次數兩個參數的設置。雖然較大的種群數和進化次數能提高結果的正確性，但是運算時間較長。結合以上因素綜合考慮，選擇種群數為100，進化次數為1 000。全局優化結果見表5。

表5 參數優化結果Tab. 5 Optimization results of parameters

4 結論

通過使用EBSILON軟件構建了100 MW超臨界二氧化碳發電系統模型，循環方式選取再壓縮再熱式循環，通過仿真研究發現主氣/再熱溫度的增加對系統循環效率提高明顯，但是由于設備材料耐溫的限制，溫度有上限。另外主壓縮機入口壓力、主壓縮機出口壓力、分流比、再熱壓力這4個參數對系統循環效率的影響較大，且均呈現非單調變化，因此各個參數存在最佳數值使系統達到最高循環效率。由于各個參數之間存在耦合關系，所以采用遺傳算法進行全局多參數優化，最終得到了最高循環效率值，并確定了其對應的相關參數值，優化后的結果也進一步證明了分析單一參數對循環效率影響的正確性。