三角翼機翼搖滾主動控制多學科耦合數值模擬

楊起，劉偉，楊小亮，李昊

國防科技大學 空天科學學院，長沙 410072

飛行器大攻角飛行時，非定常分離和非對稱旋渦主導了周圍流場，所受氣動力/力矩具有非線性和非定常性的特點。由此，產生了包括機翼搖滾(Wing Rock)在內的多種飛行器動態穩定性問題。機翼搖滾涉及氣動、運動及控制等多門學科，影響飛行器機動能力。嚴重的搖滾問題將引起戰斗機縱向以及橫航向耦合的動態問題，使飛行器進入危險的深度尾旋狀態，嚴重威脅飛行器的飛行安全。因此，對飛行器搖滾機理和控制手段的研究是十分必要的。

針對搖滾問題，國內外進行了大量的數值模擬和試驗研究，對搖滾現象及其機理有了深入的認識[1-2]，并開展了對飛行器滾轉運動控制方法的研究。基于機翼搖滾動力學模型，采用經典理論、神經網絡、狀態觀察器等方法所設計的控制律[3-5]能有效地抑制動力學模型描述的振蕩運動。上述研究重點關注了控制算法，采用擬合的數學模型來描述飛行器的耦合效應。然而，所采用的擬合模型是對數值模擬結果的簡化，且僅將控制系統視為一個后增的設計，實際上并沒有考慮控制系統和氣動/運動的耦合作用，相關研究并不能作為評估三角翼搖滾控制系統性能的可靠手段。為了充分考慮三角翼動態運動中非線性、非定常的多學科耦合效應，提高控制系統設計精度，需要將氣動、運動和控制系統耦合計算，優化飛行器控制律。

目前，三角翼機翼搖滾氣動/運動/控制多學科耦合效應的研究尚處于初步探索階段。噴流不僅能直接提供控制力和力矩，而且能通過改變飛行器周圍流場提供間接的控制力和力矩，是一種常見的控制手段。Cummings[6]和Riou[7]等研究了前緣噴流對背風面流場的影響，發現前緣噴流可以影響主渦位置、渦破裂、二次分離渦和剪切層的相互作用。Kandil等[8]從數值上分析了采用翼面差動噴流控制三角翼搖滾的可行性，發現采用前緣非對稱噴流，可以產生相應的滾轉控制力矩。同時，受推力矢量技術的影響，1994年Helin和Watry[9]對后緣噴流展開了試驗研究，他們發現后緣噴流對外部壓力梯度進行了修正。在大迎角情況下，后緣噴流可使60°后掠三角翼非對稱渦的出現得以推遲，這有利于克服機翼搖滾現象。Nawrocki[10]研究了不同噴流方式(對稱噴流、差動噴流和矢量噴流)對前緣渦的影響，發現在大攻角的情況下，射流有控制背風面渦流的作用，能推遲渦破裂的產生。國內，王晉軍[11]、閻超[12]等也分別進行了后緣噴流的試驗和數值模擬研究。然而，上述研究都僅關注了噴流在渦流控制方面的應用，數值模擬也僅局限于Navier-Stokes(N-S)方程的求解，不涉及運動、控制領域。Kandil等[8]雖然對三角翼搖滾的噴流主動控制過程進行了數值模擬，但僅僅是將噴流作用簡化為剛體動力學方程組中的阻尼項，并未考慮噴流與動態流場的相互作用，不能精確模擬三角翼在噴流作用下的運動特性。相關的多學科耦合技術雖然被成功地應用于返回艙俯仰運動的控制方法研究中[13]，但在三角翼搖滾運動中的應用還局限于噴流對背風面渦流的影響，不涉及氣動、運動和控制的耦合效應。

控制面偏轉是另一種控制手段。前緣控制面利用背風面渦流對三角翼前緣敏感的特點[1]，通過偏轉改變前緣形狀和位置，提供一定的控制力矩。其中振蕩的前緣可視為一個渦量的非定常來源，以調控背風面的渦量[14]。Lee和Batina[15]基于錐形流假設的Euler方法，對采用前緣差動手段的滾轉控制過程進行了數值模擬，在20°攻角下實現了三角翼搖滾的有效控制。Walton和Katz[16]在風洞試驗中驗證了采用前緣襟翼差動振蕩機構控制雙三角翼搖滾的可行性：將超過 20°的滾轉振幅控制在 5°以下。Deng和Gursul[17]研究了前緣襟翼的非定常振蕩對三角翼背風面渦及渦破裂的影響，發現渦破裂位置受襟翼振幅和攻角的影響，呈遲滯變化。Boelens等[18]數值模擬了帶中心體65°后掠三角翼的自由滾轉運動。通過預先設定后緣副翼差動運動規律，研究了在馬赫數0.5、17°攻角條件下的滾轉運動特性，并比較了不同求解器的結果，驗證相關數值方法的可行性。Schütte等[19]利用求解器TAU數值模擬了帶中心體的三角翼后緣副翼差動至5°時滾轉運動情況，并與試驗結果進行了對比。此研究雖然局限于耦合方法的驗證，但展示了后緣副翼差動對背風面渦流及背風面吸力峰值的影響。此后，該研究團隊進一步通過數值模擬研究了后緣副翼開環運動(預先設定控制面運動規律)的控制效果[20-22]。李喜樂和楊永[23]進一步拓展了Boelens的工作，在數值模擬中考慮了由副翼差動產生的副翼與飛行器間縫隙的影響。目前可動部件控制手段的研究雖涉及了三角翼氣動、運動和控制的耦合作用，但多是開環控制的情況。閉環控制數值模擬中，文獻[15]雖然實現了采用前緣差動的三角翼滾轉運動閉環控制的數值模擬，但所采用的Euler方法存在不能模擬二次分離和渦破裂現象的局限性，數值模擬結果精度受限。

總之，目前采用氣動/運動/控制多學科耦合方法開展三角翼搖滾控制的研究十分少見。本文針對三角翼搖滾控制問題，基于RBF_TFI網格變形技術，通過耦合求解N-S方程、剛體滾轉動力學方程和經典控制律，對采用后緣控制面差動偏轉的搖滾主動控制過程進行了多學科耦合數值模擬，研究了控制器不同控制狀態的控制效果，為三角翼搖滾運動主動控制的多學科耦合效應研究建立基礎。

1 多學科耦合數值模擬方法

1.1 控制方程及離散方法

流場控制方程為計算坐標系下的三維非定常無量綱N-S方程(式(1))，采用無量綱單自由度Euler方程模擬三角翼滾轉運動(式(2))，并基于經典控制理論設計控制器(式(3))：

(1)

(2)

(3)

式中：φ為滾轉角；Cl_all為三角翼所受總的滾轉力矩；δ為控制面差動偏轉角；t為無量綱時間。假設控制面無厚度，控制面偏轉對質心處慣量張量無影響，因此其質心處的慣性張量Ixx不變。控制器為比例微分控制器，以滾轉角及其角速度為反饋信號，反饋控制量為控制面差動偏轉角，比例系數和微分系數分別為kP、kD。基于有限體積方法，采用二階精度的Roe格式離散對流通量。采用中心差分格式離散黏性通量。采用含雙時間步的LU-SGS方法進行時間推進求解，同時采用單邊差分時間二階精度格式離散滾轉動力學方程。通過耦合求解3個方程，實現三角翼主動控制過程的數值模擬，基本步驟如圖1 所示。

圖1 三角翼主動控制過程

1.2 動網格技術及幾何守恒律

采用剛性動網格技術實現三角翼整體滾轉運動，采用RBF_TFI網格變形方法實現控制面偏轉，結合兩種動網格技術保證三角翼滾轉及控制面偏轉時的網格質量。RBF_TFI網格變形方法結合了徑向基函數(Radius Basis Function，RBF)方法和超限插值(TransFinite Interpolation，TFI)方法的優點，是一種高效的網格變形方法[24]。其主要思路為：物面精確變形，精簡徑向基函數基點，利用徑向基函數插值方法計算網格棱線的位移，然后通過超限插值方法獲取面、體網格對應位移，從而實現整個計算域網格的變形。為避免大變形情況下出現網格交錯的情況，需根據物體變形和網格劃分情況添加基點數，提高邊界處變形后的網格質量。

網格變形會引起流動方程數值計算時間精度的降低，本文考慮了幾何守恒律[25]的影響，采取與流動方程相同的時間、空間離散方法離散GCL(Geometrically Conservative Law)方程[26]，通過DGCL(Discrete GCL)計算n+1時刻的網格體積。相關數值模擬結果證明，此方法能保持流動方程數值模擬的二階時間精度[26]。

2 三角翼單自由度滾轉運動數值模擬

采用剛性動網格技術分別對有/無后緣控制面的三角翼的自由滾轉運動進行數值模擬。將無控制面三角翼自由滾轉數值模擬的結果與文獻[1-2]進行對比，驗證本文所采用的數值方法。對比有/無控制面的三角翼數值模擬的結果，研究控制面對三角翼滾轉運動特性的影響。

帶控制面的計算模型為有厚度的80°后掠平板三角翼，控制面緊貼三角翼后緣，尺寸如圖2(a)所示。以三角翼根弦長為參考長度，則三角翼無量綱轉動慣量Ixx=0.1。而無控制面模型則沒有后緣控制面，其余參數與有控制面模型相同。以三角翼頂點為坐標原點，建立體坐標系。從三角翼后緣向頂點看去，左控制面下偏、右控制面上偏時，控制面的偏轉角為正，反之為負(圖2(b))。采用O-H結構網格離散三角翼周圍流場，流向、周向和法向分別分布201、181、75個網格點。在三角翼前緣和物面附近適當加密網格，并對三角翼控制面表面網格進行細化，壁面第1層網格法向尺度設為5×10-5倍根弦長度(圖2(c))。來流馬赫數Ma=0.3，基于根弦長的雷諾數為Re=4×104，在計算過程中三角翼基于根弦長的名義攻角不變,α=30°。

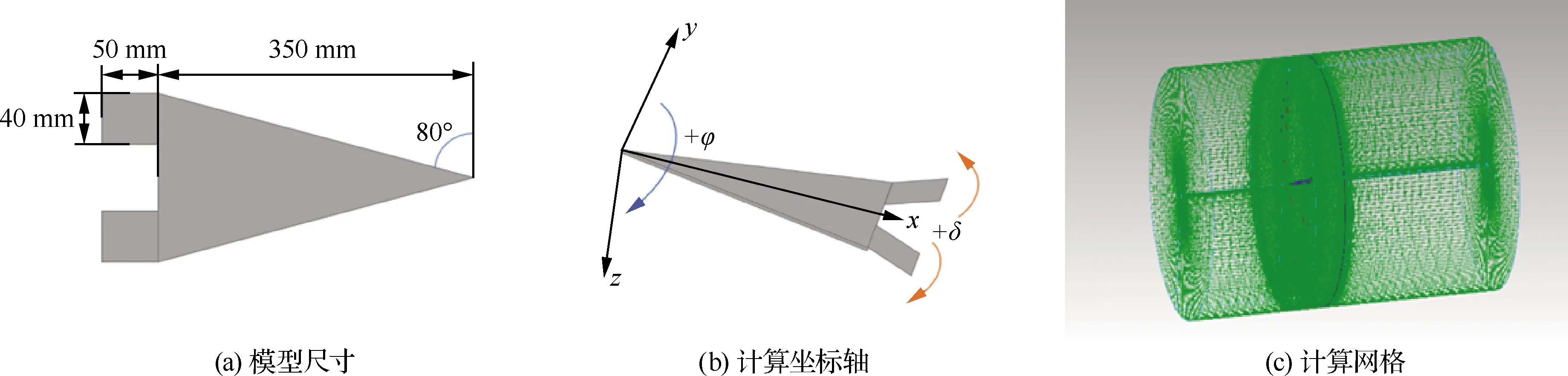
圖2 帶控制面三角翼計算模型及網格

圖3展示了兩類三角翼(是否帶有控制面)單自由度滾轉運動(控制面與翼面無相對運動)的數值模擬結果。兩類三角翼模型均產生了自激搖滾現象：無控制面三角翼模型搖滾振幅大于30°，有控制面模型搖滾振幅大于40°。位于三角翼后緣兩側的控制面增加了三角翼的受力面積，背風面非對稱渦產生了更強的滾轉力矩使得三角翼更快地失穩達到搖滾狀態，因此帶控制面模型搖滾振幅更大，振動頻率變快。國內外針對80°后掠三角翼進行了大量的單自由度搖滾試驗和數值模擬。劉偉[2]采用網格數為73×77×47(流向×周向×徑向)的網格成功模擬了三角翼單自由度自由滾轉運動，并說明此種網格密度從定性角度研究機翼受擾后的自由滾轉運動特性是可行的。在試驗方面，雖然模型加工、轉動慣量等細微差別導致搖滾振幅和頻率有所差異，但相關研究結果在定性程度上是基本吻合的，三角翼搖滾振幅大于30°。因此，本文數值模擬結果從定性上和量級上是可信的。

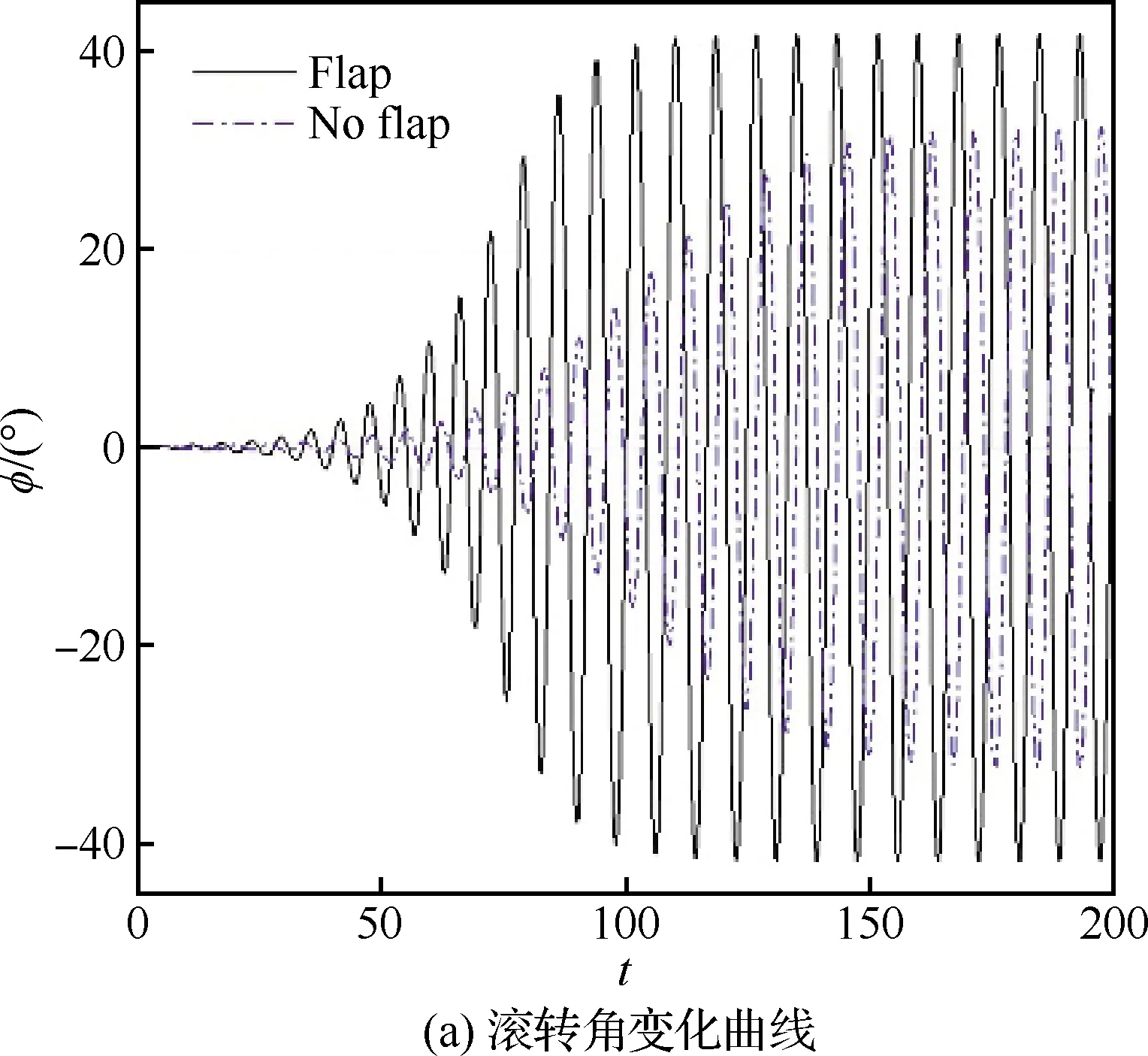
圖3 三角翼單自由度自激滾轉運動曲線

3 帶控制面三角翼閉環控制線性模型

設計控制系統需建立三角翼受控滾轉的運動模型。由于搖滾非線性問題的復雜性，同時受制于非線性動力學的發展，國內外還沒有形成對搖滾機理的一致認識[2]，無法建立精確的三角翼搖滾運動模型。一種可行的辦法是，根據數值模擬結果擬合出一個運動模型。此運動模型的精度受限，不能準確反映三角翼在控制系統作用下的運動特性，但能幫助確定控制系統參數范圍。

假設三角翼受力是其狀態參量及其一階量的函數，建立三角翼閉環控制動力學模型。三角翼滾轉時，可將控制面相對翼面的偏轉運動視為擾動，則總的滾轉力矩可分解為沒有控制面偏轉時由三角翼滾轉運動引起的滾轉力矩Cl_roll以及由控制面偏轉運動產生的滾轉力矩增量ΔCl_flap(式(4))。最終所受力矩可表示為滾轉角、滾轉角速度和控制面偏轉角、偏轉角速度的線性組合：

Cl_all=Cl_roll+ΔCl_flap

(4)

(5)

根據第2節中三角翼自由滾轉的數據，經多重回歸分析可求得參數a、b。

為了確定滾轉力矩增量與控制面偏轉角和偏轉角速度的關系，對控制面正弦差動運動(δ=δAsin(kt)，δA為控制面偏轉振幅；k為無量綱減縮頻率;t為無量綱時間)進行了數值模擬，結果如圖4所示。不同偏轉角振幅下，滾轉力矩隨控制面偏轉角遲滯變化，曲線形狀相似，大小不同。控制面振幅為30°時，控制面動態偏轉所能提供的最大滾轉力矩超過了三角翼自由滾轉最大滾轉力矩的50%。控制面動態偏轉能提供一定的控制力矩控制三角翼的滾轉運動。由多重回歸分析求得參數c、d。具體數值見表1，結合式(2)和式(3)得到三角翼閉環控制的運動模型：

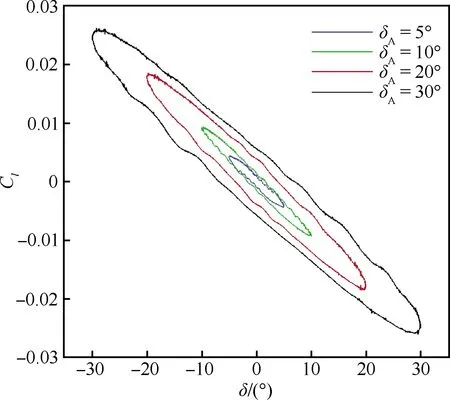
圖4 不同偏轉角振幅下滾轉力矩隨控制面偏轉角變化曲線

(6)

(7)

表1 氣動模型參數

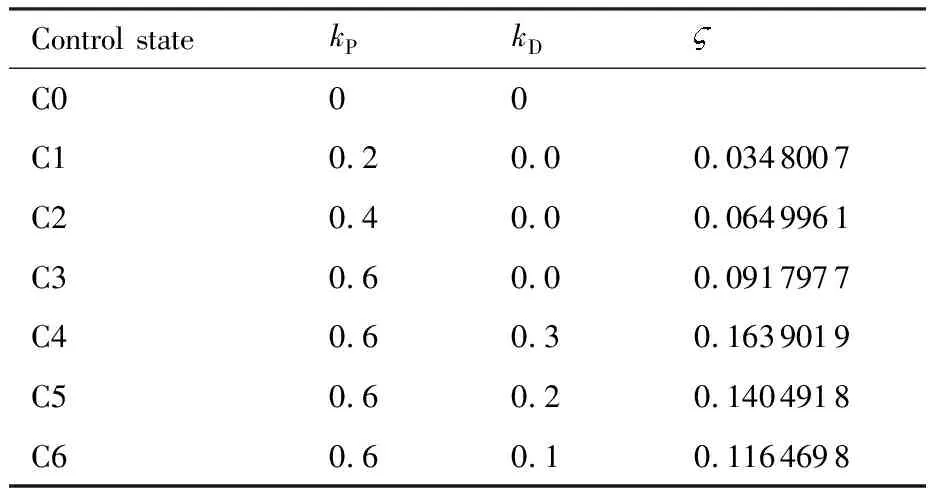
表2 不同控制狀態的控制參數和系統阻尼比

為精確分析三角翼在控制系統作用下的運動特性，需對三角翼主動控制過程進行多學科耦合數值模擬。

4 帶控制面三角翼搖滾主動控制數值模擬

基于建立的數值模擬平臺，采用不同控制參數(C1～C6控制狀態)，在極限環最大滾轉角附近啟動控制系統，對三角翼搖滾運動的主動控制過程進行多學科耦合數值模擬。采用與三角翼單自由度自激滾轉運動數值模擬相同的計算模型和計算網格。其中控制狀態C1～C3的微分系數為零，控制器為比例控制器。控制狀態C4～C6，控制器為比例微分控制器。

比例控制器作用下三角翼滾轉運動的數值模擬結果如圖5 所示。在C1～C3控制狀態下，三角翼受控后滾轉角有一定減小，并進入頻率加快的等幅振蕩狀態；后緣控制面的偏轉角也隨滾轉角的減小而減小，最終等幅振蕩。當三角翼進入穩定的等幅滾轉振蕩運動狀態后，其所受滾轉力矩與滾轉角曲線呈 “雙8”字型：在滾轉角較小時，氣流對三角翼做正功，曲線順時針變化；滾轉角較大時，氣流對三角翼做負功，曲線逆時針變化。此為典型的搖滾運動狀態。等幅振蕩運動的幅值和頻率受比例系數的影響，比例系數絕對值越大，其頻率越快，振幅越小(見表3)。同時比例系數越大，曲線越接近一條直線。在一定范圍內，比例控制器作用下后緣控制面的差動偏轉能抑制三角翼搖滾的幅值。然而，受控穩定后三角翼搖滾振幅依然較大(φmax≥30)，且搖滾頻率增加，三角翼所受到的最大氣動力矩變大，對三角翼的結構強度提出更高的要求。因此，比例控制器不能對三角翼搖滾運動產生良好的控制效果。

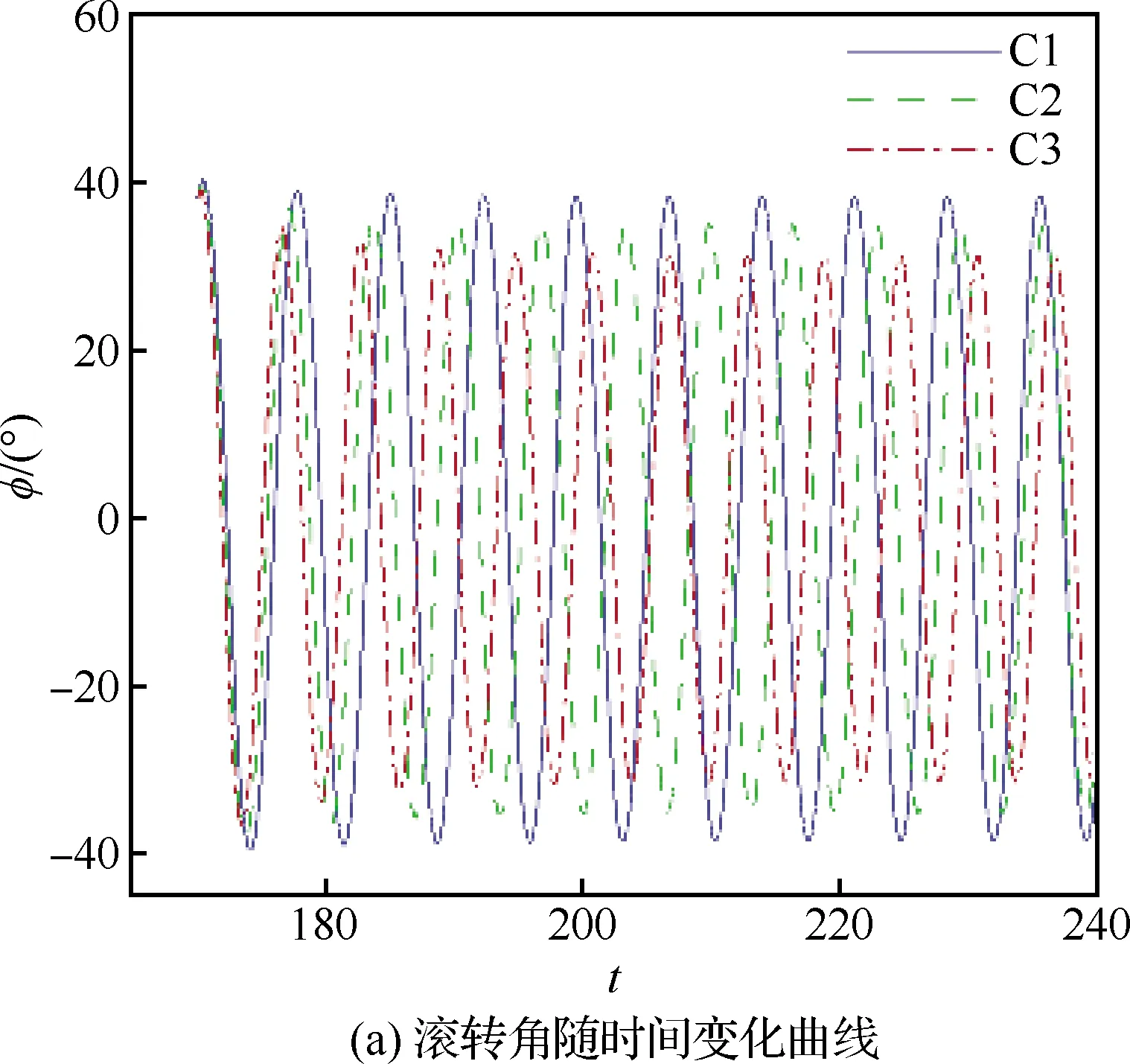
圖5 不同比例控制系數的比例控制器作用下三角翼滾轉運動數值模擬結果

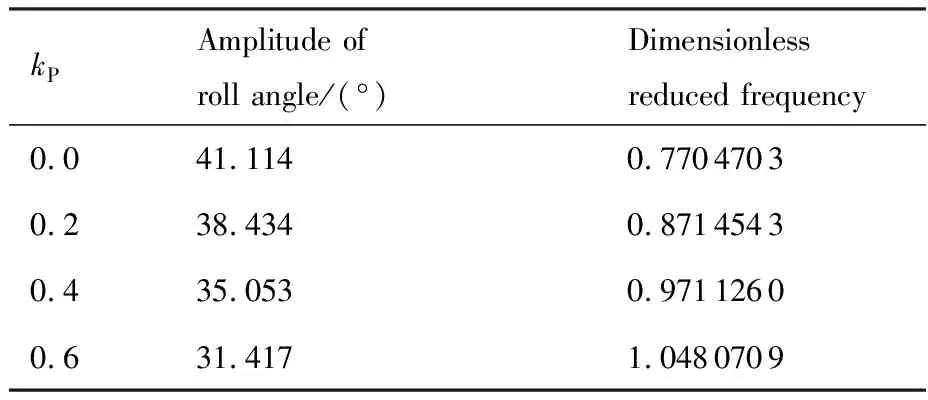
表3 不同比例系數下最終形成的極限環振幅和頻率

在控制狀態C3的基礎上，增加微分項，數值模擬比例微分控制器(C4～C6)作用下三角翼的滾轉運動，結果如圖6所示。在施加控制后，三角翼滾轉振幅逐漸減小，運動頻率逐漸減緩，后緣控制面的偏轉角隨之減小。在計算時間內，C4控制狀態下(kD=0.3)，三角翼滾轉振幅被抑制在2°內。C5控制狀態下(kD=0.2)，三角翼滾轉振幅減小至10°以內，且有進一步減小的趨勢，運動頻率降低。C6控制狀態下(kD=0.1)，三角翼進入振幅較小、頻率較低的等幅振蕩狀態。圖6(c)給出了數值模擬最后幾個周期(t>220)，不同控制狀態下三角翼滾轉力矩隨滾轉角變化曲線。C6控制狀態下，三角翼等幅振蕩，曲線呈“雙8”字，此為典型的搖滾運動狀態；但與C3相比，曲線更為接近一條直線，氣動加速、減速現象不明顯。C4、C5控制狀態下下，三角翼滾轉力矩隨滾轉角逆時針變化，氣流對三角翼做負功，三角翼滾轉運動的振幅減小，且有進一步減小的趨勢(圖6(c))。在給定范圍內，相比于比例控制器，比例微分控制器作用下后緣控制面的差動偏轉對三角翼的搖滾的抑制作用更為明顯，三角翼滾轉振幅減小，滾轉運動頻率降低。

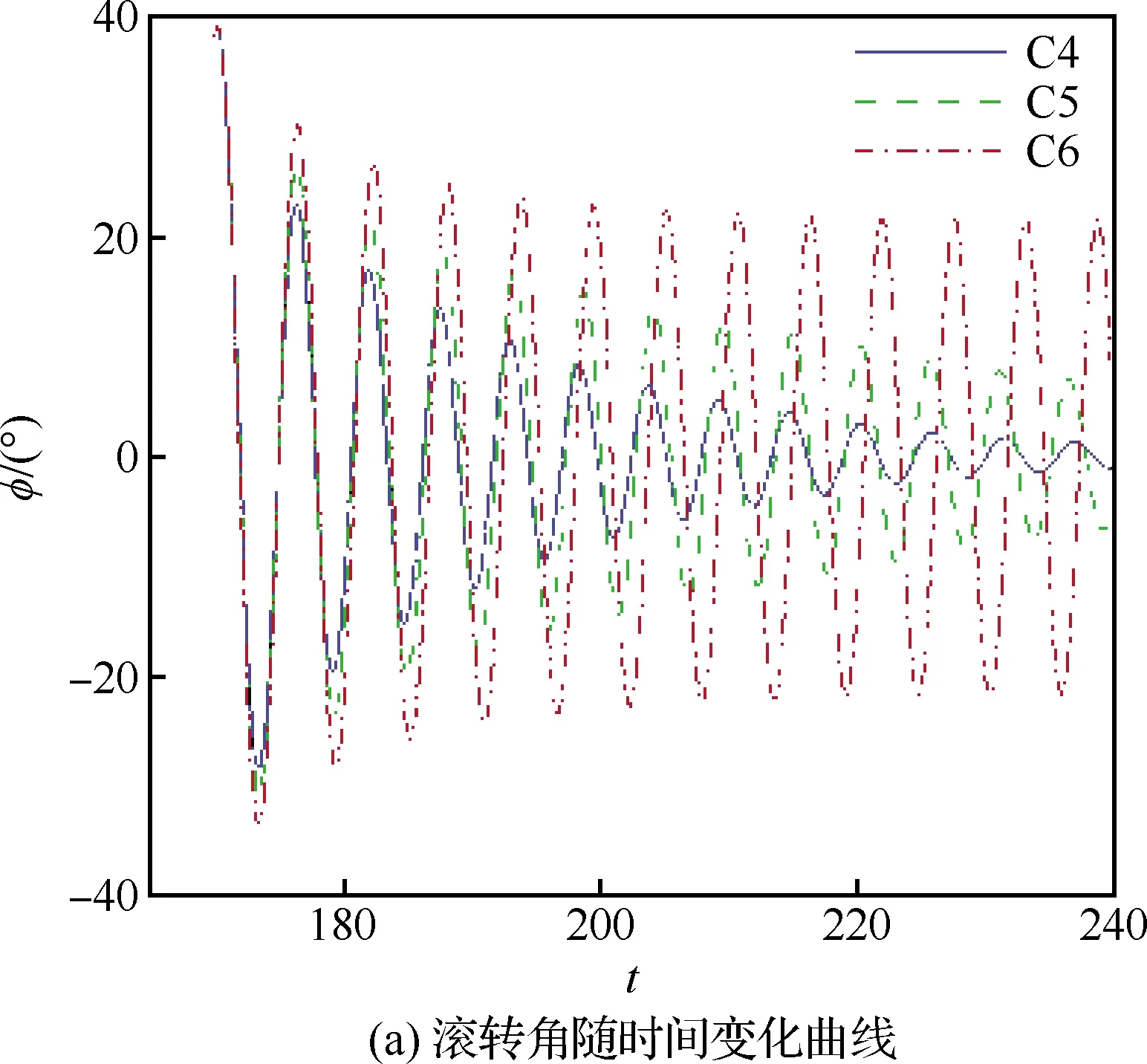
圖6 不同微分控制系數的比例微分控制器作用下三角翼滾轉運動數值模擬結果

5 控制面差動控制效果

結合三角翼流場和受力曲線進一步分析后緣控制面差動的控制效果。圖7、圖8給出了C3、C4控制器作用下，三角翼負行程(dφ/dt<0)3個 典型時刻，不同控制器作用下的流場圖，并顯示了背風面壓力分布和流向不同位置(x=0.3,x=0.7,x=1.1)壓力著色的截面流線。圖9顯示了控制作用下，三角翼控制面偏轉角、滾轉力矩隨滾轉角變化曲線(170.5≤t≤172.0)，并標明了3個典型時刻的位置。

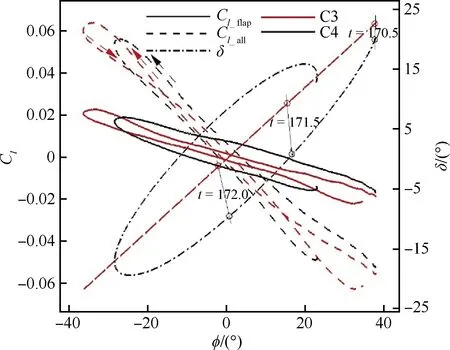
圖9 不同控制器作用下控制面偏轉角、滾轉力矩隨滾轉角變化曲線

從流場圖可以看出，控制面偏轉對前緣渦非對稱升降的影響十分小，不具備有效控制前緣渦的能力。控制面表面壓力分布既受三角翼前緣渦的影響也受控制面偏轉的影響。在三角翼滾轉角較大時(如圖7(a)、圖8(a)所示)，比例、比例微分控制器作用下三角翼后緣控制面均有較大偏轉。此時，上偏控制面形成壓縮拐角，出現局部高壓；下偏控制面雖然遠離集中渦，但由于新的渦流的形成，出現了低壓區。控制面差動運動使三角翼加速向零度滾轉角滾轉。比例控制器作用下，偏轉角隨著滾轉角線性變化，當三角翼剛轉過初始位置(φ=0°)時，控制面開始反向偏轉，但角度很小，提供的反向控制力矩較小；同時，上偏一側的翼面更為靠近前緣渦，進一步削弱了控制面提供反向控制力矩的能力(圖7(c))。此時，總的滾轉力矩隨滾轉角變化曲線存在順時針的內環，三角翼在滾轉角較小時處于加速偏轉狀態。而比例微分控制器作用下，微分項的存在使得控制面在轉到初始位置之前，就開始反向偏轉。當滾轉較小時(圖8(c))，三角翼上升一側的控制面下偏，下降一側控制面下偏，提供了一個與前緣渦升降趨勢相反的控制力矩，使得總的滾轉力矩隨滾轉角變化的零點向兩側移動，曲線順時針內環消失，對三角翼滾轉運動起到減速的效果。

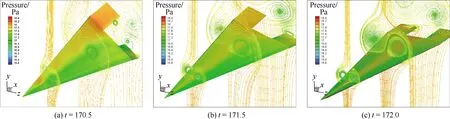
圖7 比例控制器作用下三角翼典型時刻流場圖

圖8 比例微分控制器作用下三角翼典型時刻流場圖

6 結 論

本文建立了氣動、運動、控制多學科耦合數值模擬方法，基于線性模型選擇控制器參數，模擬了三角翼搖滾運動的主動控制過程，分析了差動的后緣控制面在不同控制器作用下的控制效果。結果表明：采用比例、比例微分控制器，后緣控制面差動偏轉均能使三角翼搖滾振幅減小。其中比例控制器作用下，三角翼搖滾振幅雖有一定的減小，但減小幅度不大，且搖滾頻率有所增加。與比例控制器相比，比例微分控制器的控制效果更好：比例微分控制器作用下，控制面偏轉既能抑制三角翼的滾轉振幅又能降低三角翼的搖滾頻率。選擇合適的控制參數，三角翼的滾轉振幅能被抑制在2°以內。結合流場分析，發現后緣控制面的差動偏轉不具備有效控制三角翼前緣渦的能力。比例、比例微分控制器作用下，控制面偏轉在三角翼滾轉角較大時均會提供更強的減速滾轉力矩；而在滾轉角較小時，相比于比例控制器，比例微分控制器作用下的控制面能提供足夠大的控制力矩使得三角翼滾轉運動減速，破壞了“雙8字” 的內環特性。這是比例微分控制器控制效果更好的原因。