高等數學課程中基于GeoGebra軟件的信息化教學

李建濤

(遼寧大學 數學院，遼寧 沈陽 110036)

0 引言

高等數學，又稱微積分，是現代科學的重要基礎.高等數學課程是大學理工科學生最重要的數學基礎課，對應的數學分析課程也是數學專業學生最重要的專業基礎課之一.但是，目前高等數學課程的教學現狀不容樂觀.因為高等數學課程知識點多、難度大、理論抽象，所以很多教師在講授高等數學課程時，已經認識到高等數學里面的無限序列和極限思維是一種本質上與學生上大學前使用的思維方式完全不同的數學思維.學習高等數學，需要學生從中小學時熟悉的有限運算過渡到無限運算，從初等數學到高等數學之間進行思維轉換.高等數學中的分類、猜想、分析概括、抽象化、形式化的數學思維，讓初入大學的學生較難理解和掌握，致使很多學生學習吃力，對高等數學產生畏懼心理，學習興趣缺失.因此，就如何提高高等數學課程的教學質量，形成行之有效的教學方法，是目前高等數學教學改革的一個重要課題，而且已有很多高校教師對此進行了探索與實踐[1-5].

高等數學的思維方式的形成是一個復雜的過程，是一種循序漸進的過程，包括數學概念的表示，形象化、概括、分類、猜想、歸納、分析、抽象化、形式化等等.例如數學概念的形象化是其中一個非常重要的步驟，通過形象化和可視化的例子，幫助學生建立高等數學的數學思維很有必要.現代科學發展日新月異，計算機技術迅猛提高，使用信息化和可視化的手段輔助教學，可以讓學生更形象直觀地認識數學思維未知的關聯，從而更深刻地理解數學思想，提高學習興趣.目前，已有很多教師對高等數學的可視化教學模式的改革進行了探索[6-14]，例如用Matlab、Mathematica、GeoGebra等軟件進行可視化的設計模擬，將形式化的數學概念和問題形象化，樹立了一個值得探索和推廣的教學改革實踐范例.

本文介紹基于GeoGebra軟件進行的信息化教學改革的實踐和相關案例分析.GeoGebra是完全免費開源的數學軟件，具有強大的代數和幾何功能，與專業的Matlab、Mathematica等收費軟件相比，界面更友好，需要的預備知識更少，大多數教師和學生都能很快地上手使用.另外，GeoGebra更吸引人的一點是，可以通過滑動條工具進行動態演示一些數學過程，而且還可以通過著色工具和多角度連續的移動，更細致準確地展示相關的數學圖像.在教學過程中使用GeoGebra軟件進行教學實踐暨信息化輔助教學，可以動態化地演示高等數學教材中抽象的概念和例子，與教科書中包含的靜態圖像不同，這種動態化的演示更形象直觀地展示相關數學理論，實現了數學概念的可視化和動態演示，使學生能夠直觀地理解各種概念，有利于微積分思想的體現.配合GeoGebra的動態演示，可以提高學生對數列收斂性和無窮大的理解能力，如理解分割、近似替代、逼近、取極限等微積分學的主要思想，提高學生的空間想象力，有助于學生的數學思維從初級到高級的轉變.

1 GeoGebra軟件簡介

GeoGebra軟件是2002年美國亞特蘭大大學數學系Markus Hohenwarter教授研發的用于教學的免費開源軟件.軟件的名字是由“Geometry”(幾何)與“Algebra”(代數)組合而成.GeoGebra是一款動態幾何軟件，簡單易學，不僅能畫出靜態的平面和立體圖形，還能通過滑動條將一些數學過程動態地展示出來；并且具有強大的代數功能，可以進行各種代數運算.正如數學家Germain所說“代數不外乎符號的幾何，幾何不外乎圖形的代數”，GeoGebra軟件將代數和幾何有機地結合起來，比較完美地解決了一些數學概念的可視化.目前在國內外數學教學的各個階段，包括中小學和大學數學教學中，得到了廣泛的應用.

GeoGebra軟件主要有代數窗口和幾何窗口，結合它的代數計算能力與幾何作圖能力，允許我們對高等數學里的各種數學對象進行研究與探索.例如，通過代數方程畫出平面的、立體的圖形，并且還可以通過使用區域著色的工具，將對應的數學對象更準確、更形象地表示出來.另一方面，GeoGebra軟件中具有滑動條工具，可以動態化地演示一些數學過程，這是非常有用的.高等數學中比較難理解的就是一些極限思維，而這些極限思維通常是一種動態化的過程，例如取數列極限、定積分里的分割加細，取極限、逼近的思想.通過GeoGebra軟件的滑動條工具，可以探索圖像在某些特定作用下行為的可視化，例如可以設計極限、定積分等定義里的一些動態過程等.

GeoGebra軟件允許幾何和代數性質同時存在，在特定的空間上，實現一些動態化過程演示的可能性.例如，圖像的多角度移動、數列動態逼近、極限過程等.通過觀察點的逼近過程、定積分里分割加細過程等動態演示，可以激發學生的學習興趣，對相關問題能夠形成猜想，更容易理解相關的定義和性質.

2 動態輔助演示的教學案例

本節介紹在實際的教學實踐中，利用GeoGebra軟件進行可視化、信息化輔助教學的一些案例.這些案例涵蓋了高等數學教材中主要的數學概念，通過教師在課堂上進行動態化演示以及鼓勵學生課下利用GeoGebra軟件自己動手對數學概念進行可視化的教學實驗，促進學生對相關數學問題的理解，提高了學生的空間想象力，激發了學生的學習興趣，從而取得了良好的教學效果.

2.1 案例一：數列極限

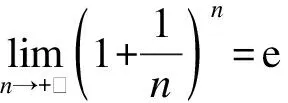
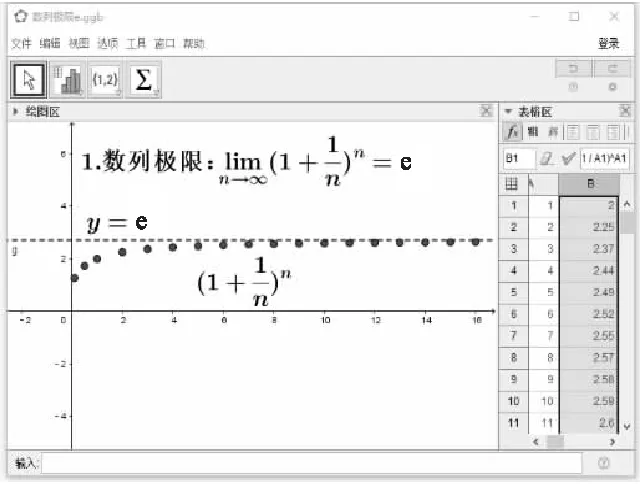
圖1 數列極限

2.2 案例二：微分與導數的概念

微分和導數是高等數學中的重要概念.函數在一點處的導數的幾何意義是函數對應的圖像在此點處的切線斜率.通過GeoGebra軟件動態演示，可以讓學生形象直觀地發現，切線實際上是圖像上兩個點確定的割線在逼近此點時的極限位置.例如圖2中橢圓形的切線，實際上是該點附近的兩點確定的割線在兩個點逼近該點時的一個極限位置.

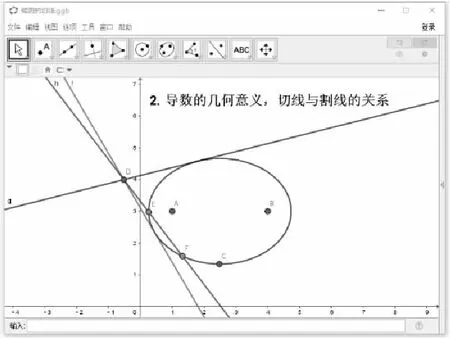
圖2 切線的幾何意義：切線與割線的關系

2.3 案例三：定積分的概念

定積分概念是微積分學中最重要的概念之一，是現代科技發展的一個重要的基礎，很多平面的數學和科學問題都是通過求解定積分解決的.定積分的思想來源于這樣的一個幾何意義，即曲邊梯形的面積.具體的過程是將曲邊梯形底邊分割成一些區間段，在每個區間段上用長方形近似替代曲邊梯形，計算面積，最后求和，取極限，得到曲邊梯形的面積，從而得到定積分的定義.使用GeoGebra軟件做圖，將積分區間進行分割，比較容易實現的就是均勻分割；分割之后，用每個區間段上的函數值上界確定的長方形面積代替真實的曲邊梯形的面積.所以整個曲邊梯形的面積近似等于這些長方形面積之和；然后將滑動條關聯成分割的數目n，移動滑動條，可以形象地展示定積分的定義中加細分割和取極限的過程.隨著滑動條的移動，設定的分割數目n的值變大，長方形面積之和就越來越接近真實面積.可以看到：圖3曲邊梯形分割成5份時，長方形面積之和還與其真實面積有較大誤差.但是圖4分割成30份時，長方形面積之和與其真實面積就相差很小了.通過這樣的動態演示，學生完全理解了定積分這個抽象定義.

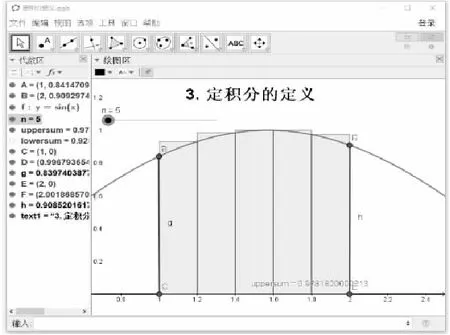
圖3 定積分的定義(n=5)

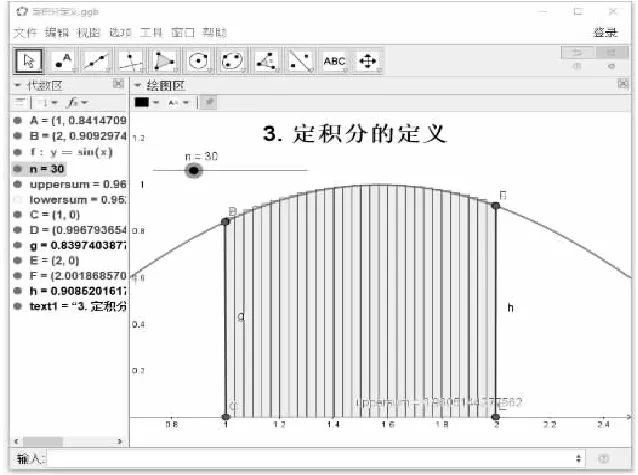
圖4 定積分的定義(n=30)

2.4 案例四：二重積分的概念

二重積分處理的是空間區域的相關計算，在現代科學技術中應用更加廣泛.二重積分來源于這樣的一個幾何意義，即曲頂柱體的體積.具體的過程是首先將曲頂柱體的底部區域進行分割，分割成一些小區域，在每個小區域上用平頂的柱體近似替代曲頂柱體，計算平頂柱體的體積，最后求和，取極限，得到曲頂柱體的體積，從而得到二重積分的定義.利用GeoGebra軟件，用類似定積分定義中的做法，將積分區域進行分割，比較容易實現的是分割成一些正方形的并集.將滑動條關聯成分割的正方形區域的個數，移動滑動條可以增加區域分塊，形象地展示二重積分里的加細分割和取極限的過程；還可以單獨或者全部展示分塊區域，讓學生能夠看到所有的細節，更加形象化；教師講解的時候也可以單獨拿出一個分塊區域，講述利用平頂柱體近似替代曲頂柱體的思想.參照下面的圖5和圖6.

圖5 二重積分定義：單獨的分塊區域

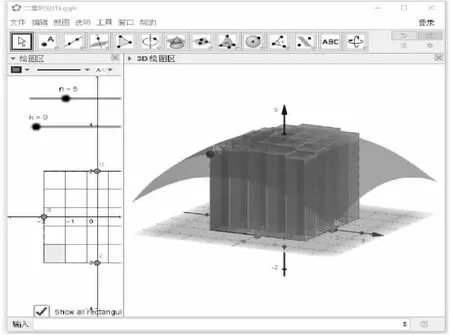
圖6 二重積分定義：展示全體分塊

2.5 案例五：復雜圖形的可視化

高等數學教材中有很多復雜的方程和空間區域，例如心形線、馬鞍面等復雜曲線和曲面，計算重積分時涉及的復雜積分區域等.空間想象力不強的學生，在學習相關內容時會十分吃力.GeoGebra軟件的幾何功能，既具有平面幾何的功能窗口，也具有立體幾何的功能窗口.利用相關的工具對這些復雜圖像進行可視化，可以開發學生空間想象能力，建立空間思維，學起相關內容時更能得心應手.例如：圖7給出了平面一個復雜心形線(x2+y2-1)3-x2y3=0的圖像，只需要在代數區域內輸入圖像的代數表達式，在幾何窗口就能顯示圖形.圖8給出了高等數學教材中常見的一個積分區域：球面與圓柱面所圍部分的空間區域.學生在計算重積分的時候經常弄錯空間區域的上下界；單純使用書本上的靜態圖像或者教師的手繪圖像，即使再細致地講解，也很難讓學生理解相關區域的細節，例如投影區域、積分上下界等.然而利用GeoGebra軟件的三維立體幾何窗口，在代數窗口輸入相關的代數方程，不僅在幾何窗口可以畫出這些復雜圖像，還能用鼠標進行移動，讓畫出的區域從多個角度進行展示，例如積分區域的投影區域、積分上下界等.學生可以從各個角度觀察區域的細節，并可以通過著色功能更細致準確地展示相關區域的細節.

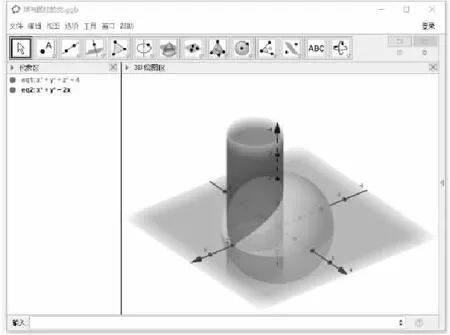
圖8 球面與圓柱面相交部分所圍區域

3 結語

本文總結高等數學課程中基于GeoGebra軟件的信息化教學改革方式.教學改革的目的是使用信息化手段研究高等數學中的一些數學概念和性質，理解高等數學中的極限思維；并利用GeoGebra軟件對一些復雜函數進行區域著色和多角度展示，實現數學的形象化和可視化，以提高教學效果.

GeoGebra這個軟件允許將代數方程和圖形表示結合起來，具有十分強大的功能.而且結合最近的網絡教學形式，我們發現GeoGebra這個軟件更適應線上線下的混合式教學.在線上線下的混合式教學過程中，通過直播更容易展示這個強大的工具，更方便讓它到達最需要的“教室”.學生可以通過直播觀察到教師使用GeoGebra軟件的所有細節，更方便學生學習和使用這個軟件.在實際的教學實踐中，學生對使用GeoGebra軟件十分感興趣，很多學生課下自己進行實驗，使用這個軟件進行畫圖，更深刻地理解了相關的數學概念和數學思想.

基于GeoGebra軟件的信息化教學是非常新鮮和有效的教學手段.通過GeoGebra軟件將數學概念可視化并作動態演示，有助于學生直觀形象地理解數學相關概念，提高他們的觀察能力和空間想象力，激發學生的學習熱情，對高等數學課程的教學改革起到了積極的促進作用；課上結合相關圖形進行教學，學生們也更深刻地理解了數學里的極限思維，提高了空間想象力，加快了從初等數學的有限空間平穩過渡到高等數學的廣維世界.