正常固結非飽和黏性土的三剪彈塑性本構模型
胡小榮,蔡曉鋒,李春博,章志榮,瞿 鵬
(南昌大學建筑工程學院,南昌 330031)
Alonso 等[1]所提出的巴塞羅那模型(BBM)為非飽和土本構模型的研究提供了一個完整的理論框架,其后Wheeler 等[2],Vaunat 等[3]在先后在其基礎上做了修正。目前,研究者們大多是基于p-q平面上的臨界狀態框架建立起適用于非飽和土的本構模型[4?6]。其中,破壞應力比M=q/p是非常關鍵的參數,一般是通過土的強度準則來確定。Mohr-Coulomb 強度準則在非飽和土中的運用非常廣泛,但該準則沒有考慮中間主應力的影響,現有真三軸試驗表明,非飽和土的力學特性很大程度上取決于中間主應力[7]。盧肇鈞等[8]、沈珠江[9]所提出的準則也存在相同問題。張常光等[10]基于雙剪統一強度理論提出了非飽和土的雙剪統一強度準則,該準則雖考慮了中間主應力的影響,但存在雙重破壞角現象[11]。Sun 等[12?13]、姚仰平等[14]基于SMP 準則研究了非飽和土的本構模型,其所采用的SMP 準則能考慮中間主應力的影響,但與雙剪統一準則相比,統一性方面則略顯不足。而三剪統一強度準則[15? 16]既保留了雙剪統一強度準則的優勢,還能反映土體強度的中間主應力效應、拉壓效應和區間效應。陳昊等[17]基于非飽和土的力學特性和三剪強度準則,將Bishop單應力變量理論與Fredlund 雙應力變量理論與三剪強度準則相結合,提出了單應力變量和雙應力變量下非飽和土的三剪強度準則,并對其做了特征分析和試驗驗證,證明了其所提準則的合理性。胡小榮等[18]在非飽和土三剪強度準則的基礎上采用等量代換法和坐標平移法推導出四個可以反映土體有效黏聚力、應力角和基質吸力影響的三剪破壞應力比。
為此,本文針對正常固結非飽和黏性土本構模型做了以下研究:
1)基于臨界狀態非飽和土力學框架,把破壞應力比替換成能反映土體飽和度影響的屈服應力和三剪破壞應力比,建立單應力變量和雙應力變量下采用等量代換法和坐標平移法的非飽和土三剪屈服函數。據此,建立了4 種不同的非飽和土三剪彈塑性本構模型。
2)確定南昌非飽和黏性土的模型試驗參數,并進行相應的常規三軸試驗,以驗證所提4 種本構模型的正確性。
3)對南昌非飽和黏性土做了真三軸數值模擬,來對比分析不同中間主應力影響系數b和基質吸力s對所提4 種本構模型的影響。
1 正常固結非飽和黏性土三剪彈塑性本構模型

1)單應力變量及雙應力變量下采用等量代換法時的屈服函數為:


將式(13)代入式(11)得矩陣形式表示的彈塑性本構關系式為:
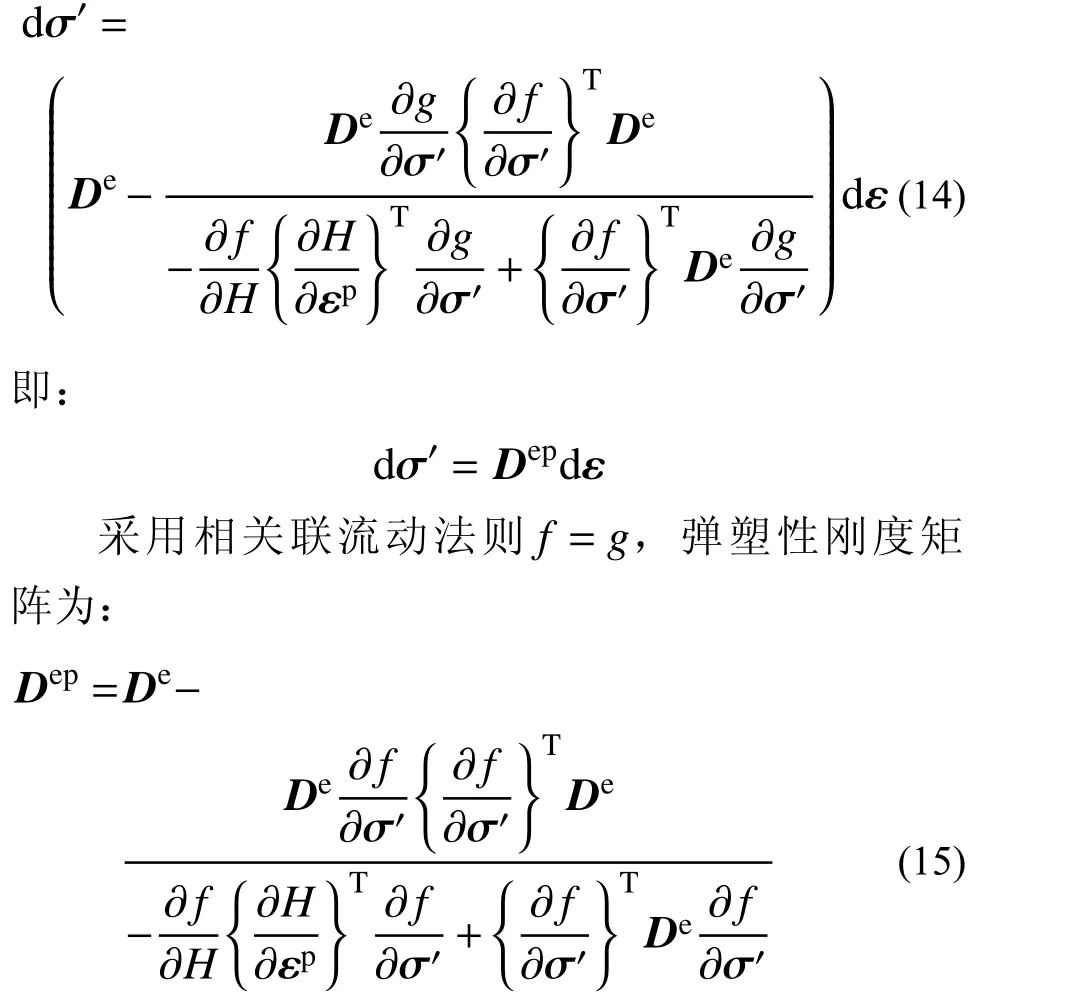
2 模型參數確定及試驗驗證
為驗證本文所提的四種非飽和土本構模型,采用南昌非飽和黏性土為試驗對象。南昌非飽和黏性土的基本物理參數為:土體比重Gs=2.75,液限wL=31.5%,塑限wP=20.3%,塑性指數IP=11.2%,最大干密度ρ=1.88 g/cm3,最優含水率w=15.4%。
2.1 模型參數確定
1)有效黏聚力、有效內摩擦角和吸力角的確定。類似于飽和土的直剪試驗與三軸試驗強度指標較為接近,采用非飽和土直剪儀對非飽和土進行直剪試驗,其強度指標與非飽和土三軸試驗也具有較好的一致性[20?22]。本文采用YS-SUDS-1 非飽和土應變控制式直剪儀,通過制作基質吸力s=0 kPa、100 kPa、200 kPa、300 kPa、400 kPa 的試樣,在法向凈壓力σ′=100 kPa、200 kPa、300 kPa、400 kPa 條件下分別做了相應的直剪試驗,得出對應的抗剪強度,并分別在法向凈應力與抗剪強度的坐標系、基質吸力和總黏聚力截距的坐標系中進行線性擬合,如圖1和圖2 所示,圖1 中基質吸力為0 kPa、100 kPa、200 kPa、300 kPa 和400 kPa時擬合優度分別為:0.99、0.97、0.98、0.98 和0.96。進而得到模型所需參數:有效黏聚力c′=27.81 kPa、有效內摩擦角φ′=27.47?以及吸力角φb=24.7?。
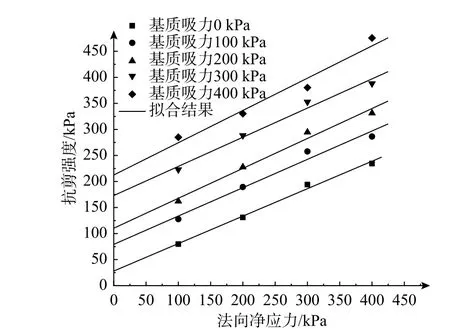
圖1 法向凈應力和抗剪強度擬合結果Fig. 1 Relationships between normal stress and shear strength

圖2 基質吸力與總黏聚力截距的關系擬合結果Fig. 2 Fitted curve of matrix suction and total cohesion intercept
2)壓縮指數λ(s)及回彈指數κ(s)確定。將土樣在不同基質吸力s=0 kPa、100 kPa、200 kPa、300 kPa、400 kPa 條件下進行壓縮回彈試驗,得出試驗數據,在e?lnp′關系中按不同s進行線性回歸處理得到對應的λ(s)和κ(s)。如表1 所示。

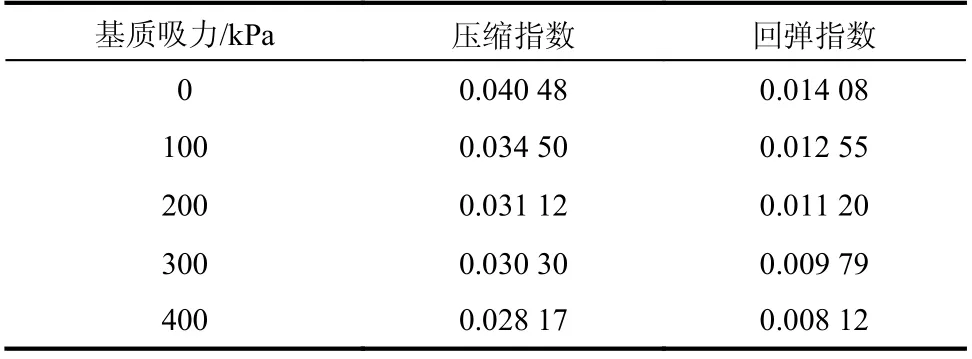
表1 不同基質吸力下的非飽和土壓縮指數及回彈指數Table 1 Compressive index and swelling index of unsaturated soils under different matrix suctions
λ(s)回歸采用如下方程確定[19]:
s?κ(s)
試驗研究表明,滿足如下線性關系:
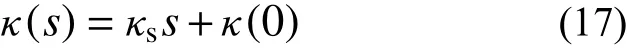
式中,κs是反映κ(s)隨著基質吸力s的變化而變化的參數。得到回歸參數κ(0)=0.014 08和κs=?1.47×105,模型參數擬合見圖3(b)。其擬合優度均大于0.95。
西雙說這還不是什么問題,大不了這三萬塊錢我不要了,可是,假如我們真的又成為夫妻,你說我是應該希望她好起來還是希望她好不起來?萬一真的出現奇跡,萬一她的病治好了,死不了了,兩個人一起面對婚后的漫長生活,怎么辦?繼續疙疙瘩瘩湊和著過?肯定不行。還得離!那么,不希望她好起來?希望她結了婚就馬上死掉?那還是一個正常人的想法嗎?那我就喪盡天良了。
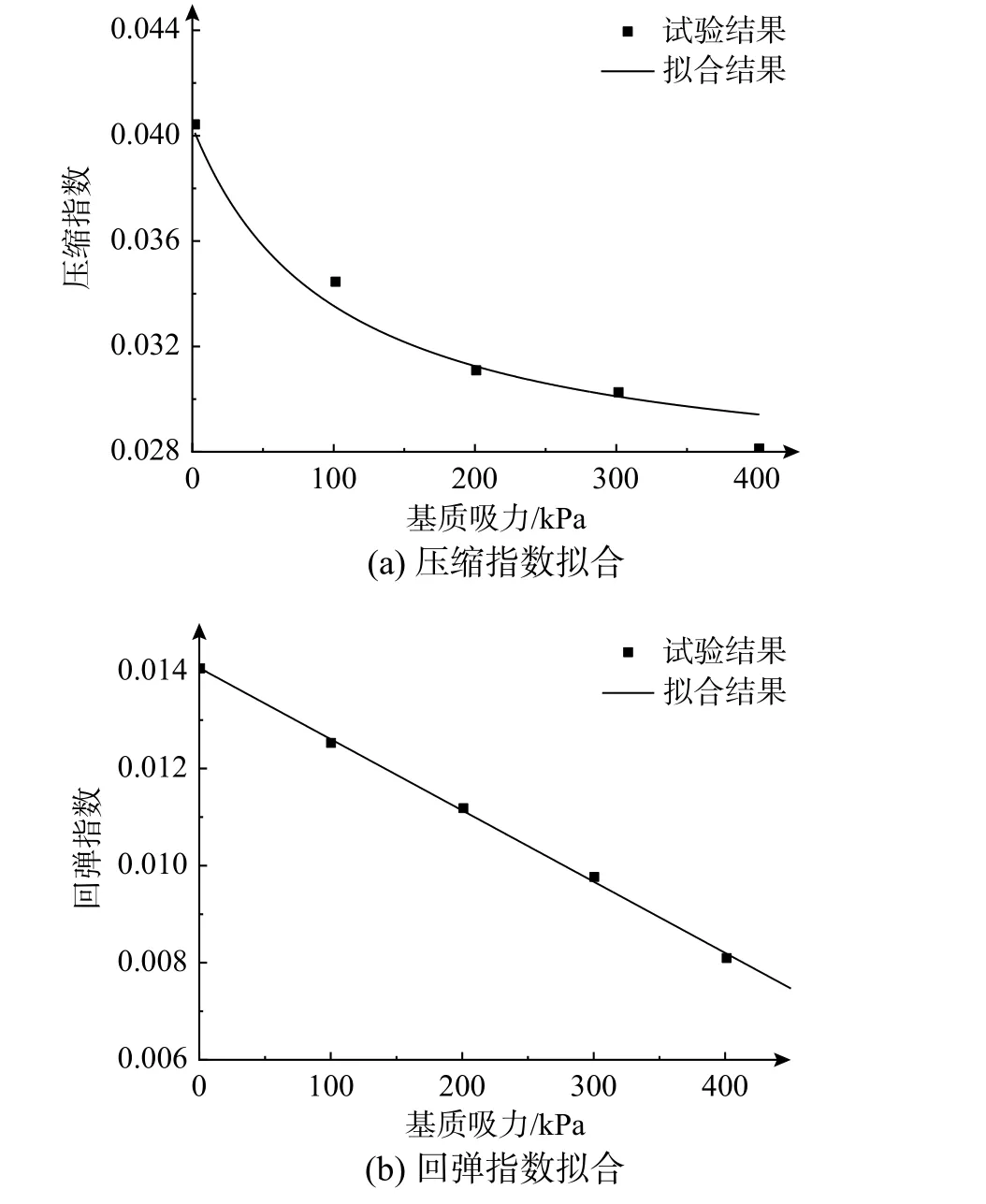
圖3 模型參數的擬合結果Fig. 3 Fitted results of model parameters
3)單應力變量法參數χ的確定。χ按文獻[23]提出的如下方法確定:
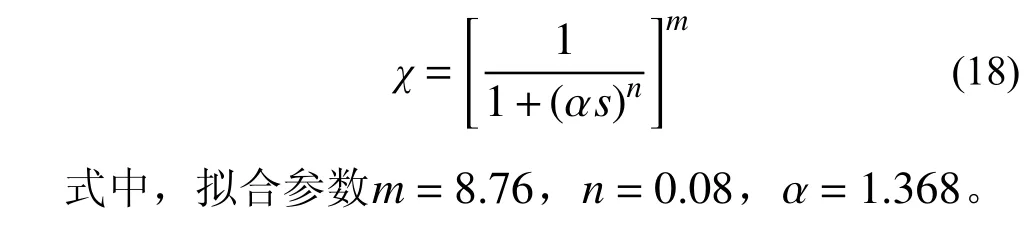
2.2 模型試驗驗證
對凈圍壓為100 kPa、200 kPa、300 kPa 及基質吸力s為0 kPa、20 kPa、50 kPa、80 kPa 條件下進行非飽和黏性土三軸固結排水試驗(Consolidation Drainage,CD),并對比了坐標平移法與等量代換法下三軸試驗的模擬值,分析非飽和土在三軸應力狀態下的應力特征。限于篇幅且結果均類似,故只列出凈圍壓分別為100 kPa、200 kPa及基質吸力分別為20 kPa、50 kPa 下的單應力變量法和雙應力變量法分別模擬土體剪應力q與軸向應變ε1、體應變εv與軸向應變ε1的關系。如圖4 和圖5 所示。

圖4 剪應力與軸向應變關系對比Fig. 4 Comparisons of q-ε1 relationship
圖4 表明,4 種模型的剪應力與軸向應變關系曲線趨勢大致相同,s不變時,采用單應力變量法和雙應力變量法時剪應力與凈圍壓成正比;凈圍壓不變時,兩種方法模擬結果曲線的剪應力與基質吸力成正比。其中,采用單應力變量法模擬相對于采用雙應力變量法模擬結果曲線偏小,雙應力變量法模擬結果更接近試驗結果,其原因是單應力變量法處理方式較為簡單,并不能像雙應力變量法較全面反映非飽和土的力學特性。采用等量代換法相比于坐標平移法模擬結果曲線要略大一些,采用雙應力變量法下坐標平移法的模擬結果曲線相較于其他模擬結果曲線更為接近試驗結果。
圖5 表明,4 種模型的體應變與軸向應變關系曲線趨勢大致相同,s不變時,采用單應力變量法和雙應力變量法時的圍壓與εv成正比;圍壓不變時,兩種方法模擬結果曲線的εv與s成正比。其中,采用單應力變量法模擬相對于采用雙應力變量法模擬結果曲線偏小,雙應力變量法模擬結果更接近試驗結果,采用等量代換法相比于坐標平移法模擬結果曲線要略大一些,采用雙應力變量法下坐標平移法的模擬結果曲線相較于其他模擬結果曲線更為接近試驗結果。

圖5 軸向應變與體應變對比Fig. 5 Comparisons of ε1-εv relationship
3 真三軸模擬及影響因素分析
在真三軸壓縮條件下,研究南昌非飽和黏性土的力學特性,除了可進行真三軸試驗外,將被常規三軸試驗驗證了的4 種本構模型應用于真三軸數值模擬及其影響因素分析也是可行的。

3.1 中間主應力影響系數b 對4 種模型的影響
在固結排水條件下,σ′2=200 kPa、σ′3=100 kPa、s=0 kPa、50 kPa、80 kPa 和b=0、0.5、1 時對比研究了不同b值對4 種模型的q-ε1和εv-ε1曲線影響。限于篇幅且對比結果均類似,故只列出s=50 kPa 的情況。圖6、圖7 分別為單應力變量法、雙應力變量法下等量代換法和坐標平移法的真三軸數值模擬對比結果。
圖6 和圖7 表明,單應力變量法和雙應力變量法下采用等量代換法和坐標平移法的模擬結果曲線均比較接近,其趨勢大致相同,尤其是qε1對比曲線非常接近。相同軸向應變ε1情況下,采用等量代換法相比于坐標平移法其剪應力和體應變均偏大。當s和ε1不變時,q、εv均與b值成正比。
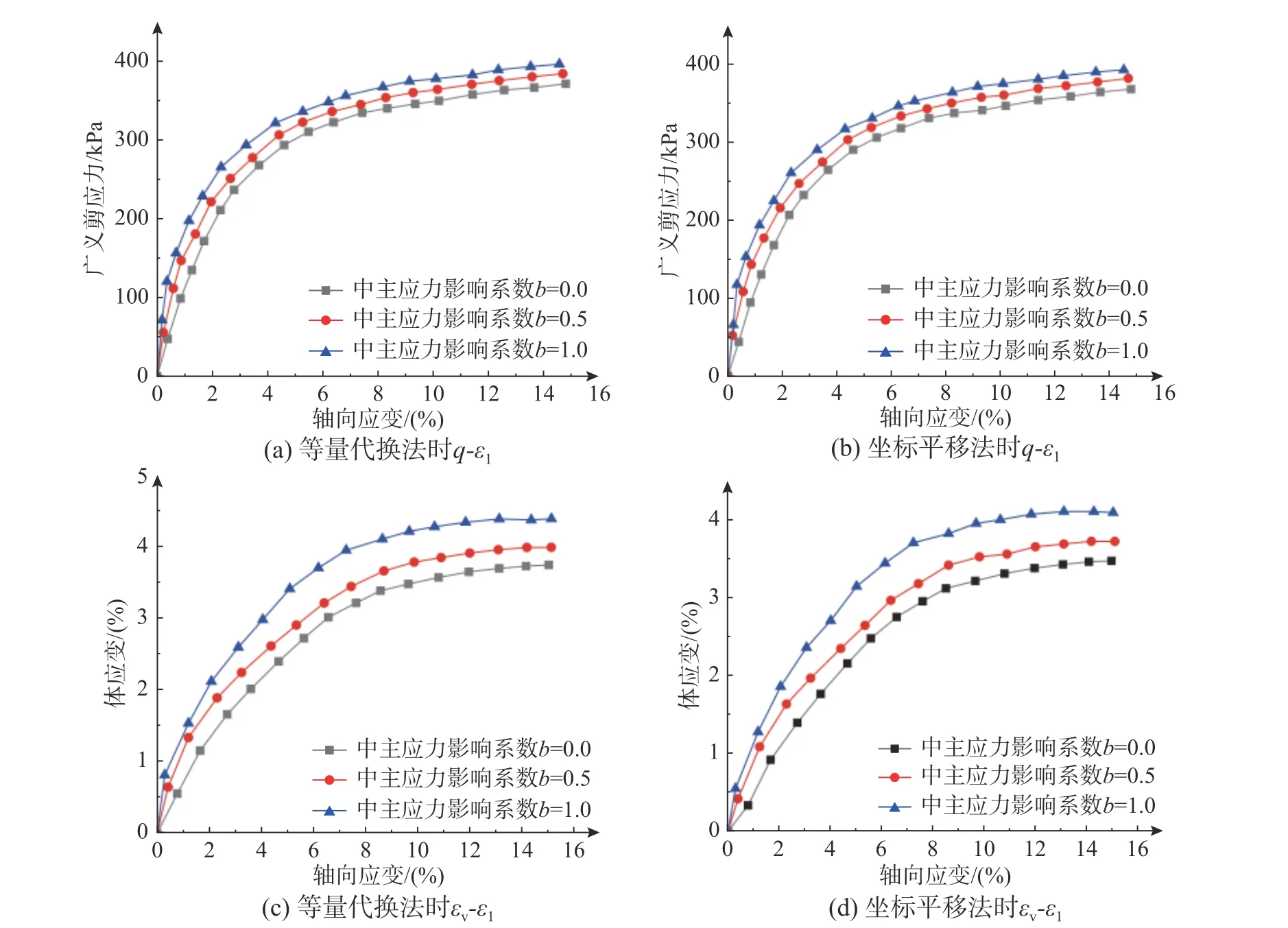
圖6 單應力變量法下基質吸力為50 kPa 時中間主應力影響曲線圖Fig. 6 Influence curves of intermediate principal stress when matrix suction is 50 kPa by single-stress variable method
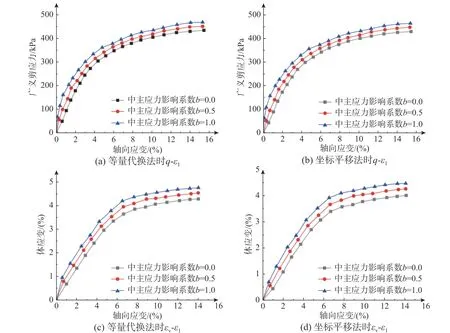
圖7 雙應力變量法下基質吸力為50 kPa 時中間主應力影響曲線圖Fig. 7 Influence curves of intermediate principal stress when matrix suction is 50 kPa by double-stress variable method
3.2 基質吸力s 對4 種模型的影響
在固結排水條件下,b=0、0.25、0.5、0.75、1、 σ′2=200 kPa、 σ′3=100 kPa 和s=0 kPa、50 kPa、80 kPa 對單應力變量和雙應力變量下采用等量代換法和坐標平移法的4 個模型分別做了真三軸數值試驗。限于篇幅且結果均類似,故只列出b=0.5時,s=0 kPa、50 kPa 下的q-ε1和εv-ε1的對比結果。如圖8 所示。

圖8 不同基質吸力下4 種模型的真三軸模擬結果Fig. 8 Comparisons of true triaxial simulated results of four constitutive models with different matrix suctions
圖8 表明,4 種模型的q-ε1和εv-ε1真三軸數值結果曲線變化趨勢均大致相同。其中,圖8(a)表明,當b值不變時,4 種模型的q均與s成正比關系。相同情況下,采用雙應力變量下坐標平移法模型的廣義剪應力較其他模型偏大。圖8(b)表明,當b值不變時,4 種模型的εv與ε1均成正比關系。ε1和b值不變時,采用雙應力變量法相對于單應力變量法的εv偏大,采用等量代換法相對于坐標平移法的εv也偏大,而s越大,εv反而相對偏小。
4 結論
在臨界狀態土力學框架下,采用非飽和土的三剪強度準則建立了4 種不同正常固結非飽和黏性土的三剪彈塑性本構模型。針對南昌非飽和黏性土確定了試驗參數、做了常規三軸試驗及真三軸數值模擬對比分析。結論如下:
(1)所建立的4 種非飽和黏性土彈塑性本構模型考慮了中間主應力影響系數b,能夠很好的反映中間主應力對非飽和黏性土的影響。此外,還能夠反映非飽和黏性土的中間主應力效應、拉壓差效應和應力區間效應。
(2)以南昌非飽和黏性土為研究對象進行非飽和黏性土的土性參數確定及其常規三軸試驗,常規三軸試驗結果表明,4 種非飽和黏性土本構模型均能較好模擬土體的應力-應變關系,還可以反映非飽和黏性土的應變硬化特性。采用雙應力變量法相對單應力變量法更接近真實試驗結果,而采用坐標平移法相對等量代換法更接近真實試驗結果。在雙應力變量法下采用坐標平移法相對其他模型更加接近真實試驗結果。
(3)真三軸數值模擬對比結果表明,隨著中間主應力影響系數增大,4 種本構模型的廣義剪應力和體應變也會隨之增大;其他條件不變時,基質吸力越大,廣義剪應力也隨之變大;采用雙應力變量法相對單應力變量法所得廣義剪應力和體應變也偏大。
附錄:

式中:L為Lame 常數;G為剪切模量。

上式各元素分別為:



