創設真實情境 培養科學思維

蔡 鉗 陳繼紅 曹衛東 周 攀 陳信余

（1.華南師范大學附屬中學，廣東 廣州 510000；2.廣州教育研究院，廣東 廣州 510062；3.廣州大學附屬中學，廣東 廣州 510006；4.廣州執信中學，廣東 廣州 510062）

情境，是教學的重要載體.物理學科的教學離不開情境.情境，也是普通高中物理課程改革中出現頻率極高的一個詞，不管是教學，還是考試，情境化是一個重要的方向.《普通高中物理課程標準（2017年）》（2020年修訂）在各章節的教學建議中均提出要創設情境進行教學，這體現了基于情境展開教學活動的重要性.

要培養科學思維，需要創設什么樣的真實情境？要如何基于真實情境展開師生活動？科學思維包括模型建構、科學推理、科學論證和質疑創新等要素.那么，情境的創設應根據課程目標的需求，有意識地指向這些要素的培養.

下面，通過理論歸納與實例展示落實科學思維素養目標的做法.

1 重視模型建構過程的師生活動

模型建構能力是應用物理學知識解決問題的重要能力，要解決實際問題，首先必須能夠從物理學的視角認識問題，進而將實際問題轉化為物理模型，然后調用物理規律解決問題.模型建構能力的培養，最重要的是要突破從現象到物理模型的思維距離（圖1）.

圖1

《思維的模式》一書將人類接觸現象的過程描述為：“重要性（指人類對事物最突出的印象）”—“表達”—“理解”3個步驟.具體到物理模型的建構，可以將這一思維過程拓展為“印象”—“描述”—“理解”—“抽象概括”—“形成模型”5個步驟.也就是說，從現象到物理模型，應該給予學生最突出的感官印象、充分的描述和表達的機會、理解的時間和空間、抽象概括的過程以及構建物理模型的結果.這樣將能夠順利突破上文所說的思維的距離.

下面，以“圓周運動”的一個教學實例展示這個思維過程.

圖2

案例1.如圖2，帶車牌自動識別系統的直桿道閘，離地面高為1m的細直桿可繞O在豎直面內勻速轉動.汽車從自動識別線AB處到達直桿處的時間為3.3s，自動識別系統的反應時間為0.3s；汽車可看成高1.6 m的長方體，其左側面底邊在a a′直線上，且O到汽車左側面的距離為0.6m，要使汽車安全通過道閘，直桿轉動的角速度至少多大？

下面通過表1展示教學活動的過程.

上述教學活動中，基于學生對物理模型建構的各個不同的思維階段，給予學生相應的啟發.整個教學過程圍繞這樣一個思路：汽車不碰到桿的直觀感受——汽車不碰到桿的物理條件——用物理模型建構一個汽車不碰到桿的圖形——應用已有的物理模型解決問題.在每一個階段，教師應給予學生充分的思維空間和時間，力求最大程度的讓學生經歷物理模型的建構過程.

值得注意的是，上述的教學過程雖然側重了模型建構能力的培養，但也涉及了分析（對汽車高度、距離以及角度大小的分析）、推理（推出桿轉動的時間、桿恰好越過汽車等結論）等思維過程.一個教學事件的發生，必然涉及學生各方面的素養，只是教師根據不同的素養目標的預設，開展側重點不同的教學活動，從而較好地落實目標.

2 重視科學推理的思維過程

科學推理是科學思維的重要體現，是科學思維的“顯性動作”.推理，包括是從一般到特殊的演繹推理、從特殊到一般的歸納推理、從類似的現象進行遷移的類比推理.下面通過教學實例探討基于真實情境進行推理的教學活動.

在探究重力做功是否跟路徑有關的問題中，在教師的引導下，某實驗小組對重力做功與路徑無關產生質疑，想從真實實驗情境中證實這個結果，于是設計了下面幾組真實實驗情境進行探究.

該小組通過表2中的3個不同情境的實驗，發現v1與v2幾乎相等，v3略小一點，但誤差范圍內v1、v2、v3可以視為相等.

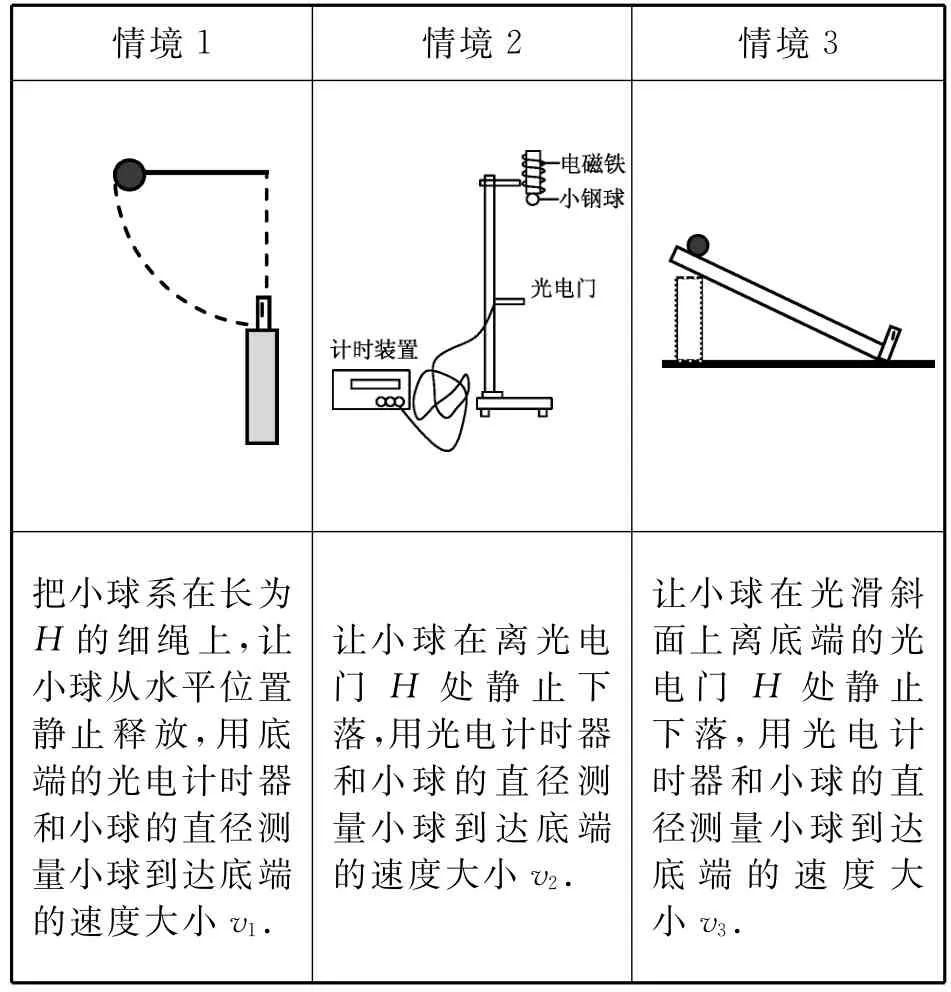
表2

教師引導學生進行推理：情境1中小球沿著圓弧路徑運動、情境2中小球沿著豎直路徑運動、情境3中小球沿著光滑斜面運動，從小球到達斜面底端的速度相等這個事實，同學的結論是什么？

學生：小球沿著3個不同的路徑到達光電門處，但路徑的高度差一樣，小球到達底端的速率也一樣.這說明這3種情況重力對小球做功的大小相等.

教師：那么，我們是否可以將這個結論進行這樣的拓展：如果小球沿著其他路徑運動，只要高度差一樣，重力做的功相等.從理論上是否能夠論證這一結論？

師生交流：如圖3，小球沿著不規則的曲線軌道下滑，下滑的豎直高度為H，重力對小球做功多大？

圖3

根據功的定義：力與沿著力方向的位移的乘積，可以輕松得到重力做功為m gH，這與前面的3個實驗的結果一致.

可以進一步探討：如圖4，將曲線軌道分為無數段無限小的軌道，每段軌道可以近似為直線軌道.第一段軌道長ΔL1，其與豎直方向夾角為θ1，根據功的定義，重力做功為mgΔL1cosθ1=mgΔH1，從而可得小球從軌道頂端下滑豎直高度為H的過程中，重力對小球做的功為W=mg（ΔH1+ΔH2+ΔH3+ΔH4+…）=mgH.

圖4

上述教學過程，通過3個真實的情境獲得3個特定的結果，在通過結果的比較演繹推理得到重力做功與路徑沒有關系的初步結論.這是在足夠多的“感性材料”的基礎上，運用推理的思維方式獲得的初步結論.接著，質疑結論的普遍性：通過這3個情境得出的結論是否能夠得出一個普遍成立的規律？于是，教師運用功的定義和公式結合數學方法進行多角度的分析，最終得到一個令學生信服的結論：重力做功與路徑無關，等于重力與高度差的乘積.

教師進而向學生提出一個更普遍的問題：是否與重力性質類似的力做功，其大小都與路徑無關？

這一過程，讓學生經歷了一個結論形成的完整的思維過程：從感性材料出發，一步步演繹、推理，結合定量分析，最終歸納得出結論，這對培養科學推理能力、落實科學思維素養目標的培養是有效的.

同樣的，上述教學不僅僅局限在科學推理這一要素，其中也涉及了質疑、論證等方面思維的啟發和培養.也就是說，任何教學過程對學生思維發展的影響都不是孤立的，而是全面的，只是教師在教學過程中側重點不同而促使教學目標指向不同.

3 重視質疑創新的問題情境

質疑是科學發展的重要動力，提出問題比解決問題更重要已經成了一種共識.在質疑的基礎上，思考、尋找解決疑問的方法，最終得到解決問題的策略，就是一種創新.下面，通過一個基于真實情境的習題的教學案例，探討培養學生質疑創新能力的一種方式.

案例2.如圖5，單人雙槳賽艇比賽中，運動員用雙槳同步劃水使賽艇沿直線運動.運動員每次動作分為劃水和空中運槳兩個階段.假設劃水和空中運槳用時均為0.8s，賽艇（含運動員、雙槳）質量為70k g，受到的阻力恒定，劃水時雙槳產生動力大小為賽艇所受阻力的2倍.某時刻雙槳剛入水時賽艇的速度大小為4m/s，緊接著運動員完成1次動作，此過程賽艇前進8m.求

圖5

（1）劃水和空中運槳兩階段賽艇的加速度大小之比；

（2）賽艇的最大速度大小和受到的恒定阻力大小.

該題的解答過程比較簡單，題目已經將賽艇的運動抽象成這樣的物理模型：劃槳時，賽艇做勻加速直線運動；空中運槳時，賽艇做勻減速直線運動.這利用動力學規律不難解答.解完這個問題，筆者覺得這么好的素材情境應該發揮更大的作用，于是向學生提出這樣一個問題：大家有沒有見過賽艇，賽艇的運動真的是這樣的嗎？我們把運動過程抽象成先勻加速、后勻減速直線運動的過程，這會不會與現實偏離太大？

問題一拋出，頓時鴉雀無聲.顯然，學生已經習慣于這樣的理想化方式，對于是否合理已經沒有思考的習慣了.當然，有個別學生說他也有這樣的疑問.

于是，筆者讓學生課后去查閱資料，下一節課再來解決問題.

最后，通過查閱資料，有學生找到對賽艇劃水比較合理的建模方式：賽艇的運動可以抽象成一個勻速直線運動疊加一個簡諧運動，它運動的速度-時間圖像大致如圖6所示.

圖6

于是教師進一步提問：賽艇的真實的速度圖像與該題中運動的v-t圖差異大嗎？

學生在圖6中作出了題目所建立模型的運動圖像的v-t圖，如圖7所示，發現兩個圖像比較接近.教師借機提出這樣的觀點：簡諧運動的圖像中，絕大部分與直線非常接近，基于高中階段的知識限制，把賽艇的簡諧運動簡化為先勻加速后勻減速直線運動的模型，是可以接受的.這樣的結論，得到多數學生的支持，還有少部分質疑的學生，他們會繼續鉆研、繼續查閱資料、繼續發現問題，這不就是教學的目的嗎？

圖7

這一教學過程，不僅能夠讓學生重新發現一個物理模型簡化思路，更能夠培養學生對習以為常的事實產生質疑的習慣，引導學生質疑之后尋找解決問題的創新的思路和方法.

4 結論

綜上所述，在創設真實情境的教學中培養科學思維，從創設情境到基于情境進行教學，每一個環節都不是孤立的，每一個環節都應該落在學生思維的關鍵點上，在最恰當的時候進行啟發，推動學生的思維順著預設的教學路徑前進.同樣，對于培養科學思維的各個要素的教學策略也不是孤立的，模型建構過程需要分析推理，分析推理過程涉及抽象概括，只是選擇的側重點不同罷了.希望上述的案例，能夠為真實情境的教學如何培養科學思維提供思路與啟發.