采用中心優化和雙尺度相似性度量的改進K-means負荷聚類方法

黃冬梅，葛書陽，胡安鐸，孫錦中，時 帥，孫 園

（1.上海電力大學電子與信息工程學院，上海 201306；2.上海電力大學電氣工程學院，上海 200090；3.上海電力大學數理學院，上海 201306）

隨著社會經濟發展和智能電網建設，電力負荷的數據量不斷增長、類型日益多樣化。大量電力負荷數據中蘊含著差異化的用電信息，然而這些信息卻不被直接利用，需要進行數據挖掘[1]。電力負荷聚類是按照負荷之間的相似度，將相似度大的負荷歸為同一類，從而得到不同類別的電力使用情況和典型用電模式，進而有效識別不同的用電規律和負荷特性。電力負荷聚類可以應用于電價劃分與制定、負荷預測、負荷模型建立、電能質量檢測等多種場合[2]。

電力負荷曲線聚類領域中應用較廣的算法有K-means算法、具有噪聲的基于密度的聚類DB-SCAN（density-based spatial clustering of applications with noise）算法、模糊C均值FCM（fuzzy C-means）算法等[3]。其中，K-means等劃分聚類算法具有可解釋度強、時間復雜度低的優點，作為基本算法被廣泛應用，但是在處理大量負荷數據時，最優聚類數目需要人為給定，每次運行隨機初始化不同的中心容易使算法收斂異常，影響聚類穩定性和質量，此外，采用歐氏距離作為相似性度量時，容易忽略負荷變化信息，導致聚類不準確等問題。

針對上述缺陷，文獻[4]通過對中心點篩選融合后使用層次K-means算法聚類，在一定程度上解決初始聚類中心的選取問題。文獻[5-6]利用遺傳算法等啟發式算法初始化聚類中心來優化劃分聚類算法，但由于使用了啟發式算法，存在耗時增大的問題。文獻[7]利用密度峰值法自動確定了聚類數目和初始聚類中心，避免人為選取聚類數目，優化了K-means聚類的效果。文獻[8]利用自定義的指標函數與粒子群優化PSO（particle swarm optimization）算法自動確定聚類數目和聚類中心。文獻[9]利用分位數和差分的思想，對負荷曲線進行形態離散化，并自定義相似性度量對負荷進行聚類分析。文獻[10]引入免疫濃度機制、變異機制，改進K-means算法對初始中心敏感的問題。文獻[11]采用非線性映射的方法，把數據映射到高維空間，從而加大數據的可分離性。文獻[12]利用6個負荷特性指標對曲線進行特征提取，并利用德爾菲法對特征的歐氏距離加權，然后進行聚類，方法提升了效率和聚類質量。

現有文獻大多通過降維和確定初始中心來提升算法的聚類效果，而在相似性度量方面采用歐氏距離作為相似度的判據，但歐氏距離只計及曲線數值距離忽略了曲線趨勢的判別。通過改進相似性度量方法，也可以有效提升聚類效果[13-15]。現有對負荷序列的相似性度量方法中，動態時間規整DTW（dynamic time warping）距離的聚類效果較好，其允許負荷序列時間維度不一致，通過彎曲時間軸來對序列中不同時間點的負荷進行匹配，在形態聚類方面有一定的優異性，但對時間軸過度規整可能會降低相似性判別的準確度，使得聚類效果不佳。此外，DTW距離的計算量較大，往往會降低聚類的效率[16-17]。

鑒于初始中心影響聚類效果和歐氏距離難以有效度量負荷趨勢的相似性的問題，本文結合局部密度和差分提取的思想，提出一種采用中心優化和雙尺度相似性度量的改進K-means負荷聚類方法。首先，利用局部密度思想來獲得負荷曲線的初始中心；然后使用一階差分向量來提取曲線的趨勢特征；最后把兩者的歐氏距離組合作為新的相似性度量，利用K-means算法使用此度量方式開展聚類分析。與傳統K-means聚類算法相比，本文方法能夠有效分辨負荷曲線趨勢之間的相似性，較為準確地識別電力用戶用電模式。

1 利用局部密度優化初始中心

在劃分聚類算法中，初始聚類中心的隨機選取極大地影響了聚類結果[18]。針對這個問題，本文利用局部密度思想對初始中心進行優化。

（1）定義負荷曲線間鄰近元素的平均距離mdist為

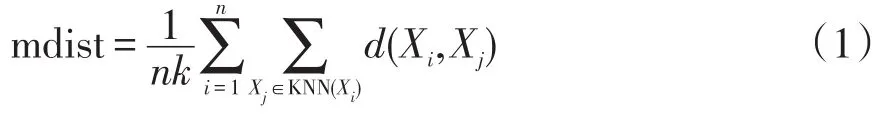
式中：Xi和Xj分別為第i條和第j條負荷曲線；d(Xi,Xj)為兩個負荷曲線之間的歐氏距離；KNN(Xi)為第i個數據最近的k個元素組成的區域；n為負荷曲線樣本的個數。

（2）定義負荷曲線的局部密度。以任一負荷曲線Xc為例，與Xc的歐氏距離小于鄰近平均距離的負荷曲線的數量定義為局部密度參數，記為ρ(mdist,Xc)，其表達式為

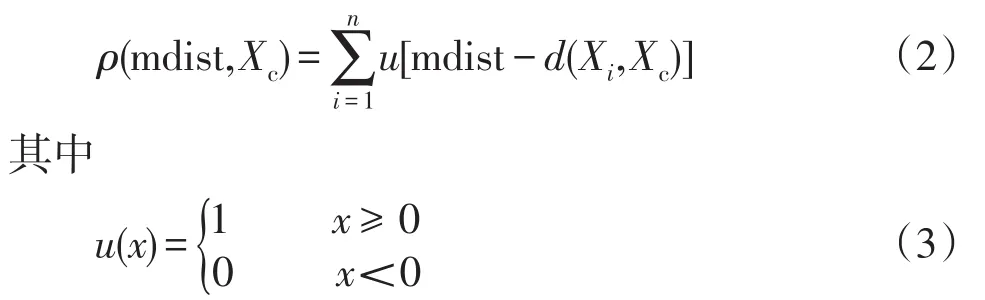
式中，u(x)為負荷曲線局部密度的更新量。ρ(mdist,Xc)越大表示該曲線的局部密度越大，作為聚類中心的概率越大。mdist表示對曲線Xc密度計算的限定范圍，若Xi和Xc的歐式距離超出mdist限定的范圍，則Xi不參與Xc的密度計算。

本文選取ρ(mdist,Xc)降序排列的前K個值對應的負荷曲線作為聚類的K個初始中心。

2 相似性距離度量

負荷聚類主要依據負荷之間的相似性將大量無序、無規則的負荷樣本劃分為多個類。因此，選取合適的相似性度量方式是負荷聚類是否準確的關鍵環節之一。

2.1 歐氏距離

對于兩條負荷序列曲線W=(w1,w2,…,wm)和V=(v1,v2,…,vm)，若用 Minkowski距離DMinkowski來度量，則有

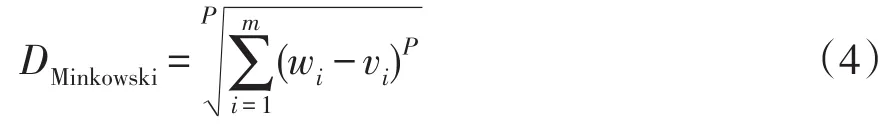
式中：m為負荷曲線的維度；P為距離系數，當P為不同值時，DMinkowski表示不同距離；當P=2時為歐氏距離，此時DMinkowski記為Deu。

2.2 差分提取

歐氏距離為兩組序列對應位置的空間數值距離，在負荷趨勢的相似性判斷中效果欠佳，而差分向量能夠反映負荷曲線在各個等間隔時間段內的上升、下降等變化信息。因此，對于m維度的負荷曲線W=(w1,w2,…,wm)，本文利用一階差分向量，將其轉換為m-1維的負荷趨勢序列，用來描述曲線的局部動態特性。

一階差分運算定義為

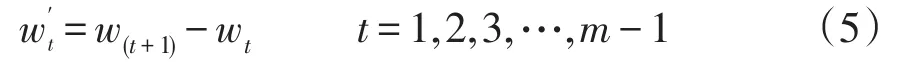
2.3 雙尺度相似性度量

本文綜合考慮負荷序列的數值特征與趨勢特征兩個因素，采用負荷數據歐氏距離和負荷差分向量的歐氏距離作為綜合相似性判據，代替歐氏距離來衡量曲線之間的相似性，兼顧距離和趨勢兩種特征。

雙尺度相似性距離的衡量方法可表示為

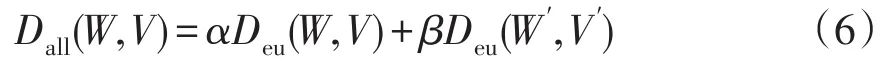
式中：Deu(W,V)為曲線W、V之間的歐氏距離；Deu(W′,V′)為式（5）所示的兩個差分序列之間的歐式距離；Dall(W,V)為曲線W、V的雙尺度相似性距離，Dall(W,V)越小表示兩條曲線的距離越近，相似度越高；α和β分別為歐氏距離和差分歐式距離所占的權重。

3 改進的K-means負荷聚類方法

3.1 改進K-mean方法

K-means聚類以原始負荷數據的歐氏距離來衡量兩序列之間的相似性，但原始數據的歐氏距離在衡量趨勢相似性方面存在一定的局限[19-20]。由于差分向量可反映負荷曲線在各個等間隔時間段內的負荷變化信息，本文采用差分向量度量負荷趨勢變化，并綜合考慮負荷歐氏距離與負荷差分向量的歐式距離，以雙尺度相似性距離度量Dall代替負荷數據間的歐氏距離作為K-means的相似性度量來衡量負荷總體的相似性，對K-means算法進行改進。

3.2 聚類評價指標

聚類評價主要是從緊密性、離散性等角度使用某些性能指標來對實驗中不同算法的聚類效果進行判斷和評價[21]。考慮到戴維森堡丁指數DBI（Davies-Bouldin index）和輪廓系數SIL（silhouette coefficient）變化范圍小，容易進行判斷，相比其他指標更適合于負荷聚類質量評判，因此本文選取DBI和SIL兩個指標來評判聚類質量。

DBI指標表示每個簇和其最相似簇之間的平均相似度，其中相似度通過簇內距離與簇間距離的比值來表示。DBI的最小值為0，DBI越小表示聚類效果越好[22]。具體計算公式為

“不要急，先聽我說完。在現實里，男主人公不是帶著兩個疑問黯然離去嗎？在現實結束的地方正是小說的開端，這也是小說家的用武之地。S返回果城，跟蹤監控那個情敵。有大半年，他一無所獲，他看到的全是其夫唱婦隨的恩愛鏡頭。S涌起了對前妻的刻骨思念，又為她被‘霸占’而火冒三丈。功夫不負有心人，S終于拍攝到了情敵出軌的鏡頭，S激動得渾身顫栗，想起了昔日看著那個女人掏出那個大牛皮信封的情景。就要一報還一報了。S曾猜想那沓照片肯定跟那個男人有關，只是苦于沒有真憑實據，也沒有蛛絲馬跡。”

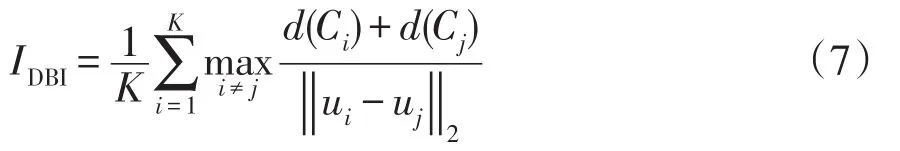
式中：IDBI為DBI指標的值；Ci為第i個簇；d(Ci)為Ci類內樣本間的平均距離；ui為第i個聚類中心；‖ui-uj‖2為第i類中心與第j類中心數據點的分散程度；K為聚類數。

樣本SIL指標表示單個數據聚類效果，其取值范圍為[-1，1]，若SIL越接近1則表示聚類效果越好，SIL為負值則表示聚類幾乎無效。具體計算公式為

式中：ISIL為樣本SIL指標的值；bi為第i個樣本到其非同類簇的所有樣本的平均距離的最小值，反映非同類簇之間的離散度；ai為第i個樣本所在簇的平均距離，反映同類簇內的緊密度[23]。

所有樣本的平均輪廓系數ISILmean可表示為

式中：ISILmean為評估聚類的總體質量；n為負荷曲線樣本個數。

3.3 算法實現步驟

改進的K-means算法包含負荷數據預處理、確定算法的聚類中心及聚類分析3個部分，其流程如圖1所示，其中，輸入為原始負荷數據、聚類數K、權重、鄰近參數個數、最大迭代次數；輸出為聚類結果。具體流程描述如下。

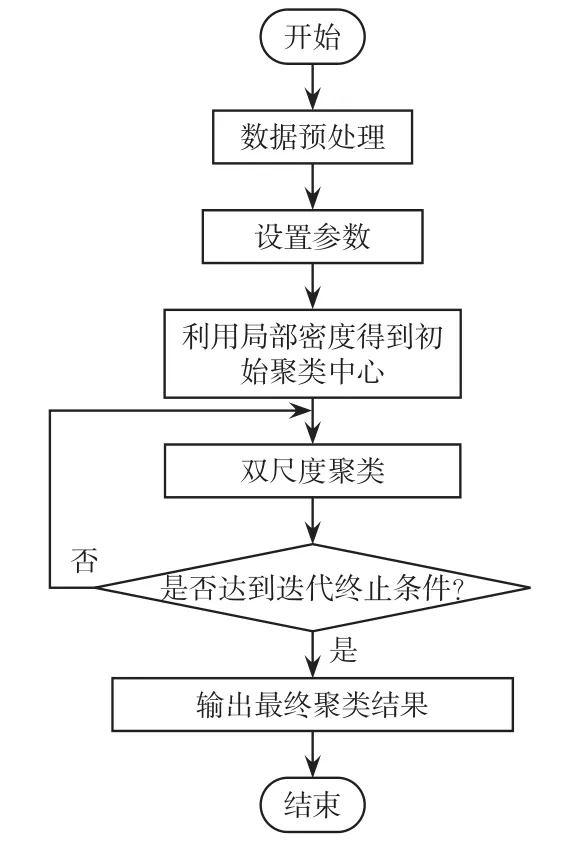
圖1 改進的K-means負荷聚類方法流程Fig.1 Flow chart of improved K-means load clustering method

步驟1數據預處理。首先對聚類的曲線進行插值補全，之后對完整數據進行極值歸一化操作。具體計算公式為

步驟3利用第1節提出的局部密度方法獲得前K個最大局部密度值對應的負荷曲線作為算法的初始中心。

步驟4相似度判定。用歐氏距離和差分歐式距離組成的雙尺度相似性度量Dall作為距離度量，計算每條曲線與K個中心的相似度，并將每條負荷曲線與相似性最大（距離度量Dall最小）的中心分為一類。

步驟5計算各類的樣本均值作為新的中心點和本次迭代的類內離散度。計算公式分別為

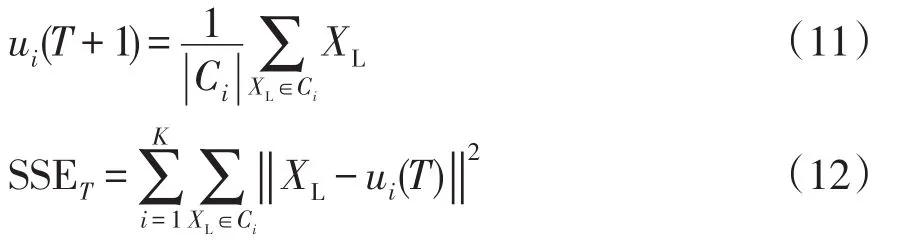
式中：SSET為第T次迭代的簇內誤差平方和SSE（within-cluster sum of squared errors）；|Ci|為簇內曲線的數量；XL為簇Ci的負荷曲線；T為迭代次數。

步驟6若滿足以下任意一個條件時，輸出聚類結果，否則以新得到的點作為中心重新執行步驟4。條件包括：①兩次迭代得到的中心點不再變化；②兩次迭代的SSE滿足 |SSET+1-SSET|＜ε，其中ε為收斂閾值；③達到最大迭代次數。

4 算例分析

4.1 算例設計

以中國南方某市1 156個用戶的日負荷曲線為實驗對象，日負荷曲線采樣頻率為1 h，即每條負荷曲線由24個功率點組成。為了驗證本文方法的有效性，利用上述數據分別運用傳統K-means算法、雙尺度K-means算法、中心優化的K-means、中心優化的DTW-K-means算法和本文算法進行聚類，對聚類結果和質量進行分析。

圖2為10次運行K-means算法的SIL指標變化，可以看出，K-means算法隨機初始中心帶來了不穩定問題，而優化后的算法由于給定了初始中心，所以只執行一次。因此本文對K-means算法及雙尺度K-means算法重復運行10次，取其中較好的結果用于對比實驗。聚類結果通過直觀的最優聚類數目下的聚類類別圖來反映；聚類質量則通過選用本文所選用的評判指標（DBI和SIL）來反映。在本算例中，為了反映負荷歐式距離和差分歐式距離權重對聚類效果的影響，設計了不同權重配比的聚類實驗，以優選權重配比。對于鄰近參數，本文根據密度峰值法的思想，選取了數據總量的2%作為鄰近元素的數量。算例的編程語言為Python，框架為scikit-learn。

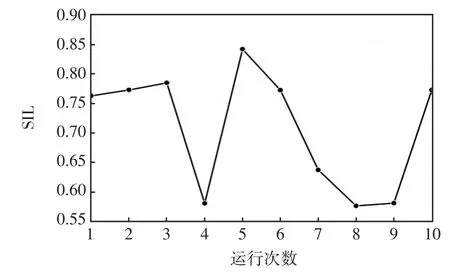
圖2 10次K-means的SIL指標Fig.2 SIL index of K-means repeated for 10 times

4.2 聚類實驗結果分析

如圖3所示，通過觀察不同聚類數目下DBI指標變化曲線，可以發現算法在K=5時有明顯的極小值拐點。圖4為基于T-sne的可視化圖像，可見，數據大致可以區分為5個區域，且區域間距離大，區域內距離小，所以本算例的最佳聚類數取為5。

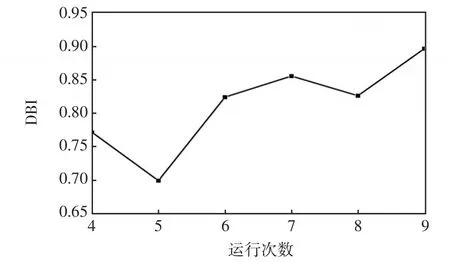
圖3 不同聚類數下DBI指標Fig.3 DBI index under different cluster numbers

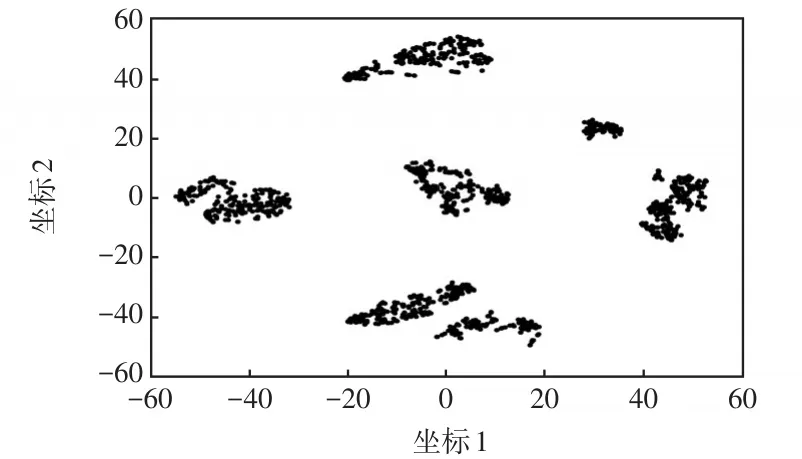
圖4 基于T-sne的可視化圖像Fig.4 Data visualization image based on T-sne

使用K-means和本文方法進行聚類分析，得到5類負荷如圖5和圖6所示。5類負荷包括：①避峰型負荷，負荷使用集中于凌晨和夜晚，而白天使用量較少，一般為酒吧、KTV等夜間場所；②雙峰Ⅰ型負荷，集中在早晚用電且其余時間負荷水平較低，早晨用電也較晚上少，一般為公寓等早晚用電的用戶；③雙峰Ⅱ型負荷，從早上開始持續用電，且飯后用電適當降低，一般為公司、企業等用戶；④重工業負荷，用電一直維持在一個較高的水平；⑤單峰型負荷，一般是輕工業和商業用戶。從圖5可以發現，使用K-means進行聚類時，對類別5單峰型負荷進行了誤判，把兩類形態不同的負荷誤分成了一類，且把同為重工業負荷的類別1和類別2判斷為不同的類別。從圖6可以看出，本文算法能夠對5類數據進行有效識別。

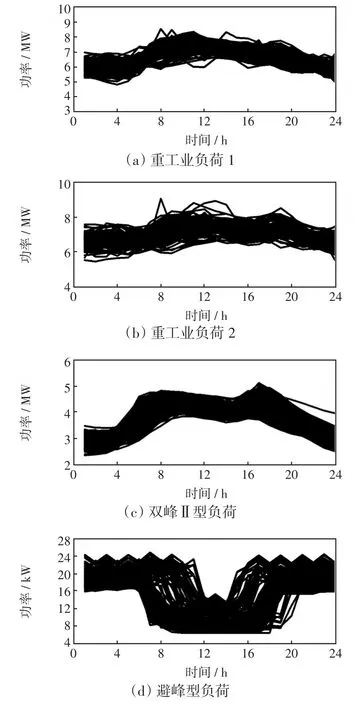
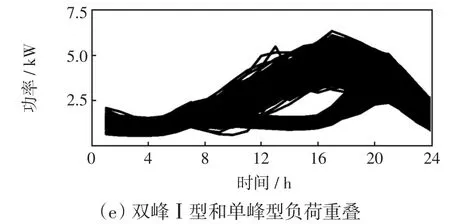
圖5 K-means聚類結果Fig.5 Clustering results obtained using K-means method

圖6 本文方法聚類結果Fig.6 Clustering results obtained using the proposed method

使用T-sne降維對輸出類別進行可視化，如圖7和圖8所示。從圖7可以看出，K-means誤把兩個相距較遠的區域分為了同一類（類別5），且把同一個區域的負荷劃分到了不同的類別（類別1和類別2）。圖8為本文方法類別可視化，可以看出，劃分情況大致滿足類內相似度高，類間相似度低的聚類要求。因此，本文方法效果優于K-means算法。

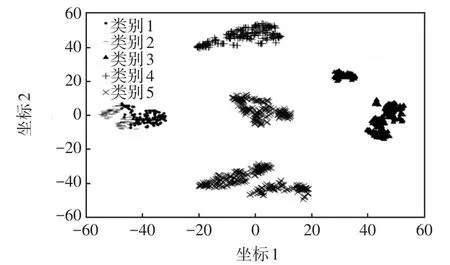
圖7 K-means類別可視化Fig.7 Label visualization obtained using K-means method

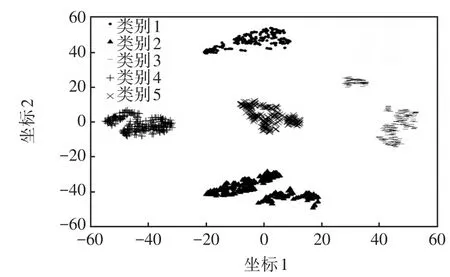
圖8 本文方法類別可視化Fig.8 Label visualization obtained using the proposed method

表1展示了5種方法的SIL與DBI指標，可以看出，在確定最佳聚類數的前提下，中心優化的K-means算法相比于傳統K-means算法DBI要更優；雙尺度K-means算法比傳統K-means算法DBI指標有提升；本文所提方法DBI指標最小且SIL指標最大，聚類質量最佳，說明使用局部密度來優化中心和使用一階差分向量來提取曲線形態的有效性。

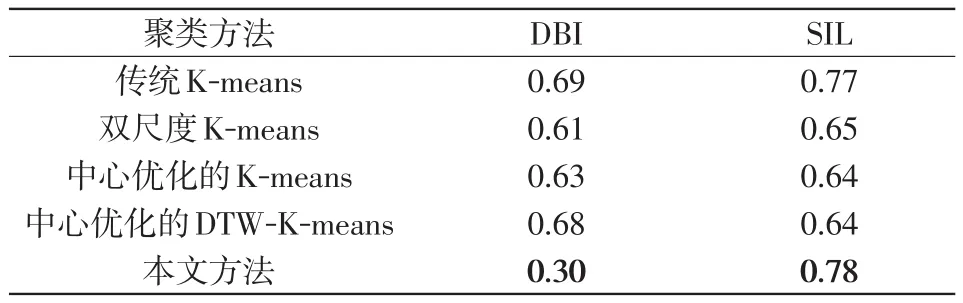
表1 不同算法的聚類指標Tab.1 Clustering indexes of different algorithms

4.3 相似度權重對聚類質量的影響

為了研究相似度權重選取對聚類質量的影響，對不同情況下的權重分配進行比較。對權重進行等間隔分配的實驗。不同權重分配下的聚類指標如表2所示。

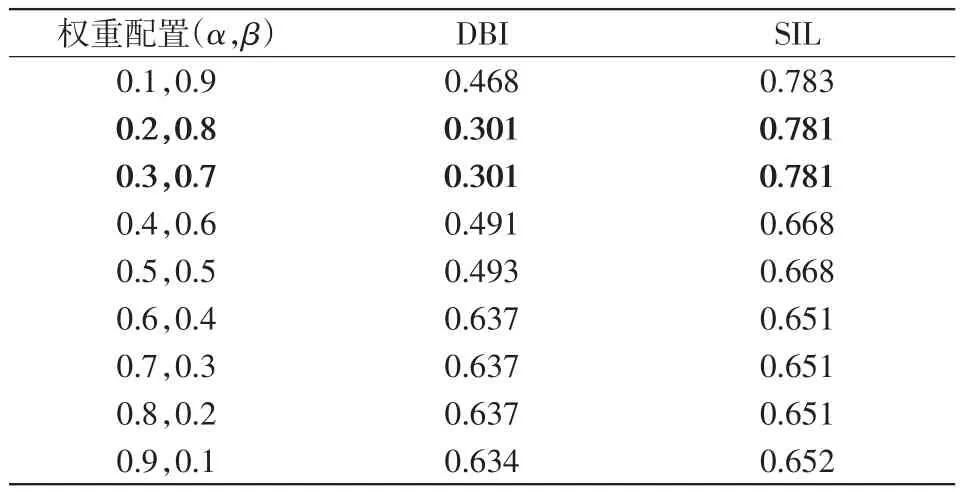
表2 不同權重下的聚類指標Tab.2 Clustering indexes under different weights

從表2可以看出，給予度量不同的權重，聚類的最終效果明顯不同，且權重配置α=0.3及β=0.7，α=0.2及β=0.8時聚類指標最優，本文算例中選用了α=0.3及β=0.7這一權重參數。對于使用多種相似性度量的聚類算法，有必要對每個相似性度量進行度量權重配置，且權重系數的不同配置會導致聚類結果的差異性，所以需要根據實際情況對不同的距離度量分配不同的權重。

5 結語

本文針對電力大數據平臺背景下負荷模式的識別需求，提出一種采用中心優化和雙尺度相似性度量的改進K-means負荷聚類方法。引入局部密度思想獲得負荷曲線的初始中心解決了K-means隨機化帶來的不穩定問題；一階差分向量提取了曲線的趨勢特征，實現了不同曲線形態的準確度量，提升了聚類的準確性。算例分析表明，采用局部密度對中心進行優化，增強了算法的穩健性，改進了傳統K-means算法中初始中心影響聚類效果的問題，且使用一階差分向量提取曲線的趨勢特征，以雙尺度相似性作為依據兼顧了負荷的數值特征和趨勢特征。本文算法相較于傳統算法具有更好的識別負荷趨勢的能力。后續計劃應用本文方法開展負荷預測、氣象災害條件下電力負荷特征提取等方面的研究。