基于TSA-P&O混合算法的光伏多峰值MPPT控制

袁 清 ，趙 斌 ，，王 力 ，倉 啦 ，譚 恒 ，曾祥君

（1.長沙理工大學電氣與信息工程學院，長沙 410114；2.西藏自治區能源研究示范中心，拉薩 850000）

在“碳達峰”、“碳中和”國家戰略性減碳目標的指引下，大力發展可再生能源、逐步降低化石能源比重將是大勢所趨。太陽能作為一種可再生清潔能源已經受到了廣泛關注與使用。然而，目前太陽能發電效率仍然很低，且受天氣、地理位置及組件匹配影響很大，尤其是云層、樹木、建筑物、灰塵等遮擋造成的局部陰影會大大降低光伏發電效率[1]。因此，如何有效解決由于局部陰影等原因造成的光伏陣列失配而引起光伏發電效率低的技術難題，對提高光伏系統發電量至關重要[2]。

在均勻輻照條件下，光伏陣列輸出的P-U特性曲線呈現為單峰形態，此時常規最大功率點跟蹤MPPT（maximum power point tracking）控制算法，例如擾動觀察法P&O（perturb and observe）、增量電導法INC（incremental conductance method）可有效地跟蹤到全局最大功率點GMPP（global maximum power point）。其中，INC算法是P&O的一種派生方法，文獻[3]指出INC算法受噪聲干擾、傳感器檢測精度及控制器的采樣誤差影響很大。文獻[4]提出了一種變步長INC算法，但從仿真結果來看，該方法仍然會在最大功率點MPP（maximum power point）處出現類似P&O的振蕩現象。相比INC算法，P&O實現更為簡單，對傳感器精度要求不高，且可以通過調整步長來降低振蕩。

當光伏陣列中某些組件受到局部遮陰時，受遮陰組件會由于旁路二極管的保護而停止對外輸出電流，從而使得光伏陣列輸出的P-U特性曲線呈現多峰形態，此時P&O和INC算法將難以準確跟蹤到GMPP，從而造成能量損失。智能優化算法由于具有很強的搜索能力，已被廣泛應用于MPPT控制中，例如：細菌覓食算法[5]、雞群算法[6]、差分進化DE（differential evolution）算法[7]、遺傳算法GA（genetic algorithm）[8]、花授粉算法FPA（flower pollination algorithm）[9]、粒子群優化PSO（particle swarm optimization）算法[10]、螢火蟲算法[11]、天牛須算法[12]等。此外，國內外學者提出了多種算法相組合的MPPT控制算法，文獻[13]提出了一種改進模擬退火-粒子群算法，通過調整退火溫度來縮短算法跟蹤時間。文獻[14]提出了一種三步法MPPT控制算法，通過在跟蹤初始階段采用大步長P&O來縮小搜索空間以加快跟蹤速度，然后采用PSO算法進行全局搜索，最后通過P&O進行精細地局部搜索，確保跟蹤精度。文獻[15]提出了一種基于并行組合進化算法的MPPT控制算法，利用GA與DE算法的優勢進行互補。上述多峰值MPPT控制算法均具有全局搜索能力，但上述算法僅從跟蹤精度與速度衡量所提算法的控制性能，卻忽略了控制算法輸出對于跟蹤過程的電壓及功率波動帶來的影響，包括會造成單峰尋優過程中不必要的電壓和功率波動及能量損失。

針對目前現有多峰值MPPT控制算法跟蹤耗時長、跟蹤過程波動性大等問題，提出了一種基于樹種算法TSA（tree seed algorithm）和P&O相結合的光伏多峰值MPPT混合控制算法。該混合控制算法利用光伏P-U特性曲線的單峰/多峰形態識別來加快單峰跟蹤速度，且不影響多峰跟蹤性能；同時采用基于電壓閉環的個體最優化輸出控制策略來抑制電壓和功率波動；最后，通過仿真和實驗驗證了所提控制算法的有效性及可實現性。

1 基于TSA-P&O算法的MPPT控制策略

1.1 樹種算法原理

TSA[16]由土耳其學者Kiran于2015年提出，該算法來源于樹木繁殖方式，相較于其他智能優化算法，其具有結構簡單、搜索精度髙、魯棒性強等特點，已被應用于圖像分割[17-18]等諸多領域。

在TSA中，按照如下公式在搜索空間中生成一批樹木：

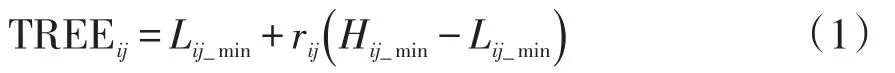
式中：TREEij為第i顆樹上第j維元素；Lij_min、Hij_min分別為第i顆樹上第j維元素的下界和上界；rij為1個隨機數，且rij∈[0,1]。

為了平衡算法的全局搜索能力和局部搜索能力，TSA通過趨勢搜索常數ST來選擇性產生新種子，種子的更新公式分別為

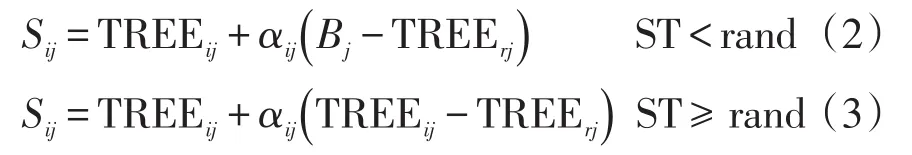
式中：Sij為第i顆樹繁殖的第i顆種子的第j維元素；TREErj為從總體樹中隨機選擇的第r棵樹的第j維元素；Bj為最優樹上的第j維元素；αij為隨機步長因子，且αij∈[-1,1]；ST為趨勢搜索常數；rand為隨機數，且rand∈[0,1]。式（2）主要加強算法的局部搜索能力，式（3）則主要加強算法的全局勘探能力。

1.2 趨勢搜索常數ST取值分析

在TSA算法中，算法進行全局搜索還是局部搜索由趨勢搜索常數ST進行控制，ST取較大值有利于算法的全局搜索，但收斂速度慢；ST取較小值可以使算法加速收斂，但容易陷入局部最優。針對該問題，文獻[17-18]提出了兩種自適應ST取值公式，并在圖像分割上取得了較好效果，但同一種算法在不同應用場合中參數的取值會有所不同，為此，有必要確定在MPPT控制應用上的最佳ST取值。

為了確定ST的最佳取值，仿真實驗模擬了100種隨機陰影下不同ST取值時TSA算法的MPPT控制效果。為評價算法的跟蹤精度及穩定性，采用跟蹤效率及標準差指標，100種隨機陰影分布下算法在不同迭代次數和ST取值的跟蹤效率及標準差如圖1所示，圖1中S1和S2分別為采用文獻[17-18]所提自適應公式的效果，圖1中“迭代10次”的曲線采用左側縱坐標軸，其余均采用右側縱坐標軸。

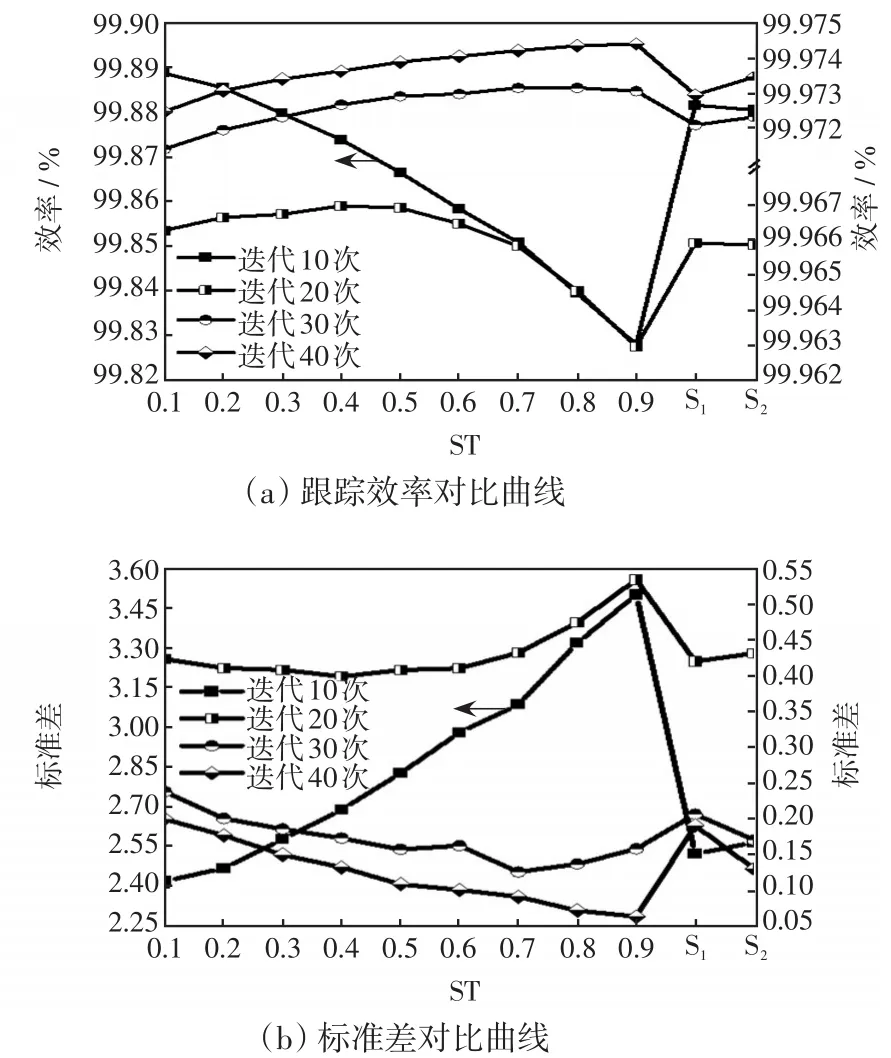
圖1 不同迭代次數與ST取值下TSA算法跟蹤性能Fig.1 Tracking performance of TSA algorithm with different numbers of iterations and ST values

由圖1可知，TSA算法應用于MPPT控制中的精度很高，算法迭代10次即達到99.8%以上的跟蹤效率，且當ST=0.1時取得最大跟蹤效率；當迭代次數為20次時，ST=0.4時取得最大跟蹤效率，而迭代次數大于20次時跟蹤效率和穩定性提升不明顯，且迭代次數的增加意味著MPPT控制算法跟蹤耗時更長。綜合考慮跟蹤效率及穩定性指標，本文取ST=0.4時算法能夠取得最好效果。

1.3 光伏P-U特性曲線的單峰/多峰形態識別

光伏陣列一般安裝在空曠無遮擋位置，工作在均勻輻照條件下，此時光伏輸出的P-U特性曲線呈現為單峰形態，只存在唯一GMPP。在單峰形態下，采用P&O可快速、低振蕩地跟蹤到GMPP，而若單峰形態也通過智能優化算法進行跟蹤，在算法迭代過程中會造成電壓波動和能量損失。為此，本文利用均勻輻照條件下光伏輸出的P-U特性曲線呈現為單峰形態，且在GMPP左側近似為一條直線來進行單峰/多峰形態識別，具體方法如下。

（1）設某光伏陣列由n塊光伏組件串聯組成，MPPT控制算法按如下公式來初始化樹種群位置：

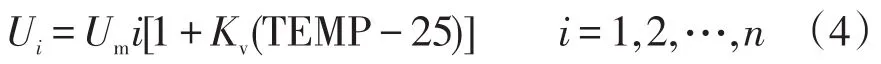
式中：Ui為第i顆樹的初始化電壓位置；Um為光伏組件的MPP電壓；Kv為光伏組件的開路電壓溫度系數；TEMP為組件當前的工作溫度。

（2）通過傳感器采集Ui對應的電流Ii，進而得到功率Pi，通過皮爾遜公式計算出n個采樣點的相關系數，即

（3）通過式（5）計算n個采樣點的相關系數，當r＞ε（ε為判定閾值）時，可判定當前光伏輸出的PU特性曲線近似為單峰形態。通過大量實驗可以得出，ε=0.99時能夠獲得準確的單峰/多峰識別效果。

1.4 基于電壓閉環的個體最優化輸出控制策略

在MPPT控制過程中，由于算法不斷探索尋優而造成的電壓瞬變會使跟蹤過程中出現較大電壓波動，劇烈的電壓振蕩會給電力電子轉換器帶來巨大電壓應力[19]。因此，最大限度地降低算法跟蹤過程中的電壓波動，對于減小開關管電壓應力非常關鍵。然而以往研究往往只關注于算法跟蹤精度與速度，缺乏考慮控制算法的輸出策略對MPPT控制的不利影響，為此，本文提出了一種基于電壓閉環的個體最優化輸出控制策略。

跟蹤過程中引入平均功率波動ΔPavg和平均電壓波動ΔUavg，即

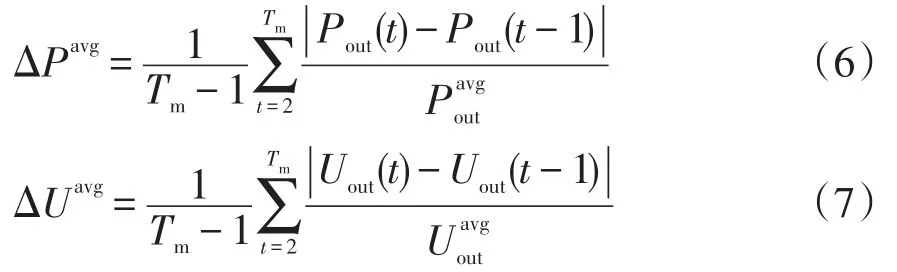
式中：Tm為總采樣周期；t為采樣時刻；Pout(t)為t時刻光伏輸出功率；Uout(t)為t時刻光伏輸出電壓；為光伏陣列在整個運行期間輸出電壓的平均值；為光伏陣列整個運行期間輸出功率平均值。

假設參與算法迭代尋優的個體數目為n，算法在第t-1次迭代中最后一次輸出的個體參考電壓位置記為un(t-1)，由算法計算生成的第t次迭代中新個體參考電壓位置分別記為u1(t),u2(t),…,un(t)，要使得控制算法在第t次迭代跟蹤過程中產生的電壓波動最小，則（fU）必須取最小值。（fU）可表示為

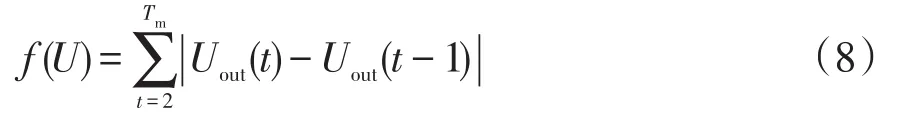
為取（fU）的最小值，可采取以下方法。

（1）將un(t-1)及[u1(t),u2(t),…,un(t)]進行組合形成1個新數組，并對該數組進行升序排序得到y，即y=sort[un(t-1),u1(t),u2(t),…,un(t)]。

（2）找出un(t-1)在輸出數組y中的索引位置k，即k=find[y≡un(t-1)]。

（3）優化后的第t次迭代中個體的參考電壓位置輸出數組U可以表示為

式中：L=miny+(maxy-miny)；yk為第t-1次迭代中最后一次輸出的參考電壓；y1～yk-1和yk-1～yn是經過升序排序后第t次迭代的參考電壓；

通過式（9）所示方法，可以最大程度地抑制控制算法在迭代跟蹤過程中造成的電壓波動，降低開關管在電壓變換瞬間所承受的電壓應力并減小振蕩。

1.5 基于TSA-P&O算法的MPPT控制

基于TSA-P&O算法的MPPT控制采用電壓閉環控制方式[21]調節光伏輸出電壓以實現MPPT，光伏輸出功率優化模型可表示為。

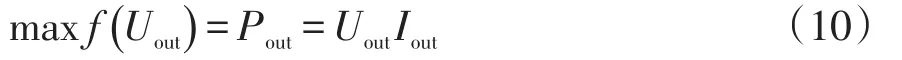
式中，Uout、Iout、Pout分別為光伏陣列工作點的電壓、電流和功率。

基于TSA-P&O算法的光伏MPPT控制系統框圖如圖2所示。圖2中主電路拓撲結構為同步Buck電路。為提高檢測精度，避免誤檢測對控制性能的影響，對傳感器輸入的電壓與電流信號進行模擬濾波并通過模數轉換轉化為數字信號，然后進行數字濾波以降低噪聲干擾，再將濾波后的電壓和電流信號送入MPPT控制器。MPPT控制器使用S函數，其通過獲取光伏陣列的輸出電壓及輸出電流計算得到輸出參考電壓，該參考電壓與光伏陣列當前輸出的實際電壓作差得到的偏差信號送至PID控制器，再由PID控制器輸出占空比信號至脈沖寬度調制PWM（pulse width modulation）發生器，最后通過PWM發生器產生占空比可變的PWM信號至金屬-氧化物半導體場效應晶體管MOSFET（metal-oxidesemiconductor field-effect transistor）門極驅動器對MOSFET進行開斷控制。整個系統采用電壓閉環控制方式將光伏陣列的端電壓調節至GMPP電壓處，以實現MPPT控制。

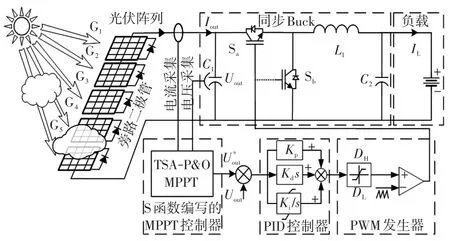
圖2 基于TSA-P&O算法的MPPT控制系統Fig.2 MPPT control system based on TSA-P&O algorith

基于TSA-P&O算法的MPPT控制流程如圖3所示。為了使算法適應輻照度變化，當檢測到前后兩次功率值變化不小于5%時，重啟算法[20]，即

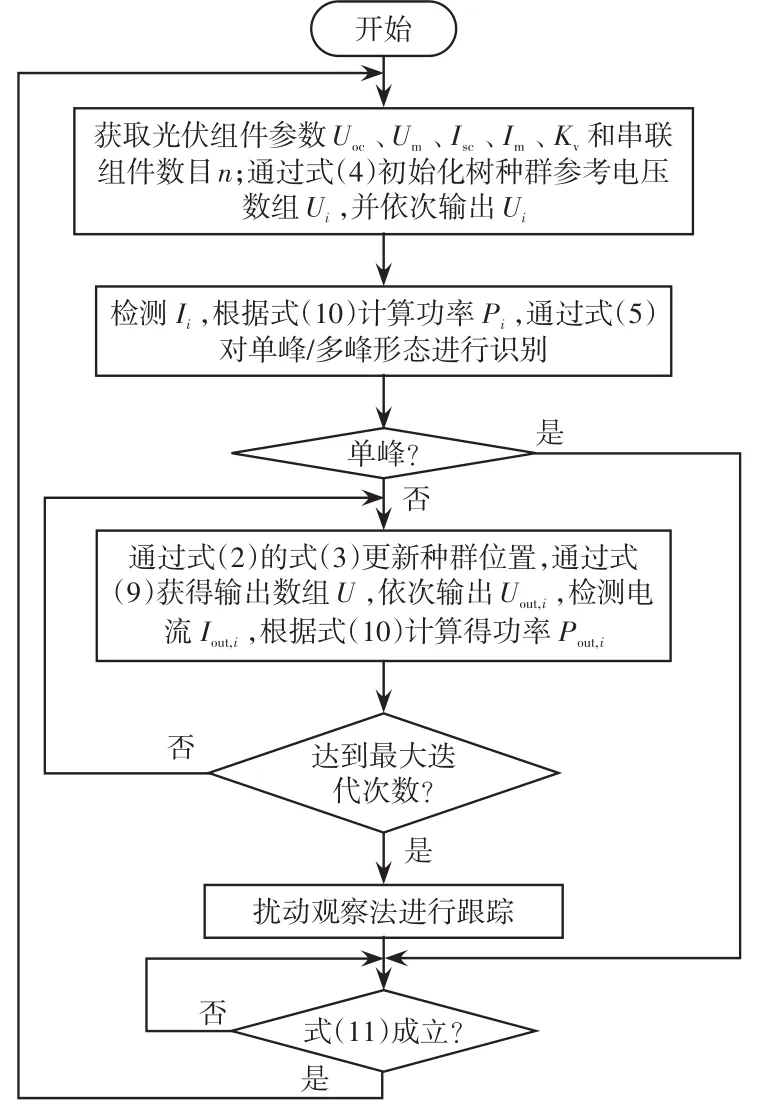
圖3 基于TSA-P&O算法的MPPT控制流程Fig.3 Flow chart of MPPT control based on TSA-P&O algorith

式中，Pt為t時刻光伏輸出功率。

2 仿真與結果分析

為了驗證TSA-P&O混合控制算法的正確性和有效性，使用Matlab/Simulink搭建了如圖2所示的光伏MPPT控制系統，該系統包括光伏陣列、同步Buck變換器及12 V蓄電池負載。其中光伏陣列采用5塊光伏組件串聯連接，每塊光伏組件兩端均并聯有1個旁路二極管，光伏陣列輸出端串聯有1個防倒灌阻塞二極管。光伏組件參數為MMP電壓Um=11.72 V，MMP電流Im=1.85 A，開路電壓Uoc=14.33 V，短路電流Isc=2.01 A，開路電壓溫度系數Kv=-0.36%/℃。同步Buck變換器參數為輸入電容200 μF，輸出電容200 μF，電感15 μH。系統控制參數為開關頻率250 kHz，采樣頻率25 kHz，控制頻率500 Hz。蓄電池參數為標稱電壓12 V，滿充電壓13.97 V，截止電壓10.5 V，額定容量60 A·h，初始荷電狀態為50%。

為了驗證算法在復雜陰影和溫度變化下的跟蹤性能，仿真實驗共設置了5種工況條件，每種工況的輻照度與溫度如表1所示，光伏陣列在5種工況條件下輸出的P-U特性曲線如圖4所示。由圖4可知，隨著溫度的變化，光伏陣列的開路電壓也發生明顯變化，且不同工況下GMPP位置均不相同。

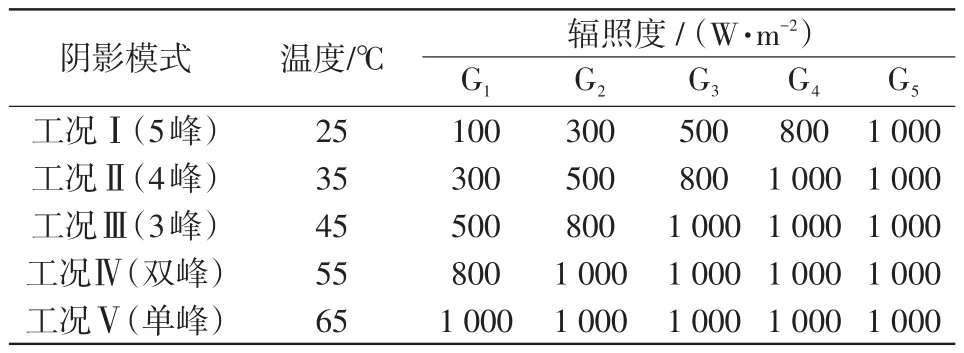
表1 光伏組件所受光輻照度與溫度Tab.1 Irradiance and temperature of PV modules

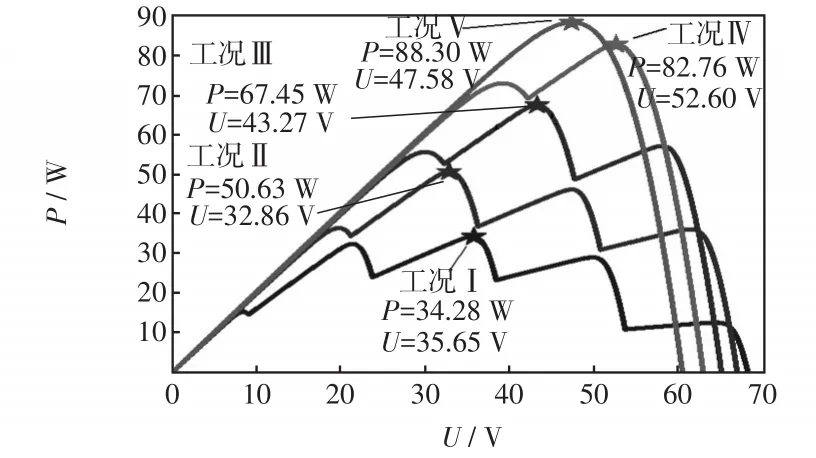
圖4 不同輻照度和溫度下的光伏陣列P-U特性曲線Fig.4 P-U characteristic curves of PV array at different irradiances and temperatures

在仿真中采用陰影變化模式進行算法性能測試，這樣既可以測試算法在靜態工況下的穩態跟蹤精度，又可以驗證算法在工況變化下的動態跟蹤性能。因此，仿真實驗通過工況Ⅰ→工況Ⅱ→工況Ⅲ→工況Ⅳ→工況Ⅴ的變化順序來對TSA-P&O、GA、FPA、PSO、DE共5種算法進行性能對比檢驗，同時設置每種工況切換的時間間隔為0.3 s。其中，設置TSA-P&O算法的趨勢搜索常數ST=0.4；設置GA算法的變異參數ρ=0.1，交叉概率Cr=0.8；設置FPA算法的轉換概率Ra=0.8；設置粒子群算法的加速因子c1=c2=2，慣性權重ω=0.08，最大速度vmax=2；設置DE算法的縮放因子F=0.6，交叉概率Cr=0.67。上述5種MPPT控制方法僅為控制算法不同，其余部分均相同。

不同工況下5種MPPT控制算法跟蹤過程中功率波形如圖5（a）所示，電壓波形如圖5（b）所示。整個仿真過程的運行結果如表2所示。表2中，ttrack為跟蹤時間；靜態跟蹤精度η0表示算法在特定工況下的穩態跟蹤精度；動態跟蹤效率ηd表示光伏系統在一個時間段內總的跟蹤效率，可以反映出算法跟蹤過程中的能量損失。η0和ηd的計算公式分別為

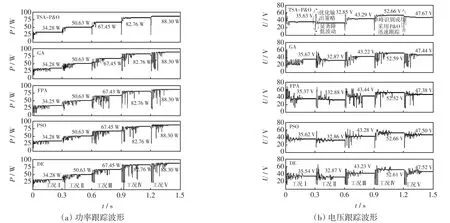
圖5 動態工況下5種控制算法的仿真波形Fig.5 Simulation waveforms of five control algorithms under dynamic working conditions

表2 動態工況下5種控制算法的仿真結果Tab.2 Simulation results of five control algorithms under dynamic working conditions

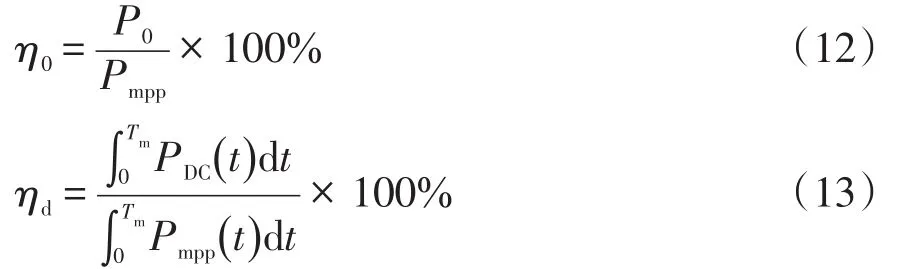
式中：P0為算法跟蹤到的實際功率；Pmpp為光伏提供的理論最大功率；PDC(t)為t時刻Buck電路輸入功率；Pmpp(t)為t時刻光伏提供的理論最大功率。

從圖5和表2的仿真結果可以得出如下結論。

（1）對于跟蹤時間，TSA-P&O算法在5種工況下均具有最短跟蹤時間，特別是對于工況Ⅴ（單峰），因為TSA-P&O算法具有光伏輸出P-U特性曲線的單峰/多峰形態識別策略，當算法成功檢測到當前為單峰形態時，采用P&O進行快速低振蕩跟蹤，僅耗時10ms就成功地跟蹤到GMPP。

（2）對于靜態跟蹤精度，在5種工況下，5種控制算法的跟蹤精度均很高，除FPA算法在工況Ⅰ（5峰）和工況Ⅲ（3峰）下靜態跟蹤精度分別為99.91%和99.97%外，其余算法的跟蹤精度均達到99.99%。由此可以看出，不同算法跟蹤精度相差不大，而在確保跟蹤精度前提下保證跟蹤快速性，以及降低跟蹤過程的電壓和功率波動也較為關鍵。

（3）對于電壓和功率波動，TSA-P&O算法在這兩項指標上均具有最低值，即相比其他4種算法，采用該控制算法在整個跟蹤過程中具有最低的電壓和功率波動，說明引入基于電壓閉環的個體最優化輸出控制策略，可以極大地抑制跟蹤過程中的電壓和功率波動。

（4）對于運行期間所獲得能量和動態跟蹤效率，TSA-P&O算法獲得的能量E最高，E=95.47 J，其動態跟蹤效率也最高，ηd=98.39%。其他4種算法所獲能量由高到低依次為PSO、GA、DE、FPA，所獲能量E分別為92.11 J、91.15 J、90.74 J、90.13 J，對應動態跟蹤效率ηd分別為94.93%、93.94%、93.51%、92.89%。

通過以上對比分析可知，在5種工況下的MPPT跟蹤全過程中，TSA-P&O算法各項指標的綜合性能優于其他4種算法，且針對單峰形態的跟蹤效果非常好，驗證了所提出的光伏P-U特性曲線單峰/多峰形態識別策略的正確性。通過對不同算法多種工況下的電壓及功率波形進行對比，驗證了基于電壓閉環的個體最優化輸出控制策略的有效性。

3 實驗與結果分析

3.1 實驗系統構建

為了進一步驗證基于TSA-P&O混合控制算法的有效性和可實現性，設計并制作了1個最大功率為200 W、最大輸入電壓為80 V的MPPT硬件原型系統，并進行實驗。圖6為基于STM32的光伏MPPT控制系統實驗平臺，其中實驗所用設備主要包括光伏模擬源（ITECH-IT6512C，80 V/120 A/1 800 W）、數字式虛擬示波器（OSCA02E，60 MHz）、同步Buck電路控制板（80 V/200 W）、12 V蓄電池負載（VARTA，12 V/60 AH）及計算機等。

圖6 MPPT控制系統實驗平臺Fig.6 Experimental platform of MPPT control system

光伏模擬源通過上位機軟件控制來模擬光伏陣列輸出，限于光伏模擬源的動態響應速度，為了使在下一個MPPT控制周期光伏模擬源的輸出已經進入穩態，實驗設置MPPT控制周期為300ms[22]。

Buck電路元器件參數和仿真配置一致，整個光伏控制系統核心部分采用STM32G474單片機作為主控制器，其在系統中主要實現對光伏模擬源輸出的電壓和電流信號進行采集、數字濾波及控制算法計算，并根據算法計算結果實時輸出PWM信號對同步Buck電路進行電壓閉環控制，以實現GMPP跟蹤。同時，為了使實驗和仿真相對應，實驗部分選擇的光伏組件參數及陰影變化模式與仿真配置一致，實驗中陰影模式的切換間隔設置為35 s。由于光伏模擬源上位機軟件無法對溫度進行設定且取值固定為25℃，因此實驗部分所有工況下溫度均為25℃。

3.2 結果對比分析

通過光伏模擬源上位機軟件記錄的5種算法跟蹤結果如表3所示。示波器記錄的基于TSAP&O、GA、FPA、PSO、DE等5種算法在動態工況下MPPT控制過程中的電壓、電流及功率波形如圖7所示。下面對跟蹤速度、精度及跟蹤過程中電壓和功率波動3個指標進行對比分析。

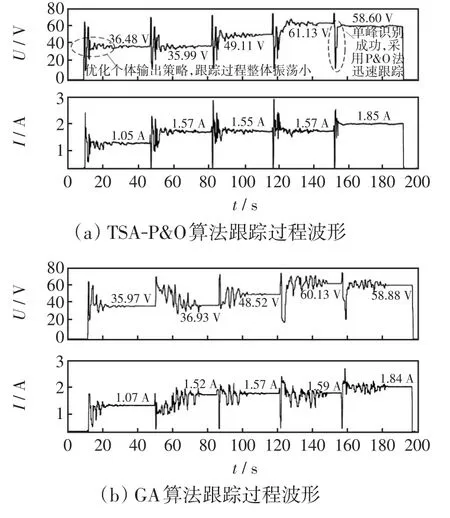
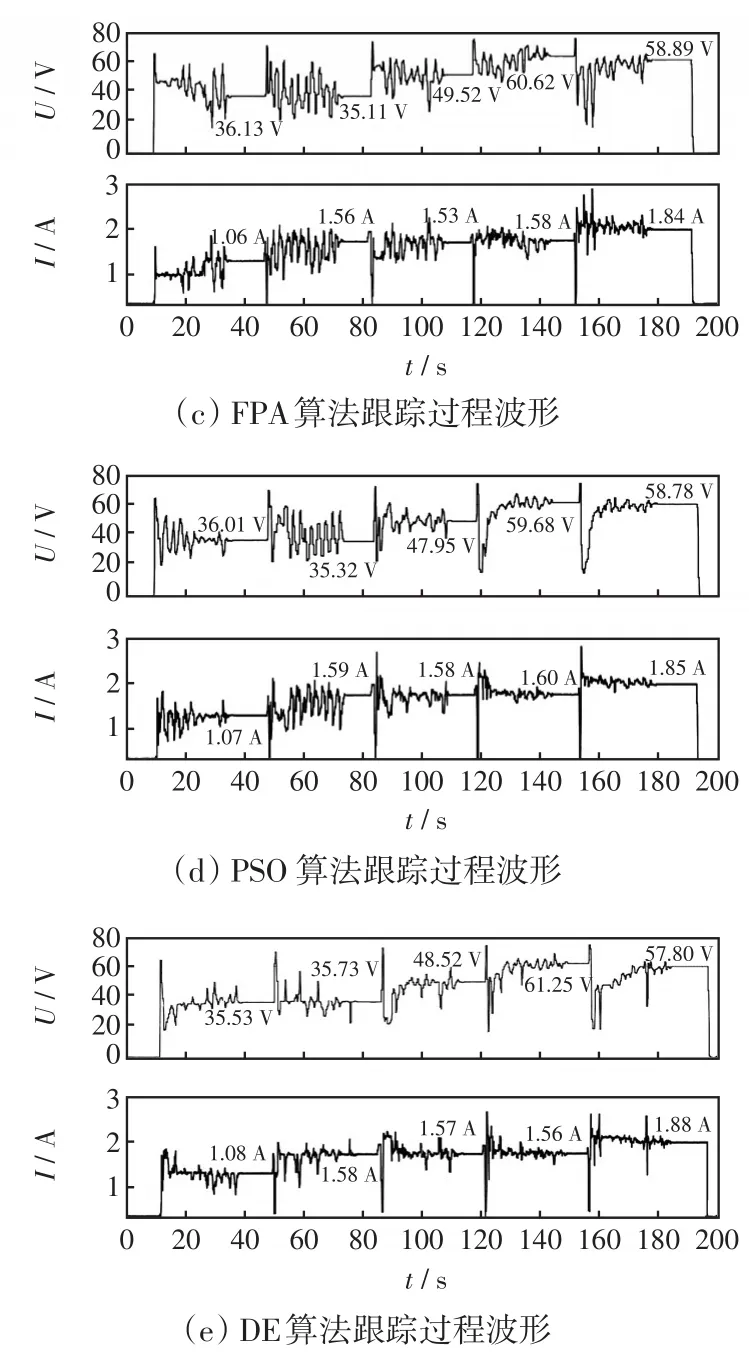
圖7 動態工況下5種控制算法的實驗波形Fig.7 Experimental waveforms of five control algorithms under dynamic working conditions

表3 動態工況下5種控制算法的實驗結果Tab.3 Experimental results of five control algorithms under dynamic working conditions

從表3和圖7的仿真結果可以得出如下結論。

（1）對于跟蹤時間，TSA-P&O算法在5種陰影模式下均具有最低值，特別是在工況Ⅴ（單峰）下的跟蹤速度非常快，這是由于控制算法具有單峰/多峰形態識別策略，當檢測到單峰形態時，迅速切換到P&O算法進行跟蹤，僅用3.5 s就跟蹤到了GMPP，進一步驗證了所提單峰/多峰形態識別策略的正確性和有效性。

（2）對于靜態跟蹤效率，僅TSA-P&O和DE兩種算法在5種工況下均達到了99.9%；對于動態跟蹤效率，5種算法由高到低依次為TSA-P&O、DE、GA、PSO、FPA，對應的動態跟蹤效率分別為96%、94%、94%、93%、92%，驗證了TSA-P&O算法具有很高的跟蹤精度和較低的能量損失。

（3）對于電壓和功率波動，從圖7可以看出，由于TSA-P&O算法具有基于電壓閉環的個體最優化輸出控制策略，使得整個跟蹤過程中電壓和功率波動很小；而其他4種算法的電壓和功率波動非常明顯，這不僅會加大功率管在電壓變換瞬間所承受的電壓應力，且會造成能量損失。

4 結論

本文針對局部陰影等原因造成光伏功率輸出多峰值問題提出了一種新型混合控制算法，并使用Simulink仿真和實驗驗證了算法的正確性，通過對仿真和實驗的結果分析，得出主要結論如下：

（1）提出的混合控制算法可將TSA的全局搜索能力與擾動觀察法的局部搜索能力有效結合，提高了算法的跟蹤精度與跟蹤速度；

（2）通過在控制算法中加入光伏P-U特性曲線單峰/多峰形態識別策略，可有效提高算法在單峰條件下的跟蹤速度，同時具有光伏多峰跟蹤性能；

（3）通過建立的電壓和功率波動的評價指標，驗證了提出的采用基于電壓閉環的個體最優化輸出控制策略，可以最大程度地抑制算法迭代跟蹤過程中的電壓和功率波動，減小跟蹤過程中的能量損失。