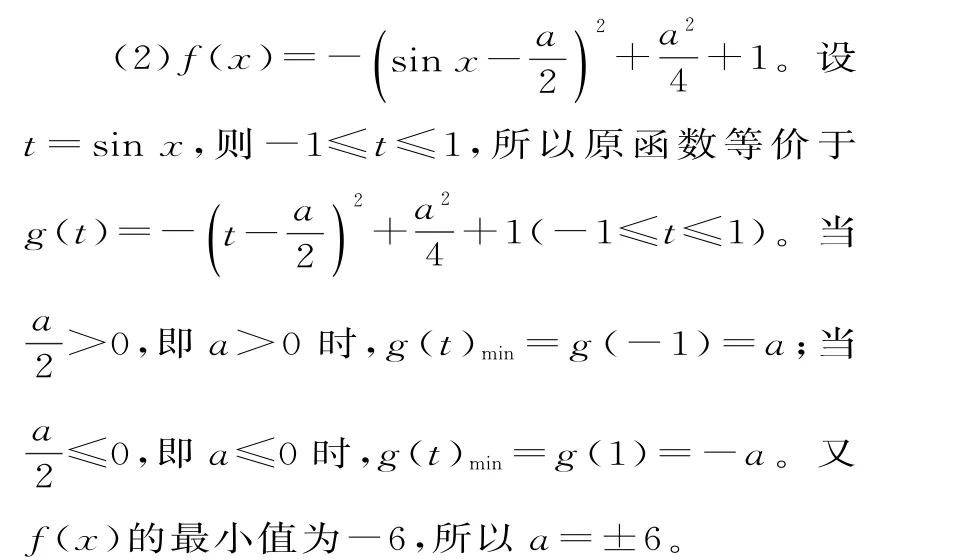三角函數與二次函數的綜合問題
2022-01-17 09:31:30黃林平
中學生數理化·高一版 2021年12期
■黃林平
第四章我們學習了指數函數、對數函數與二次函數的綜合問題,運用類比學習的方法,來研究三角函數與二次函數的綜合問題。下面從二次函數的“身份”明顯、二次函數的“身份”不明顯兩個方面舉例說明。
一、二次函數的“身份”明顯
二次函數的“身份”明顯,即在二次函數的系數或常數項中含有三角函數,此類問題不難解決,但要注意三角函數的有界性。可謂是二次函數“搭橋”,三角函數“唱戲”。
二、二次函數的“身份”不明顯
形如y=asin2θ+bsinθ+c(a≠0)或y=acos2θ+bcosθ+c(a≠0)的函數,表面上看是三角函數,二次函數的“身份”不明顯,可利用換元法轉化為二次函數。這類問題的本質沒有變,仍然是已學過的二次函數,可謂是“新瓶裝舊酒”。

(1)當a=2時,求函數f(x)的值域。
(2)若f(x)的最小值為-6,求a的值。
提示:(1)當a=2時,f(x)=-(sinx-1)2+2。設t=sinx,則-1≤t≤1,所以原函數等價于函數g(t)=-(t-1)2+2。由-1≤t≤1,可得-2≤g(t)≤2,即f(x)的值域為[-2,2]。