同型光熱發電機并聯聚合對光熱發電場振蕩穩定性影響

賴林琛 周 強 杜文娟 王 楊 王海風

同型光熱發電機并聯聚合對光熱發電場振蕩穩定性影響

賴林琛1周 強2杜文娟1王 楊1王海風1

（1．四川大學電氣工程學院 成都 610065 2．國網甘肅省電力公司電力科學研究院 蘭州 730050）

該文研究了并聯光熱發電機群聚合對光熱發電場振蕩穩定性的影響，發現并聯光熱發電機數量增加時，與光熱發電機勵磁系統相關的振蕩模式在復平面上向右移動，給光熱發電場帶來失穩風險。文中采用勞斯穩定判據，進一步分析證實并解釋了這一發現的機理。該文首先給出了光熱發電機組線性化模型，進而建立了含臺并聯光熱發電機的光熱發電場線性化模型；然后，在光熱發電機模型相同的條件下，采用相似變換推導了光熱發電場等效模型，分析了并聯光熱發電機數量增加給光熱發電場帶來振蕩失穩的風險，通過算例演示了隨著并聯光熱發電機數量的增加，光熱發電場的勵磁振蕩模式在復平面上向右移動，導致光熱發電場振蕩失穩，探討了光熱發電機運行狀態不同時等效模型的適用性；最后通過理論分析表明，光熱發電機機電振蕩模式不受并聯光熱發電機數量增加的影響，從而證明和解釋了勵磁振蕩模式失穩的機理。

光熱發電機 動態聚合 振蕩穩定性 光熱發電場

0 引言

作為太陽能發電中的新興產業，光熱發電正在全球范圍內得到快速發展與廣泛應用[1-3]。據世界能源署預計，2020年美國和歐洲光熱發電量可占發電總量的3%，2025年全世界光熱裝機容量將達到22GW，2050年全世界光熱發電量可占全球總發電量的11.3%[4]。大規模光熱發電機（Concentrating Solar Power, CSP）并網將給電力系統運行穩定性問題帶來挑戰。考慮到光熱機組容量較小，大規模光熱接入系統模型階數會隨并入機組數量的增加而增高[5]。為降低檢測振蕩增長風險的復雜性和計算負擔，通常需要使用聚合動態模型。

光熱機組與傳統的火電機組均使用傳統的汽輪機進行發電，故它們的動態特性相似。同步發電機的聚合方法早已有了較多的研究，其中有基于發電機轉子同擺的最基本的同調等值法[6]。在同調等值法的相關機群參數聚合中常用的是頻域聚合法[7]，后來基于加權法的發電機及其調節系統詳細模型參數聚合的實用方法被提出[8]。雖然光熱發電技術在向著提升單機容量的方向努力發展[9]，但就目前情況而言，光熱機群單機容量較小，相較于傳統同步機數量較少的聚合臺數[10]，光熱發電機聚合臺數更多。且光熱發電通常采用集中接入的方式，即首先通過集電網絡將光熱發電機組輸出功率匯集至匯流母線，再通過外送系統集中送出，光熱發電系統這一結構特點與傳統多機電力系統不同。

新能源發電技術中，與光熱發電機類似的單機容量較小、采用集中接入方式的風力發電機和光伏發電機的聚合方法有了較多的研究[11-14]。主要有容量加權平均法和參數辨識法，可以用單個發電機導出發電場的聚合動態表示。容量加權平均法是根據發電場中單個發電機的加權參數計算聚合后的參數[15-17]。參數識別方法[18]是最小化發電場與聚合后的發電機在發電場公共耦合點上的動態差異。還有研究提出將多機系統解耦為若干個單機子系統的方法，文獻[19-20]從頻域角度推導了可用于簡化風電場和光伏電場穩定性分析的等效方法；文獻[21]從時域角度提出考慮風電場規模的等效方法，并發現了隨著風電場規模的擴大，系統存在著振蕩失穩的風險。這兩種方法本質相同且對于簡化大規模發電場穩定性問題的分析十分有效。而光熱發電機與風機不同，其并網不通過換流器，多個工程實例均采用發電機—變壓器—線路組單元接線方式并網[9]，光熱發電場是否存在與風電場類似的穩定性問題仍待研究。

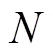
1 同型光熱發電機并聯系統聚合模型

1.1 光熱發電機動態模型

文獻[26]給出了面向控制的光熱發電機數學模型，分別對光熱發電機各子系統進行了不同時間尺度下的研究。為研究光熱發電機并網系統的振蕩穩定性，在文獻[26]的基礎上進行一些合理的修改，本文將光熱發電機的聚光集熱子系統、蓄熱子系統、發電子系統聯系起來，得到了可用于電力系統振蕩穩定性研究的光熱發電機模型。太陽能光熱發電的主要原理如圖1所示，通過反射太陽光到太陽能接收器進行太陽能的采集，利用傳熱工質（Heat Transfer Fluid, HTF）傳遞、儲存熱量，再通過換熱裝置使鍋爐提供高壓過熱蒸汽驅動傳統的汽輪機進行發電。

圖1 光熱發電原理

1.1.1 聚光集熱、蓄熱子系統模型

光熱發電機的聚光集熱子系統和蓄熱子系統模型如圖2所示。

圖2 集熱與蓄熱子系統模型

集熱子系統中，傳熱工質從接收器入口開始向出口流動，并在接收器中吸收來自太陽的熱量，最終經管道流入蓄熱子系統。蓄熱子系統中，HTF從熱罐流出，經過換熱器將熱量傳至鍋爐，換熱后的HTF流入冷罐并被繼續送至集熱子系統。

1）聚光集熱子系統模型

接收器中，熱量的傳遞主要發生在導管（tube）和HTF之間。

接收器入口處的熱力學過程為：導管接收反射鏡聚集的太陽光的熱量，并傳遞至管中的HTF；對于HTF，其吸收的熱量來自導管，在其流動的過程中也會散失部分熱量；故太陽能接收器入口處熱力學動態方程為

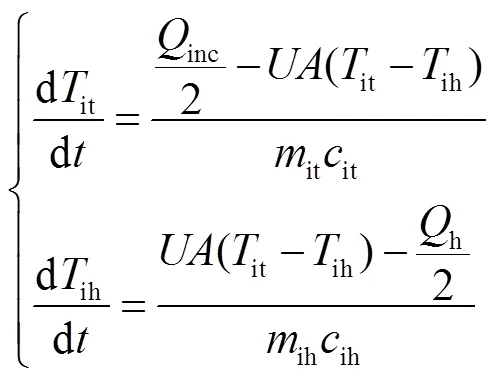
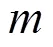
接收器出口處的熱力學過程與接收器入口處相同，故其熱力學動態方程為

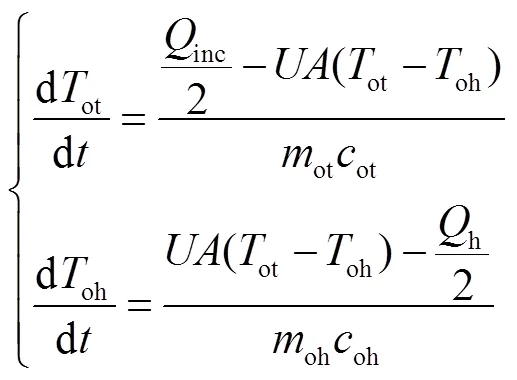
式中，下標ot表示接收器出口處導管的物理量；下標oh表示接收器出口處HTF的物理量。

式（1）、式（2）構成了光熱發電機聚光集熱子系統的熱力學模型。

2）蓄熱子系統模型

由圖2中蓄熱子系統部分熱量流動框圖可知，熱罐、冷罐的溫度的變化主要由流入HTF帶來熱量和流出HTF帶走熱量的差值決定，且流入的HTF和流出的HTF的質量可認為是恒等的，故可得描述蓄熱子系統熱力學過程的動態方程為

3）聚光集熱及蓄熱子系統模型

由圖2可知，太陽能接收器中，HTF的流入流出導致的熱量變化為流入接收器入口處與流出接收器出口處HTF熱量的差值；HTF從接收器中流出，經過管道流入熱罐過程中存在熱量損耗；換熱器向鍋爐注入的熱量為流入和流出換流器HTF熱量的差值，故可得

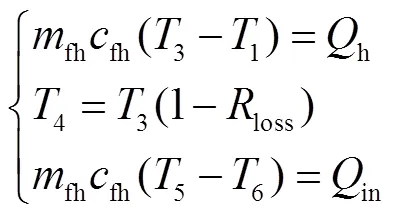
為了計算方便，在實際處理時近似地認為太陽能接收器入口處HTF的溫度與流入其中的HTF的溫度相等，太陽能接收器出口處HTF的溫度與從其流出的HTF的溫度相等，熱罐中HTF的溫度與從其流出的HTF的溫度相等，即

式（1）～式（5）共同構成了太陽能光熱發電機的熱力學部分模型，即聚光集熱子系統及蓄熱子系統的模型。

1.1.2 發電子系統模型

光熱發電機的發電子系統模型采用文獻[26]中給出的可用于研究振蕩穩定性的發電子系統模型及參數，包含發電機的磁鏈5階、軸系六質塊12階及勵磁系統3階方程，該模型與傳統同步機模型基本相同，故發電子系統非線性動態模型不做贅述，僅給出線性化模型，即

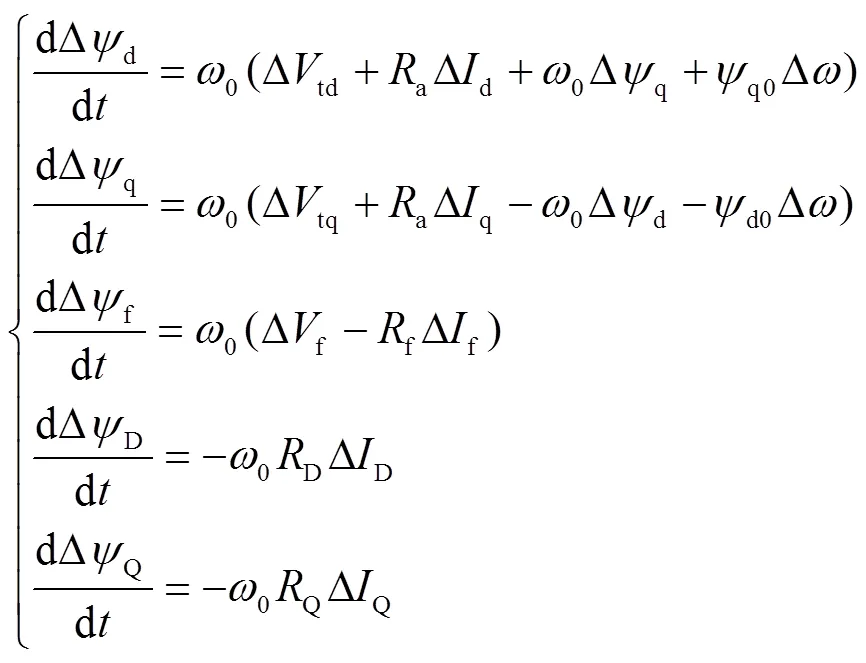
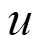
圖3 調速器控制模型

從圖3可以得到調速器的線性化動態方程為

1.1.3 鍋爐部分模型

1.1.4 光熱發電機線性化模型

由此前的建模過程可知，光熱發電機的集熱蓄熱子系統和發電子系統可以直接簡單地通過鍋爐能量轉換模型聯系起來，將二者互聯可得整個光熱發電機的數學模型。

將式（10）線性化可得

將式（1）～式（5）線性化可得

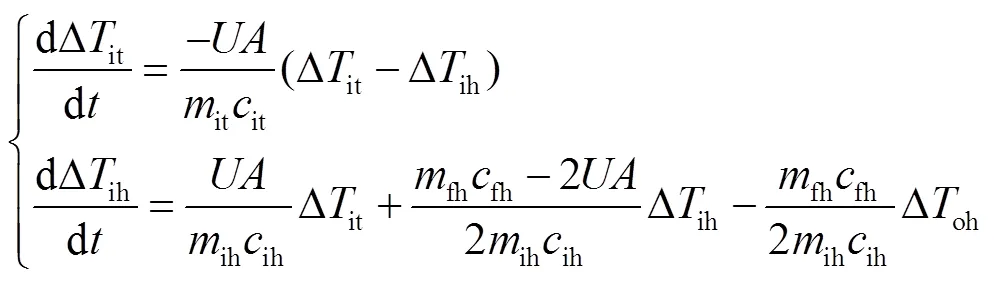
將式（11）～式（14）與式（6）～式（9）結合，可得到光熱發電機線性化模型為

1.2 并聯光熱發電機等效模型

光熱發電機并聯聚合方法參考文獻[21]中提出的聚合方法。

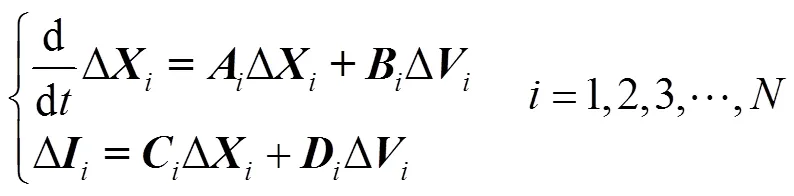
由圖4可得到并聯光熱發電機群的狀態空間模型為

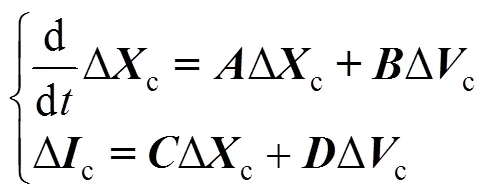
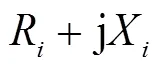
其中

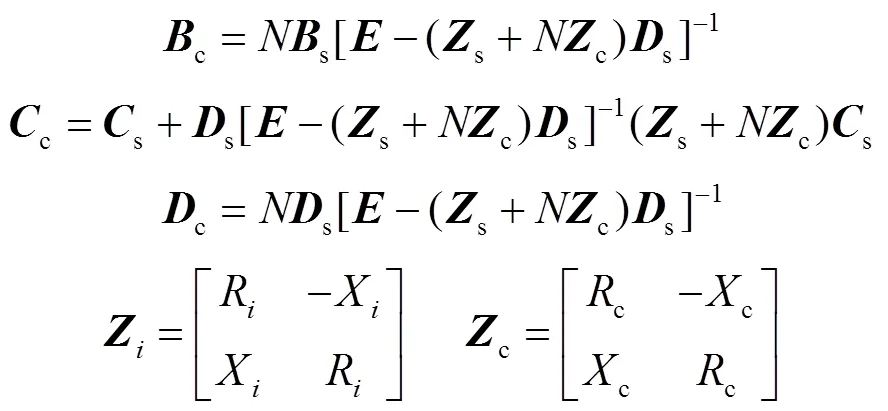
式中，為等效后得到的新的狀態變量組成的向量為2×2的單位矩陣。

式（18）稱為并聯光熱發電機群的等效模型。觀察式（18）可以發現，圖4中所示的系統可以由圖5和圖6表示的個獨立的等效子系統。

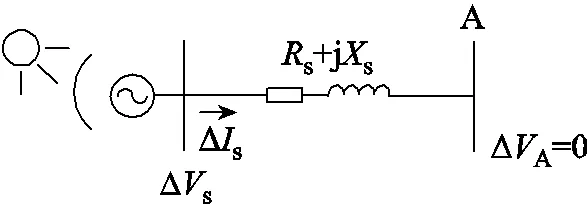
圖5 前N-1個等效子系統

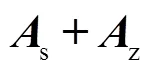
圖6 第個等效子系統

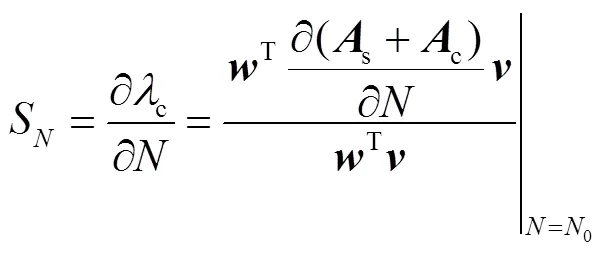
由圖6所示的第個等效子系統模型，還可得用于非線性仿真分析的光熱發電機群聚合模型，具體如圖7所示。本節此前的推導中不涉及外部電力系統，圖7中外部電力系統模型和參數同圖4。對于光熱發電場，其線性化模型仍如式（18）所示，因此，圖7中光熱發電機模型和參數同圖4。但是，光熱發電機與外部電力系統之間的接口處（即圖7中的母線C處）的電壓和電流，應做相應的修改，詳細情況見附錄。

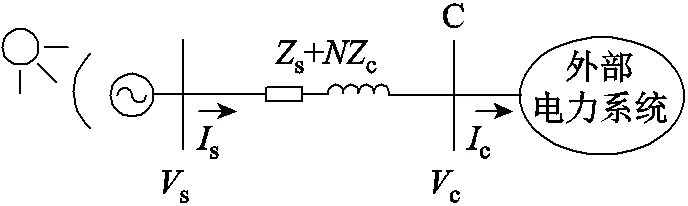
圖7 光熱發電場聚合模型

2 計算分析及仿真

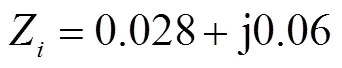
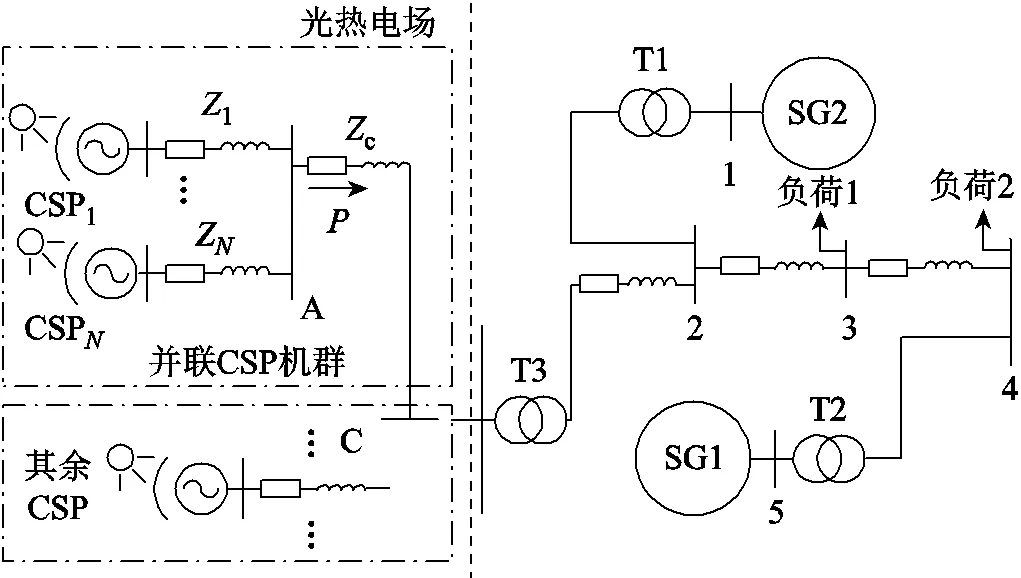
圖8 具有光熱發電場的電力系統

2.1 等效模型

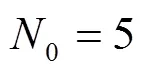
首先，利用式（18）所示等效模型計算并聯光熱發電機群的振蕩模式。計算結果列于表1的前兩列。

表1 5臺光熱發電機并聯并網模型振蕩模式計算結果

Tab.1 Computational results of oscillation modes of group of five CSP generators in parallel connection in the power system

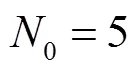
然后，采用式（17）所示全階模型計算并聯光熱發電機的振蕩模式。計算結果見表1中的第三列，其中后綴（×4）表示有四個相同的振蕩模式。

對比表1中三列的結果可知，等效模型可有效反映原光熱發電場的振蕩模式，驗證了1.2節給出的等效模型的有效性。

圖9 特征值對應的參與因子

2.2 并聯光熱發電機數量影響

本節研究并聯光熱發電機數量增加對示例電力系統中的影響。當并聯光熱發電機數量增加時，斷開圖8中相同數量的并網光熱發電場其余部分的光熱發電機。因此，當并聯光熱發電機的數量增加時，光熱發電場整體穩態輸出潮流保持不變。

表2 特征值的運動趨勢指標

Tab.2 Index of movement trend of eigenvalues

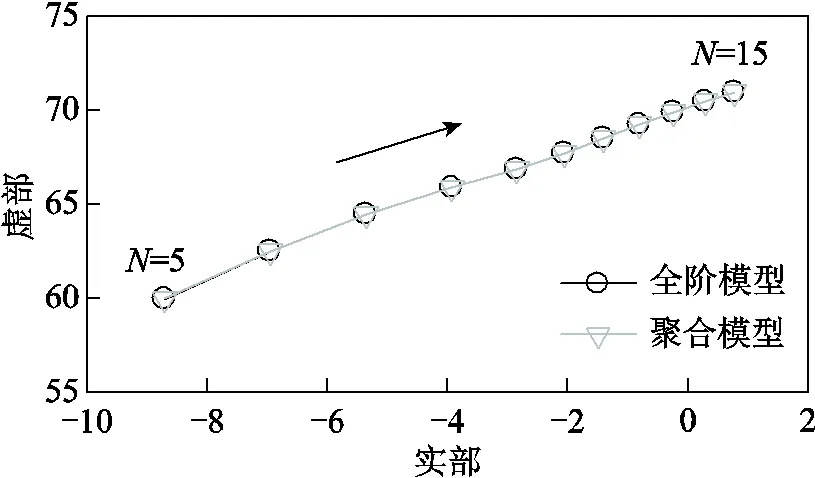
圖10 并聯光熱發電機數量增加時的根軌跡

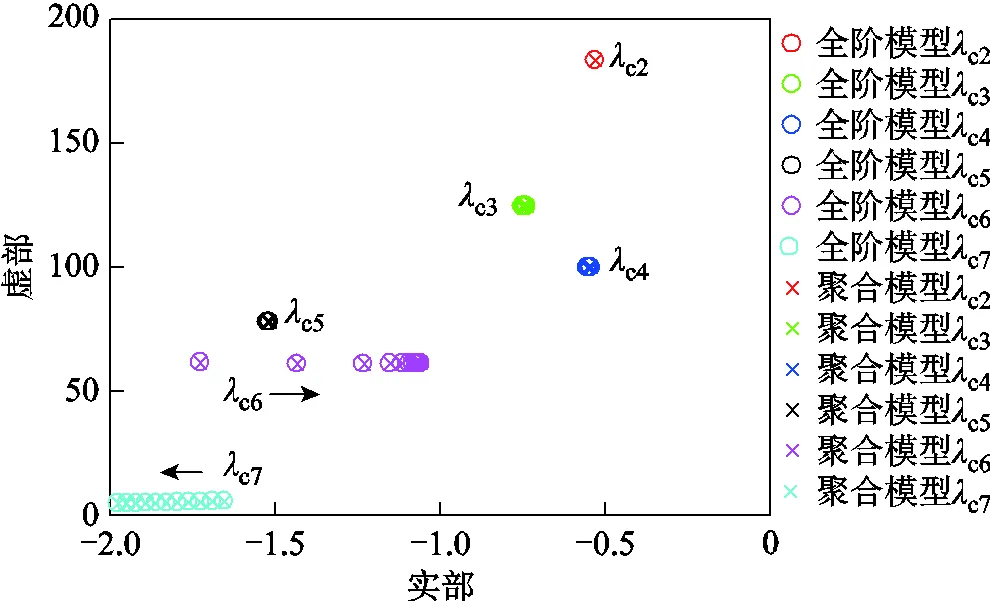
圖11 并聯光熱發電機數量增加時～的根軌跡

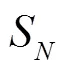
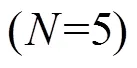
圖12 時非線性仿真結果

2.3 發電機動態存在差異

2.1節和2.2節是針對發電機動態相同時的研究，說明了聚合模型的有效性。本小節將發電機的參數設置為不同，以此對聚合模型的適用性進行評估。為針對隨著并聯發電機數量增加而可能失穩的與勵磁系統相關的振蕩模式，將各發電機勵磁系統的參數設置為不同，并且各發電機的出力設置為不同。

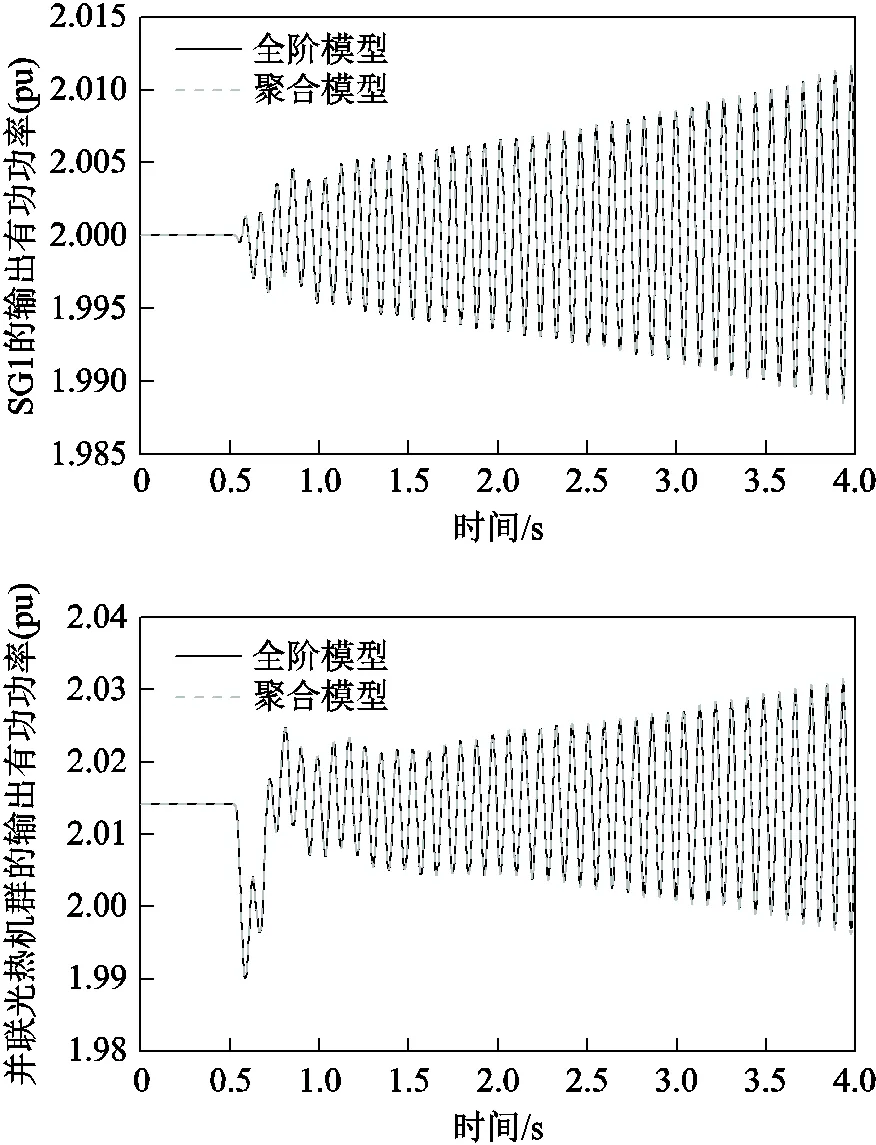
圖13 時非線性仿真結果

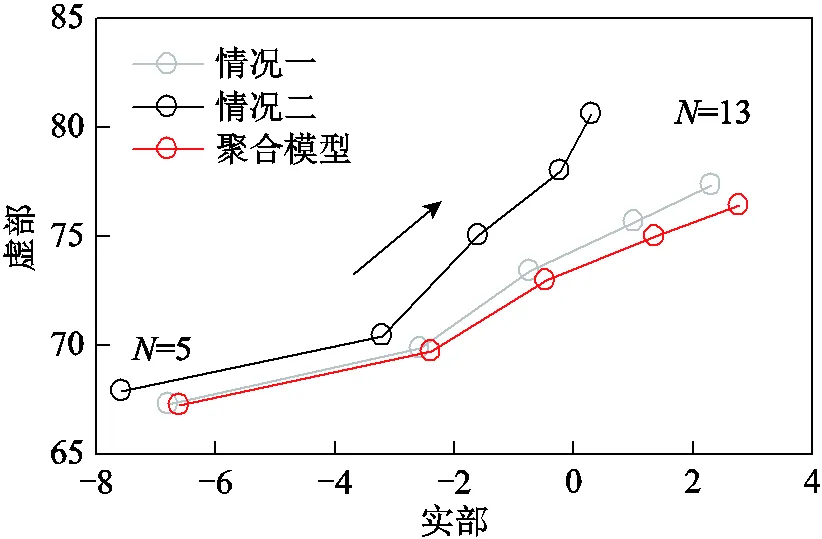
圖14 不同參數情況下的根軌跡

由圖14可知，當=13時，情況一、情況二及聚合模型得到的特征值均位于復平面右半部分，這將導致系統振蕩失穩。說明當發電機動態有一定差異時，聚合模型仍能在一定程度上反映系統可能存在的失穩風險。

最后通過非線性仿真驗證上述結論。仿真中擾動設置為：0.5s時，光熱發電場其余部分的光熱發電機出力增加10%，并于50ms內恢復。仿真結果如圖15所示。

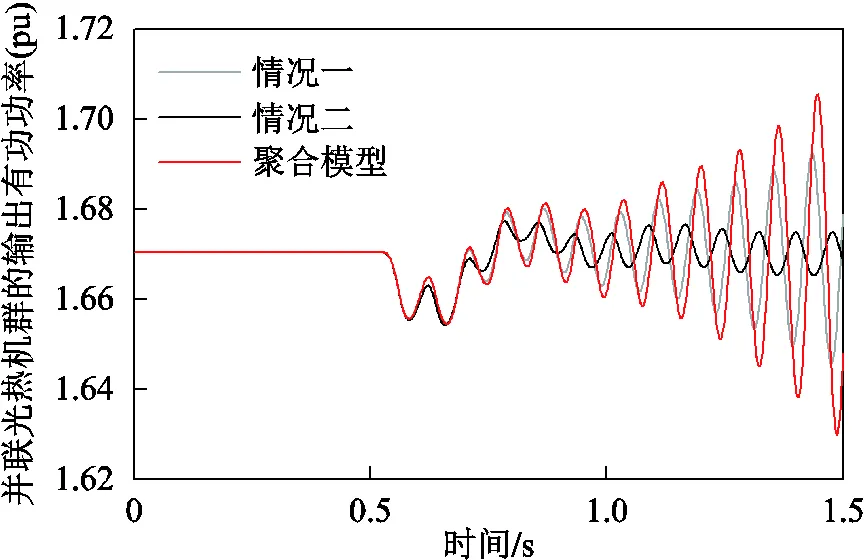
圖15 不同參數情況下的非線性仿真結果

可以看出，=13時情況一、情況二、聚合模型對應的曲線均隨時間發散，系統振蕩失穩，再次驗證了聚合模型在發電機動態存在一定差異時對系統振蕩失穩風險的判定具有一定適用性。

3 系統穩定性分析

2.2節的研究發現，隨著并聯光熱發電機數量增加，僅與勵磁系統相關的振蕩模式可能移動到復平面右半部分，而與軸系相關的振蕩模式均位于復平面左半部分，不會導致系統振蕩失穩。下面將對此給出理論解釋。

從圖6中的聚合模型可知，臺光熱發電機并聯構成機群可以由一臺光熱發電機等效。現考慮一臺光熱發電機接入無窮大母線的情況，具體如圖16所示。

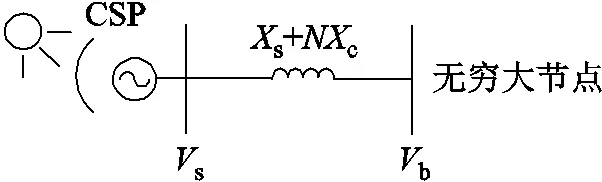
圖16 單臺光熱發電機接入無窮大節點

忽略線路電阻，采用發電機經典模型，即僅含發電機的轉子運動方程，可得系統狀態空間表示形式為

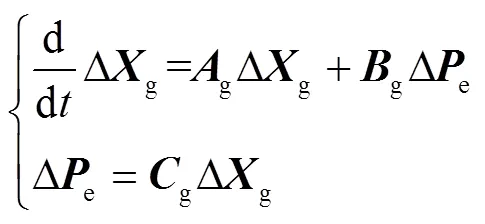
其中

式（20）也可寫為

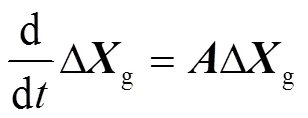
其中

式（21）所示系統特征方程為

由式（22）構建的系統勞斯表見表3。表3中第一列元素均為正。根據勞斯穩定判據，當表3中，第一列所有元素值均大于零時，系統穩定。因此并聯光熱發電機數量增加不會導致系統失穩。

表3 勞斯表

Tab.3 Routh table

結合2.2節的算例分析結果，在光熱發電機中存在兩種振蕩模式：一種是與發電機軸系相關的機電振蕩模式；另一種是與勵磁系統相關的振蕩模式。式（22）表明并聯光熱發電機數量的變化不會導致機電振蕩模式進入復平面右半部分，故可能失穩的只有與勵磁系統相關的振蕩模式，這一結論與算例分析結果完全一致。

4 結論

本文研究了并聯同型光熱發電機接入對光熱發電場振蕩穩定性的影響。所建立模型的計算結果與仿真分析表明了全階模型和等效模型的一致性。

基于等效子系統模型的表示形式和算例分析，重點探討了并聯光熱發電機數量變化對光熱發電機群振蕩穩定性的影響，得出以下結論：

1）光熱發電機群內并聯機組數量變化會導致聚合模型振蕩模式中與勵磁系統相關的振蕩模式在復平面上向右移動；當并聯光熱發電數量達到一定值時，該振蕩模式可能進入復平面右半部分，導致系統振蕩失穩。

2）從算例中可知，當光熱發電機群內發電機動態存在一定差異時，聚合模型仍能在一定程度上反映出系統可能存在的振蕩失穩風險。

3）并聯光熱發電機群內，與光熱發電機軸系相關的機電振蕩模式基本不受并聯光熱發電機數量變化的影響。理論推導也證明和解釋了這一結論。

本文針對并聯型光熱發電機群進行了模型推導和計算仿真分析，分析結果對于目前工程實際中的大型光熱發電場的規劃運行具有指導性意義。但是，隨著光熱發電技術的發展，光熱發電場的拓撲結構可能復雜化，對于其他拓撲結構，本文的研究方法存在局限性，有待進一步研究。并且，當光熱發電場內發電機運行狀態不同時，本文模型的適用性僅通過具體算例進行了分析，該結論的普適性也有待進一步嚴格的證明和理論分析。

附 錄

1. 線性化等效模型推導

通過圖4可得

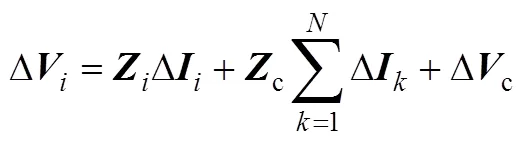
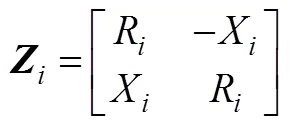
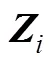
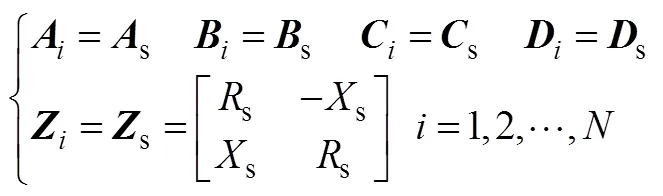
由式（16）、式（A1）、式（A2），可作差得到

再由式（16）、式（A1）、式（A2），可求和得到

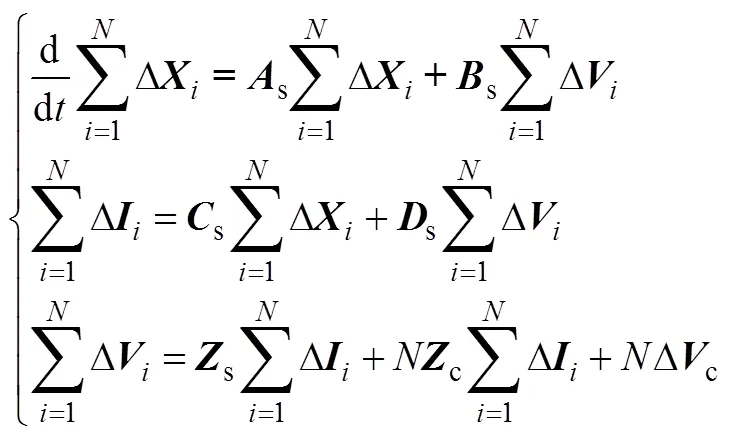
因此，可以引入新的狀態變量向量

由式（A3）和式（A5）得

由式（A4）和式（A5）得

其中

由式（A3）～式（A7）的推導表明，可以進行以下等效狀態變量變換

其中

利用式（A8）定義的等價變換，即可得到如式（18）所示的并聯光熱發電機群的狀態空間模型。

2. 非線性仿真模型

在非線性仿真中采用聚合模型時，光熱發電機的非線性模型和參數保持不變。在光熱發電機與外部電力系統之間的接口處的電壓和電流，應修改如下。

由式（A2）可得

因此，光熱發電機的輸出電流和端電壓分別為

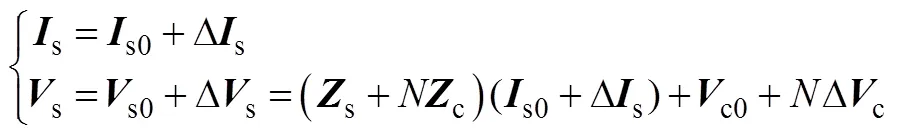
式中，下標0表示變量的穩態值。

注入外部電力系統的電流

[1] 張悅, 申彥波, 石廣玉. 面向光熱發電的太陽能短期預報技術[J]. 電力系統自動化, 2016, 40(19): 158-167.

Zhang Yue, Shen Yanbo, Shi Guangyu. Short-term forecasting technology of solar energy for concentrating solar power[J]. Automation of Electric Power Systems, 2016, 40(19): 158-167.

[2] Gil A, Medrano M, Martorell I, et al. State of the art on high temperature thermal energy storage for power generation (part1): concepts, materials and modellization[J]. Renewable and Sustainable Energy Reviews, 2010, 14(1): 31-55.

[3] 車泉輝, 婁素華, 吳耀武, 等. 計及條件風險價值的含儲熱光熱電站與風電電力系統經濟調度[J]. 電工技術學報, 2019, 34(10): 2047-2055.

Che Quanhui, Lou Suhua, Wu Yaowu, et al. Economic dispatching for power system of concentrated solar power plant with thermal energy storage and wind power considering conditional value-at-risk[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2047-2055.

[4] International Energy Agency(IEA). Technology roadmap: concentrating solar power[R]. Source OECD Energy, 2010, 7: 48-49.

[5] 邵成成, 馮陳佳, 李丁, 等. 光熱發電機群聚合模型及其在電力系統運行模擬中的應用[J]. 中國電機工程學報, 2020, 40(11): 3507-3515.

Shao Chengcheng, Feng Chenjia, Li Ding, et al. Clustered CSP model and its application in power system operation simulation[J]. Proceedings of the CSEE, 2020, 40(11): 3507-3515.

[6] 康義, 周獻林, 謝國恩, 等. 用NETOMAC程序進行電力系統動態等值研究[J]. 電網技術, 1998, 22(5): 21-24.

Kang Yi, Zhou Xianlin, Xie Guoen, et al. Using NETOMAC program in system equivalent study[J]. Power System Technology, 1998, 22(5): 21-24.

[7] 倪以信, 陳壽孫, 張寶霖. 動態電力系統的理論和分析[M]. 北京: 清華大學出版社, 2002.

[8] 胡杰, 余貽鑫. 電力系統動態等值參數聚合的實用方法[J]. 電網技術, 2006, 30(24): 26-30.

Hu Jie, Yu Yixin. A practical method of parameter aggregation for power system dynamic equivalence[J]. Power System Technology, 2006, 30(24): 26-30.

[9] 許繼剛, 汪毅. 塔式太陽能光熱發電站設計關鍵技術[M]. 北京: 中國電力出版社, 2019.

[10] 朱林, 王貝, 付東, 等. 人工魚群算法在同調發電機群聚合中的應用[J]. 電力科學與技術學報, 2020, 35(3): 61-67.

Zhu Lin, Wang Bei, Fu Dong, et al. Application of an artificial fish swarm algorithm in the aggregation of coherent generators[J]. Journal of Electric Power Science and Technology, 2020, 35(3): 61-67.

[11] 韓平平, 林子豪, 夏雨, 等. 大型光伏電站等值建模綜述[J]. 電力系統及其自動化學報, 2019, 31(4): 39-47.

Han Pingping, Lin Zihao, Xia Yu, et al. Review on equivalent modeling of large-scale photovoltaic power plant[J]. Proceedings of the CSU-EPSA, 2019, 31(4): 39-47.

[12] 蘇田宇, 杜文娟, 王海風. 多直驅永磁同步發電機并聯風電場次同步阻尼控制器降階設計方法[J]. 電工技術學報, 2019, 34(1): 116-127.

Su Tianyu, Du Wenjuan, Wang Haifeng. A reduced order design method for sub-synchronous damping controller of multi-PMSGs parallel wind farm[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 116-127.

[13] 董文凱, 杜文娟, 王海風. 弱連接條件下鎖相環動態主導的并網直驅風電場小干擾穩定性研究[J]. 電工技術學報, 2021, 36(3): 609-622.

Dong Wenkai, Du Wenjuan, Wang Haifeng. Small-signal stability of a grid-connected PMSG wind farm dominated by dynamics of PLLs under weak grid connection[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 609-622.

[14] 董文凱, 杜文娟, 王海風. 用于風電場小干擾穩定性檢驗的降階模式計算方法[J]. 電工技術學報, 2021, 36(7): 1468-1479.

Dong Wenkai, Du Wenjuan, Wang Haifeng. Reduced-order modal computation method for small-signal stability examination of a wind farm[J]. Transactions ofChina Electrotechnical Society, 2021, 36(7): 1468-1479.

[15] Zhou Y, Zhao L, Lee W J. Robustness analysis of dynamic equivalent model of DFIG wind farm for stability study[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 5682-5690.

[16] Ali M, Ilie I S, Milanovi? J, et al. Probabilistic clustering of wind generators[C]//Power & Energy Society General Meeting, Minneapolis, MN, USA, 2010: 1-6.

[17] Zou Jianxiao, Peng Chao, Xu Hongbing, et al. A fuzzy clustering algorithm-based dynamic equivalent modeling method for wind farm with DFIG[J]. IEEE Transactions on Energy Conversion, 2015, 30(4): 1329-1337.

[18] 張劍, 何怡剛. 基于軌跡靈敏度分析的永磁直驅風電場等值模型參數辨識[J]. 電工技術學報, 2020, 35(15): 3303-3313.

Zhang Jian, He Yigang. Parameters identification of equivalent model of permanent magnet synchronous generator wind farm based on analysis of trajectory sensitivity[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3303-3313.

[19] 辛煥海, 董煒, 袁小明, 等. 電力電子多饋入電力系統的廣義短路比[J]. 中國電機工程學報, 2016, 36(22): 6013-6027.

Xin Huanhai, Dong Wei, Yuan Xiaoming, et al. Generalized short circuit ratio for multi power electronic based devices infeed to power systems[J]. Proceedings of the CSEE, 2016, 36(22): 6013-6027.

[20] 辛煥海, 甘德強, 鞠平. 多饋入電力系統廣義短路比: 多樣化新能源場景[J]. 中國電機工程學報, 2020, 40(17): 5516-5526.

Xin Huanhai, Gan Deqiang, Ju Ping. Generalized short circuit ratio of power systems with multiple power electronic devices: analysis for various renewable power generations[J]. Proceedings of the CSEE, 2020, 40(17): 5516-5526.

[21] Du Wenjuan, Dong Wenkai, Wang Haifeng, et al. Dynamic aggregation of same wind turbine generators in parallel connection for studying oscillation stability of a wind farm[J]. IEEE Transactions on Power Systems, 2019, 34(6): 4694-4705.

[22] Cocco D, Serra F. Performance comparison of two-tank direct and thermocline thermal energy storage systems for 1MWe class concentrating solar power plants[J]. Energy, 2015, 81: 526-536.

[23] 馮陳佳, 邵成成, 王雅楠, 等. 考慮啟動熱量約束的光熱機組優化運行模型[J]. 電力系統自動化, 2019, 43(13): 29-35.

Feng Chenjia, Shao Chengcheng, Wang Yanan, et al. Optimal operation model of concentrating solar power units considering startup heat constraints[J]. Automation of Electric Power Systems, 2019, 43(13): 29-35.

[24] 王佳穎, 史俊祎, 文福拴, 等. 計及需求響應的光熱電站熱電聯供型微網的優化運行[J]. 電力系統自動化, 2019, 43(1): 176-185.

Wang Jiaying, Shi Junyi, Wen Fushuan, et al. Optimal operation of CHP microgrid with concentrating solar power plants considering demand response[J]. Automation of Electric Power Systems, 2019, 43(1): 176-185.

[25] Xu Ti, Zhang Ning. Coordinated operation of concentrated solar power and wind resources for the provision of energy and reserve services[J]. IEEE Transactions on Power Systems, 2017, 32(2): 1260-1271.

[26] Luo Q, Ariyur K B, Mathur A K. Control-oriented concentrated solar power plant model[J]. IEEE Transactions on Control Systems Technology, 2016, 24(2): 623-635.

[27] 關金峰, 李加護. 發電廠動力部分[M]. 北京: 中國電力出版社, 2015.

[28] IEEE Subsynchronous Resonance Task Force. First benchmark model for computer simulation of subsynchronous resonance[J]. IEEE Transactions on Power Systems, 1977, 96(5): 1565-1572.

Impact of Dynamic Aggregation of Same Concentrating Solar Power Generators in Parallel Connection on the Oscillation Stability of a CSP Plant

Lai Linchen1Zhou Qiang2Du Wenjuan1Wang Yang1Wang Haifeng1

（1. College of Electrical Engineering Sichuan University Chengdu 610065 China 2. State Grid Gansu Electric Power Research Institute Lanzhou 730050 China）

In this paper, the impact of concentrating solar power (CSP) generators in parallel connection on oscillation stability of a CSP plant is studied. It is found that the increase of the number of CSP generators in parallel connection may cause the oscillation mode associated with the excitation system of CSP generator to move to the right on the complex plane, which brings the risk of instability. Based on the Routh stability criterion, further analysis confirms and explains the mechanism of this discovery. Firstly, the linearized model of CSP generator is presented, and then the linearized model of CSP plant withCSP generators in parallel connection is established. Then, the equivalent model of CSP plant is derived with similar transformation under the condition that CSP generators are all the same. Then, the risk of oscillation instability caused by the increase of the number of parallel CSP generators is analyzed. An example shows that with the increase of the number of parallel CSP generators, the oscillation mode associated with the excitation system of the CSP plant moves to the right on the complex plane, resulting in the instability of the CSP plant. Then, the applicability of the equivalent model is discussed when the dynamic of the CSP generator is different. Finally, the theoretical analysis shows that the electromechanical oscillation mode of the CSP generator is not affected by the increase of the number of parallel CSP generators, thus proving and explaining the mechanism of the instability of oscillation mode associated with the excitation system.

Concentrating solar power (CSP) generator, dynamic aggregation, oscillation stability of power system, CSP plant

10.19595/j.cnki.1000-6753.tces.201279

TM712

甘肅省科技重大專項計劃資助項目“光熱-光伏-風電新能源基地市場消納和調度控制關鍵技術與示范應用”（19ZD2GA003）。

2020-09-23

2021-03-30

賴林琛 男，1996年生，碩士研究生，研究方向為新能源發電機動態模型和電力系統小干擾穩定性。E-mail：609795063@qq.com

杜文娟 女，1979年生，教授，博士，研究方向為電力系統穩定性分析與控制。E-mail：ddwenjuan@qq.com（通信作者）

（編輯 赫蕾）