能源互聯背景下面向高彈性的多元融合配電網雙層分布式優化調度方法研究

倪 萌 王蓓蓓 朱 紅 劉少君

能源互聯背景下面向高彈性的多元融合配電網雙層分布式優化調度方法研究

倪 萌1王蓓蓓1朱 紅2劉少君2

（1. 東南大學電氣工程學院 南京 210096 2. 國網江蘇省電力有限公司南京供電分公司 南京 210019）

能源互聯背景下，以儲能、需求響應、分布式發電（DG）等為代表的多元融合資源將深度參與電網運行。配電網作為局部地區多類分布式資源的整合者，需要通過有效的手段，對包括DG、儲能、可控負荷等多元融合的分布式資源進行優化調控，提高配電網的彈性。該文針對多元分布式資源接入后，集中式調度策略下的配電網將面臨的各類問題，結合多元分布式資源的特性，建立了面向高彈性配電網的兩層分布式協調調度模型。該文首先對高彈性配電網下的多元融合分布式資源進行協調整合，之后通過協調全局控制中心和本地控制中心，對上述資源進行合理調度，以保證在一定的電壓質量要求下消納更多的DG發電量，以提高電力中新能源的利用水平。文中算例采用IEEE 14節點和69節點的配電網系統，對比傳統集中式模型和該文提出的雙層分布式模型的優化調度結果，驗證了所提模型在配電網系統下的適用性及優越性。

多元融合分布式資源 高彈性配電網 雙層分布式調度 電壓質量

0 引言

近年來，各國不斷出臺有關政策，以鼓勵并規范分布式可再生能源的開發與利用。美國加州最先推行了可再生能源配額制，由此，風電和光伏發電從2000年5%左右的總裝機占比，逐步增加到2010年的8%，再到現如今的30%[1]。中國國家能源局在關于可再生能源發展的“十三五”規劃指導意見中鼓勵市場主體自主建設分布式發電項目，各個省份紛紛響應，其中，浙江省發改委發布的能源發展“十三五”規劃中明確了未來將建成分布式發電（Distributed Generation, DG）和光伏發電600萬kW，家庭屋頂光伏100萬戶。然而，分布式新能源發電在清潔環保的同時，還具有隨機性、波動性和可變性等特征，因此，較高的新能源滲透率可能會給電力系統運行的穩定性、電壓質量等各方面帶來挑戰[2-4]。為解決分布式發電帶來的上述問題，能源互聯網可通過物理層和信息層的互動，提高電網對于各種擾動的響應能力。作為局部地區的分布式資源整合者[5]，配電網需要通過有效的調控架構和調控策略對儲能、需求響應、分布式發電等為代表的多元分布式資源進行優化調控，從而在保證安全性、經濟性的同時，提高配電網運行彈性，支持高比例分布式新能源的接入。

當前配電網的主要調控架構包括集中式調控架構和分層調控架構。集中式調控架構是基于一個控制中心（全局控制中心），對多節點的分布式資源進行優化調度，是當前配電網采用的主要調度架構。文獻[6]針對配電網中高滲透率光伏問題，提出一種電池儲能系統參與配電網集中式調度的控制策略。文獻[7-9]通過集中優化與調度可控負荷資源實現新能源消納和削減峰值負荷的目標。文獻[10-12]考慮了多種分布式資源的接入，包括儲能和柔性負荷資源，并建立集中式聯合優化調度模型，通過算例驗證了模型的可行性。上述文獻均利用集中式調控架構，控制思路簡單，但考慮到高彈性多元融合配電網的建設需求，上述集中式調度架構存在如下兩個問題：①多元融合配電網中資源繁多，全局控制中心下控制負荷數量多[4]，需要發出大量控制指令，計算量大，計算時間長，從工程實際考慮，無法實時給出調度指令；②考慮到全局調度中心在進行控制指令下達和本地信號上傳過程中存在傳輸延遲[13]，實際系統運行時實時調度指令無法即時到達各個本地節點。

針對集中式調度模式的問題，目前已有文章指出可以通過建立分布式的分層調度架構以應對上述問題，該控制架構下，各個本地優化中心被賦予一定的自主優化權限，全局控制中心被給予更長的緩沖時間進行長時段的優化調度，不需要給出實時指令。文獻[13]考慮通信延遲與負荷預測誤差，提出保證配電網安全性和經濟性的雙層分布式儲能調度策略。文獻[14]建立了需求響應和邊緣計算的配電網分布式優化調度方法，實現配電系統能量的分區分層優化。文獻[15]提出一種交直流混合的分層分布式多元協調優化調度策略，對儲能及分布式電源進行合理優化調控。然而，由于當前文獻對配電網中各類分布式資源的特性分析不足，模型構建較為簡單，實際中執行此類優化調度結果較為困難。考慮到工程實際，現有文獻沒有更好地考慮全局控制中心和本地控制中心對于不可控負荷和多種分布式資源信息的掌握程度及預測精度的不同，以上問題可能會給調控的精確性帶來影響。此外，當前文獻中的分布式優化主要考慮了配電網的整體利益，并未兼顧配電網下本地資源擁有者的收益，例如保證儲能資源擁有者的收益盡可能增大。

針對以上問題，本文建立了面向高彈性的多元融合配電網雙層分布式優化調度模型，協調全局控制中心和本地控制中心的控制策略，對儲能及可控負荷資源進行合理優化調度。本文提出的雙層分布式框架對多元融合配電網中的儲能和需求側資源的控制更為精確，上層的負荷預測誤差由下層來協調，節約了購電成本，增加了配電網對于分布式新能源的高彈性消納能力。算例通過IEEE 14節點的配電網模型，對比集中式控制策略和雙層分布式控制策略下最終的優化結果，并通過分析新能源滲透率及全局控制中心調度周期對電網電壓偏移率的靈敏度，展現了雙層分布式控制策略的優越性。此外，為進一步驗證更為復雜的配電網下本文模型的正確性，本文最后對IEEE 69節點的配電網模型進行了集中式控制策略和雙層分布式控制策略下最終優化結果的對比分析。

1 多元融合配電網雙層分布式調度模型

傳統配電網下集中式優化調度僅有一個優化調控中心——全局控制中心，它將進行各時段負荷及新能源發電量的預測，并結合預測信息對多元資源進行優化調度。全局控制中心的調度周期，即全局周期被設定為一個較長的時間，以滿足優化計算及信息傳輸的時間要求。全局控制中心將讀取本地節點信息，對全局周期下每個時段的各類資源進行優化調度，再將相應調度指令信息下傳給本地節點。因此，集中式調度中本地節點無需進行優化，直接按上層指令對下屬各類資源進行控制。

本文為高彈性配電網設計的雙層分布式架構如圖1所示。與集中式調度不同的是，雙層分布式調度架構包含若干優化計算中心——全局控制中心與本地控制中心，兩方協同調控的指令流及信息流按照圖1進行。

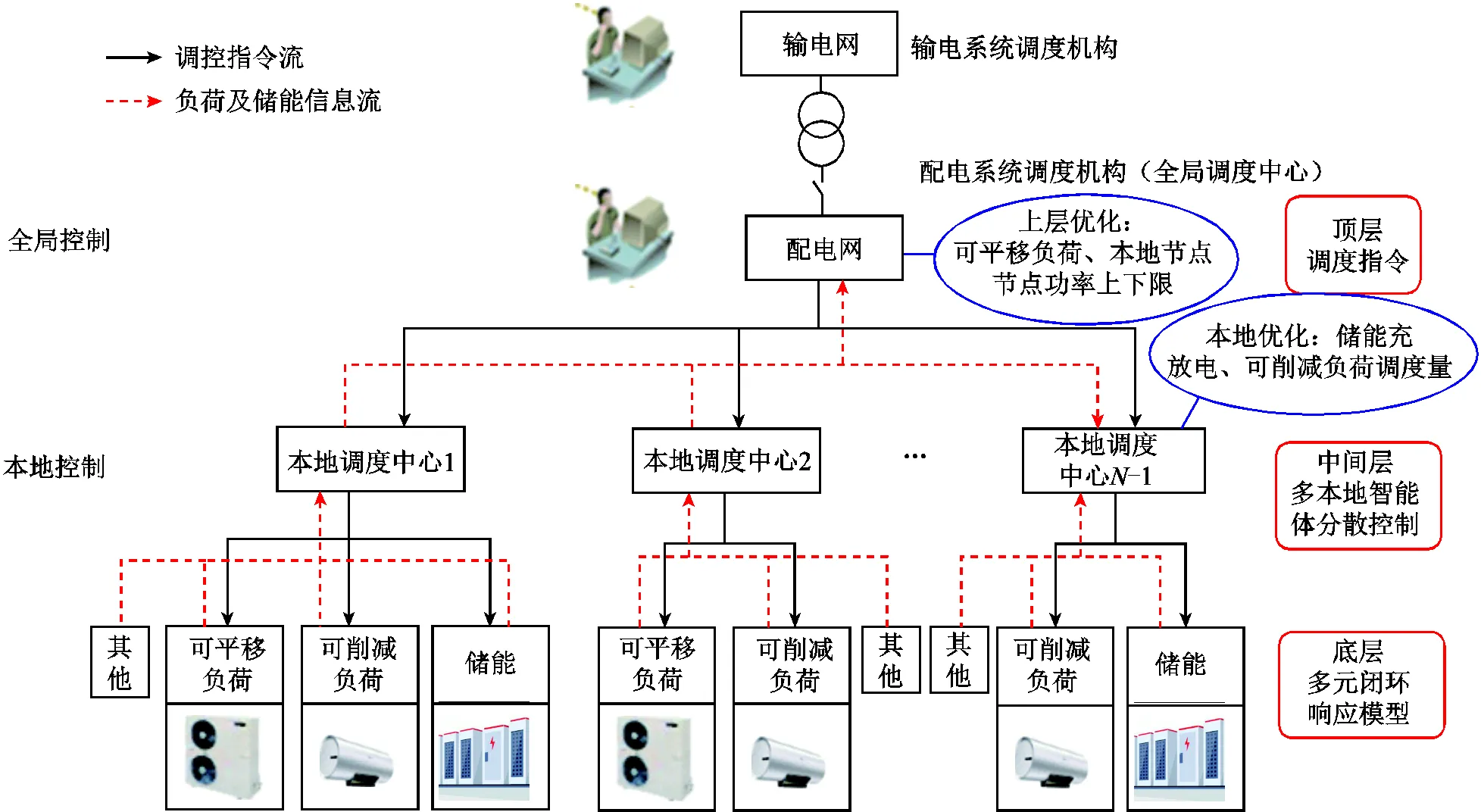
圖1 全局控制中心與本地控制中心協同控制架構

如圖1所示，本系統包括1個根節點和-1個本地節點。該框架下可進行優化調控的分布式資源包括儲能及可控負荷資源，其中，可控負荷資源包括可平移負荷及可削減負荷。雙層分布式調度架構下全局控制中心的主要任務與集中式調度框架類似。唯一區別在于，雙層分布式調度向本地控制中心傳遞的信息為可平移負荷的平移量，以及節點功率上、下限范圍約束。

本地控制中心位于本地節點，在雙層分布式調度策略下，本地控制中心讀取本地最新負荷信息及分布式發電信息，進行負荷及DG預測，之后利用預測信息，間隔一個較短的時段（本地周期）進行優化調度。由于本地控制中心下的優化調度是基于較短的本地周期下預測的負荷及分布式發電量進行的，因此，其預測精度比全局周期下的預測精度更高。在一個全局周期結束后，本地控制中心將儲能電量及負荷信息上報給全局控制中心。此外，本地控制中心所采集的信息還包括不可控負荷和分布式發電信息。

1.1 負荷及DG預測模型

本文集中式調度與雙層分布式調度兩種策略利用的負荷及新能源發電信息均為預測信息，可以通過建立季節乘積自回歸移動平均模型（Autoregressive Integrated Moving Average Model, ARIMA）預測模型獲得[16]。本文參考文獻[13]中階數的確定方式，即自回歸參數項數、差分階數、移動平均參數項數的確定方式，同時考慮負荷的日周期趨勢，建立ARIMA(3,0,3)×(3,0,3)模型為

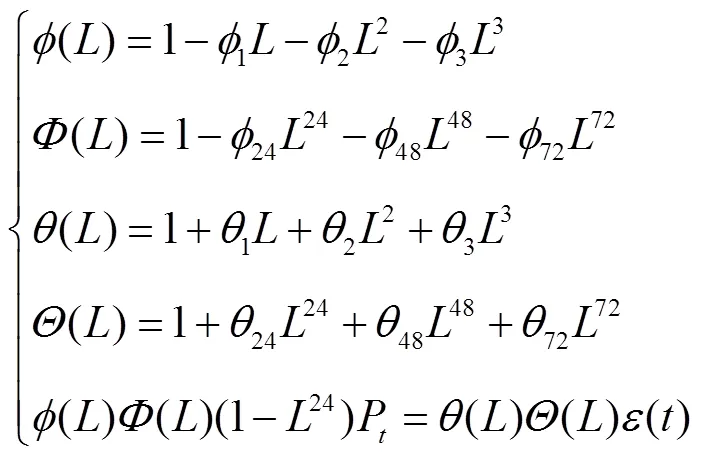
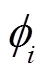
1.2 雙層分布式優化調度模型

雙層分布式優化調度模型下，首先分析高彈性配電網下多元融合的分布式資源各自的特性，從而確定協調調控策略。考慮到可平移負荷的負荷水平較高，用電時間具有連續性，調度周期較長，將其作為全局控制中心調度的資源，并將優化調度結果下達給本地控制中心。儲能靈活性較高，可削減負荷響應速度快、負荷水平較低，可由本地控制中心直接進行優化調度，并將有關結果返還給全局控制中心，方便其進行下一全局周期的優化。

為賦予本地控制中心更高的自主權，全局控制中心獲得全局周期下的最優調度結果，即各個節點各個時間點的最優凈注入功率后，需要對該功率進行松弛，并將其上、下限值下傳給本地節點，本地控制中心只需要控制本地節點凈注入功率在一定范圍內即可。因此，全局控制中心的優化分為兩個階段：第一階段是依據全局控制中心預測的負荷及DG預測量進行優化，并獲得各自擁有分布式資源節點的最優凈注入功率；第二階段是得到擁有儲能或可削減負荷資源節點的凈注入功率范圍上、下限。

本地控制中心在獲得各節點凈注入功率上下限后，利用本地節點的負荷預測信息及DG預測信息，對儲能和可削減負荷進行調用，并在一個全局周期后將最新的負荷信息和儲能的剩余電量值上傳給全局控制中心，以便其進行下一全局周期的調度，上、下層指令以及信息傳遞如圖1。

1.2.1上層全局控制中心一階段優化

上層全局控制中心一階段優化調度的基本模型與集中式優化基本相同，然而需要注意的是此階段僅確定了可平移負荷的調度結果，并為下一階段提供了各個節點最優凈注入功率值P。

一階段優化調度的目標函數為

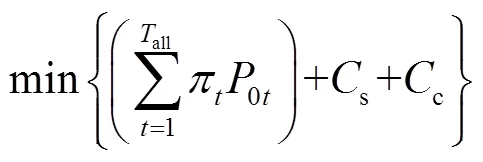
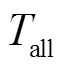
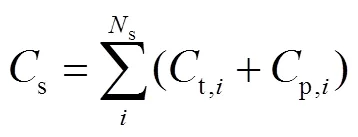
式中，s為可平移負荷的數量；p為電量補償成本；t為時間補償成本。時間補償成本可由式（4）計算得到。

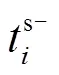
電量補償成本可由式（5）計算得到。

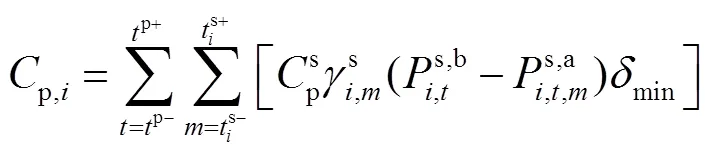
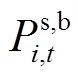
可削減負荷成本為

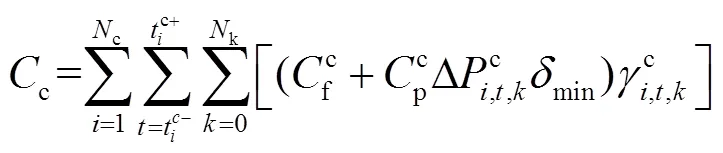
各節點的功率平衡約束方程為

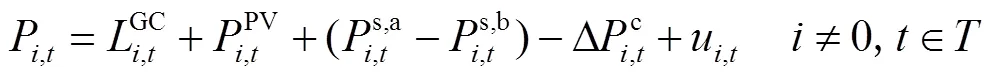
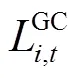
各個支路潮流方程及各節點電壓約束為

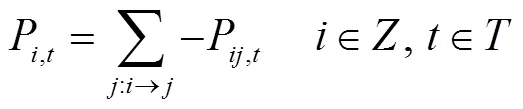
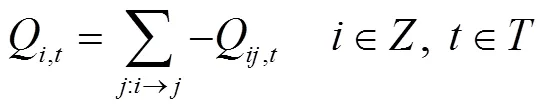
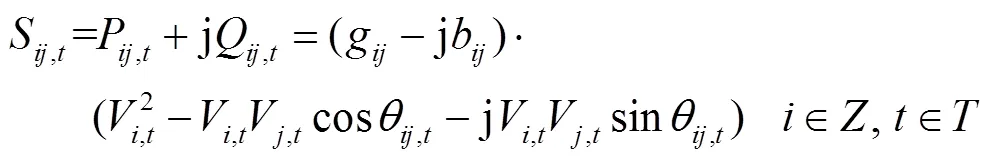
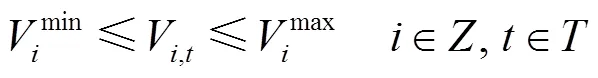
式中，為所有節點的集合；P與Q為各個節點凈注入功率；P與Q為各支路功率；S為支路-視在功率；g和b分別為支路-的電導、電納；V為時刻電壓幅值；θ為節點、之間電壓相位差；max和min分別為電壓幅值上、下限。

由于潮流方程包含的二次及三角函數等都是非凸函數，因此求解帶有潮流方程的優化問題都比較困難。本文首先進行變量替換，將非線性變量2轉換為R，VVcosθ轉換為W，VVsinθ轉換為T，然后通過二階錐松弛的方法，從而讓潮流約束轉換為線性約束加一個二階錐約束。因此，式（10）、式（11）可以轉換為式（12）～式（16）所示約束，其中，,∈，∈。

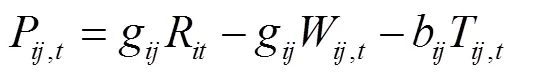
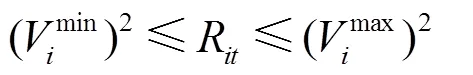
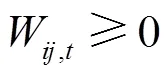
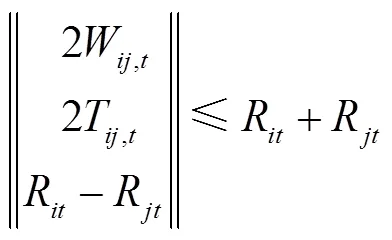
可平移負荷調度模型為

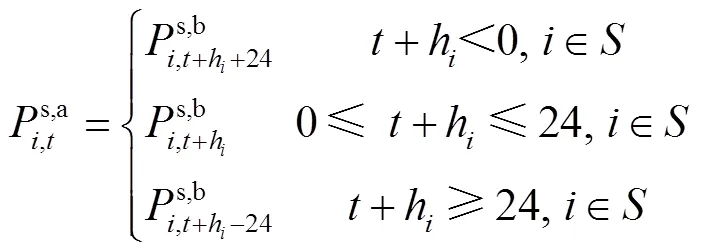
式中，為擁有可平移負荷節點的集合。

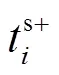
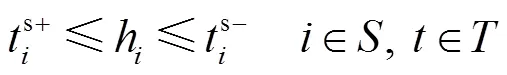
可削減負荷調度模型如式（19），通過選擇不同擋位來選擇可削減負荷調度量。

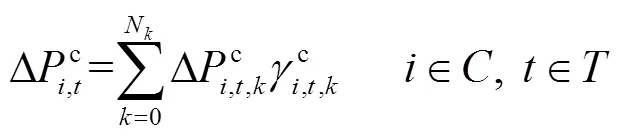
儲能的容量及充放電功率約束公式為

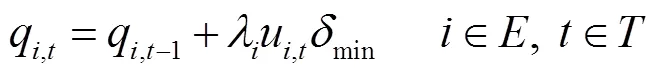
集中式優化調度模型下，儲能、可平移負荷、可削減負荷等多元融合的分布式資源全部由全局控制中心直接進行優化調度，并將控制指令下傳給本地節點，而本地節點只負責采集本地的負荷及DG信息，并根據全局控制中心下達的指令來控制多元資源的調用。因此，文中集中式模型與雙層分布式一階段優化模型基本一致。

1.2.2 上層全局控制中心二階段優化

為充分利用本地的負荷及分布式發電信息，賦予本地控制中心更大的權限，將擁有儲能或可削減負荷資源節點的最優凈注入功率值進行松弛，使得下層本地控制中心在進行優化時只需要保證節點凈注入功率在上層優化傳遞下來的上、下限范圍內即可。

針對每個包含儲能以及可削減負荷的節點，利用節點功率松弛方法[13]，獲得該節點凈注入功率的上、下邊界目標函數分別為

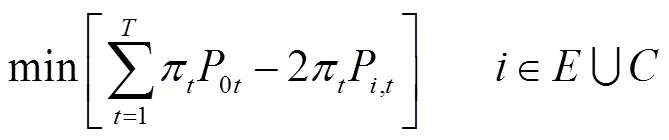
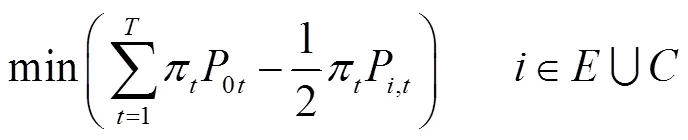
目標函數通過增大和減小需要進行松弛的節點的電價，從而使得該節點的凈注入功率在不違背約束條件的情況下盡可能地減小或增大，這里，除被松弛節點的功率及根節點的凈注入功率為可變量外，其他各節點的凈注入功率由一階段的優化結果得到。此外，二階段優化需要滿足潮流方程及電壓約束，即式（8）～式（17）。

依次對除根節點外的各個節點進行注入功率松弛，獲得各個節點的凈注入功率上、下限，分別為max、min。

1.2.3 下層本地控制中心優化及調度

擁有可平移負荷資源的節點直接執行全局控制中心關于可平移負荷的調度指令；擁有儲能或可削減負荷資源的本地控制中心從上層優化求解結果中獲得此全局周期內節點的凈注入功率上、下限，并根據最新的本地負荷及DG預測值，在每個本地調度周期內進行一次優化調度，其目標函數如式（25），即讓節點購入電量及可削減負荷調用成本之和最小化。

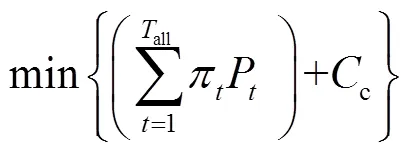
功率平衡約束方程為

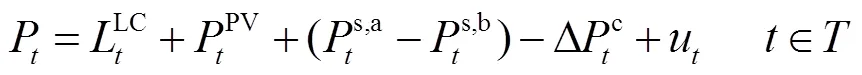
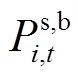
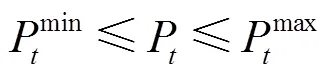
式（27）為節點功率約束。此外，需要滿足可削減負荷及儲能的約束條件，即式（19）～式（22）。

2 雙層分布式調度策略計算流程

根據1.2節對于雙層分布式框架的介紹，本文的雙層分布式調度策略仿真計算流程如圖2所示。全局控制中心首先根據本地節點傳達的最新負荷和DG信息進行預測，并進行兩階段的調度優化。一階段通過最優潮流計算獲得各節點的最優功率；二階段首先判斷該節點是否擁有儲能及可削減負荷，若有則需要對節點功率進行松弛，獲得該節點的功率上、下限值，若沒有則無需進行松弛。按順序依次對相關節點進行功率松弛，直到遍歷各個節點，跳出循環。此后，本地控制中心依據上層的調控指令及功率約束條件進行本地優化，獲得儲能及可削減負荷資源調度策略。為對比兩類優化調度策略的實際協調效果，將實際負荷和分布式發電量代入，并分別根據兩類調度策略對于分布式資源的優化結果，進行潮流計算分析。

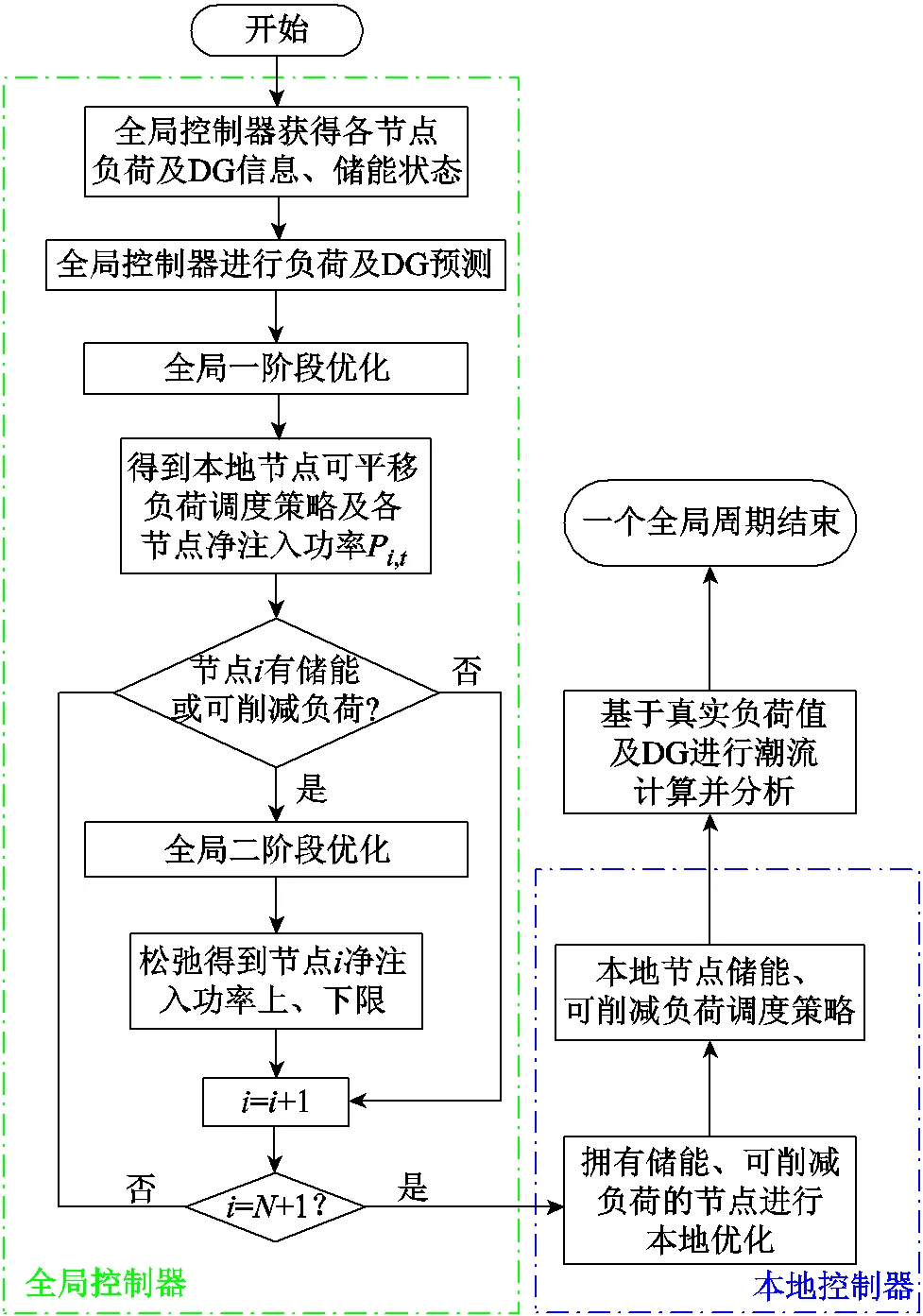
圖2 雙層分布式調度策略計算流程

3 算例分析

本文基于IEEE 14節點和IEEE 69節點的配電網系統對兩種調度模型進行對比分析，優化調度模型通過Matlab中的YALMIP[19]工具箱，并利用CPLEX[20]算法包進行求解。

3.1 算例基本參數

IEEE 14節點配電網系統拓撲如圖3所示。該配電網絡共13條支路，基準電壓為23kV，基準容量為100MV·A。

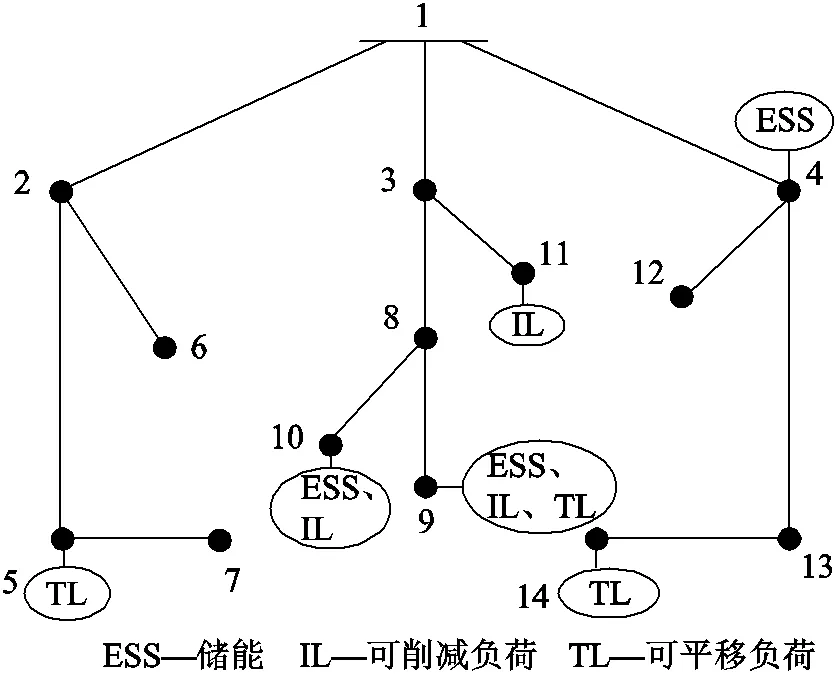
圖3 IEEE 14節點配電網系統

網絡具體參數配置如下：

（1）各節點的功率因數設為0.9，根據本節點注入的有功功率確定節點的無功功率。

（2）各節點均接入可再生能源，本文設各節點接入的新能源均為屋頂光伏，具體數據來自于pecan street網站[21]。

（3）節點4、9、10配置儲能，設系統中總的儲能滲透率為5%，儲能的容量配置計算公式為

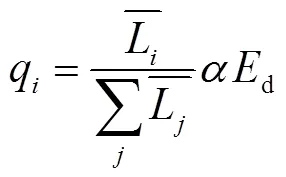
（4）節點9、10、11存在可削減負荷，其可削減負荷可調用時間及擋位配置見附表1。

（5）節點5、9、14存在可平移負荷，其基本負荷曲線見附圖1。

（6）參考江蘇省電價，將電力分為峰谷平三個時段進行計費，具體電價數據參見附表2。

（7）負荷資源調用成本參見附表3。

3.2 指標定義

兩類調度模型的結果對比需要一些衡量指標，首先定義功率曲線平滑度指標。考慮到功率曲線越平坦，電力系統越安全經濟，本文為衡量功率曲線的平坦程度引入平滑度指標，該指標越小，功率曲線越平坦，公式為

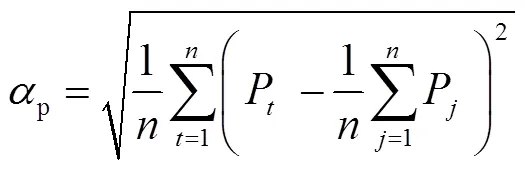
式中，P為時刻功率；為時刻點數量。

有關電壓質量的指標，這里定義各種調度策略下，各個節點調度周期內出現的最大電壓偏移的電壓偏移率為節點最大電壓偏移率，公式為

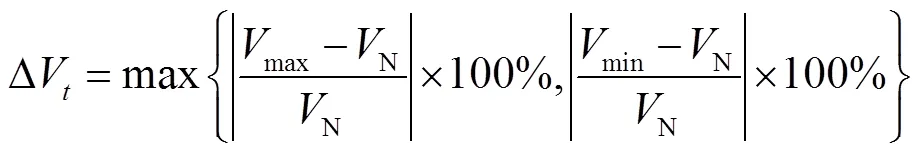
式中，N為額定電壓。

各個節點都有可再生能源發電，為衡量其在系統中的占比，本文定義新能源滲透率的計算公式為

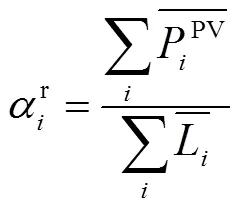
3.3 負荷及DG預測

設上層全局控制中心預測周期為24h，下層本地控制中心預測周期為1h，建立1.1節的季節乘積ARIMA預測模型，每個預測周期后利用最新的負荷或者新能源發電信息進行預測。以節點2的負荷及10%新能源滲透率下DG信息為例進行預測，本地控制中心利用的預測信息誤差明顯小于全局控制中心利用的預測信息，不同預測周期下的負荷與DG預測信息如圖4所示。

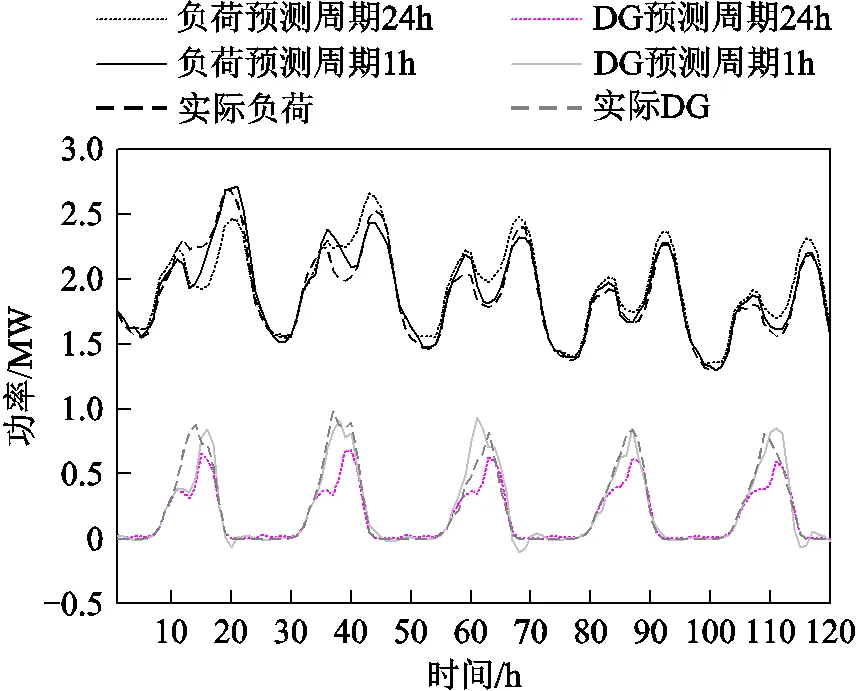
圖4 不同預測周期下的負荷與DG預測信息

3.4 兩種優化調度模型結果分析

為對比兩種調度模型的最終調度結果與最優調度結果的貼近程度，建立不考慮負荷預測誤差的最優調度模型。最優調度模型與集中式調度模型基本類似，但需滿足另外兩類條件：①不需要進行負荷預測，即各節點各個時刻的負荷提前預知，因此不存在負荷預測誤差；②不考慮信息傳輸的限制，也不需要設置本地控制中心來分擔全局控制中心的優化計算量，全局控制中心在最小的時間間隔內進行各個節點的優化調度計算。

由此，本文主要對以下三類模型進行對比分析：①參考模型：沒有預測誤差的最優調度模型；②集中調度模型：考慮預測誤差的集中式調度模型；③本文模型：本文提出的考慮預測誤差的雙層分布式調度模型。

首先，對比原根節點負荷曲線、參考模型、集中調度模型以及本文模型下的根節點功率曲線。注意，這里集中調度模型和本文模型優化調度后的根節點功率曲線的計算需要依據優化的調度結果，并結合實際負荷值而非預測負荷值進行潮流計算而得到。這里全局周期設置為24h，本地周期設為1h。

兩類模型優化調度后的根節點功率曲線如圖5所示。由圖5的折線圖可以看出，相比于原根節點功率曲線，在參考模型、集中調度模型、本文模型調度策略下，調度后根節點功率曲線峰谷差明顯縮小，由原來的11.30MW分別變為7.69MW、9.40MW、8.15MW。存在負荷預測誤差時，兩種策略下調度后最終根節點功率曲線的峰谷差大于不存在預測誤差的精確調度結果；本文模型的調度策略下，最終根節點功率曲線的峰谷差要小于集中調度模型調度策略下的峰谷差。圖5中柱狀圖分別為集中調度模型、本文模型兩種調度模式下最終根節點功率與最優調度下根節點功率的差值，可以反映出這兩種調度模式與最優調度結果的接近程度。由圖5可知，分布式雙層調度后的根節點功率更接近參考模型。

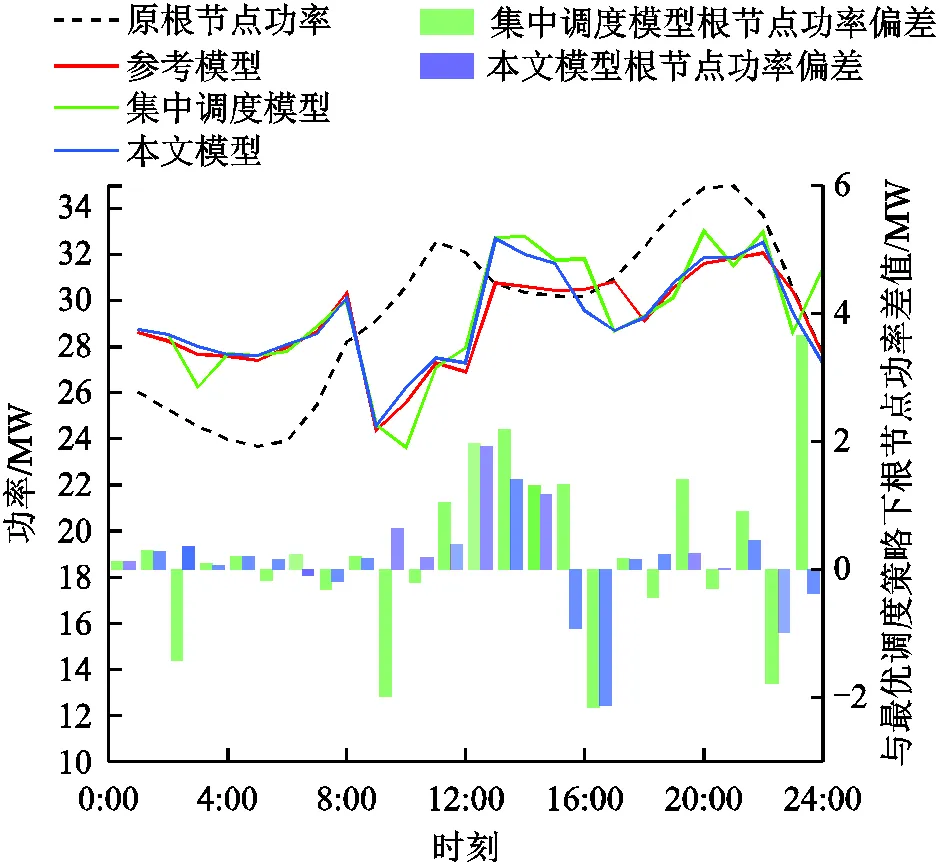
圖5 兩類模型優化調度后的根節點功率曲線

再分別計算原根節點功率曲線、參考模型、集中調度模型和本文模型調度后的根節點功率曲線平滑度指標，結果見表1，該指標越小，功率曲線越平坦。可見，兩種調度策略都可以改善根節點功率曲線的平坦程度，雙層分布式調度結果要優于集中式調度。

表1 根節點功率曲線平滑度指標

Tab.1 Smoothness index of power curve of root node

各種調度模式下購電成本及本地節點的儲能盈利見表2，集中調度與本文模型調度后各類成本及儲能盈利狀況按照相較于參考模型的費用偏差來表示。可見，參考模型、集中調度模型及本文模型調度模式下，配電網總成本均有所降低，依據參考模型進行優化調度后配電網成本最小，而本文模型下配電網的總成本小于集中調度模型。由于集中調度模型與本文模型的上層模型中利用的負荷及DG預測信息，以及關于可平移負荷的優化策略相同，可平移負荷最終調用成本相同。然而，本文模型的下層模型充分利用了下層更精確的負荷和DG預測信息進行本地優化，最終對儲能及可削減負荷的協調調度策略優于集中調度模型的優化結果。應注意，盡管依據本文模型調度后的配電網成本小于參考模型，但由于本地節點可以在功率上、下限范圍內進行本地利益最大化，擁有更大自主權，本地儲能的盈利優于參考模型，儲能運營商的利益能被更好的兼顧。

表2 三種調度模式下各類成本及盈利

Tab.2 Costs and profits under three scheduling strategies（單位：元）

為進一步分析本文模型的優化調度中，上、下層的配合關系，選取多元融合下，同時擁有儲能、可平移負荷、可削減負荷這三類資源的節點9進行分析。圖6展現了上層優化第一階段得到的節點9最優凈注入功率，負荷預測更為精確的下層優化后的節點凈注入功率，以及各類資源的優化調度量。虛線表示上層優化第二階段得到的凈注入功率上下限，可以看到，下層優化將在此范圍內優化，即滿足式（27）的限制條件。

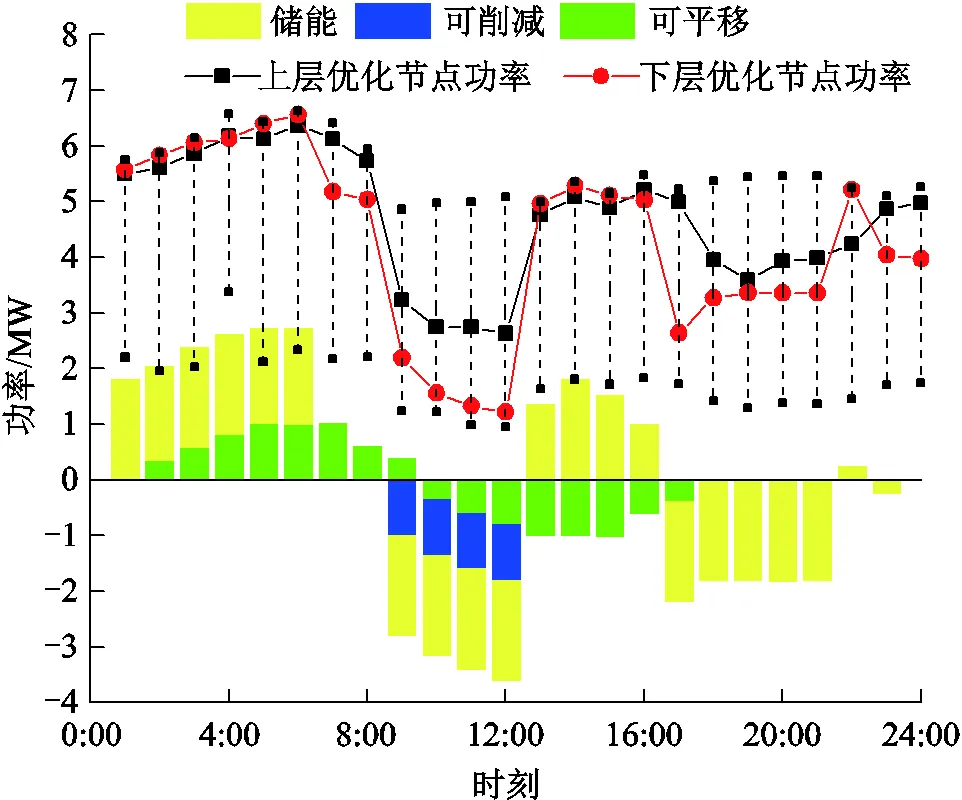
圖6 節點9優化調度結果

圖6中可平移負荷數據代表可平移負荷調度前后的功率數值差。經過上層優化，確定可平移負荷向前平移8h后，上層向下層傳遞凈注入功率的上下限，由下層再對儲能及可削減負荷進行調度。以第12小時為例進行分析，上層向下層傳遞節點注入功率的上、下限分別為最優節點注入功率的2.43～ -1.70MW之間，下層在此裕度中優化，得到最優的可削減負荷等級為第二級，即1MW，儲能放電量為1.8MW（充電為正，放電為負）。

3.5 兩種優化調度模型靈敏度分析

3.5.1 新能源滲透率對電壓最大偏移率的影響

兩種調度模式下電壓最大偏移率隨新能源滲透率的變化如圖7所示。

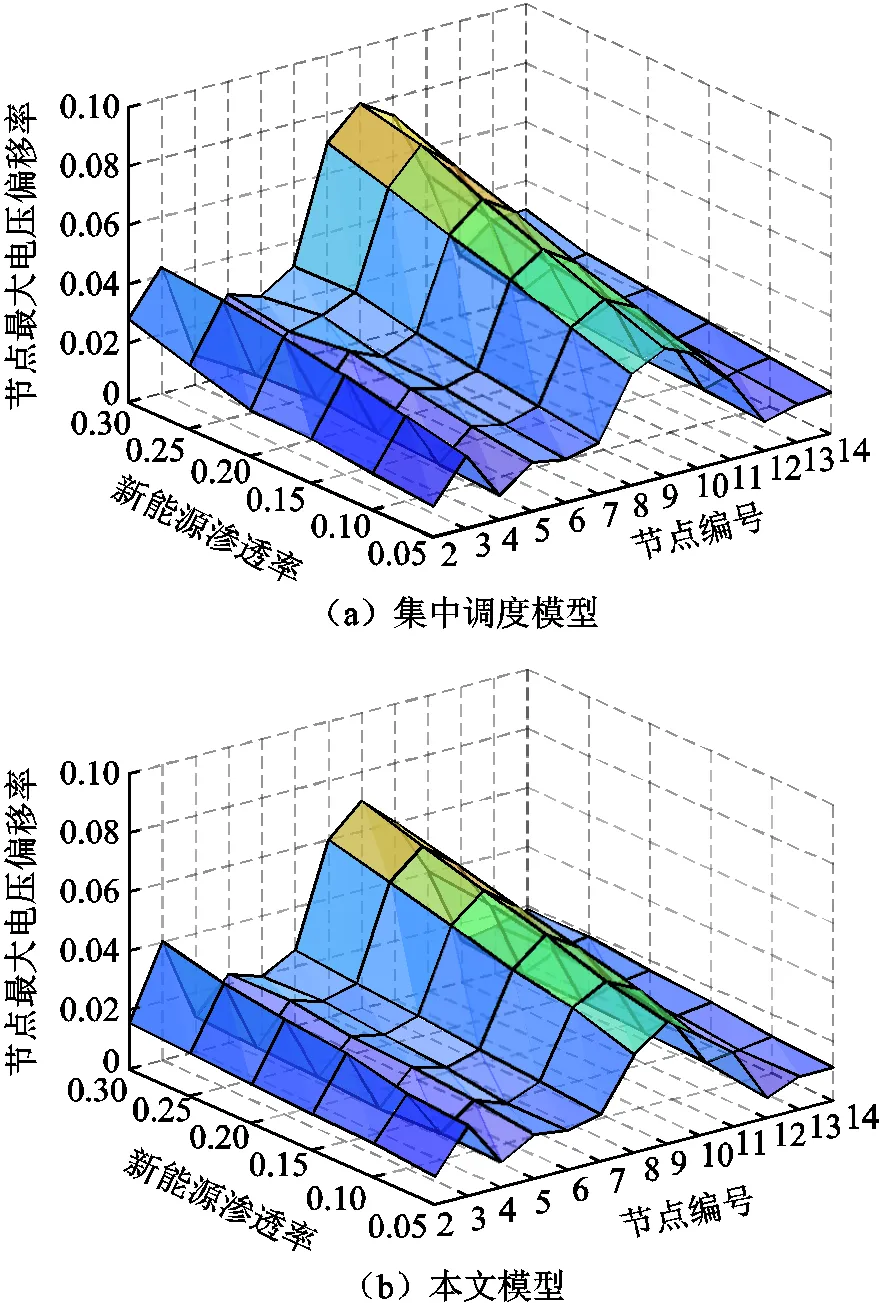
圖7 兩種調度模式下電壓最大偏移率隨新能源滲透率的變化

由圖7可以直觀看出：

（1）隨著多元融合配電網中，間歇性分布式新能源滲透率逐步增大，新能源波動范圍逐步增大，其出力的絕對預測誤差也因此增大，集中調度模型和本文模型優化調度后電壓偏移增大。

（2）可以看到帶有三類可調度資源的9節點以及相鄰的8、10節點的電壓偏移相較于其他節點更大，說明多元融合配電網中各類分布式資源接入，會影響到節點的電壓偏差，而更精確的新能源預測可以使分布式資源的調度更為精確。

（3）相比于集中調度模型的優化調度，本文模型的優化調度在DG預測誤差隨著新能源滲透率增大而增大的情況下，電壓偏移情況要優于集中調度模型，在30%的新能源滲透率下依舊保持電壓不越線（7%），原因是通過下層控制中心，可以獲得更精確的新能源發電預測數據及負荷預測數據，從而使優化更貼近于無預測誤差時的最優調度，提高了配電網對于分布式新能源接入的響應彈性。

3.5.2 全局周期時長變化下的靈敏度分析

全局周期時長是指式（2）中的常量all，表征了全局控制中心進行一次優化間隔的時長，如果變長意味著負荷及新能源發電預測周期增大。兩種調度模式下電壓偏移率隨全局周期延長的變化情況如圖8所示。

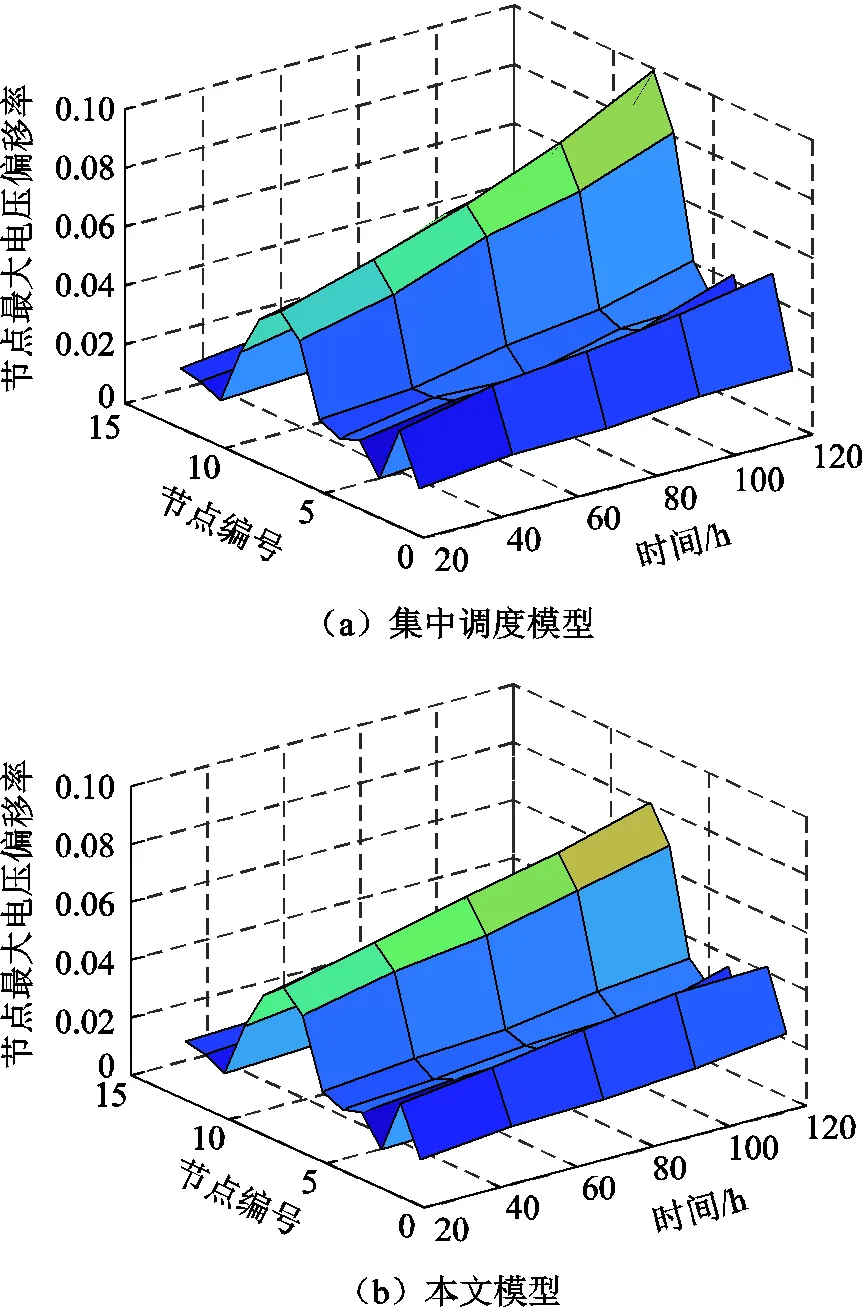
圖8 兩種調度模式下電壓偏移率隨全局周期延長的變化情況

圖8展現了所有時刻中電壓最大偏移率指標隨全局周期時長延長而變化的趨勢。全局周期以24h為單位不斷延長至120h，在集中調度模型與本文模型的優化調度策略下，全局控制中心間隔一個全局周期進行預測與優化，本文模型中本地控制中心間隔一個本地周期（1h）進行預測和優化，可以看出：

（1）隨著全局周期延長，全局控制中心下負荷預測周期因此延長，負荷預測誤差隨著負荷預測周期的延長不斷增大，對于多元融合配電網下的分布式資源的協調調度準確度下降，從而使經過集中調度模型和本文模型調度后的節點最大電壓偏移不斷增大。

（2）相比于集中調度模型，本文模型的調度策略可以在較長的調度周期下保持電壓不越線，說明分布式調度在負荷預測誤差隨著調度周期延長而增大的情況下能更精確地在減少電網成本的目標下保證電網安全。原因是本文模型通過下層控制中心，可以依據更精確的負荷及新能源發電預測數據進行優化，從而使儲能及可控負荷資源的調度更為精確。

由此可知，對于配電網中計算量更大、對時間要求更高的全局控制中心，雙層分布式調度策略提高了其對于計算周期的彈性。

3.6 69節點下兩種優化調度模型結果分析

為進一步驗證雙層分布式算法的適用性與優越性，選擇IEEE 69節點配電系統進行驗證。系統拓撲如附圖2所示，該節點網絡共69個節點，68條支路。該配電系統下各分布式資源配置見表3，其中，儲能在該系統內的滲透率為5%。

表3 IEEE 69節點配電網分布式資源配置

Tab.3 Distributed resource allocation under the IEEE 69 node distribution network

與14節點配電系統下的優化調度結果相類似，集中調度模型的調度策略與本文模型的調度策略均在一定程度上減小了根節點注入功率的峰谷差，其中，本文模型的調度策略下最終根節點功率曲線的峰谷差（3.20MW）要小于集中調度模型的調度策略下的峰谷差（2.33MW）。圖9中柱狀圖分別為集中調度模型、本文模型兩種調度模式下最終根節點功率與參考模型下根節點功率的差值，可以看出，分布式雙層調度后的根節點功率更接近于無預測誤差的最優調度結果。

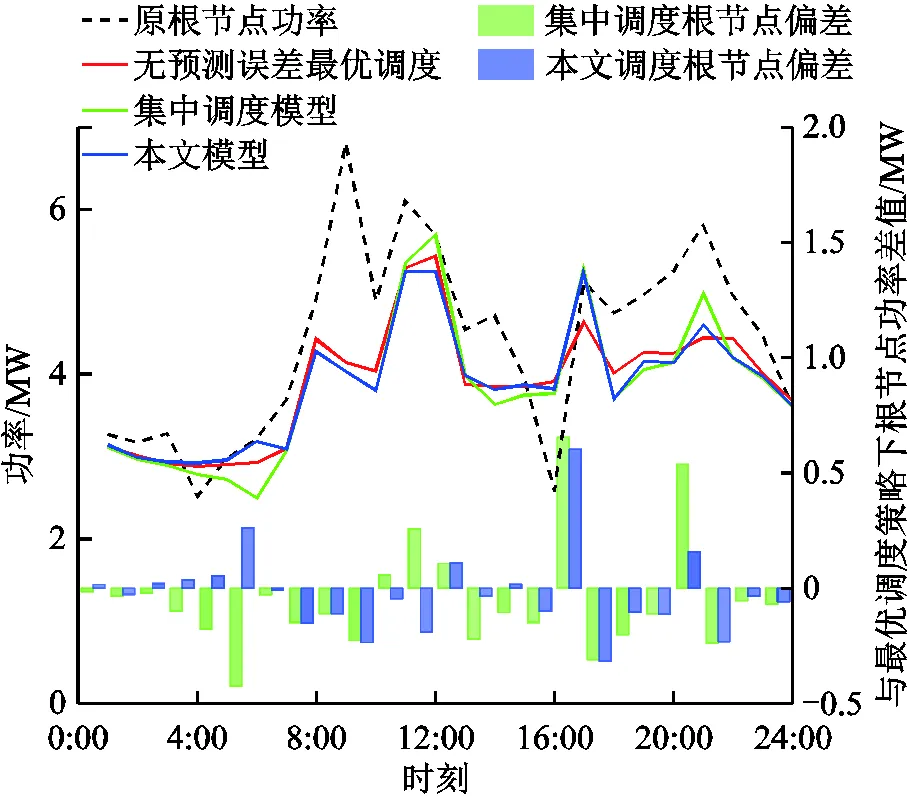
圖9 模型優化調度后的根節點功率曲線

4 結論

在當前能源互聯的背景下，本文針對高彈性配電網下多元融合的分布式資源的優化調度問題，提出一種利用儲能、可平移負荷及可削減負荷資源的雙層分布式優化調度策略。該策略充分考慮了本地節點的更為精確的負荷預測信息，通過上、下層的協調控制，對多類分布式資源進行優化，從而實現配電網成本的最小化。算例分析對比了傳統集中式調度策略及本文的雙層分布式調度結果，驗證了本文模型的可行性，同時也證明了在本文的調控模式下，配電網可以在保證較低成本的同時，獲得更為平滑的根節點功率曲線。此外，當逐步提高系統新能源滲透率或延長全局控制中心的優化周期時，本文的雙層分布式優化調度策略可以利用本地節點更為精準的負荷預測信息實現分布式資源更為精確的優化控制，提高了配電網對于分布式新能源接入的響應彈性，以及計算量更大、對時間要求更高的全局控制中心對于計算周期的彈性。

為了驗證雙層分布式模型在更為復雜的配電網系統下的適用性，本文分析了IEEE 69節點配網系統下，集中式及雙層分布式調度策略的調度結果，進一步驗證了雙層分布式調度策略的優越性。

目前研究中僅通過功率因數來限制各節點的無功功率，后續研究可以加入無功功率調節手段配合各分布式資源進行優化調度。

附 錄

IEEE 14節點算例中可平移負荷功率曲線如附圖1所示。

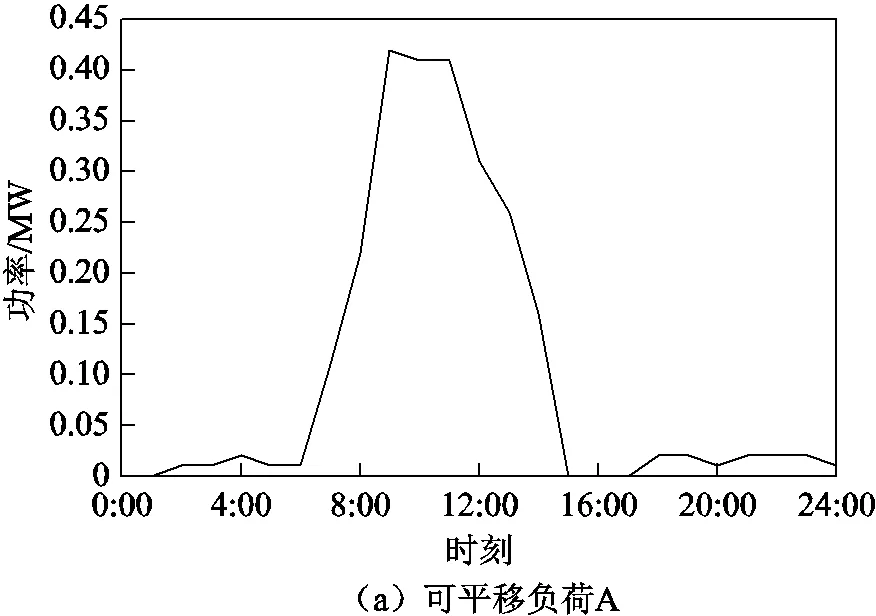
附圖1 可平移負荷功率曲線

App.Fig.1 Diagram of time-shiftable load curves

IEEE 69節點配電網拓撲如附圖2所示。可削減負荷參數配置見附表1。具體電價數據參見附表2。

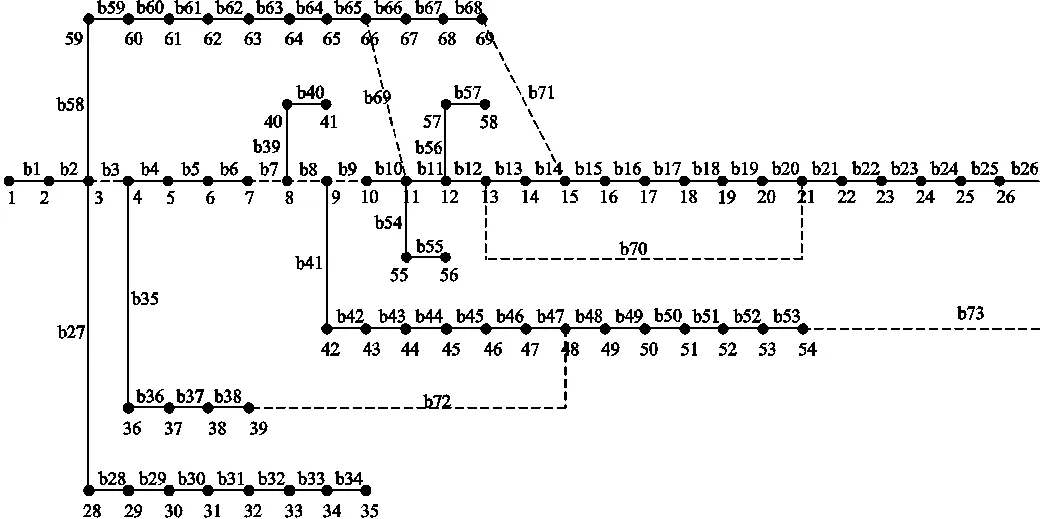
附圖2 IEEE 69節點配電網系統

App.Fig.2 Diagram of IEEE 69 node distribution network system

附表1 可削減負荷參數配置

App.Tab.1 The parameters of interruptible load（單位：MW）

節點可調用時間1檔2檔3檔 9[9, 12]0.511.5 10[6, 9]∪[17, 20]0.040.140.24 11[13, 16]0.10.250.4

附表2 配電網電價數據

App.Tab.2 The parameters of electricity price

高峰時段（8:00～12:00;17:00～21:00)平時段（12:00～7:00;21:00～24:00)低谷時段（0:00～8:00) 價格/元1077.5646.5315.5

負荷資源調用成本參見附表3。

附表3 負荷資源調用成本

App.Tab.3 The cost of controllable load resource

可平移負荷可削減負荷 CS tCS pCC fCC p 1擋2擋3擋 價格/元140482.560500650800

[1] 喻潔, 劉云仁, 楊家琪. 美國加州輔助服務市場發展解析及其對我國電力市場的啟示[J]. 電網技術, 2019, 43(8): 2711-2717.

Yu Jie, Liu Yenren, Yang Jiaqi, et al. Analysis of development of California ancillary service market and its enlightenment to China’s power market[J]. Power System Technology, 2019, 43(8): 2711-2717.

[2] 沈鑫, 曹敏. 分布式電源并網對于配電網的影響研究[J]. 電工技術學報, 2015, 30(增刊1): 346-351.

Shen Xin, Cao Min. Research on the influence of distributed power grid for distribution network[J]. Transactions of China Electrotechnical Society, 2015, 30(S1): 346-351.

[3] 孟廣雨, 于潔瀟, 楊挺. 基于隨機網絡演算的分布式能源調控系統時延上界計算[J]. 電工技術學報, 2020, 35(11): 2360-2371.

Meng Guangyu, Yu Jiexiao, Yang Ting. Upper bound calculation of delay of distributed energy resource coordinated-control system based on stochastic network calculus[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2360-2371.

[4] 高勇, 彭志煒, 劉斌, 等. 主動配電網柔性負荷優化調控研究綜述[J]. 新型工業化, 2019, 9(4): 27-34.

Gao Yong, Peng Zhiwei, Liu Bin, et al. An overview of research on optimal control of flexible loads in active distribution networks[J]. The Journal of New Industrialization, 2019, 9(4): 27-34.

[5] 吳志, 劉亞斐, 顧偉, 等. 基于改進Benders分解的儲能、分布式電源與配電網多階段規劃[J]. 中國電機工程學報, 2019, 39(16): 4705-4715.

Wu Zhi, Liu Yafei, Gu Wei, et al. A modified decomposition method for multistage planning of energy storage, distributed generation and distribution network[J]. Proceeding of the CSEE, 2019, 39(16): 4705-4715.

[6] 李佳琪, 陳健, 張文, 等. 高滲透率光伏配電網中電池儲能系統綜合運行控制策略[J]. 電工技術學報, 2019, 34(2): 437-446.

Li Jiaqi, Chen Jian, Zhang Wen, et al. Integrated control strategy for battery energy storage systems in distribution networks with high photovoltaic penetration[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 437-446.

[7] Callaway D, Hiskens I. Achieving controllability of electric loads[J]. Proceedings of the IEEE, 2011, 99(1): 184-199.

[8] 王珂, 姚建國, 姚良忠, 等. 電力柔性負荷調度研究綜述[J]. 電力系統自動化, 2014, 38(20): 127-135.

Wang Ke, Yao Jianguo, Yao Liangzhong, et al. Survey of research on flexible loads scheduling technologies[J]. Automation of Electric Power Systems, 2014, 38(20): 127-135.

[9] 寧佳, 湯奕, 高丙團. 基于需求響應潛力時變性的風火荷協同控制方法[J]. 電工技術學報, 2019, 34(8): 1728-1738.

Ning Jia, Tang Yi, Gao Bingtuan. Coordinated control method of wind farm-AGC unit-load based on time-varying characteristics of demand response potential[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1728-1738.

[10] 王林富, 邱方馳, 張斌, 等. 基于分布式電源的配電網多目標優化策略研究[J]. 智慧電力, 2019, 47(1): 47-53, 65.

Wang Linfu, Qiu Fangchi, Zhang Bin, et al. Research on multi-objective optimal strategy for distribution network based on distributed generation[J]. Smart Power, 2019, 47(1): 47-53, 65.

[11] 金國彬, 潘狄, 陳慶, 等. 考慮源荷不確定性的直流配電網模糊隨機日前優化調度[J]. 電工技術學報, 2021, 36(21): 4517-4528.

Jin Guobin, Pan Di, Chen Qing, et al. Fuzzy random day-ahead optimal dispatch of dc distribution network considering the uncertainty of source-load[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4517-4528.

[12] 葉暢, 苗世洪, 李姚旺, 等. 基于改進不確定邊界的主動配電網魯棒優化調度[J]. 電工技術學報, 2019, 34(19): 4084-4095.

Ye Chang, Miao Shihong, Li Yaowang, et al. Robust optimal scheduling for active distribution network based on improved uncertain boundary[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4084-4095.

[13] Anderson K，Rajagopal R, Gamal A. Coordination of distributed energy storage under spatial and temporal data asymmetry[J]. IEEE Transactions on Smart Grid, 2019, 10(2): 1184-1194.

[14] 彭躍輝, 韓建沛, 劉念. 考慮需求響應和邊緣計算的配電網分布式優化調度[J]. 華北電力大學學報(自然科學版), 2020, 47(4): 19-28.

Peng Yuehui, Han Jianpei, Liu Nian. Distributed optimal scheduling of distribution network considering demand response and edge computing[J]. Journal of North China Electric Power University (Natural Science Edition), 2020, 47(4): 19-28.

[15] 齊琛, 汪可友, 李國杰, 等. 交直流混合主動配電網的分層分布式優化調度[J]. 中國電機工程學報, 2017, 37(7): 1909-1917.

Qi Chen, Wang Keyou, Li Guojie, et al. Hierarchical and distributed optimal scheduling of AC/DC hybrid active distribution network[J]. Proceedings of the CSEE, 2017, 37(7): 1909-1917.

[16] 郭國太. 居民區用電負荷特性研究與模型預測[J]. 電氣技術, 2020, 21(1): 41-46.

Guo Guotai. Study on electricity load characteristic and model prediction in residential areas[J]. Electrical Engineering, 2020, 21(1): 41-46.

[17] 丁一帆. 基于價值挖掘的負荷柔性調度研究[D]. 南京: 東南大學, 2018.

[18] 符楊, 蔣一鎏, 李振坤, 等. 計及可平移負荷的微網經濟優化調度[J]. 中國電機工程學報, 2014, 34(16): 2612-2620.

Fu Yang, Jiang Yiliu, Li Zhenkun, et al. Optimal economic dispatch for microgrid considering shiftable loads[J]. Proceedings of the CSEE, 2014, 34(16): 2612-2620.

[19] Johan L. YALMIP[EB/OL]. [2020-09-30]. https: //yalmip. github. io/.

[20] IBM. IBM ILOG CPLEX[EB/OL]. [2020-09-30]. http: //www-01.ibm.com/software/integration/optimi-zation/ cplex-optimizer.

[21] Pecan Street Inc. Pecan Street[EB/OL]. [2020-09-30]. https: //www. pecanstreet. org.

Study of Two-Layer Distributed Optimal Scheduling Strategy for Highly Elastic Multi-Resource Fusion Distribution Network in Energy Interconnection Environment

Ni Meng1Wang Beibei1Zhu Hong2Liu Shaojun2

（1. School of Electrical Engineering Southeast University Nanjing 210096 China 2. Nanjing Power Supply Company State Grid Jiangsu Electric Power Co. Ltd Nanjing 210019 China）

With the development of energy interconnection system, diversified resources represented by energy storage, demand response and distributed generation(DG) are deeply involved in power grid operation. As an integrator of multiple distributed resources, distribution system needs to optimize and regulate distributed resources to improve the elasticity of distribution system. Centralized optimization strategy for the traditional distribution network has several limitations in the case of multi-resource fusion. This paper analyzes the characteristics of multiple distributed resources firstly, and then establishes a two-layer distributed optimization model for highly elastic distributed network which regulates several kinds of distributed resources through coordinating global controller and local controllers in order to ensure more DG consumption under the certain voltage quality, and to improve the utilization level of renewable energy. IEEE 14 nodes and IEEE 69 nodes distribution network systems are used for case study. The results of the two optimization strategies are compared. The applicability and advantages of the two-layer distributed scheduling model are verified.

Multiple distributed resources, highly elastic distributed network, two-layer distributed optimization model, voltage quality

10.19595/j.cnki.1000-6753.tces.201390

TM73

國家自然科學基金項目（71471036）和國網公司科技項目（泛在物聯背景下主動配電網電壓控制深度強化學習策略研究）資助。

2020-10-21

2020-11-18

倪 萌 女，1997年生，碩士研究生，研究方向為需求側管理與需求響應。E-mail：lemon1969@yeah.net

王蓓蓓 女，1979年生，副教授，博士生導師，研究方向為智能用電、需求側管理與需求響應、電力系統運行與控制和電力市場。E-mail：wangbeibei@seu.edu.cn（通信作者）

（編輯 赫蕾）