基于LSTM的飛灰含碳量預測

河北建投任丘熱電有限責任公司 李 奔 薛 峰 劉四輩

1 引言

飛灰含碳量是反映電廠燃煤鍋爐效率及經濟性的重要指標之一。飛灰含碳量的準確測量是提高鍋爐運行過程的熱轉化效率、降低發電煤耗的基礎。目前，飛灰含碳量測量方法主要分為物理測量和軟測量兩大類。主流的物理測量方法中，傳統的燃燒失重法準確性高，適用性廣但是取樣間隔長、時滯性大，難以及時反映鍋爐燃燒情況；熱重分析法自動化程度高、準確度高，但是分析時間長，設備昂貴；微波法測量速度快、精度高、儀器簡單，但是難以適應火電廠煤質多變情況，測量腔易堵灰[1]。其它物理測量方法也都面臨延時性、準確性、價格方面的問題，難以做到飛灰含碳量的實時測量。

軟測量技術是利用一些易于實時測量的，與被測量密切相關的變量，通過在線分析來估計難以測量的實時值，為飛灰含碳量測量提供了方法。在飛灰含碳量軟測量方面，多采用支持向量機（SVM）構建軟測量模型：基于數據相似度加權因子的最小二乘支持向量機（LSSVM）軟測量模型，利用雙種群差分進化算法優化模型參數的選取，通過在線評估和遞推矯正實現模型的自適應矯正[2]；萬有引力搜索算法（GSA）與LSSVM 算法相結合的GSA-LSSVM 飛灰含碳量預測模型[3]；利用主成分分析的方法優化了LSSVM 模型的輸入參數[4]；在計算樣本特征距離的基礎上，融合密度和離散度構建全局代表性指標，完成樣本的稀疏化，降低了LSSVM 模型的計算規模的同時提高了模型精度[5]；采用交叉驗證法[6]、粒子群[7]優化了SVM 模型的主要參數，并驗證了模型的準確性；采用粒子群和支持向量回歸法構建了飛灰含碳量測量模型[8]；基于LSSVM 飛灰含碳量測量裝置[9-10]。支持向量機的優勢在于具有較強的非線性映射能力，并且具有明確的數學理論支持，但是在處理多特征大規模的樣本時會耗費大量機器內存和運算時間，難以保證時效性。除支持向量機外，具有高緯非線性擬合能力的神經網絡在預測飛灰含碳量方面同樣得到了廣泛應用。文獻提出一種基于互信息選擇的神經網絡飛灰含碳量預測模型，并通過PLC 硬件實現[11]。還有基于蟻群算法優化的BP 神經網絡模型預測飛灰含碳量，和燃煤鍋爐飛灰含碳量的BP 神經網絡模型。

支持向量機、BP 神經網絡雖然具有較好的非線性映射能力，但是算法研究的對象是某一時刻的操作參數與對應時刻的飛灰含碳量。而瞬時的飛灰含碳量是一段時間內操作的綜合結果，用瞬時的操作對飛灰含碳量進行擬合更適用于穩態工況，難以滿足飛灰含碳量的動態測量要求。本文利用長短期記憶網絡（LSTM）結合灰色關聯算法構建飛灰含碳量預測模型，為飛灰含碳量動態測量提供優化方案。

2 參數選擇

2.1 數據篩選

本文使用的數據為某熱電廠350MW 機組實際運行數據。該電廠采用實驗方法測量飛灰含碳量，每天測量兩次，實測數據具有較高的準確性。選取機組一年的運行數據，參考電廠超溫超限、環保性要求，以主蒸汽溫度、SO2排放量、NOx 排放量等參數為篩選條件，除去不符合電廠安全環保要求對應的時間標簽的樣本數據。以早晚兩次飛灰含碳量取樣時間為節點，按時間標簽取主要相關參數的前半小時運行數據作為樣本數據。其中，主要相關參數數據由現場DCS 系統中直接取出，飛灰含碳量由現場實測數據錄入。主要參數及測點名稱如表1所示：

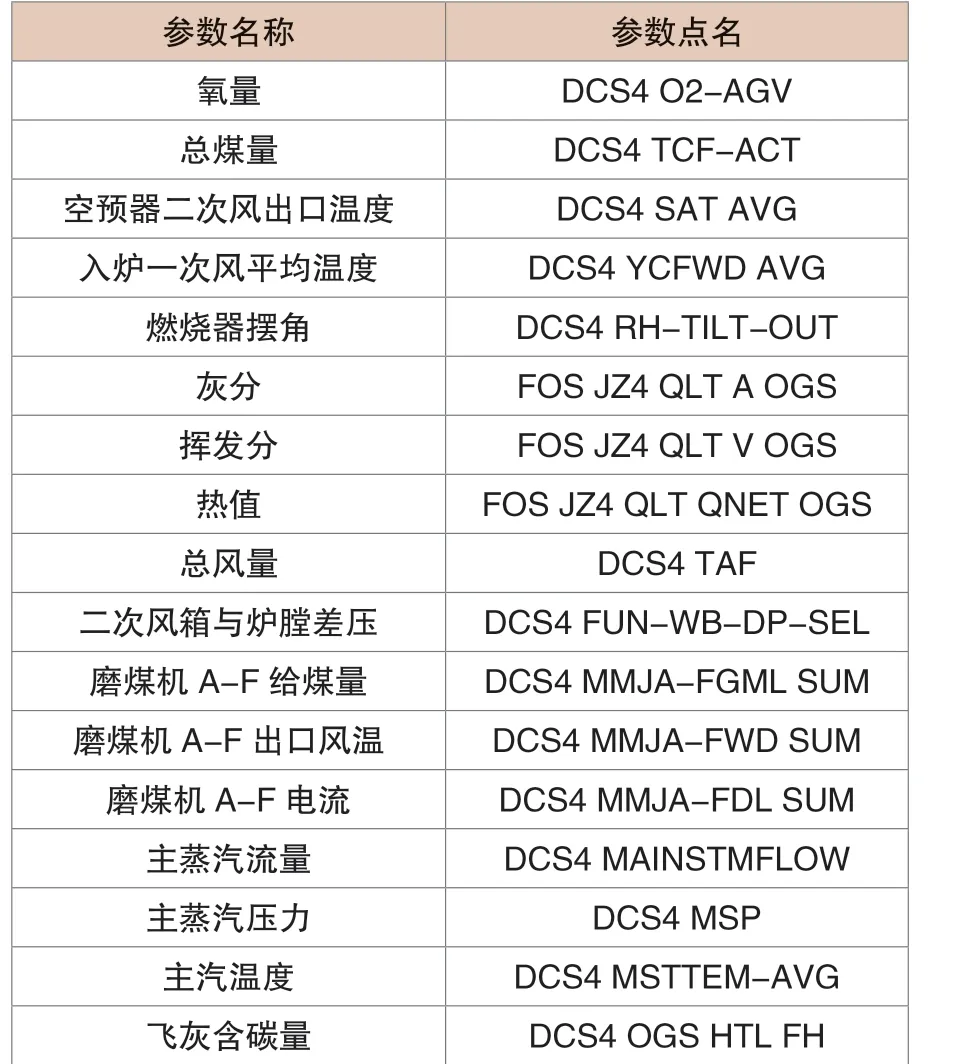
表1 主要參數及測點

2.2 飛灰含碳量影響因素分析

根據理論分析及現場實際調研，選用鍋爐汽水系統中的主蒸汽溫度、主蒸汽壓力、主蒸汽流量，風煙系統中的總風量、入爐一次風溫度、空預器出口二次風溫度、二次風箱與爐膛差壓、燃燒器擺角，制粉系統中的總煤量、煤質參數、磨煤機給煤量、電流等參數與飛灰含碳量進行相關性分析。采用斯皮爾曼等級相關系數，即spearman 相關系數進行相關性計算分析，該系數計算公式為：

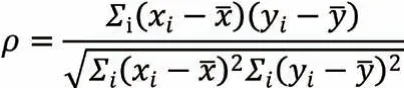
將飛灰含碳量與每一個參數進行相關性分析計算，結果如圖1所示。

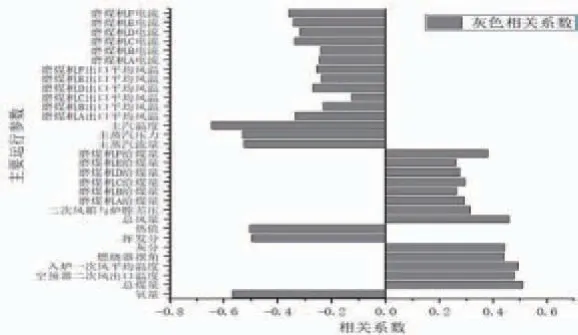
圖1 飛灰含碳量相關性因素分析

從相關性分析結果來看，汽水系統中選取的參數均與飛灰含碳量有較強的相關性。主蒸汽溫度與飛灰含碳量的關聯性最強。主蒸汽溫度主要受燃燒強度的影響，主蒸汽溫度越高，燃燒強度越大，燃盡情況越好飛灰含碳量越低。與主蒸汽溫度類似，主蒸汽壓力、流量等與鍋爐燃燒狀態直接相關的狀態參數與飛灰含碳量也有較強的相關性。

風煙系統中煙氣含氧量是評價爐內燃燒情況的重要指標，表征了爐內的氧化還原氣氛，含氧量越高煤粉燃盡越充分。總風量、二次風箱與爐膛差壓表征了爐內總配風量及二次風配風大小，在影響爐內燃燒氣氛的同時也影響了煙氣帶出熱量的多少，與飛灰含碳量具有較強的相關性。入爐一次風平均溫度體現了煤粉流在燃燒初期攜帶的熱量，影響煤粉的初期燃燒情況。一次風溫的大小取決于入爐煤的煤種，對于難燃的無煙煤、貧煤等一般采用較高的一次風溫，而此類煤種燃盡情況較差，從總體趨勢上呈現出一次風溫越高，燃盡情況越差的趨勢。燃燒器擺角決定了爐內火焰的基本形狀，進而影響燃燒狀況，影響飛灰含碳量。

制粉系統中，表征煤質信息的參數直接影響了煤粉的燃燒過程，其中熱值表征了入爐煤在爐膛內釋放的熱量，對燃燒強度起決定性作用，但是熱值越高的煤種煤化程度越高，通常燃燒特性較差，著火溫度要求高，燃盡困難。而揮發分較高的煤種燃燒特性好，易于燃盡。灰分不參與燃燒并且在燃燒過程中會吸收熱量，導致爐膛溫度降低，進而導致燃盡程度降低，飛灰含碳量升高。總煤量在總體趨勢上體現了鍋爐帶負荷的情況，總煤量越大爐內燃燒強度越高，燃燼情況越好。與總煤量類似的各層磨煤機給煤量對燃燼情況也具有較強的影響，同時呈現上下層磨煤機影響較大，中間層影響較小的趨勢。磨煤機電流一定程度上表征了磨煤機的出力情況，影響煤粉細度，與飛灰含碳量具有較強的相關性。

根據灰色相關性分析結果，最終選定氧量、總煤量、空預器二次風出口溫度、入爐一次風平均溫度、燃燒器擺角、灰分、揮發分、熱值、總風量、主蒸汽流量、主蒸汽壓力、主蒸汽溫度作為模型輸入參數，構建飛灰軟測量模型。

3 飛灰含碳量預測模型

3.1 長短期記憶網絡簡介

長短期記憶網絡（LSTM）是在循環神經網絡（RNN）的基礎上提出的時序神經網絡算法。與傳統神經網絡不同，在RNN 神經網絡中，一個序列當前的輸出與之前的輸出也有聯系。具體表現為網絡會對前面的信息進行記憶并應用于當前輸出的計算中，即隱含層之間的節點互相連接，并且隱含層的輸入包括輸入層的輸出與上一時刻隱含層的輸出。但是循環神經網絡無法解決長時依賴問題。針對這一問題LSTM 在RNN 的基礎上增加了遺忘門、信息增加門、輸出門的概念，實現長期記憶功能。在LSTM 算法中，將各種門控的結果稱為細胞記憶，細胞記憶的更新過程就是LSTM 算法訓練的過程，由各種門層的結構決定。

LSTM 算法中，遺忘門用于決定從上一時刻的細胞狀態中丟棄哪些信息。本文中選擇sigmoid 函數作為遺忘門ft的激活函數，記為σ，則忘記門表達式為：

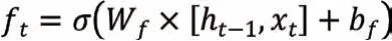
其中Wf為遺忘門的權值，bf為偏置值，ht-1為上一時刻的隱藏狀態。

信息增加門中，包括輸入門層it和候選值向量選兩值部向分量，為輸備入選門的層更it新決內定容哪。些本信文息中需選要擇更σ新，作候為的激活函數，tanh 函數作為的激活函數，則對應的表達式為：

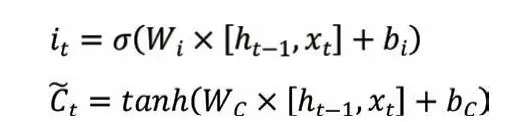
利用遺忘門和信息增加們對細胞狀態Ct進行更新：

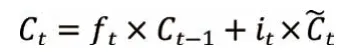
輸出門中，包括輸出ot和t 時刻的隱藏狀態ht，表達式為：

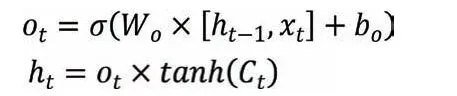
對于每一時刻，采用梯度下降法（backpropagation through time，BPTT）進行網絡的反向傳播，假設該時刻網絡的第k 個輸出參數為ok，該輸出參數的實際值為yk，則總誤差E 的計算公式為：

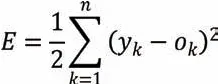
則采用梯度下降法對LSTM 網絡各層權值更新的計算公式為：

3.2 基于LSTM 的飛灰含碳量預測模型

采 用TensorFlow-2.2構 建LSTM 網 絡，對飛灰含碳量進行預測模型建模。建模使用該廠350MW 機組2020年1月至12月的實際運行數據。模型中選用sigmoid 函數作為遺忘門、輸入門層的激活函數，選用tanh 函數作為候選值向量、細胞狀態的激活函數。選用均方誤差作為模型的損失函數，選用平均誤差作為評價預測誤差的標準。模型實現過程如下：

根據電廠各系統之間的耦合關系及現場調研結果，初步選定與飛灰含碳量相關的參數；以飛灰取樣時間為基準，按時間標簽向前取半小時主要影響參數的運行數據作為時序樣本數據，對樣本數據進行穩定性、環保性、安全性篩選；采用灰色關聯分析模型，計算出相關參數與飛灰含碳量的關聯系數，并對參數進行篩選，得到影響飛灰含碳量的主要參數的時序樣本數據；采用Kera3.0構建基于LSTM神經網絡的飛灰含碳量測量模型：

初始化網格，設置雙層隱含層結構、損失函數、對應層的激活函數、初始化各層權值、設置初始超參數；按照時間標簽對時序樣本數據進行處理，將相同時間段內的數據與對應的飛灰含碳量測量值作為一組樣本，按照6:2:2的比例將樣本組劃分為訓練集、驗證集和測試集；利用訓練集和驗證集對網絡進行訓練，并根據訓練結果調整網格結構和超參數；利用測試集數據驗證模型的有效性與準確性。

3.3 模型訓練結果

取該廠2019年全年的運行數據的4/5作為訓練集用于模型訓練。采用交叉驗證法，將訓練集分為5個子集，每個子集均做一次測試集，其余的作為訓練集，進行交叉驗證。模型優化器選擇綜合性能較好的Adam 優化器，在學習率0.01、一階矩估計的指數衰減0.9，二階矩估計的指數衰減率0.99的情況下，以均方誤差作為模型的損失函數，對模型進行500次訓練，訓練結果顯示初始階段損失函數值下降較快，之后在震蕩中持續下降，最終在250次訓練后趨于穩定。此時飛灰含碳量的均方誤差為0.0038168，平均訓練誤差為4.17%，符合現場應用的精度要求。

4 預測模型效果驗證

圖2 LSTM 飛灰含碳量預測結果比對

從測試數據集中隨機選取50組數據，驗證模型預測效果，結果如圖3所示。從圖中可以看出，預測結果與實際測量結果吻合較好。預測樣本誤差如圖4、圖5所示，其中相對誤差均值為9.85%，最大相對誤差為23.995%，絕對誤差絕對值的均值為0.104，最大為0.4126，證明軟測量模型具有較好的預測效果。

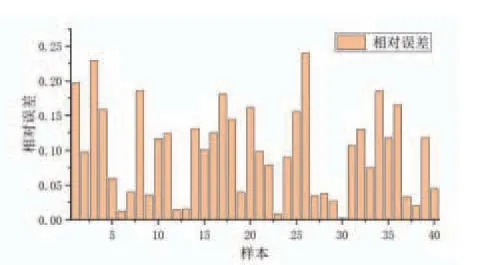
圖3 LSTM 飛灰含碳量預測相對誤差

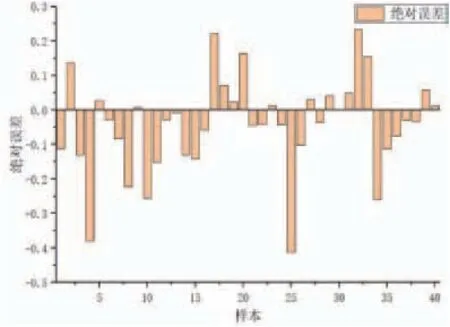
圖4 LSTM 飛灰含碳量預測絕對誤差