基于確定性規則的機電飛輪電動汽車控制策略
魏書斌,孫賓賓,李波,張錫
(山東理工大學 交通與車輛工程學院, 山東 淄博 255049)
當今世界,環境污染和能源短缺等問題日益嚴重,發展新能源汽車已成為各國節能減排的重要措施,其中,純電動汽車由于續航里程短等原因限制了發展。飛輪具有功率密度大、能量轉換快、能量轉換效率高等優點[1],因此可以將飛輪應用到汽車上,制動時將動能儲存在飛輪中,加速時將飛輪動能釋放,達到增強動力和降低能耗的效果。文獻[2]將飛輪儲能系統應用到電氣化鐵路牽引供電系統進行削峰填谷,以達到降低牽引變壓器的峰值功率,提高牽引供電系統電能質量的效果。
控制策略的優劣直接影響汽車的動力性、經濟性和駕駛性,所以控制策略是動力系統的研究重點。文獻[3]針對某功率分流式混合動力汽車,提出一種基于粒子群優化的多目標控制策略,實現降低能耗和控制電池電量的雙重目標。
本文的研究對象為機電飛輪電動汽車(electromechanical flywheel electric vehicles, EFEV),在單一鋰電池儲能系統的基礎上引入機電飛輪系統,將飛輪功率密度高和鋰電池能量密度高的特點相結合,提出機電飛輪復合儲能系統。這在節能方面具有顯著優勢,但多種工作模式也為能量管理帶來了挑戰。為了在保證動力性的基礎上提高經濟性,本文提出基于確定性規則的控制策略。
1 機電飛輪系統
以國內某MPV為原型車,在保證車輛動力性的前提下[4],將其改裝為機電飛輪電動汽車。如圖1所示,該機電飛輪電動汽車的前輪由主驅電機驅動,后輪由機電飛輪系統直接驅動。
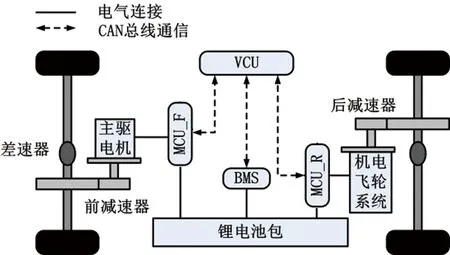
圖1 機電飛輪電動汽車構型示意圖
機電飛輪系統是一種集成飛輪、調速電機、行星齒輪機構及離合器的混合動力系統。如圖2所示,調速電機直接連接太陽輪,飛輪通過一對減速齒輪、離合器與齒圈連接,行星架則連接變速機構輸出動力至車輪。
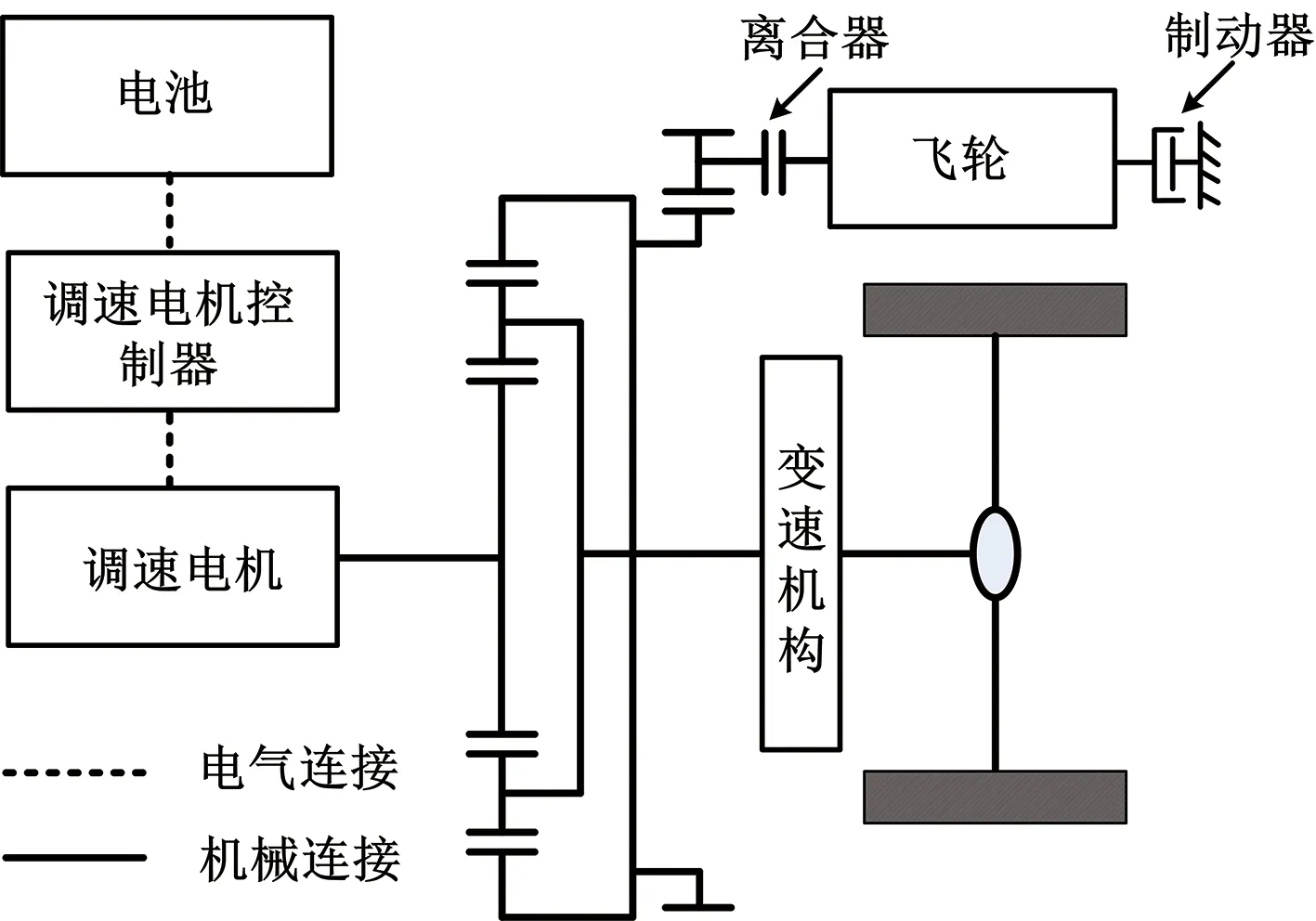
圖2 機電飛輪系統結構
由于飛輪功率密度很大,因此將其作為輔助動力源,利用飛輪瞬時大功率輸入或輸出的優勢,一方面,在滿足整車動力性的前提下,可以匹配功率更小的主驅電機,提高車輛在中低負荷工況下系統工作效率[5-8];另一方面,可以避免負載突變工況下電池會大電流充放電,進而提高能源系統工作效率并延長其使用壽命。機電飛輪系統工作模式見表1。

表1 機電飛輪系統工作模式
2 控制策略
綜合考慮整車特點,結合行駛工況,本文提出基于確定性規則的控制策略,輸入參數為車速v、加速度a、車輛需求轉矩Tdmd、電池荷電狀態SC、飛輪能量狀態SE,目的是保證主驅電機、調速電機和飛輪都可以運行在安全、高效的區域。Tin為機電飛輪系統介入轉矩;SCh,SCl分別為電池荷電狀態的上下界限;SEh,SEl分別為飛輪狀態的上下界限。
1)在起步工況下,(v<10 km/h)∩(a>0)且SC>SCl時,具體策略如下:
當Tdmd
2)在加速工況下,(v>10 km/h)∩(a>0)且SC>SCl時,具體策略如下:
當Tdmd 3)在減速工況下,a<0∩SC a)當SE b)當SE≥SEh時,同樣會出現以上4種情況,但離合器分離,而飛輪不參與制動,回收制動能量的部件只有主驅電機和調速電機。 4)在駐車工況下,v=0∩SC 當SE>0時,調速電機回收飛輪剩余能量;當SE<0時,飛輪沒有剩余能量可回收。 為保證仿真順利進行[9],采用MATLAB/Simulink建立了基于確定性規則控制策略的整車仿真模型,其能源動力系統模型如圖3所示。 圖3 能源動力系統模型 機電飛輪電動汽車采用機電飛輪復合儲能系統方案,其相關參數和動力性指標見表2和表3。原型車采用單電機直驅方案,其相關參數見表4。 機電飛輪電動汽車在行駛過程中,受到滾動阻力、空氣阻力等外力作用,其動力學方程可描述為 (1) 式中:Ft為驅動力;Ff為滾動阻力;Fi為坡度阻力;Fw為空氣阻力;Fj為加速阻力;Tt為作用于驅動輪上的轉矩;r為車輪半徑;m為整車質量;g為重力加速度;f為滾動阻力系數;α為道路坡度角;CD為空氣阻力系數;A為迎風面積;ua為車速;δ為汽車旋轉質量換算系數;du/dt為行駛加速度。 表3 機電飛輪電動汽車動力性指標 表4 單電機直驅方案相關參數 電機模型主要依據電池狀態參數及控制信號,計算并輸出電機驅動、制動轉矩[10-11],即 (2) 式中:Cd為無量綱轉矩控制信號參數,取值范圍為[-1,1],Cd大于0表示電機工作于電動狀態,Cd小于0表示電機工作于發電狀態;J為電機轉動慣量;dω/dt為電機角加速度;Tc_tem_max為基于電機溫度的峰值轉矩修正值。 根據工作狀態的不同,電機功率Pmc可以表示為 (3) 式中:Tmc為電機轉矩;nmc為電機轉速;ηmc為電機效率。 電機效率ηmc與電機轉矩和轉速有關,計算公式為 ηmc=fTmc,nmc, (4) 根據式(4),可以得到電機效率MAP,如圖4所示。 (a) 主驅電機 飛輪模型采用飛輪能量狀態SE的概念來類比化學電池的荷電狀態以研究飛輪的能量特性,計算公式為 (5) 式中:nfw為當前飛輪的轉速;nfw_max為飛輪最大工作轉速。 飛輪儲存的總動能E與轉速有關,即 (6) 式中:ω為飛輪的轉速;J為飛輪的轉動慣量,由其形狀、質量分布及轉軸位置決定,計算公式為 (7) 式中:mi為飛輪上某質點的質量;ri為質點和轉軸的垂直距離。 行星齒輪機構模型主要用于耦合轉速,已知太陽輪、齒圈、行星架分別與調速電機、飛輪、車輪直接或間接相連接。調速電機、飛輪與車輪的轉速關系為[12] (8) 式中:nwheel、nsrm、nfw分別為車輪、調速電機和飛輪的轉速;k為行星排特征參數;ifd為行星架至車輪的傳動比;ifw-r為飛輪至齒圈的傳動比。 忽略在穩定運行狀態下的能量損耗[13-15],則作用在調速電機、飛輪和車輪的轉矩關系式為 Twheel=-ifd1+kTsrm=-1+k/kifw-rTfw, (9) 式中Twheel、Tsrm、Tfw分別為車輪、調速電機和飛輪的轉矩。 電池模型主要用于估算電池荷電狀態,其計算公式為 (10) 式中:SOC0為電池荷電狀態初始值;Ib為電池電流;Ce_t_max為給定溫度下電池最大容量。 電池功率可以表示為 (11) 式中:Pb為電池功率;Eb為電池開路電壓;Ib為電池電流;Rb為電池內阻。 為了驗證控制策略的動力性,建立機電飛輪電動汽車模型并進行仿真,仿真結果見表5,結果表明機電飛輪電動汽車能夠滿足動力性要求。 表5 動力性仿真結果 機電飛輪電動汽車仿真模型以NEDC工況為研究工況,對比車速跟隨情況、電池SOC、電機高效區間工況占比、電機驅動效率,從而進行經濟性驗證[16]。如圖5所示,所構建的整車模型能夠以較高的精度跟隨NEDC循環工況車速標準值,表明了仿真模型及控制策略的有效性。由圖6可知,在NEDC工況下,機電飛輪電動汽車的SOC下降幅度較小,耗電量減少了0.89%,結果表明,相較于單電機電動汽車,采用確定性規則控制策略的機電飛輪電動汽車在經濟性方面表現更佳。 圖5 NEDC工況下EFEV仿真結果 圖6 NEDC工況電池SOC變化曲線 從圖7—圖9可以看出,在驅動階段,主驅電機、調速電機和飛輪能夠滿足整車驅動需求轉矩;在制動階段,除以上三者外,還需借助前后輪進行機械制動,滿足制動需求轉矩。仿真結果表明整車模型能夠依據控制策略實現合理的轉矩分配,滿足整車行駛需求。 圖7 NEDC工況需求轉矩曲線 圖8 電機及飛輪轉矩曲線 圖9 前后輪制動轉矩曲線 如圖10所示,在NEDC工況下,單電機直驅方案受單級變速拓撲結構的限制,單電機在某時刻不可避免地運行于低效工況域A內(中低車速、高負荷工況),整車驅動能效偏低;而機電飛輪復合儲能方案,通過控制策略控制,可實現主驅電機驅動效率優化(將原低效工況域A內單電機工況點優化到主驅電機的高效工況域B內),改善整車驅動能效。 (a) 單電機直驅 如圖11所示,NEDC工況下,相比單電機直驅方案,主驅電機的平均驅動效率提升了8.3%,調速電機的提升了3.2%。結果表明,機電飛輪復合儲能方案借助系統拓撲結構優勢,在電機驅動效率方面優于單電機直驅方案。 (a) 主驅電機與單電機效率對比圖 如圖12所示,對于單電機直驅方案而言,由于匹配的電機峰值轉矩偏大,會造成電機高效區間偏離高頻低負荷工況的問題。而調速電機驅動模式能夠顯著提升高頻低負荷工況與其高效區間的匹配度,避免出現“大馬拉小車”現象。 圖12 調速電機驅動模式工況特征規律 如表6所示,NEDC工況下,與單電機直驅方案相比,機電飛輪復合儲能系統運行于高效工況(效率>90%)的比例提升了19.9%,而工作于低效工況(效率<80%)的比例降低了13%,循環工況平均驅動效率提高了8.2%。從電機效率分布規律分析,機電飛輪復合儲能方案優于單電機直驅方案,經濟性能更佳。 表6 NEDC工況下不同方案電機效率分布規律 本文以機電飛輪電動汽車為研究對象,采用基于確定性規則的控制策略,建立機電飛輪電動汽車模型并進行仿真,通過對比仿真結果,得到以下結論: 1) 該機電飛輪電動汽車按照本文提出的控制策略能夠滿足動力性要求,實現合理的轉矩分配,滿足實際轉矩需求。 2) 與單電機直驅方案相比,機電飛輪復合儲能方案能夠顯著提升循環工況與電機高效區間的匹配度,有效提高系統驅動效率,降低耗電量。 3) 通過仿真證明,本文制定的控制策略能夠保證機電飛輪電動汽車在滿足動力性的基礎上提高經濟性。3 仿真建模
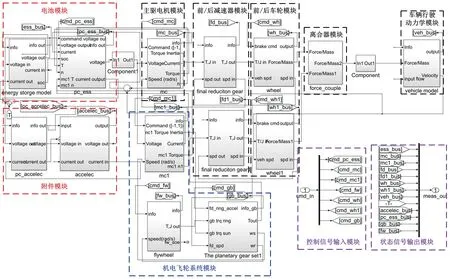
3.1 車輛縱向動力學模型


3.2 電機模型
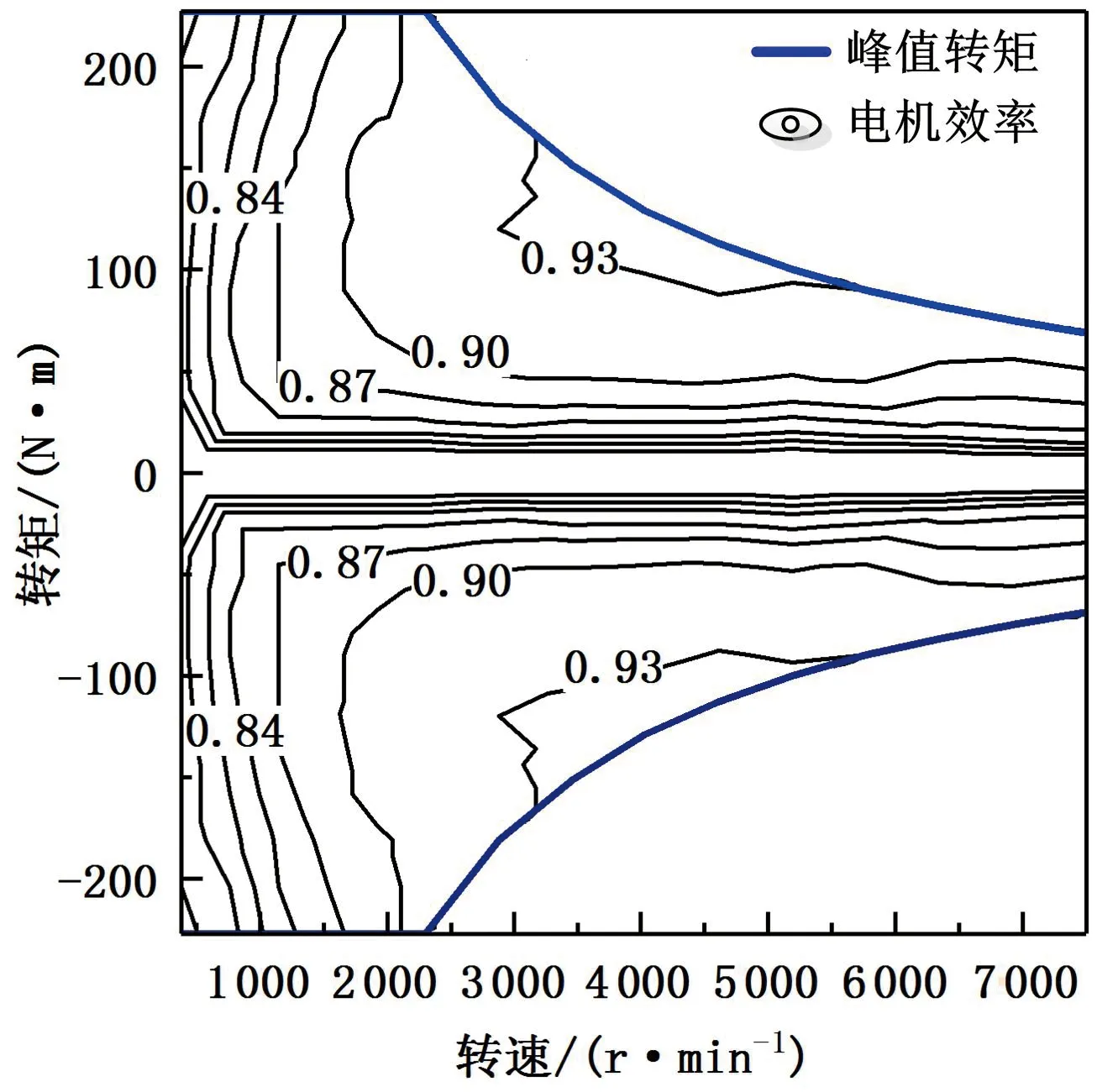
3.3 飛輪模型
3.4 行星齒輪機構模型
3.5 電池模型
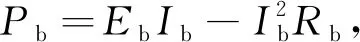
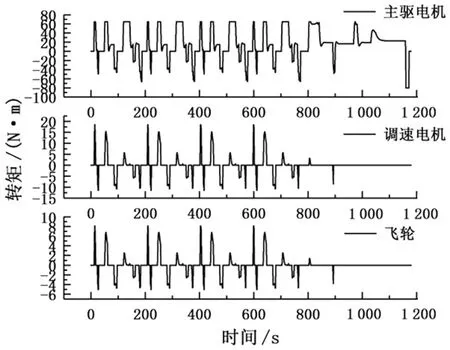
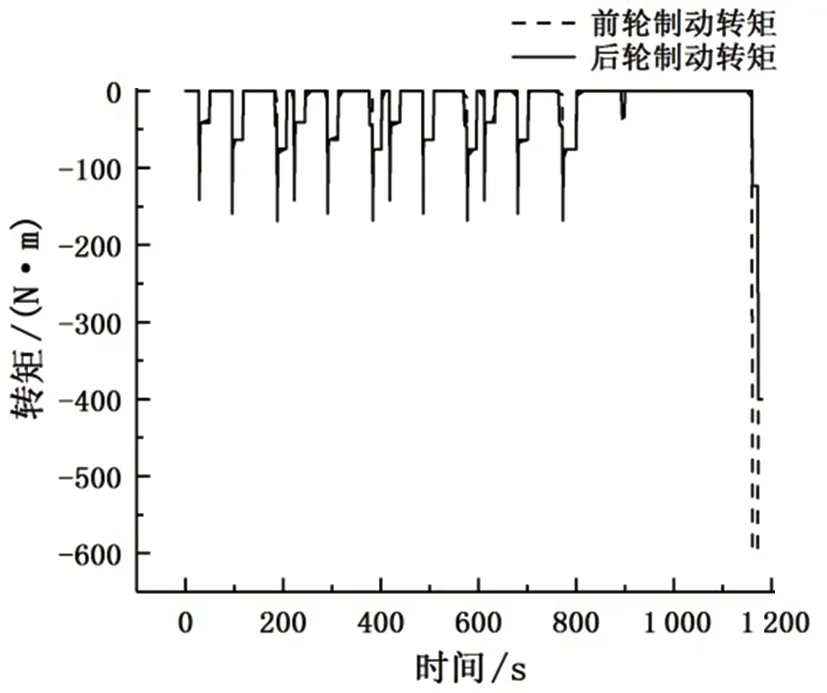
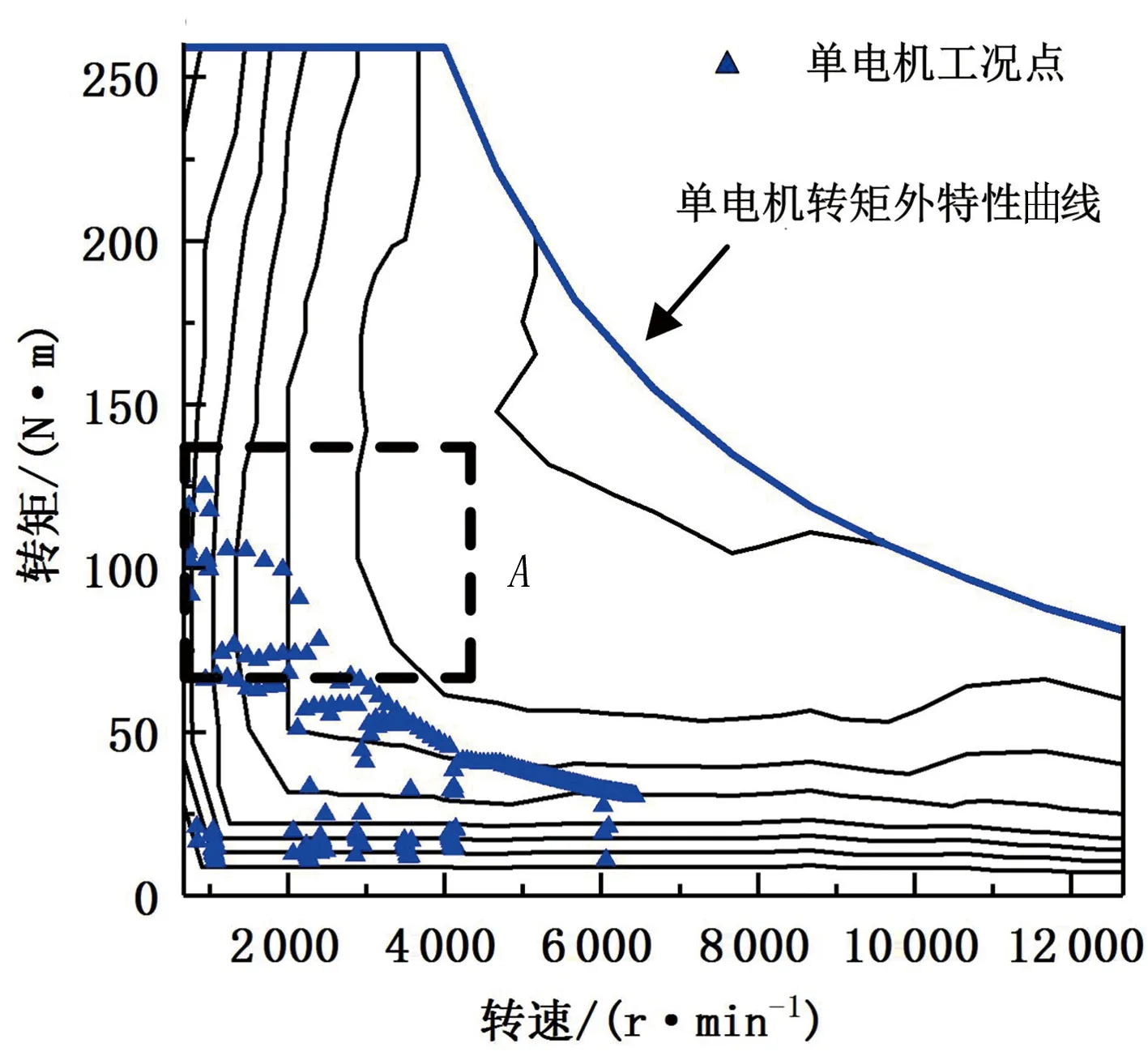
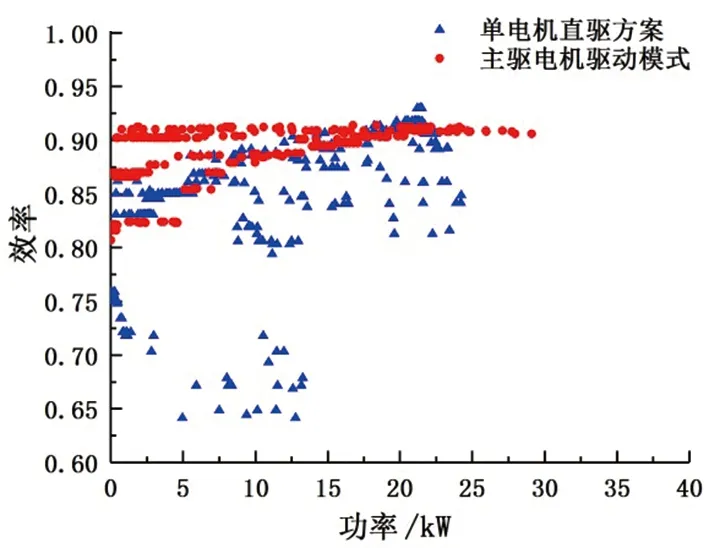
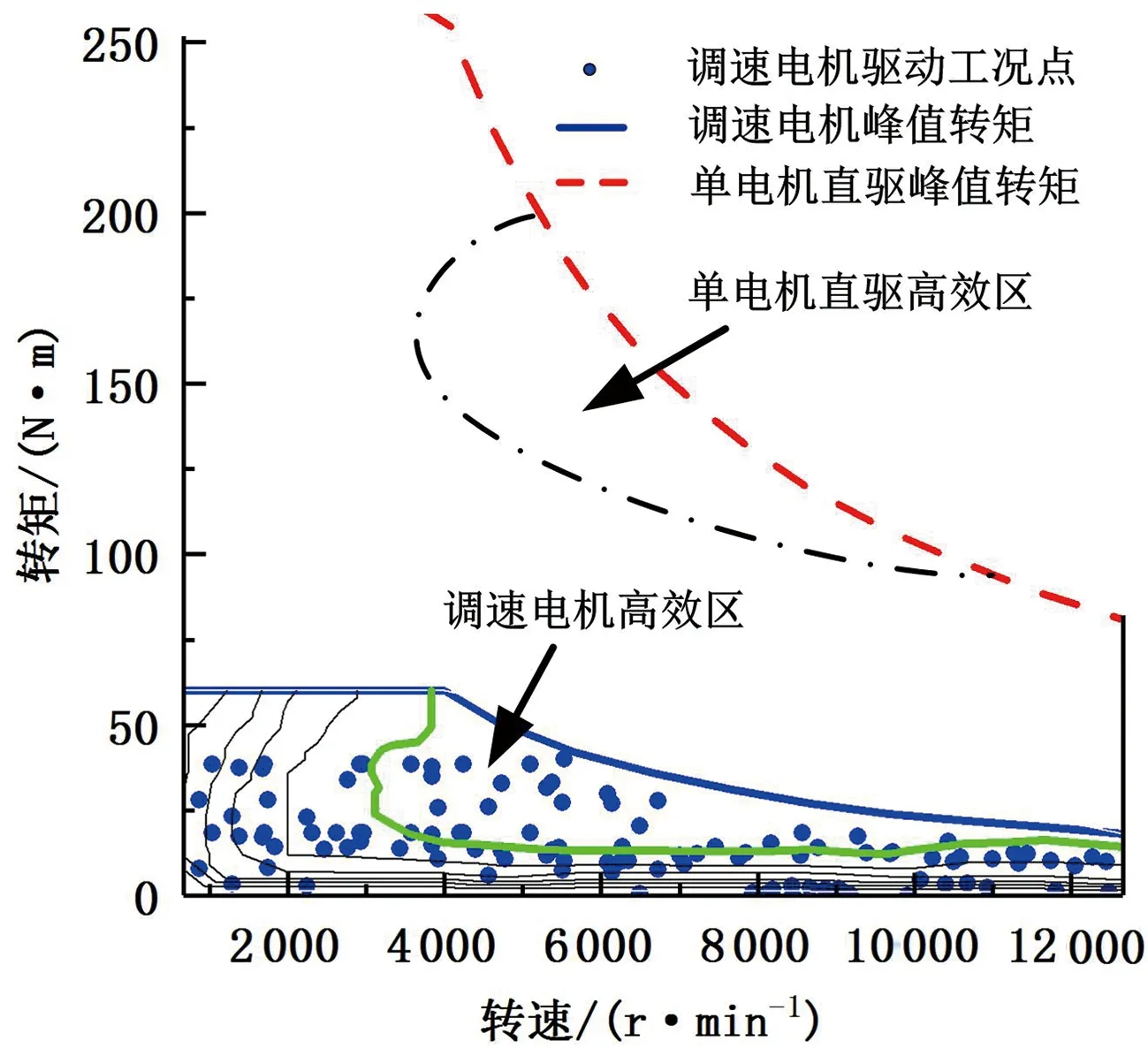
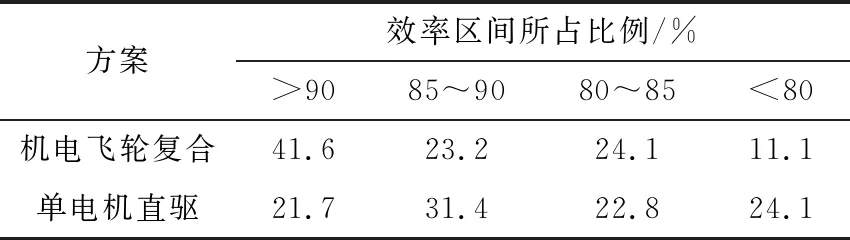
4 仿真分析

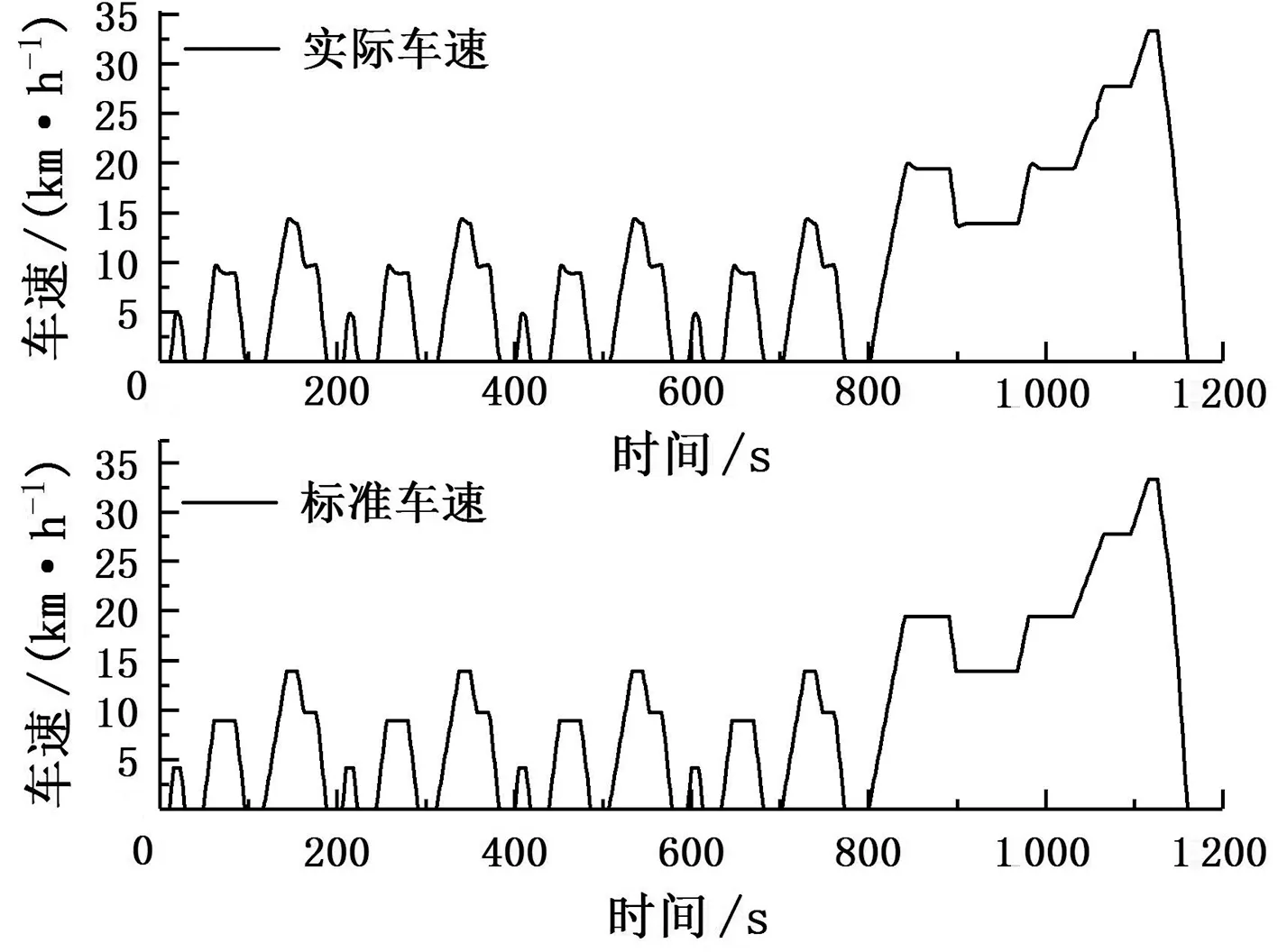
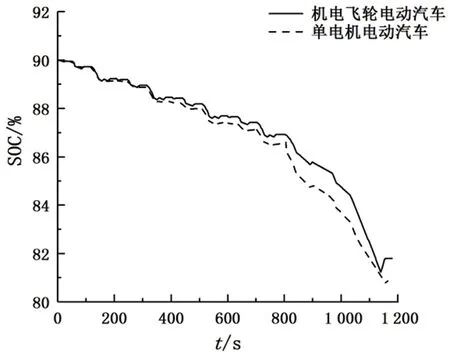
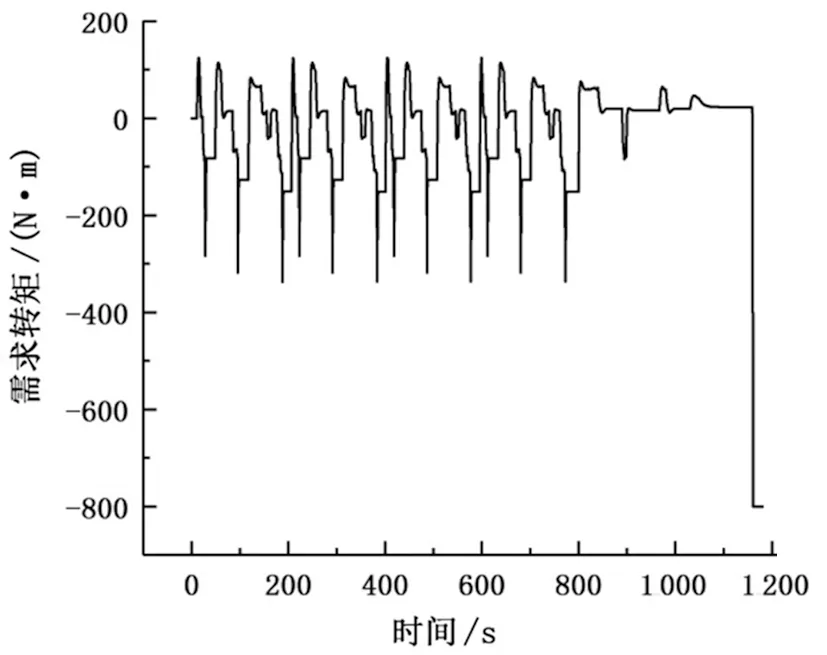
5 結論

