高海拔環(huán)境下離心風機性能數(shù)值模擬研究*

劉 學，劉 劍，王 東

(1.遼寧工程技術大學 安全科學與工程學院，遼寧 葫蘆島 125105；2.遼寧工程技術大學 礦山熱動力災害與防治教育部重點實驗室，遼寧 葫蘆島 125105)

0 引言

我國青藏高原地區(qū)平均海拔4 000 m以上，蘊藏著豐富的礦產(chǎn)及地熱資源，號稱中國的“銅墻鐵壁”[1-3]。隨著海拔的升高，低壓、缺氧、寒冷干燥等氣候環(huán)境極大程度影響著電氣機械設備的正常運轉(zhuǎn)。離心風機作為重要的通風、排塵及冷卻設備，廣泛應用于工廠、礦井及隧道等場景。由于高海拔環(huán)境下離心風機性能指標異于出廠時的性能指標，所以經(jīng)常導致其出現(xiàn)動力不足現(xiàn)象[4-5]。因此，準確評估離心風機在高海拔環(huán)境下運行時的性能參數(shù)變化規(guī)律是必要的。

受高海拔特殊地理氣候條件限制，迄今為止，國內(nèi)外有關高海拔環(huán)境下離心風機性能的研究鮮有報道，理論分析是主要研究方法。陳霞等[6]闡述了高海拔地區(qū)大氣壓力、溫度和空氣密度特點并對高海拔地區(qū)卷煙廠卷接機組的高壓離心風機性能進行了理論分析，指出了高海拔離心風機的風量、風壓及功率等參數(shù)與海平面地區(qū)的不同。此外，在高海拔礦井及隧道用軸流風機性能研究方面，1978年趙梓成等[7]首次通過理論分析和現(xiàn)場試驗對海拔高度分別為1 350，1 720，1 920和2 880 m運行環(huán)境下的JBT-52-2型局部通風機性能進行了研究，結(jié)果表明，通風機轉(zhuǎn)數(shù)不變時，其風量與海拔高度無關，而壓力與海拔高度成反比；王峰等[8]利用相似率原理對高海拔特長公路隧道施工風機的風壓和功率修正系數(shù)進行了推導，得到的計算公式用于指導雀兒山隧道的風機選型；宋品芳等[9]基于熵權模糊法對高海拔礦井風機性能的影響因素進行了理論分析。在國外，有關離心風機性能的研究大多基于平原環(huán)境條件。 Bayomi等[10]為消除進氣畸變，在離心風機的進氣道中使用矯直器，通過實驗探討了該方法對離心風機性能的影響；Gholamian等[11]通過數(shù)值和實驗方法分析了進口噴嘴與葉輪軸向間隙對離心通風機效率和流型的影響；Mario等[12]提出1種有效相似性的假設，使葉輪修整后離心泵的效率得到提升。

綜上所述，雖然國內(nèi)外眾多學者在離心風機性能方面開展了較多研究，但隨著海拔的升高，大氣壓力降低，空氣含氧量減少，有關高海拔環(huán)境下的離心風機性能研究卻較少，且研究大多集中在理論分析方面。因此，以9-26-4A型高壓離心風機為例，通過對不同海拔高度環(huán)境下風機流場的數(shù)值模擬，探尋高海拔環(huán)境下的風機性能參數(shù)變化規(guī)律，得到海拔高度與離心風機各項性能參數(shù)的定性及定量關系，為保證高海拔地區(qū)離心風機的高效運轉(zhuǎn)及風機選型提供理論參考。

1 數(shù)值模型的建立和求解

1.1 物理模型

本文研究對象為9-26-4A型高壓離心風機，圖1(a)為風機整體裝配圖。其主要結(jié)構(gòu)參數(shù)見表1。利用SolidWorks軟件采用1∶1比例建立該風機三維仿真模型，如圖1(b)所示。

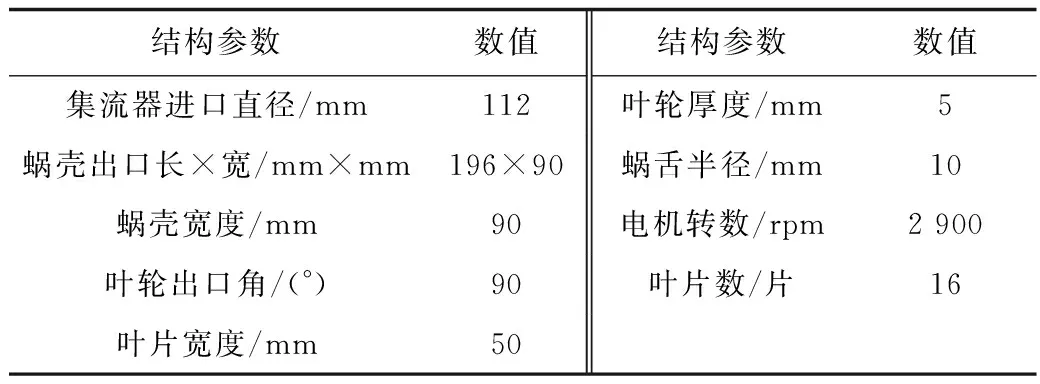
表1 風機主要結(jié)構(gòu)參數(shù)Table 1 Main structural parameters of fan

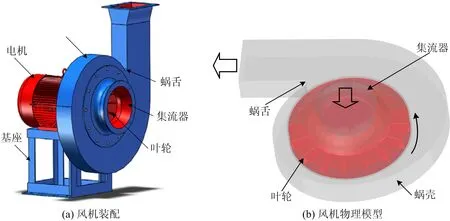
圖1 9-26-4A型離心風機Fig.1 9-26-4A centrifugal fan

1.2 網(wǎng)格劃分及獨立性檢驗

針對離心風機計算域內(nèi)復雜幾何結(jié)構(gòu)，劃分網(wǎng)格時采用非結(jié)構(gòu)化四面體單元分塊生成計算網(wǎng)格，并采用分區(qū)和局部加密劃分方法，在葉輪轉(zhuǎn)動區(qū)采用密集網(wǎng)格，在集流器入口及蝸殼出口區(qū)采用稀疏網(wǎng)格。為滿足計算精度要求，將模型劃分為8組不同數(shù)量的網(wǎng)格，并對常壓環(huán)境下風量為2 190 m3/h工況時的風機模型進行數(shù)值計算，監(jiān)測風機模型全壓及軸功率，驗證網(wǎng)格獨立性。如圖2所示，當網(wǎng)格數(shù)超過452萬時，風機全壓值和軸功率幾乎不再發(fā)生變化。因此，本文最終使用452萬網(wǎng)格進行模擬計算。網(wǎng)格劃分結(jié)果如圖3所示，其中，圖3(a)為模型整體網(wǎng)格，圖3(b)為風機葉輪及蝸舌附近的網(wǎng)格放大圖。

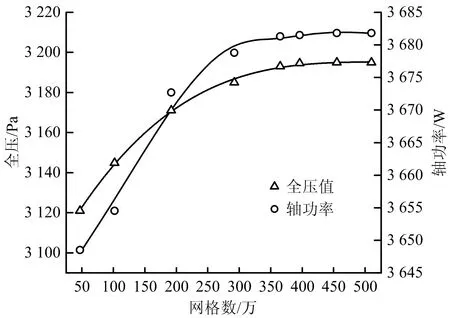
圖2 網(wǎng)格獨立性檢驗Fig.2 Grid independence test

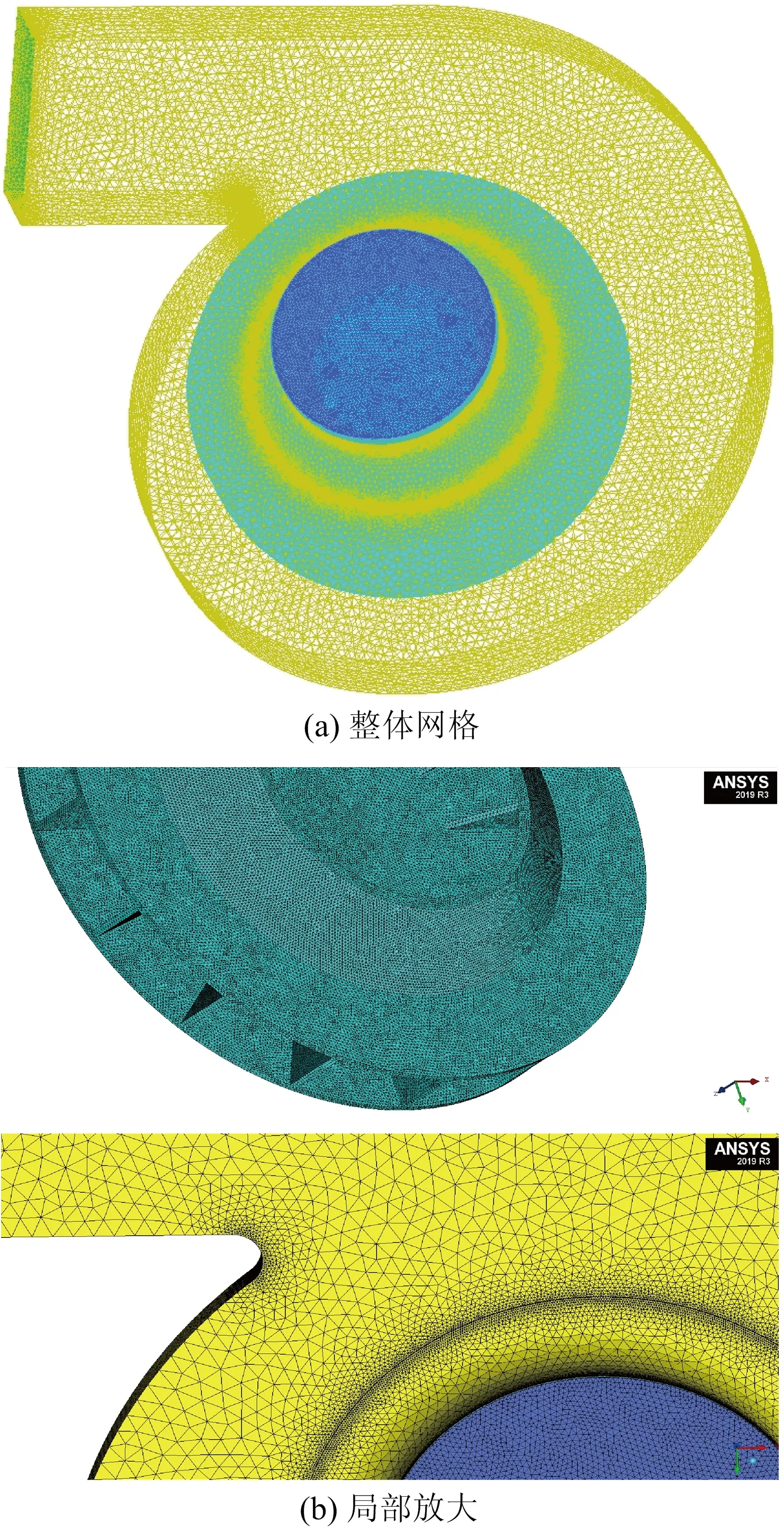
圖3 風機模型網(wǎng)格Fig.3 Fan model grid

1.3 數(shù)值計算方法及參數(shù)設定

利用ANSYS FLUENT軟件對風機模型進行三維定常模擬，數(shù)值計算所用到的質(zhì)量守恒方程和x，y，z方向的動量守恒方程如式(1)和式(2)所示：

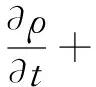
(1)

(2)

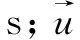
采用Standardk-ε模型進行湍流模擬，采用SIMPLE 算法進行壓力和速度耦合，二階迎風格式求解三維控制方程。風機集流器入口定義為速度入口，依次設置入口流速為15.44，16.70，17.88，19.08，20.28，21.46及22.67 m/s， 并分別定義為工況1～工況6。蝸殼出口定義為壓力出口，并將初始表壓設置為0，即沒有其他附加壓力作用。集流器及蝸殼采用無滑移固定壁面條件，風機葉輪定義為旋轉(zhuǎn)壁面。利用相對運動原理，旋轉(zhuǎn)葉輪和其他固定面的耦合采用多重參考系(MRF)模型。考慮到風機旋轉(zhuǎn)過程中風流的亞音速流動，即計算域內(nèi)的氣體不受體積壓縮和膨脹作用，故將空氣密度項設置為不可壓縮理想氣體模型。近壁面區(qū)采用標準壁面函數(shù)，重力和壁面粗糙度對流場的影響忽略不計。

高海拔地區(qū)環(huán)境溫度受季節(jié)、天氣等影響明顯，一天內(nèi)亦或呈現(xiàn)較大溫差，不易準確估算。但環(huán)境氣壓卻隨著海拔的升高呈現(xiàn)一定的規(guī)律降低，二者之間的關系被稱為“壓高方程”，根據(jù)高海拔大氣靜力學理論，在等溫假設的前提下，壓高方程如式(3)所示[13]：

(3)

式中：H為海拔高度，m；g為重力加速度，m/s2；T為大氣溫度，K；Rg為氣體常數(shù)；P0為平原環(huán)境大氣壓力，Pa；PH為海拔高度為H時的大氣壓力，Pa。

利用上述關系方程，將模型外界環(huán)境溫度統(tǒng)一設置為288.15 K(15 ℃)，則海拔高度與大氣壓力的關系如圖4所示。模擬時，對海拔高度分別為0，1 000，2 000，3 000，4 000和5 000 m條件下的離心風機流場及性能進行仿真計算。

圖4 海拔高度與大氣壓力關系曲線Fig.4 Relation curve between altitude and atmospheric pressure

1.4 實驗驗證

為驗證數(shù)值方法的可靠性，將常壓環(huán)境下的9-26-4A型離心風機性能參數(shù)模擬結(jié)果與該風機出廠性能曲線進行對比分析，如圖5所示。由圖5可知，軸功率與風量大致呈線性關系，全壓隨風量呈非線性減小趨勢。相同環(huán)境條件下，模擬風機軸功率和全壓結(jié)果與實驗結(jié)果整體趨勢保持一致，數(shù)值上的誤差也在可接受范圍內(nèi)。因此，本文采用數(shù)值模擬方法研究該離心風機性能是可行的。

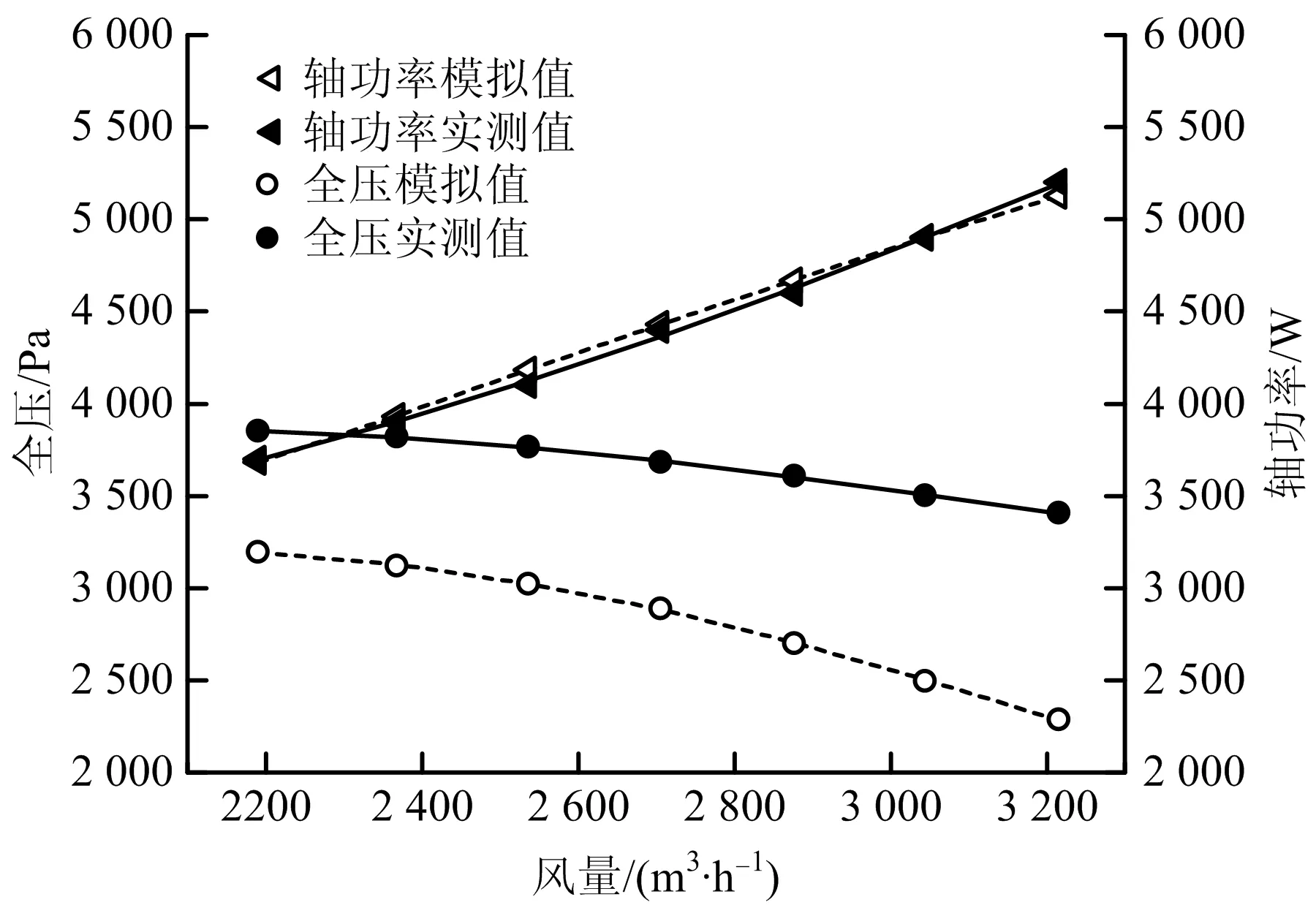
圖5 實驗驗證Fig.5 Test verification

2 數(shù)值模擬結(jié)果及分析

2.1 海拔高度對風機風壓的影響

為研究海拔高度對離心風機風壓大小的影響，選取工況4時的風機流場進行分析。圖6(a)～(f)分別為海拔為0，1 000，2 000，3 000，4 000及5 000 m高度時風機葉片附近全壓場情況。

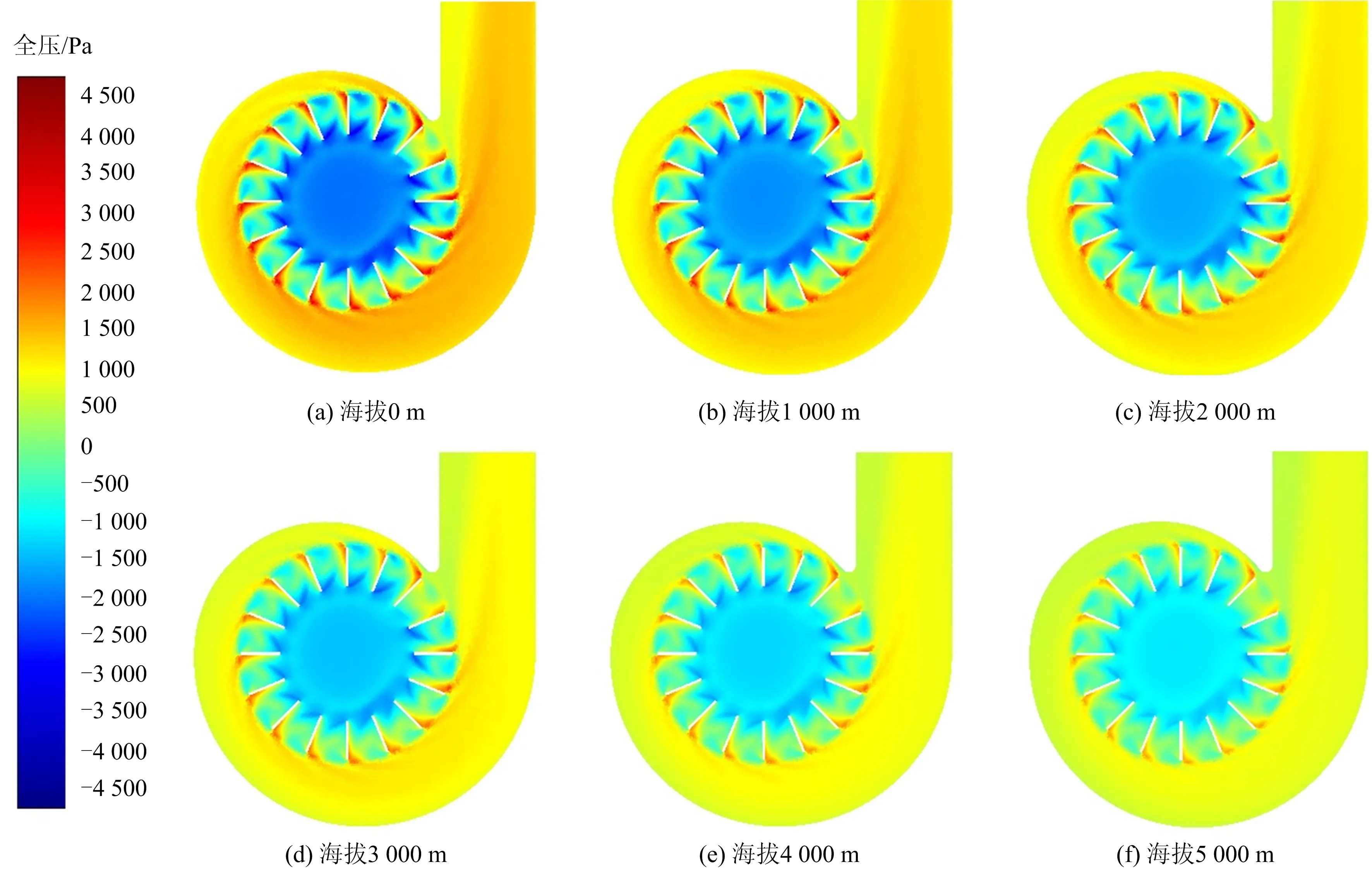
圖6 不同海拔高度條件下離心風機內(nèi)部全壓場Fig.6 Total pressure field inside centrifugal fan at different altitudes

由圖6可知，不同海拔高度時的風機內(nèi)部全壓場形態(tài)基本保持一致，即受蝸殼形狀影響，離心風機內(nèi)部壓力場呈現(xiàn)非對稱性，葉片外緣壓力高于內(nèi)緣壓力，且壓力面全壓值為正，吸力面全壓值為負。但隨著海拔的升高，葉片壓力面及吸力面全壓絕對值均減小，風機蝸殼出口全壓也呈現(xiàn)明顯減小趨勢。為直觀觀察離心風機輸出壓力與海拔高度的關系，計算不同工況條件下風機出口平均全壓與靜壓值，如圖7所示。

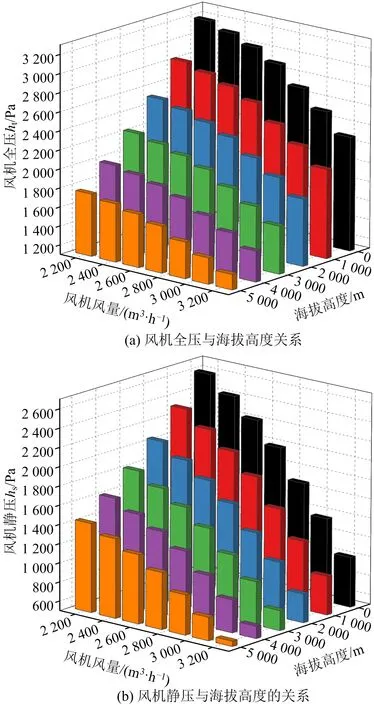
圖7 不同海拔及工況時的風機輸出壓力Fig.7 Fan output pressure at different altitudes and working conditions

由圖7可知，海拔高度不變時，風機全壓及靜壓均隨風量的增大而減小。相同工況風量條件下，隨著海拔的升高，風機輸出全壓及靜壓均呈顯著降低趨勢。為定量考察風機壓力與海拔高度的關系，對各工況時的二者關系曲線進行擬合分析，如圖8所示。由曲線及方程可知，風機全壓及靜壓隨海拔的升高均大致呈線性趨勢降低。經(jīng)計算，海拔每升高1 000 m，全壓降低9.3%左右，靜壓降低9.1%左右。

圖8 風機輸出壓力與海拔高度的關系擬合曲線Fig.8 Fitting curve of relationship between fan output pressure and altitude

2.2 海拔高度對風機功率的影響

軸功率和空氣功率是風機功率的2種類型，直接反映風機的功耗情況，風機軸功率Nfi和空氣功率Nfo可以分別利用式(4)，(5)計算：

(4)

Nfo=hf·Qf

(5)

式中：Nfi為風機軸功率,W；Nfo為風機空氣功率,W；π為圓周率，取3.14；Mf為風機葉片轉(zhuǎn)矩N·m；hf為風機輸出壓力,Pa；Qf為風機風量,m3/s。

根據(jù)數(shù)值模擬結(jié)果，統(tǒng)計不同海拔高度條件下的風機葉片轉(zhuǎn)矩值，見表2。由表2中數(shù)據(jù)可知，各工況條件下，隨著海拔的升高，風機葉片轉(zhuǎn)矩值逐漸減小，這說明輸出風量一定時，風機在高海拔地區(qū)葉片承受的載荷低于平原地區(qū)風機葉片載荷。將表2中風機轉(zhuǎn)矩數(shù)據(jù)帶入式(4)，可得到不同海拔高度條件下的風機軸功率大小，如圖9所示。由圖9可知，隨著工況風量的增大，風機軸功率值增大，但隨著海拔的不斷升高，軸功率呈顯著減小趨勢，即相同條件下，高海拔離心風機的功耗大大降低。圖10反映了風機軸功率與海拔高度的定量關系。由此可知，風機軸功率隨海拔的升高均大致呈線性趨勢降低。經(jīng)計算，海拔每升高1 000 m，軸功率降低9.0%左右。

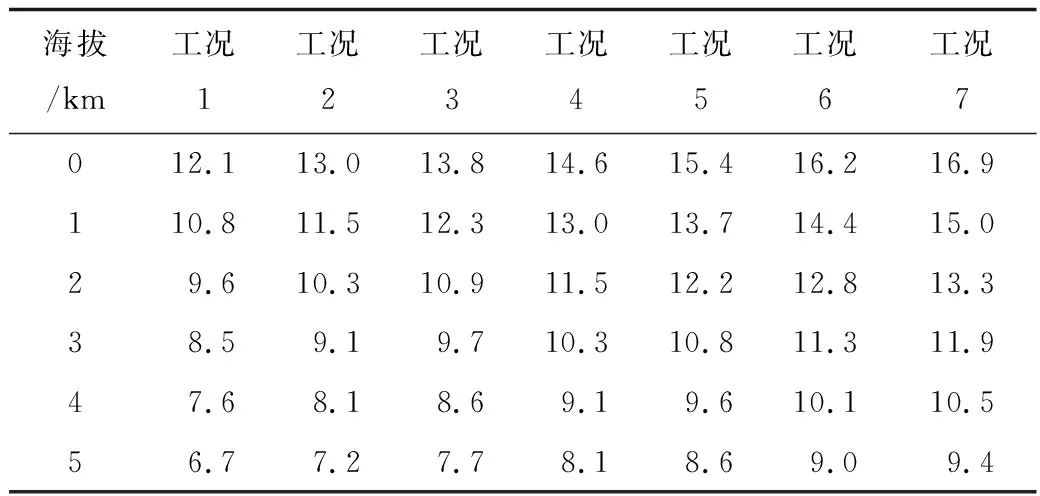
表2 不同海拔高度時的風機葉片轉(zhuǎn)矩Table 2 Torque of fan blade at different altitude N·m

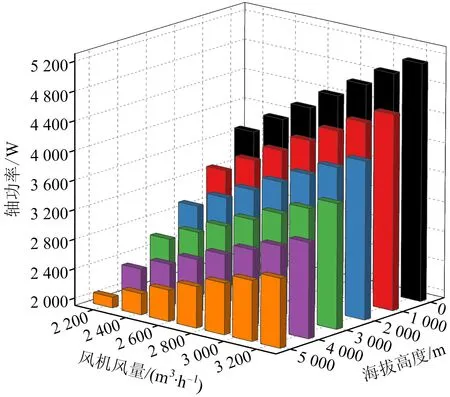
圖9 不同海拔及工況時的風機軸功率Fig.9 Axial power of fan at different altitude and working conditions

圖10 風機軸功率與海拔高度的關系擬合曲線Fig.10 Fitting curve of the relationship between fan shaft power and altitude

2.3 海拔高度對風機效率的影響

風流在通風機內(nèi)不僅有能量損失，而且還有機械磨損(在軸承上和油料箱中)和容積損失(風流在風機裝置內(nèi)的漏損)，風機裝置的空氣功率Nfo必小于軸功率Nfi，兩者的比值反映了風機的實際工作質(zhì)量，此比值稱為通風機的工作效率。

通風機的效率ηf計算如式(6)所示：

(6)

利用式(6)計算各海拔高度條件下的風機效率值，并繪制風機效率曲線，如圖11所示。由圖11可知，離心風機全壓及靜壓效率均隨風量的增大而呈非線性趨勢減小。而隨著海拔的升高，各工況條件下的效率值幾乎不受海拔高度的影響。為此，繪制風機效率與海拔高度的關系曲線，如圖12所示。由圖12可知，離心風機全壓及靜壓效率受海拔高度影響較小，經(jīng)計算，各工況條件下，海拔每升高1 000 m，風機全壓及靜壓效率分別平均降低0.21%和0.29%。

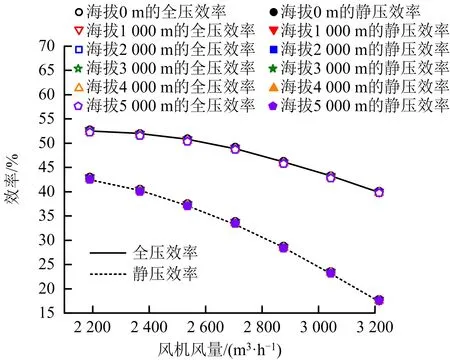
圖11 不同海拔高度條件下風機效率曲線Fig.11 Fan efficiency curve at different altitudes

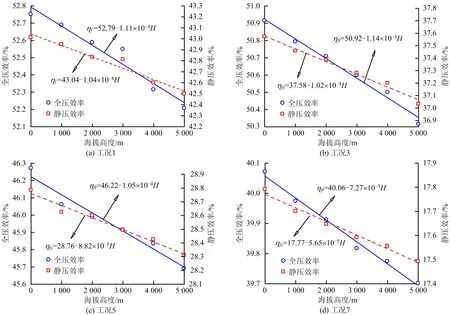
圖12 離心風機效率與海拔高度關系曲線Fig.12 Relation curve between centrifugal fan efficiency and altitude

3 結(jié)論

1)相同工況風量條件下，離心風機內(nèi)部流場形態(tài)不受海拔高度影響，但隨著海拔的升高，風機內(nèi)流場各處壓力絕對值均減小，風機蝸殼出口全壓及靜壓值呈線性降低趨勢，海拔每升高1 000 m，輸出全壓及靜壓分別降低9.3%及9.1%左右。

2)工況風量相同時，隨著海拔的升高，風機葉片轉(zhuǎn)矩減小，即風機葉片載荷減小，風機軸功率大致呈線性趨勢降低，海拔每升高1 000 m，軸功率降低9.0%左右。

3)離心風機效率受海拔高度影響較小，模擬結(jié)果表明，各工況條件下，海拔每升高1 000 m，風機全壓及靜壓效率分別平均降低0.21%和0.29%左右。