一種新型的樽海鞘群算法及其應用*
謝 聰,鄭洪清
(1.廣西大學行健文理學院,廣西 南寧 530005;2.廣西外國語學院信息工程學院,廣西 南寧 530222)
1 引言
近年來,隨著群智能算法的發展和應用,一系列新的算法被提出,如蜻蜓算法DA(Dragonfly Algorithm)[1]、水循環算法WCA(Water Cycle Algorithm)[2]、布谷鳥搜索CS(Cuckoo Search)算法[3]、灰狼優化GWO(Grey Wolf Optimizer)算法[4]、Jaya算法[5]和鯨魚優化算法WOA(Whale Optimization Algorithm)[6]等。2017年,Mirjalili等[7]提出樽海鞘群算法SSA(Salp Swarm Algorithm),它與其他群智能算法一樣存在后期收斂速度慢和易陷入局部最優等缺陷。一些學者對其進行了改進,文獻[8,9]通過Tent混沌序列生成初始種群并對最優個體采用精英質心拉伸機制,在食物源位置上引入瘋狂算子,并且在追隨者位置更新公式中引入自適應慣性權重來增強全局搜索能力;文獻[10]分別在領導者階段和跟隨者階段添加衰減因子和動態學習策略來提高算法的全局搜索能力;文獻[11]在領導者位置引入上一代樽海鞘群位置并加入了慣性權重策略,提高了算法的尋優精度和穩定性;文獻[12]將PSO(Particle Swarm Optimization)算法的隨機慣性權重引入SSA的追隨者位置更新公式中,其次用差分進化 DE(Differential Evolution)算法的變異操作替代SSA的領導者位置更新操作來提高收斂速度和計算精度;文獻[13]通過引入天體運動更新機制來提高算法的收斂速度和計算精度。上述算法雖然在一定程度上提高了算法性能,但仍有提升的空間。
針對以上問題,本文提出一種新型的樽海鞘群算法NSSA(a Novel Salp Swarm Algorithm),借鑒灰狼優化算法追隨α狼的思想,在SSA的追隨者位置更新公式中引入GWO算法的追隨機制,通過23個基準函數和2個圖像匹配問題對算法性能進行評測,驗證了NSSA的有效性。
2 樽海鞘群算法
樽海鞘群算法是Mirjalili等根據海洋中的樽海鞘的覓食行為而提出的一種群智能算法,其依靠領導者和追隨者的位置更新來完成問題優化。領導者的位置更新公式如式(1)所示:
(1)
c1=2e-(4*l/lmax)2
(2)
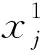
追隨者的位置更新利用式 (3)進行(牛頓運動定律):
(3)
其中,t是時間,a是加速度,v0是初始速度,a=(vfinal-v0)/t,v=(x-x0)/t,追隨者的位置更新公式如式(4)所示:
(4)
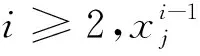
3 新型樽海鞘群算法
在基本樽海鞘群算法中,追隨者的新位置為當前追隨者與上一個追隨者位置的平均值,在迭代過程中形成鏈式結構,最終追隨至領導者位置,這一追隨方式是造成算法收斂速度慢和計算精度差的主要原因。針對基本樽海鞘群算法存在的不足,本文借鑒灰狼算法的ω狼追隨α狼的思想替換樽海鞘的追隨方式。因此,追隨者的位置更新公式如式(5)所示:
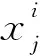
(5)
A1=2*a/r1-a
(6)
a=2-2*l/lmax
(7)
C1=2*r2
(8)
其中,r1,r2∈[0,1]為隨機數,其他符號含義與式(1)~式(3)相同。
新型樽海鞘群算法步驟如算法1所示:
算法1新型樽海鞘群算法
步驟1設置種群規模、初始迭代值、最大迭代次數和問題邊界等參數。
步驟2在邊界范圍內隨機初始化樽海鞘種群,求出領導者位置和相應值。
步驟3判斷是否達到最大迭代次數,如果是,輸出領導者和相應值,結束算法,否則進入步驟4。
步驟4首先執行式(2),然后對每一個樽海鞘執行式(1);再執行式(5)~式(8)。
步驟5對種群中每一個樽海鞘進行越界處理,求出領導者位置和相應值并判斷此時樽海鞘的值是否優于之前領導者值,如果是則用較優值替換較差值。
步驟6迭代次數加1,進入步驟3。
4 圖像匹配
基于灰度圖像匹配的數學描述:給定2幅灰度圖像S和T的大小分別為m1×n1和m2×n2,S和T分別表示原圖像和目標圖像,T(m,n)表示目標圖像上坐標(m,n)處的像素。令m2≤m1,n2≤n1,以S為原圖像,T為目標圖像,所求解的問題就是在S中搜索T的最優位置,采用歸一化積的最大相似度作為目標函數如式(9)所示:
(9)
其中,1≤i≤m1-m2+1,1≤j≤n1-n2+1。
算法2利用新型樽海鞘群算法求解圖像匹配
步驟1設置種群規模、初始迭代值、最大迭代次數和問題邊界等參數,導入圖像數據。
步驟2在邊界范圍內隨機初始化樽海鞘種群,利用式(9)求出領導者位置和相應值。
步驟3判斷是否達到最大迭代次數,如果是,輸出領導者和相應值,結束算法,否則進入步驟4。
步驟4首先執行式(2),然后對每一個樽海鞘執行式(1);再執行式(5)~式(8)。
步驟5對種群中每一個樽海鞘進行越界處理,利用式(9)求出領導者位置和相應值,并判斷此時樽海鞘的值是否優于之前領導者值,如果是則用較優值替換較差值。
步驟6迭代次數加1,進入步驟3。
5 仿真實驗與結果分析
為了驗證NSSA的性能和圖像匹配的效果,分別進行實驗1和實驗2。實驗1采用23個基準函數,并與其他算法進行性能比較;實驗2采用2個圖像匹配案例,并與其他算法進行性能比較。所有實驗均運行在處理器為Intel Celeron(R)雙核CPU T3200,2.90 GHz、內存為4 GB的Windows PC機上,以Matlab R2010a編寫代碼。
5.1 實驗1
用NSSA來求解全局優化問題,并與LECUSSA(LEvy flight-based Conditional Updating Salp Swarm Algorithm)[14]、SSA、WCA、CS、GWO和Jaya算法進行性能比較。所有算法的種群規模為30,最大迭代次數為500,23個基準函數如表1所示,其中Dim,Range和fmin分別表示維度、取值范圍和理論最小值;f1~f7為單峰值函數;f8~f23為多峰值函數。

Table 1 Benchmark functions
7種算法求解23個基準函數的結果如表2所示,每種算法獨立運行30次,結果均為30次實驗結果的平均值和標準差,加粗字體表示與其他算法比較時求解的最小值和標準差。從表2可知,對函數f6、f15和f20而言,NSSA求解的最優值比WCA、LECUSSA和CS算法求解的效果稍差。對其余20個函數中的5個函數:函數f14,NSSA求解效果與CS算法的一致;函數f16和f18,NSSA求解效果與LECUSSA、SSA、WCA和CS算法的一致;函數f17和f19,NSSA求解效果與SSA、WCA和CS算法的一致。對其他15個函數,NSSA求解效果均優于其他算法,尤其是對函數f3、f8、f9、f11、f21、f22和f23而言,NSSA求解的最優值均達到了理論最優值,而未達到理論最優值的結果也比其他算法的求解精度提高了幾到幾百個數量級。另外,從標準差可知,NSSA算法的魯棒性亦優于其他算法。
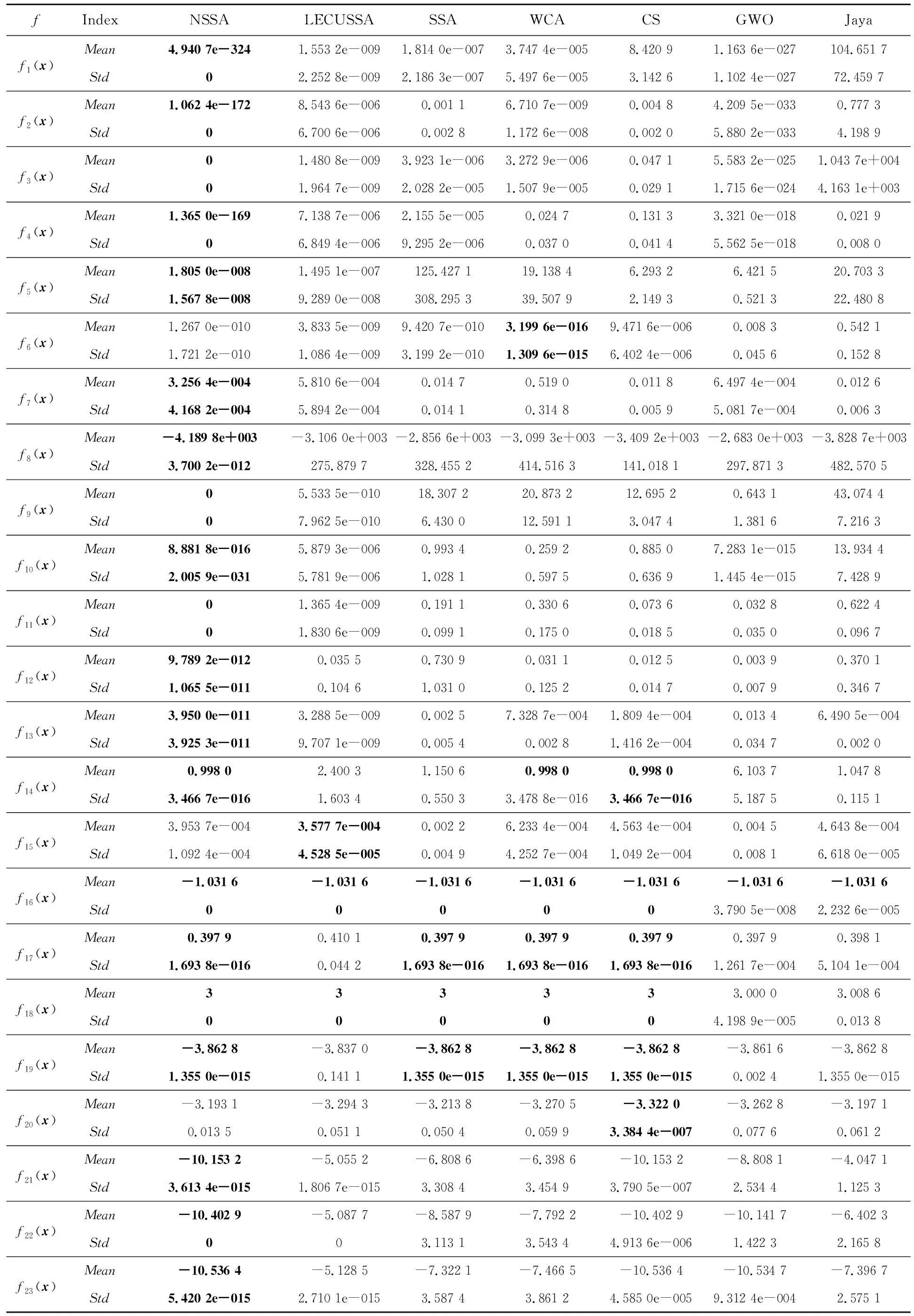
Table 2 Optimization results on benchmark functions
圖1~圖4給出了NSSA與其他6種算法在部分基準函數上的平均適應度曲線,從圖1和圖2可知,雖然NSSA初值收斂速度不是最快,但中后期進化明顯(由于線條重疊難以分辨,但從表1的函數值可知);從圖3~圖4可知,在初期和中后期NSSA收斂速度均為最快。
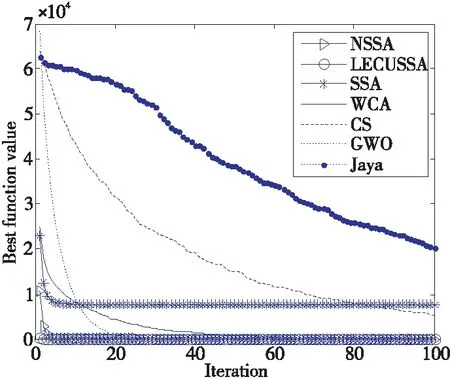
Figure 1 Average optimization curve on f1圖1 f1函數上的平均優化曲線
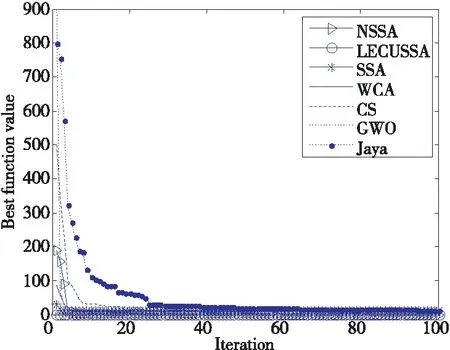
Figure 2 Average optimization curve on f2圖2 f2函數上的平均優化曲線
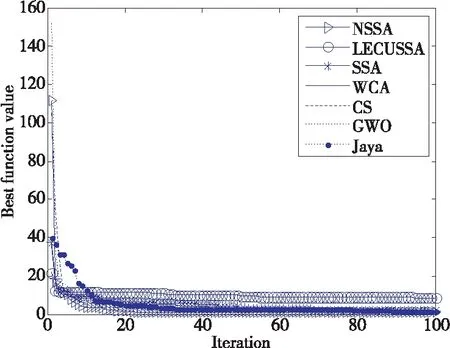
Figure 3 Average optimization curve on f14 圖3 f14函數上的平均優化曲線
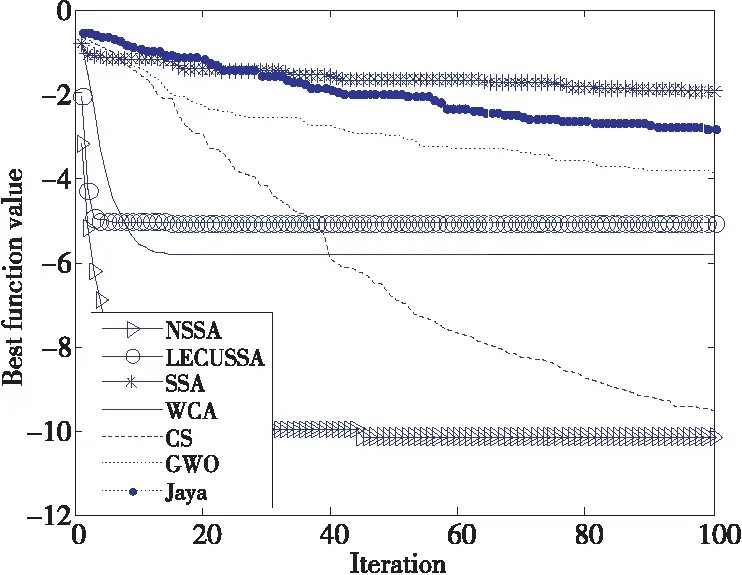
Figure 4 Average optimization curve on f21 圖4 f21函數上的平均優化曲線
5.2 實驗2
將NSSA應用于圖像匹配,并與其他4種算法進行比較,所有算法種群規模為30,最大迭代次數為100。
首先驗證NSSA在無噪聲環境中的有效性,以分辨率為512×512的Lena圖像為原圖像,取該圖坐標(220,220)為左上角,截取分辨率為100×100的子圖作為目標圖像,理想適應度值為1。
原圖像和目標圖像分別如圖5a和圖5b所示,利用NSSA進行圖像匹配的結果如圖5c所示,圖中的黑色框線表示匹配到的實驗結果。

Figure 5 Result of matching Lena image with NSSA 圖5 NSSA匹配Lena圖像的結果
為了展示NSSA的有效性,將其迭代次數與平均適應度值關系的仿真結果與其他算法比較,如圖6所示。由圖6可知,NSSA在30次迭代過程中,大約在30代左右達到理論最優值1,而此時其他算法平均適應度值均未達到最優。另外,30次實驗的平均運行時間(平均運行時間為達到理論值1所需時間,即為匹配成功的時間)及匹配率如表3所示。由表3可知,本文NSSA的平均運行時間僅為0.093 s,匹配率為100%,可見NSSA的匹配速度和匹配精度遠優于其他算法。
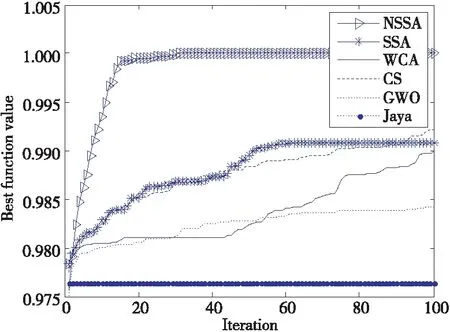
Figure 6 Comparison of average convergence curve of 6 algorithms圖6 6種算法平均收斂曲線比較
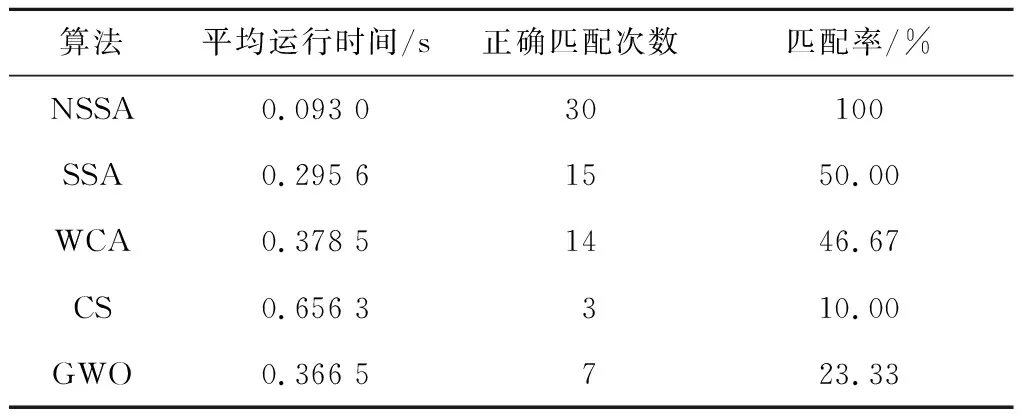
Table 3 Comparison results of each algorithm on Lena
再驗證NSSA在有噪聲環境中的有效性,選取分辨率為512×512的Couple圖像進行測試,取該圖坐標(123,131)為左上角,截取分辨率為100×100的子圖作為目標圖像,理想適應度值為1。給原圖像和目標圖像添加均值為0、方差為0.05的高斯噪聲,分別如圖7a和圖7b所示,利用NSSA進行圖像匹配的結果如圖7c所示,圖中的黑色框線表示匹配到的實驗結果。另外,30次實驗的平均運行時間(平均運行時間為達到最大迭代次數所需時間,因為此時無法達到理論最優值1)及匹配率如表4所示。由表4可知,在高斯噪聲下的Couple圖像,NSSA的匹配成功率依然最高,為93.33%,且耗時在0.45 s左右。雖然所有的算法都能成功匹配,但目標函數值均不能達到理論最優值1。綜上所述,所有的實驗均表明了NSSA具有更好的收斂速度、匹配精度和魯棒性。

Figure 7 Result of matching Couple image with NSSA 圖7 NSSA匹配Couple上圖像的結果
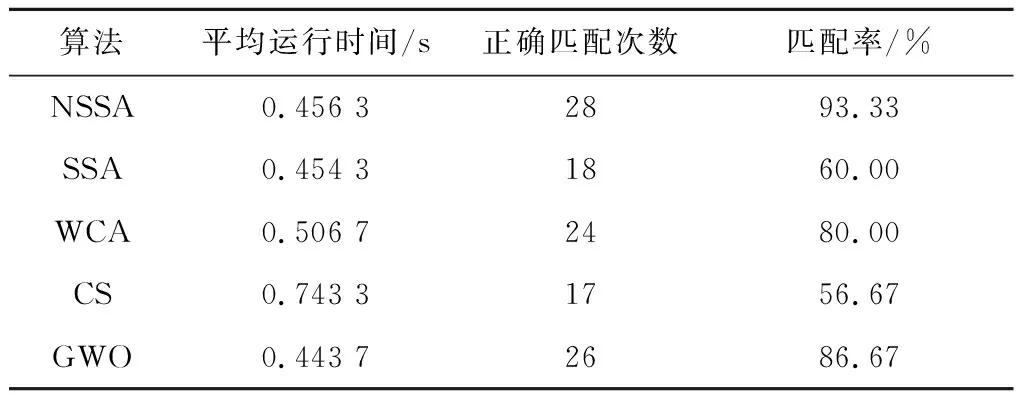
Table 4 Comparison results of each algorithm on Couple
6 結束語
本文針對基本樽海鞘群算法在后期收斂速度慢和易陷入局部最優等缺陷,分析了樽海鞘的追隨領導者方式是造成其缺陷的主要原因,借鑒灰狼優化算法中ω狼追隨頭狼的思想替換樽海鞘追隨領導者的方式,提出一種新型的樽海鞘群算法NSSA。通過23個基準函數和無噪聲及有噪聲圖像匹配的仿真實驗表明,所提算法具有更好的收斂速度、計算精度和魯棒性。

