基于MRF模型的飛機飛行動作識別劃分算法*

顏廷龍，李 瑛，王鳳芹

(1.海軍航空大學岸防兵學院，山東 煙臺 264001;2.海軍航空大學航空基礎學院，山東 煙臺 264001)

1 引言

飛行動作的識別和劃分一直是飛機健康監控、飛行模擬和飛行品質評估等應用的基礎，快速準確地識別飛機的基本飛行動作和復雜飛行動作具有重要意義。由于民航飛機動作更加平穩，識別劃分難度小，相關的研究已經比較成熟，而軍用戰機由于其機動性強、速度快的特點，其飛行動作識別一直以來都是難點問題。

目前，飛機動作識別劃分主要分為以下幾種方法：一是根據專家的先驗知識，預先設定規則，建立知識庫識別飛機的機動動作。倪世宏等[1]分析了軍用飛機的飛行動作的變化特征，建立了基于專家先驗知識和飛行動作特征的知識庫來識別飛機的飛行動作，但這種方法的缺點在于面對不同的飛機型號，設置的規則不具有通用性，另外，專家的先驗知識可能帶有主觀誤差。二是利用目前的機器學習算法，比如貝葉斯網絡、支持向量機和神經網絡監督學習算法等。沈一超等[2]基于時間序列的DTW(Dynamic Time Warping)距離和貝葉斯網絡推理，提出了一種基于貝葉斯網絡的飛行動作識別算法，可以識別復雜飛機動作。這些方法要求預先將帶有基本飛行動作標記的飛行時間片段作為訓練集[3 - 6]，訓練一個分類器，區分不同飛行數據，要求事先人工標記訓練集，工作量較大，而且模型的通用性不強。

馬爾可夫隨機場MRF(Markov Random Field)[7]模型是概率圖模型的一種，它可以表示時間序列中相鄰2個隨機變量的相關關系，在飛行數據的時間序列中，可反映相鄰時間點的參數的相關性。比如，飛機在t時刻的操縱參數，會影響t+1時刻的姿態參數。因此，本文在飛行動作識別領域，引入馬爾可夫隨機場模型，提出了一種基于馬爾可夫隨機場模型的飛機飛行動作識別劃分算法，采用基于馬爾可夫隨機場的時序數據分割聚類算法，將飛行數據序列劃分為多個動作類，并且用MRF網絡描述其每個動作的特征。

2 飛行動作識別劃分模型

2.1 馬爾可夫隨機場模型

馬爾可夫隨機場MRF是在隨機場的基礎上添加馬爾可夫性質，使得隨機序列變量的分布僅與前一時刻有關。這一性質提供了方便且具有一致性的建模方法，可以用來表示時間序列前后的約束關系。一維的馬爾可夫隨機場描述隨機序列中某一時刻的狀態只與前一時刻有關，二維的馬爾可夫隨機場常常被用在圖像分割領域，將時域的馬爾可夫特性轉換到空間域，每個像元對于除它之外的相鄰的像元組成的鄰近集團存在依賴性，通過這一性質，進而有效地描述圖像的局部統計特征。在多維時間序列上定義MRF網絡，將多維時間序列描述為一個由隨機變量組成的多層網絡，相鄰層的網絡通過網絡節點的邊相連，網絡各個節點之間的邊描述各個變量之間的相關關系。區別于傳統飛行動作分類方法依賴于飛行數據序列距離的度量[8]，本文算法應用MRF的特性，用MRF網絡表示飛行數據序列前后的依賴關系，從而得到更精確的飛行動作分類結果。

2.2 飛行數據時間序列分析

飛行數據是一組離散的時間序列數據，飛行動作識別的準確程度，很大程度取決于各個飛行動作的劃分結果，本文提出基于馬爾可夫隨機場的時間序列分割算法，對飛行數據進行分割和聚類，以完成對飛行動作的劃分。設飛機的一組長度為T的飛行數據為x=[x1,x2,x3,…,xT],其中xi(i≤i≤T)為n維向量，表示同一時刻采集的n維飛行數據。設需要將待劃分的飛行數據分為K類，針對時間序列的聚類方式，不能僅對單獨數據點聚類，還要根據數據前后的相關變化規律進行聚類，因此通過設置一個滑動窗口w，其中w?T，w數值的選取取決于飛行數據的粒度和預期飛行動作的長度。以t時刻為基準，向前截取窗口大小的數據片段，記為Xt：

Xt=[xt-w+1,…,xt-1,xt]

其中,t=1,2,…,T,Xt為n×w維向量，將原始飛行數據截取長度為w的多個子序列，將此時針對飛行數據的聚類變為對長度為w的多個子序列的聚類，這樣在聚類過程中，相鄰的子序列更易被劃分為同一類，實現時間一致性的目標。

設需要將待劃分的飛行數據分為K類，屬于第j類的數據段集合記為Pj,其中j=1,2,…,K。每個類用高斯協方差矩陣定義，類的協方差逆矩陣Θj反映各個參數之間的獨立性。Θj是一個nw×nw矩陣，由w×w個子矩陣組成，每個子矩陣是大小為n×n的矩陣，位置pq上的子矩陣描述p時刻和q時刻之間，n個維度之間的協方差逆矩陣。由于飛行數據是非時變的，即每一個點的參數值只與相應時間差有關。

2.3 基于MRF模型的飛行動作識別劃分算法

MRF模型需要根據統計決策和估計理論中的最優準則確定時間序列分割問題的目標函數，采用一些優化算法可求得滿足這些約束條件的MRF最大似然分布[9]。本文采用多元飛行數據時間序列各個維度之間的協方差逆矩陣Θj定義了MRF網絡的鄰接矩陣，通過估計稀疏的高斯逆協方差矩陣來學習每個聚類的MRF，MRF網絡具有多個層，層數對應于定義的短子序列的窗口大小，通過求解帶約束的逆協方差逆矩陣估計問題，即可解決飛行動作的分類問題。那么，針對飛行數據時間序列進行劃分和識別變為求解每類飛行動作的參數之間的協方差逆矩陣Θ={Θ1,Θ2,…,ΘK}和每類飛行動作的數據段集合P={P1,P2,…,PK}。

用負對數似然函數表示飛行數據段Xt被歸為基本動作j類的代價，如式(1)所示：

E(Xt∈Pj)=-ll(Xt,Θi)=

(1)

其中，ll(Xt,Θi) 表示對數似然函數,μi表示矩陣Θi的均值，detΘi表示矩陣Θi的行列式。

考慮飛行數據的連續性，相鄰時刻的數據段屬于不同類時施加懲罰項β，β越大，相鄰的飛行數據子序列被劃分為同一類動作的可能性越大。當β=0時，飛行數據子序列可以被單獨劃分，連續性懲罰項表達式如式(2)所示：

(2)

由于極大似然估計不能產生稀疏解，導致模型的復雜度過高，不方便求解，需要加入稀疏性約束，增加正則化懲罰項，如式(3)所示：

λ‖Θi‖

(3)

其中,λ是正則化參數。稀疏化可以極大地簡化網絡結構，一定程度上降低了本文算法的復雜性，還可以提高模型的泛化能力，解決模型的過擬合問題。

綜上所述，模型的總體優化函數如式(4)所示：

(4)

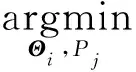
3 飛行動作識別劃分模型的求解方法

MRF模型的總體優化函數求解是一個組合和連續優化問題，飛行動作劃分參數的求解和飛行動作類參數協方差逆矩陣的求解互相耦合，是高度非凸的優化問題。解決這一問題的關鍵在于采用期望最大化EM(Expectation Maximum)算法將總體優化目標轉化為飛行動作識別和飛行動作劃分2個子問題，交替更新參數，迭代求解，其中飛行動作劃分參數使用動態規劃算法求解，飛行動作識別參數采用交替方向乘子法ADMM(Alternating Direction Method of Multipliers)求解[10]。

3.1 飛行動作劃分的參數求解

針對飛行動作劃分的參數Pj的求解問題，首先要給定Θj，此時Pj的優化要考慮2個方面的問題，一是飛行數據段Xi被歸為j類的代價，可以用負對數似然函數和表示，即式(1)，另一個是飛行數據的連續性約束，應用式(3)表示。2個代價構成典型的流水線問題，可以采用動態規劃算法進行求解[11]。

動態規劃算法將T個子序列X1,…,XT分配到K個聚類的問題，等效為找到時間戳1～T的最小代價路徑，其中節點代價是將該數據段分配給飛行動作的負對數似然函數和，并且每當分類改變時，邊的代價為β。

3.2 飛行動作識別參數矩陣的求解

首先要給定一類中所有數據段的集合Pj，通過求最小化負對數似然總和，可以求解Θi，如式(5)所示:

E1+E2

(5)

其中,E1=-|Pj|log det(Θi)，E2可以寫成跡的形式，如式(6)所示：

(6)

其中，Si是經驗協方差，由當前Pj所有數據段計算得到。考慮矩陣的稀疏性，添加一個正則項λ‖Θi‖，所以逆協方差逆矩陣的優化函數如式(7)所示：

(7)

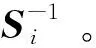
本文采用ADMM算法，ADMM是一種分布式凸優化算法，主要應用在大規模優化任務中[12]。為了使問題更符合ADMM算法的形式，引入變量Z并將原問題重寫為等效問題，如式(8)所示。

min(-log detΘ)+tr(SiΘ)+‖λ·Z‖1

subject toΘ=Z,Z∈Γ

(8)

其增廣拉格朗日函數為：

Lp(Θ,Z,U)=-log detΘ+tr(SiΘ)+

(9)

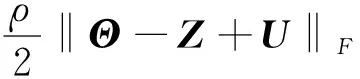
(10)

(11)

Uk+1:=Uk+Θk+1-Zk+1

(12)

其中k是迭代參數。

3.3 EM算法求解整體優化問題

本文利用迭代EM算法[13]解決數據段分類和聚類參數協方差逆矩陣的問題。隨機初始化集群，并且交替執行E-step和M-step，直到每個簇的分配已經固定，模型已經收斂。本文算法的求解步驟如下所示：

步驟1初始化模型參數Pj，Θi；

步驟2執行E-step，給定Θi，應用動態規劃算法將飛行數據分到各個飛行動作類，求解Pj；

步驟3執行M-step，給定Pj，應用ADMM算法更新飛行動作識別參數Θi；

步驟4重復執行步驟2和步驟3，不斷地迭代直到算法收斂。

4 實驗與結果分析

4.1 實驗方法

為了方便驗證本文算法的準確性，采用海軍某型飛機的50次飛行任務記錄的飛行數據進行實驗，每次飛行任務的時長大約為1 h，將每次飛行任務的數據劃分為10組，共500組。選取其中與飛行動作識別相關的發動機轉速、飛行速度、飛行高度、航向角、俯仰角和傾斜角6個參數。為了驗證實驗結果，飛行數據已經事先采用人工標記各個階段所屬的基本飛行動作，飛行數據的采樣間隔均為1 s，算法的參數設置為：滑動窗口大小w設置為5，根據飛行基本動作的種類，將聚類簇的個數K設置為5。

4.2 識別率對比

由于飛機機動平飛的過程占很大一部分，所以單純使用識別率不足以來評價算法的識別效果，本文使用Macro-F1 值評價各個算法的識別準確率。Macro-F1值計算方式是先計算每一個類的Precison和Recall后，再計算各個類的F1值，然后將各個類的F1值的平均值，其中：

(13)

表1是本文算法(記為MRF)、基于高斯混和模型的聚類算法(記為GMM)[14]，基于歐氏距離的DTW算法(記為DTW)[15]、基于自組織圖的人工神經網絡聚類方法(記為Neural Gas)[16]和k-means算法針對測試樣本聚類的Macro-F1值和部分動作識別準確率。

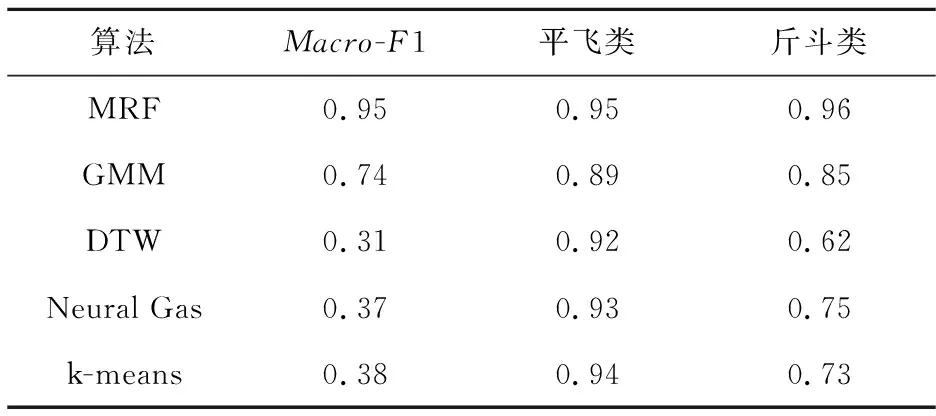
Table 1 Comparison of Macro-F1 values of various algorithms

從表1可以看出，雖然5種算法對平飛的識別準確率都很高，但DTW、k-means、Neural Gas對于斤斗類動作的識別準確率較低。斤斗類的飛行數據變化比較復雜，而這些算法大多使用基于距離的判定規則，無法識別飛行數據表示的本來特征。所以，本文算法在復雜動作的表現上優于其他基于距離的算法。

接下來測試各個算法需要多少樣本才能準確聚類，識別飛機動作。圖1所示為5種算法的Macro-F1值與樣本數量的關系圖。如圖1所示，本文算法的性能明顯優于其他算法，Macro-F1的值為0.91～0.98。與其他基于距離的聚類算法相比，本文算法只需更少的樣本就能達到相似的準確率，而基于距離的聚類算法的結果準確率不高，難以對飛機動作進行劃分。

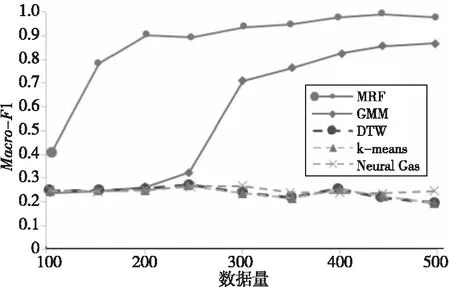
Figure 1 Relationship between Macro-F1 value and data volume圖1 Macro-F1值和數據量關系

當有100個樣本時，沒有一種算法能夠準確地識別飛機的動作。但是，隨著樣本量的增多，基于本文算法的準確率迅速提高。當有200個樣本時，本文算法的Macro-F1已經超過0.9。

4.3 模型參數分析

(1)時間一致性參數。

圖2所示為本文所提算法和去除算法中時間一致性約束MRF(β=0)的Marco-F1值和數據量之間的關系。由圖2可知，由β定義的時間一致性約束在數據量較小時僅具有很小的影響，因為MRF和MRF(β=0)都獲得了相似的結果。但是，隨著樣本數量的增加，MRF(β=0時)的Marco-F1徘徊在0.9附近。這意味著，一旦有足夠的樣本，飛行數據連續性約束這一參數的設置是提高算法性能的決定性因素。

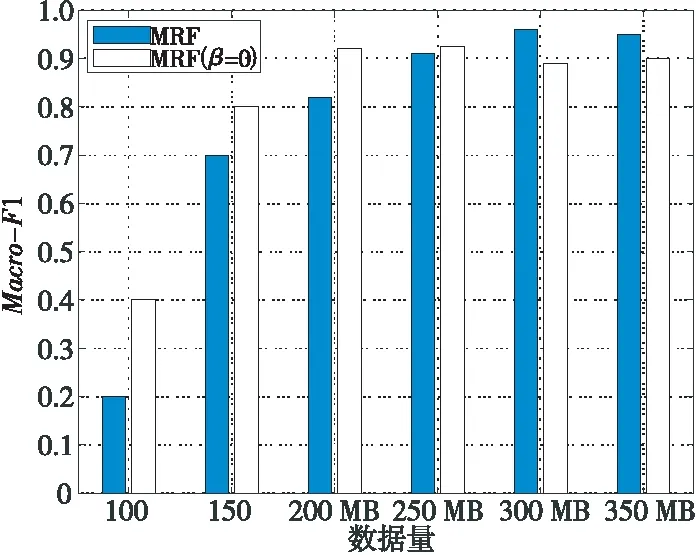
Figure 2 Influence of time consistency parameter 圖2 時間一致性參數影響

(2)滑動窗口大小分析。

圖3所示為本文算法中滑動窗口大小和Marco-F1值之間的關系，可以觀察到算法滑動窗口大小設置為4～15可得到較高Marco-F1聚類準確率評分。只有在窗口大小降至4以下或升至10以上時，算法準確率較低。

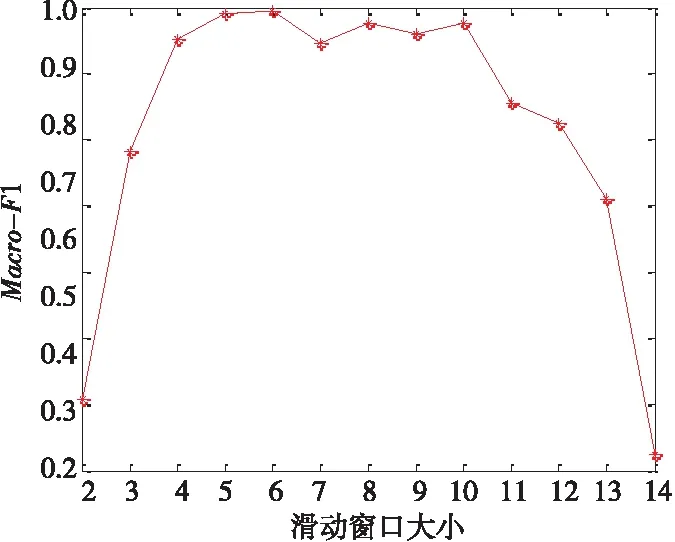
Figure 3 Influence of sliding window size 圖3 滑動窗口大小影響

5 結束語

本文研究了基于MRF模型的飛機飛行動作劃分和識別算法，算法在對飛行動作準確識別和劃分的同時，還提供了結果的可解釋性。通過對比其他算法的Macro-F1值表明，本文算法提高了飛行動作識別的準確率。