林用無人機航跡非概率不確定性優化
徐玉潔 鄭哲文
(中南林業科技大學材料與工程學院,湖南 長沙 410004)
引言
我國森林資源分布不均勻,森林的占有面積僅為世界的1/6,存在問題有很多。森林火災是森林災害中破壞性最強的,也是林業中最為可怕的災害。森林防火是森林保護的重要內容。如何做到有效防火是人們日益關心的問題[1]。無人機具有成本較低、機動速度快、維修簡單等特點,用途廣泛;但無人機在環境未知的空間中飛行,會面臨大量動態、未知的限制因素,如噪聲、氣流影響、傳感器限制等[2],這些因素的變化會導致在建模過程中的結構參數不確定。傳統的優化模型均解決確定性問題,環境較為理想化,然而實際環境會受諸多因素影響。林用無人機受動態環境因素影響不確定性因素較多,如天氣、風速以及無人機性能本身等,需要考慮實際工程結構中的不確定性以及對應的優化方法。不確定性的度量通常有概率與非概率模型,概率型所需樣本較多,雖然計算較為精確,但成本較高,在實際情況下適用度不高;非概率模型所需樣本相對較少,只需確定邊界即可,雖然不確定性因素的詳細信息很難獲取或者根本無法知道,但是其不確定性的邊界往往是很容易確定的[3]。人們對區間模型的理論和應用進行了廣泛研究[4-8]。在求解區間模型的方法中,J Wu等[9]提出在不確定區間結構下基于區間算法和切比雪夫區間擴張函數的魯棒拓撲優化方法;Jiang C等[10]基于區間序關系將不確定的目標函數和約束轉化為確定性的模型,然后采用改進的帶懲罰函數的遺傳算法進行求解;姜潮[11]提出非線性區間數優化的數學轉換模型即確定和不確定性之間的相互轉換模型;符純明[12]提出基于IDE模型不需轉換直接求解不確定優化問題;邱志平和祁武超[13]提出結構非概率可靠性優化模型等。本文采用了符純明[12]基于區間差分進化算法來解決非線性區間優化問題,該算法可直接求解無需轉換,在方法上更為簡便,計算效率較高,保真度較好。
1 區間不確定性優化
過去由于研究條件和手段的限制,通常把實際問題簡化為理想化模型予以考慮,然而實際中存在大量的不確定因素。隨著社會進步和科技發展,不確定性所帶來的后果越來越受到人們的重視。無人機所處工作環境中的不確定因素非常顯著,如果繼續予以確定性問題來研究,難免會產生意想不到的后果,所以對無人機進行不確定分析很有必要。不確定性的度量通常有概率和非概率2種模型,概率模型所需樣本多,雖在算法上有較強的數學依據,但是其抽樣成本較高,適用度不適合少樣本及成本高的場合。而非概率模型中的區間模型[14]只需要確定上下界,不需要具體的概率分布,具有成本低、適用度廣等優點,越來越受到人們的青睞。
1.1 區間
根據區間數學[15],區間數的定義是一組有序的實數:
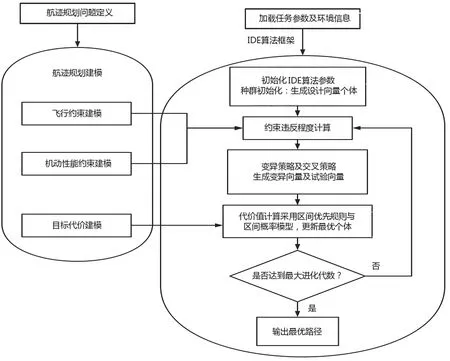
AI=[AL,AR]=[x|AL (1) 式中,I、L、R分別表示區間、區間下界和區間上界,當L=R時,區間為一實數。 區間也可以用中點和半徑表示: AI=〈AC,AW〉={x|AC-AW (2) 式中,AC是中點;AW是半徑。 (3) (4) 普通的參數為固定值,參數用區間表示就不為某一實數,而是區間數,是一個服從更均勻分布的波動。 大多數求解非線性區間優化的方法是將原始不確定性問題轉換成確定性問題,求解過程復雜,計算量大,結果誤差較大,求解問題僅限于最一般的不確定性問題,局限性較大。而直接法不需進行轉換,在一般的計算資源中均可使用,為了避免將不確定性優化問題轉化為確定性問題,本文采用符純明的基于區間差分進化算法來解決非線性區間優化問題,其中區間概率模型用于確定不確定性優化問題的區間約束[12],區間優先規則用于選擇當前最優的解決方案以保留到下一個進化種群中。區間差分進化算法主要包括4個步驟,初始化、變異、交叉和選擇策略。 1.2.1 初始化 (5) 式中,i=1,2,…,NP;j=1,2,…,N;randj(0,1)是一個在區間(0,1)上服從均勻分布的隨機數。 1.2.2 變異策略 第g次迭代時,差分變異操作產生變異向量。常見的差分變異算子: DE/rand/1/bin Vi,k=Xr1,k+F(Xr2,k-Xr3,k) (6) DE/rand-to-best/1/bin Vi,k=Xr1,k+F(Xbest,k-Xr1,k)+F(Xr2,k-Xr3,k) (7) DE/rand/2/bin Vi,k=Xr1,k+F(Xr2,k-Xr3,k)+F(Xr4,k-Xr5,k) (8) DE/current-to-rand/1/bin Vi,k=Xi,k+F(Xr1,k-Xi,k)+F(Xr2,k-Xr3,k) (9) 式中,r1,r2,r3,r4,r5∈{1,2,…,NP}均為兩兩互不相同的整數,且與當前的目標向量索引i不同,因此要求種群規模NP≥4;F為縮放因子,是介于(0,1)的常數,用于控制差分向量的大小。F過小會降低收斂速度,但F也不能過大,否則種群將無法收斂。 1.2.3 交叉策略 在變異操作后,需要將目標向量Xi,k與變異向量Vi,k進行二項式交叉,生成最終的試驗向量Ui,k=[ui,1,k,ui,2,k,…,ui,N,k],按照以下公式執行交叉操作。 (10) 式中,jrand是從集合{1,2,…,N}內隨機選取的一個整數,以保證變異向量Vi,k至少有一維信息被保留下來。交叉概率CR是(0,1)區間范圍內的一個常數。 1.2.4 選擇策略 傳統選擇策略對試驗向量ui,k與目標向量Xi,k的目標函數值進行比較,若ui,k具有更優的目標函數,則將Xi,k替換為ui,k;否則,Xi,k保持不變。以目標最小化為例,選擇操作可表示為: (11) 而區間優先規則在原有選擇策略的基礎上引入區間概率模型,主要用于量化評估一個區間優于或劣于另一個區間。對于區間Al和Bl,區間概率: (12) 則第j個不等式對應的區間概率: (13) 通常情況下,無人機航跡規劃是指在任務區域D={(xi,yi,zi)|i∈(1,n)}內,在滿足飛行約束和機動性能約束的前提下,計算獲得一組最優路徑規劃點pi=(xi,yi,zi),最終使整個規劃代價最小,其優化問題可描述為: (14) 飛行約束條件包括以下幾點。 轉向角約束:為了保證飛行軌跡平滑,在每一航路點的最大轉向角[16]可表示: (15) 式中,nmax為最大橫向過載;g為重力加速度;V為飛行速度;則無人機轉向角約束為: φ1=max(μi-μmax)≤0 (16) 爬升/下降約束:路徑點pi處的斜率si由最大爬升斜率βi和最小下降斜率γi約束[17],可表示: (17) (18) 爬升和下降約束: (19) 在實際優化問題建模時,優化問題的目標函數和約束函數中往往含有不確定變量及參數,引入區間模型后,原問題的形式轉化: (20) (21) (22) (23) (24) (25) (26) 無人機航跡規劃流程如圖1所示。 圖1 林用無人機航跡規劃流程圖 無人機航跡規劃的過程中,其環境信息往往是動態的、不確定的,在實際場景下已知的信息會發生一些變化,如產生運動障礙(飛鳥、空中散落的樹枝)或者地圖信息改變(植被生長更替)等,因此需要對動態環境進行算法驗證。為了驗證本文所述區間差分進化算法的有效性,對無人機森林航跡規劃的3個地圖的20組實驗結果進行分析與討論。設置任務區D=[0,1500]×[0,1500]×[0,2500],m;算法初始參數配置為NP=200,kmax=500,F=0.8,CR=0.2,α=0.3;第2部分的具體飛行參數及不確定參數區間見表1。 表1 飛行參數及不確定區間 本文同時給出基于區間差分進化算法IDE的路徑規劃、傳統的非區間優化算法(遺傳算法[18]GA、差分進化算法DE)的路徑規劃以及IP-GA結果,如表2所示。相比傳統的非區間優化算法(GA、DE),區間差分進化算法生成的路徑長度與代價值更小,對比GA,最優子路徑縮短了約18.26%。與基于區間的非線性優化方法IP-GA相比,IDE在路徑長度更長的地圖中具備更大優勢。通過對比GA、DE、IP-GA、IDE算法的收斂性,由圖2可以看出,區間差分進化算法和IP-GA收斂性較強,但IDE算法運行時間至少比IP-GA算法快了10.39%。綜合多次搜索路徑結果來看,區間差分進化算法搜索結果更穩定,魯棒性更強。綜合比較表中數據,區間差分進化算法在不確定性空間下的全局路徑規劃能力表現出良好的性能。 表2 3個地圖中不同算法的路徑長度、代價值和運行時間的統計結果 圖2 對比GA、DE、IP-GA、IDE算法的收斂曲線 本文對考慮不確定性參數的非概率林用無人機航跡規劃問題進行研究,通過描述不確定性參數對無人機航跡規劃進行建模,采用一種基于區間差分進化算法的非線性不確定優化問題的分解分析方法,選擇最優的解決方案來提高算法搜索效率。研究表明,采用區間差分進化算法的林用無人機航跡優化可直接處理存在于目標函數和約束中的區間不確定性,無需進行轉化,適用度高,結果保真度較好;基于區間差分進化算法的林用無人機航跡規劃能夠有效考慮不確定參數對最優路徑的影響,其優化效率較高;相比于GA、DE、IP-GA算法,基于區間差分進化算法擁有更好的魯棒性,平均搜索路徑更短,對比IP-GA求解效率提升約10.39%。1.2 區間差分進化算法
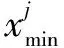

2 無人機航跡規劃建模
2.1 無人機航跡規劃確定性模型
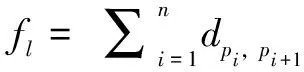
2.2 無人機航跡規劃不確定性模型
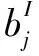
3 算例分析



4 結論

