基于多路徑Radon變換的地震數據噪聲壓制和波型分離方法研究

唐歡歡，毛偉建*

1 中國科學院精密測量科學與技術創新研究院計算與勘探地球物理研究中心，武漢 430077 2 大地測量與地球動力學國家重點實驗室,武漢 430077

0 引言

抗噪性能良好的Radon變換被廣泛應用于圖像分析和信號重構等方面，它是一種積分變換，在地震勘探數據處理領域，根據積分路徑的不同，Radon變換可分為線型、雙曲型以及拋物型(Thorson,1978;Hampson,1986;Yilmaz,1989).線性Radon變換(Linear Radon,L_Radon)又稱為傾斜疊加，它是將時空域的同相軸振幅沿著偏移距方向以一定的斜率進行疊加運算，因此線性同相軸在線性Radon變換域的系數表現為一個強能量點，對應的縱橫坐標分別表示同相軸的時間截距及速度信息；而隨機噪聲經過線性疊加后在變換域分布無規律且能量極弱，該特征有利于隨機噪聲壓制(Turner,1990;鞏向博等，2009；Sabbione et al.,2015)、面波壓制(李衛忠等，1998；Wang,1999;張智等，2017)以及波場分離(Moon et al.,1986;王維紅等，2006；李志娜等，2014；Lin and Sacchi,2020).但在油氣勘探地震數據中，有效信號為反射波，其時距曲線為雙曲型，經過線性Radon變換后，其變換系數分布并不集中，失去了變換的稀疏性特征且物理意義不明顯.Hampson(1987)將雙曲Radon變換(Hyperbolic Radon,H_Radon)引入到地震數據重建中，但雙曲Radon變換在頻率域不解耦，只能在時間域進行計算導致效率較低(Spitzer et al.,2001;石穎和王維紅，2012).雙曲型同相軸經過部分動校正后可近似為拋物型，而拋物Radon變換(Parabolic Radon,P_Radon)在頻率域是解耦的，且在頻率域具有共軛對稱性使其計算效率較高，因此拋物Radon變換被廣泛地應用于多次波壓制(Foster and Mosher,1992;熊登等，2009；鞏向博等，2014；劉菲菲等，2017)及插值重建(Sacchi and Ulrych,1995).Sacchi和Ulrych (1995)提出的利用貝葉斯參數反演求解拋物Radon變換系數方法提高了拋物Radon變換的分辨率，有利于提高多次波壓制(Zhang and Wang,2006;Song et al.,2015;Sun et al.,2019)和數據重建效果(劉喜武等，2004；Wang et al.,2019).Johansen(1995)利用二階正交多項式對疊后水平同相軸地震數據進行擬合，正交多項式系數可以表征地震數據振幅隨偏移距變化情況，該方法缺少同相軸走時特征的相關參數，因此該方法針對的是水平同相軸數據，根據此特征，薛亞茹等(2014)將正交多項式引入到Radon變換中，得到具有保幅特征的2D高階Radon變換；唐歡歡和毛偉健(2014)、唐歡歡等(2018，2020)將其推廣到3D，提出基于3D高階Radon變換的地震數據保幅重建方法.在改善積分路徑方面，牛濱華(2001)提出的多項式Radon變換，將積分路徑從線型或拋物型變為2階多項式曲線，提高了淺層雙曲型同相軸數據在Radon域的稀疏程度，該變換的優勢在于不增加計算量的情況下可以對復雜形態同相軸數據進行稀疏表示，但不能同時對線性、拋物型及復雜形態同相軸數據進行稀疏表示；Trad等(2001)提出了將雙曲Radon變換算子和線性Radon變換算子相結合的混合Radon變換，該方法缺少這兩種算子的交叉項無法對復雜同相軸進行精確擬合，且在時間域進行計算效率較低；魯娥和李慶春(2013)將其應用到地震數據去噪中來，但該變換與積分路徑相關的變換參數只有線性項，導致在變換域出現混疊現象.

以上國內外學者分別從積分路徑的形態、計算效率、分辨率以及保幅性方面對Radon變換進行改進，但現有的Radon變換應用于地震數據處理中仍然存在一個問題，即當線性同相軸、雙曲型同相軸以及復雜形態同相軸同時存在時，不同形態同相軸在Radon域系數不能同時達到最佳稀疏狀態，只有同相軸形態和積分路徑一致的數據在Radon域系數才能集中在一點，而其他的系數則是發散狀態，在空間上有一定的延展性，這將降低隨機噪聲壓制效果以及波型分離精度.

針對該問題，本文提出了多路徑Radon變換(Multi-path Radon,M_Radon)，這里我們把積分路徑僅為線性、雙曲型或拋物型的Radon變換稱為單路徑Radon變換，多路徑Radon變換是指對每個同相軸都有線型和拋物型的積分路徑，且具有兩種不同類型的變換參數來與積分路徑相對應，然后利用最小二乘稀疏反演方法對不同形態同相軸自適應匹配最佳積分路徑，得到在Radon域同時聚焦的高分辨率系數.該變換有利于提高隨機噪聲的壓制、面波壓制以及波型分離效果.

1 方法原理

在地震數據處理中，經典拋物Radon正反變換如公式(1a)、(1b)所示(Hampson,1986;Beylkin,1987)，是廣義Radon變換的一種特殊形式，公式中d為地震數據，x為檢波點坐標，q為拋物型積分路徑的曲率，即速度平方的倒數,m為數據在Radon域系數；將積分公式中x2變為x，如公式(2a)、(2b)所示，其中p為斜率，即速度的倒數，公式為線性Radon正反變換，也稱為傾斜疊加.公式(1a)、(1b)、(2a)、(2b)分別為

(1a)

(1b)

(2a)

(2b)

通過線性Radon或拋物Radon變換，理論上可以將t-x域的線性同相軸或拋物型同相軸變換為Radon域的一個點，如圖1所示，圖1a為一合成的線性同相軸，64個接收道，道間距為20 m，4 ms時間采樣率，512個時間采樣點，合成該數據的速度為v=4000 m·s-1，經過線性Radon變換后其Radon域系數如圖1b所示；圖1c為一拋物型同相軸，速度為v=1800 m·s-1，經過拋物Radon變換后其Radon域系數如圖1d所示.從圖中可以看出，t-x域的地震數據經過合適類型的Radon變換后，其Radon域系數都各自集中在一個點附近，從圖1b、d上很容易找到這兩點對應的變換參數分別為p=0.00025 s·m-1，q=3.08×10-7s2·m-2；再利用公式p=1/v和q=1/v2，可以反向計算出t-x域地震數據線性同相軸和拋物型同相軸的速度分別為v=4000 m·s-1和v=1800 m·s-1，與合成模型數據的速度一致，即Radon域系數分布位置具有明確的物理意義.因此，可以利用Radon變換的稀疏性和明確的物理意義特征進行隨機噪聲壓制、波型分離、多次波壓制以及數據重建.

圖1 單軸數據Radon變換效果(a)t-x域線性同相軸；(b)圖(a)數據線性Radon變換結果；(c)t-x域拋物型同相軸；(d)圖(c)數據拋物Radon變換結果.Fig.1 Radon transform result of single-axis data(a)Linear in-phase axis in t-x domain；(b)Linear Radon transform of data in (a)；(c)Parabolic in-phase axis in t-x domain；(d)Radon transform of data in (c).

但是，在實際地震數據中，直達波、折射波和面波的時距曲線為線性同相軸，反射波的時距曲線為雙曲型(經部分NMO后可近似為拋物型)，在使用線性Radon或拋物Radon變換時，不能使所有波型數據在變換域同時達到最佳稀疏狀態，如圖2合成數據所示，為t-x域地震數據，包含線型和拋物型同相軸；其線性Radon變換域系數如圖3a所示，拋物Radon變換域系數如圖3d所示；可以看出，在使用線性Radon變換時，僅有線性同相軸的Radon域系數是聚焦、稀疏的，其他拋物型同相軸Radon域系數并不稀疏；同樣地，使用拋物Radon變換時，稀疏性僅對拋物型同相軸有效；這是因為當地震數據同相軸形態和積分路徑形態不一致時，需要一系列的變換參數和積分路徑組成的基函數來對地震數據擬合，從而在Radon域剖面上一系列連續的p值或q值位置都有系數分布，導致系數不是稀疏的，且不能從Radon域剖面得到所有同相軸的速度信息.圖3b、e分別是從Radon域系數反變換回時空域的數據；圖3c、f分別為經過不同變換后的數據與原始數據的差剖面，可以看出拋物Radon變換對線性同相軸有一定的正反變換誤差，特別是在同相軸的起始位置；用公式(3)來計算這兩種變換的相對均方誤差：

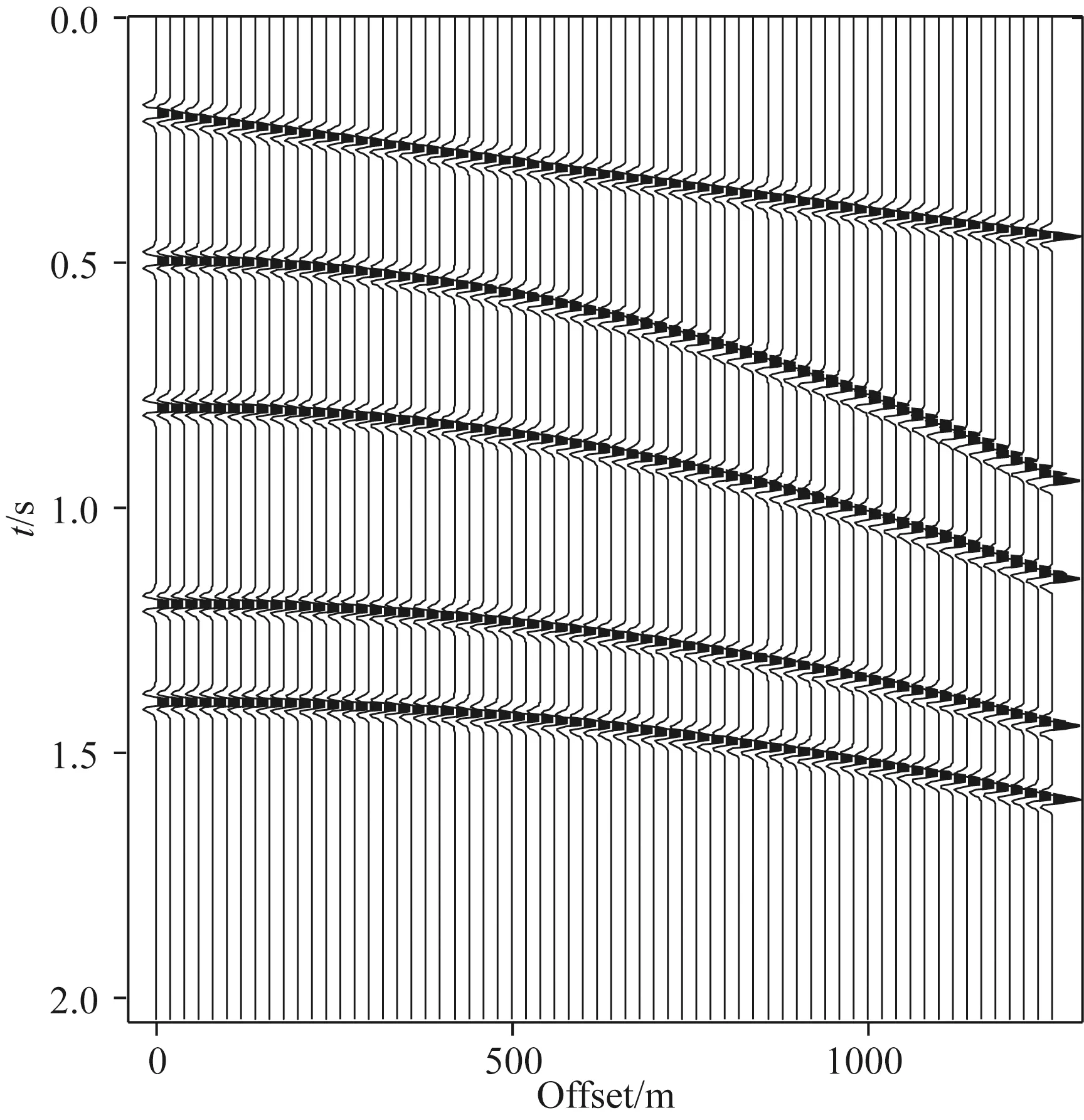
圖2 線性和拋物型同相軸同時存在的地震數據Fig.2 Seismic data with linear and parabolic events

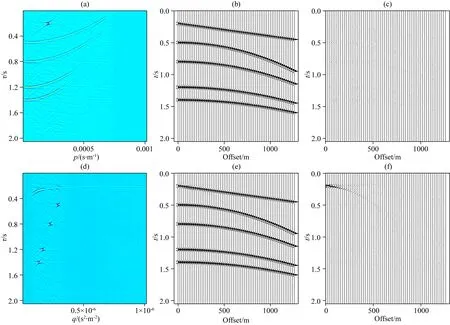
圖3 圖2中地震數據Radon變換效果(a)線性Radon正變換系數；(b)線性Radon反變換數據；(c)線性Radon變換誤差剖面；(d)拋物Radon正變換系數；(e)拋物Radon反變換數據；(f)拋物Radon變換誤差剖面.Fig.3 Radon transform of seismic data in Fig.2(a)Coefficients of linear Radon forward transform；(b)Data of inverse linear Radon transform；(c)Error of linear Radon transform；(d)Coefficients of parabolic Radon inverse transform；(e)Data of inverse parabolic Radon transform；(f)Error of parabolic Radon inverse transform.

(3)

本文提出的多路徑Radon變換能解決該問題，其正反變換公式為

(4a)

(4b)

式中的積分路徑既包含線性項又包含拋物型項，線性Radon變換參數p和拋物Radon變換參數q同時存在；因此，對于含有線型的直達波、折射、面波及雙曲型反射波(可近似為拋物型)的地震數據，多路徑Radon變換可以看作線性Radon基函數和拋物型Radon基函數的組合.選擇p=0基函數，公式(4)可以對拋物型同相軸進行稀疏表達；選擇q=0的基函數，公式(4)可以對線性同相軸進行稀疏表達；而p和q都不為0的基函數，表示公式(4)的積分路徑為多項式，可以對時距曲線不是標準的線型或拋物型同相軸進行擬合.

和傳統Radon變換一樣，多路徑Radon變換也將在頻率域通過反演方法來求解Radon域系數m，對公式(4a)、(4b)作Fourier正變換，即得到頻率域多路徑Radon變換公式為

(5a)

(5b)

根據指數函數的性質，公式(5)可以進一步分解為

(6a)

(6b)

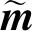
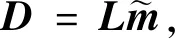
(7)

(8)

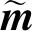
(9)

(10)

可以通過加權迭代方法(Sacchi,1997)進行近似求解.

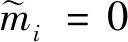
(11)

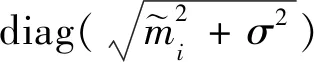
(12)

(13)

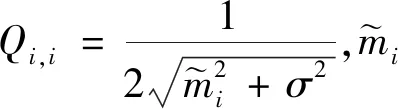
2 模型數據測試

2.1 多路徑Radon變換的稀疏表示能力分析

用多路徑Radon變換對圖2中的數據作正變換，線性積分路徑參數p的最小值p0=0 s·m-1，采樣間隔dp=2×10-5s·m-1，采樣個數np=12；拋物型積分路徑參數q的最小值q0=0 s2·m-2，采樣間隔dq=2×10-8s2·m-2，采樣個數nq=21，3次迭代求解多路徑Radon域系數；系數分布如圖4所示，圖中有12列，分別表示積分路徑參數取值為(p0,[q0,q1,…,q20])，(p1,[q0,q1,…,q20])，…,(p11,[q0,q1,…,q20])時的多路徑Radon域系數，縱坐標表示時間，橫坐標表示拋物型積分路徑參數.從圖4中可以看出，與傳統Radon變換不同(圖3a、d)，多路徑Radon域系數可以同時聚焦，且獨立分布在兩個不同區域上，即圖4中紅色方框標識出的第1列及第11列區域.第一個區域是線性積分路徑參數p=0×dp區，此時p=0，表示積分路徑為拋物型，為q剖面，該區域的Radon系數有4個，分別對應了4個拋物型積分參數，能夠與圖2中時空域四個拋物型同相軸的起始時間、速度一一對應；第二個區域是線性積分路徑參數p=10×dp區，該區域的Radon系數有1個，對應的拋物型積分路徑參數q=0×dq，表示積分路徑為線性，為p剖面，該位置的Radon系數與圖2中時空域線性同相軸起始時間、速度一一對應，且速度可由線性積分路徑參數p=10×dp計算得到；因此，通過多路徑Radon不僅可以使時空域不同形態的同相軸在Radon域系數同時達到稀疏狀態，而且能夠很容易地識別這些系數對應的時空域同相軸形態、時間截距以及速度.這些優勢有助于提高利用Radon變換方法進行隨機噪聲壓制、面波壓制以及波型分離等技術的處理效果.將多路徑Radon域系數通過反變換，我們即可得到時空域地震數據，如圖5a所示，變換誤差剖面如圖5b所示，利用公式(3)計算得到相對均方誤差為1.36×10-4，誤差極小，這是該變換能夠用于地震數據處理的基礎.

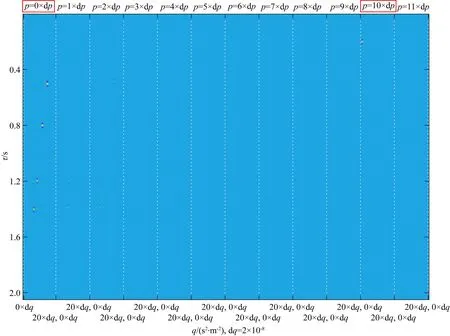
圖4 多路徑Radon正變換系數Fig.4 Coefficients in multi-path Radon forward transform

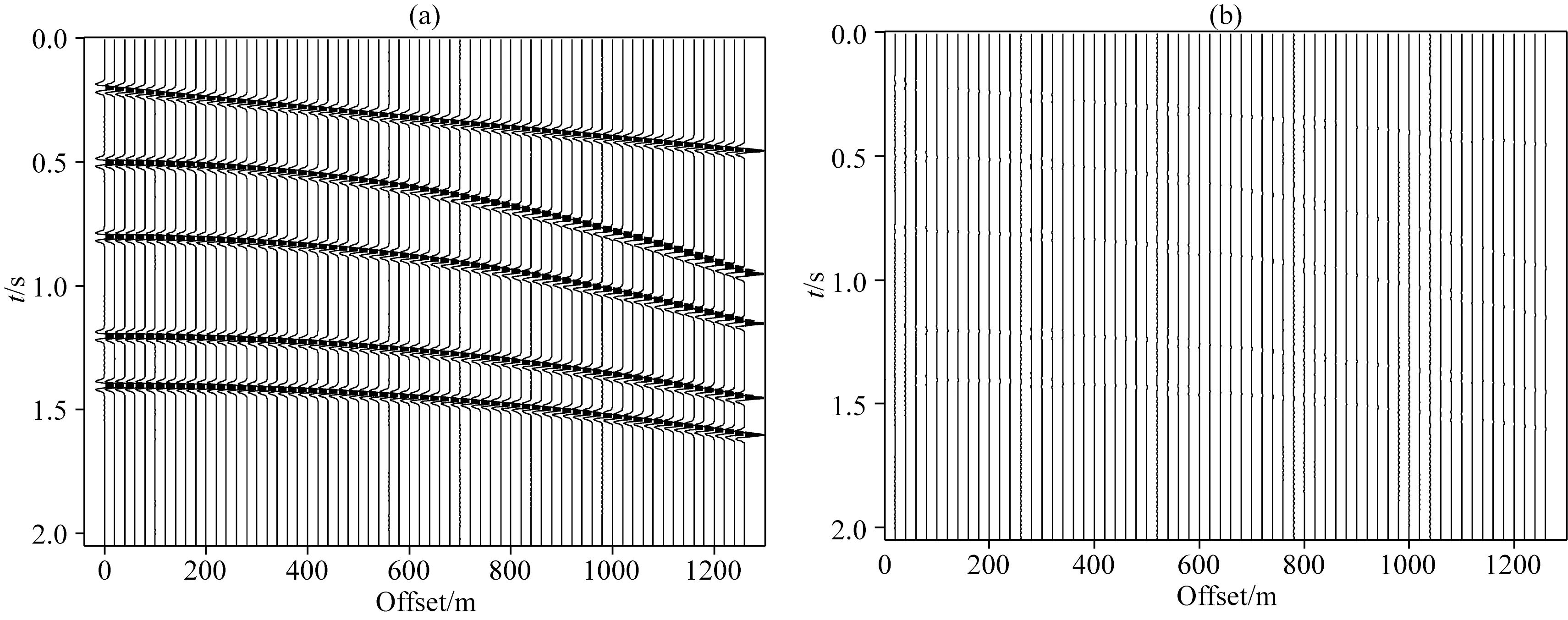
圖5 多路徑Radon反變換結果(a)反變換結果；(b)誤差剖面.Fig.5 Result of multi-path Radon inverse transform(a)Result of inverse transform；(b)Error.

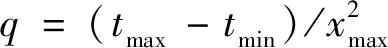
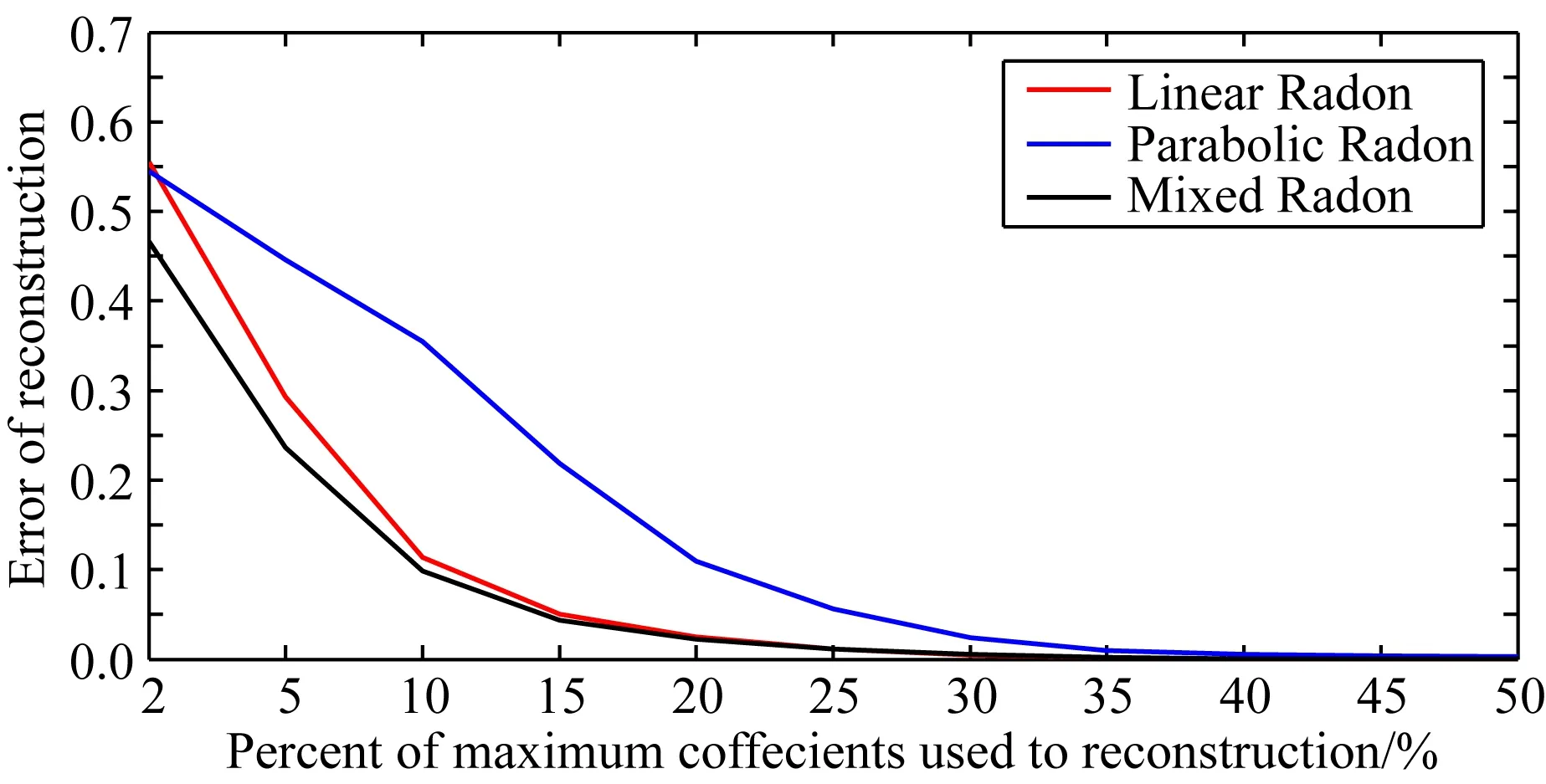
圖6 三種變換的稀疏表示能力Fig.6 Sparse representation capability of three Radon transforms

2.2 多路徑Radon變換在模型數據隨機噪聲壓制及波型分離中的應用

多路徑Radon變換的強稀疏表示能力使其在隨機噪聲壓制和波型分離問題中具有天然優勢，先以模型數據為例進行展示.圖7a為干凈的原始數據，包含待分離的線性和拋物型兩個同相軸，同相軸在遠偏移距形態接近且有重疊.地震數據共有64道，道間距為20 m，每道有300個時間采樣點，采樣間隔為4 ms.將采取常用的傅里葉變換(FK)、傳統的線性Radon、拋物Radon以及本文提出的多路徑Radon變換方法對其進行分離.圖7b、c分別為該數據在線性Radon變換域和拋物Radon變換域的系數分布圖，可以看出在線性Radon變換中僅有線性同相軸的系數分布是稀疏、聚焦的，如圖7b中白色箭頭所示，而拋物性同相軸的系數分布在空間上具有延展性，使二者的系數有部分重疊，很難將其完全分離開來；類似的情況也出現在拋物Radon變換系數中，如圖7c所示；圖7d、e、f分別為線性同相軸的FK譜、拋物同相軸的FK譜以及二者混合一起后的FK譜，很明顯這兩個軸的FK譜能量差異極大，重疊在一起后的FK譜中這兩個軸的能量也有部分重疊，同樣也不能將其完全分離開；圖7g為多路徑Radon域系數，可以看出線性同相軸和拋物同相軸的系數分布在不同區域且同時稀疏、聚焦，很容易將其分離.

圖7 時空域數據在不同變換域系數(a)原始數據；(b)線性Radon變換域系數；(c)拋物Radon變換域系數；(d)線性軸FK譜；(e)拋物軸FK譜；(f)原始數據FK譜；(g)多路徑Radon變換域系數.Fig.7 Coefficients of temporal-spatial data in different transform domains(a)Original data；(b)Coefficients in linear Radon transform domain；(c)Coefficients in parabolic Radon transform domain；(d)FK spectrum of linear event；(e)FK spectrum of parabolic event；(f)FK spectrum of original data；(g)Coefficients of multi-path Radon transform domain.

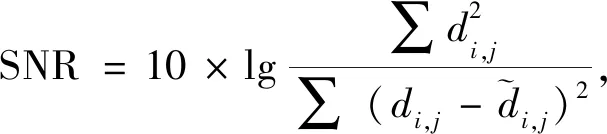
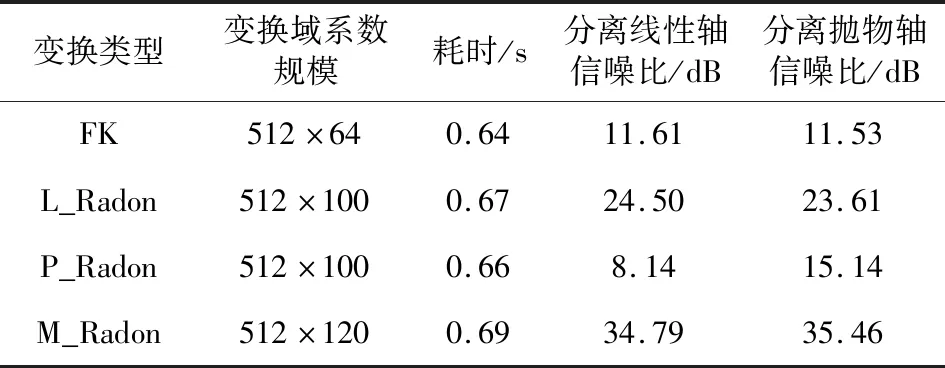
表1 四種變換波型分離效果比較Table 1 Comparison of data separation by 4 transforms

為了測試本文方法抗噪能力，在圖7a原始干凈數據上添加了一定的隨機噪聲，數據的信噪比為-16.09 dB，如圖9a所示.根據上文三種變換的稀疏表示能力曲線來確定噪聲壓制的閾值，首先將圖7變換域中前30%的強能量系數保留，其他系數進行壓制，再進行下一步的分離.我們比較了本文提出的多路徑Radon變換與傳統線性Radon、拋物Radon變換方法的去噪效果.圖9b、c分別為數據在線性Radon、拋物Radon變換域系數，可以看出，由于隨機噪聲的存在，使得線性同相軸和拋物同相軸的變換域系數更加難以區分，進而影響下一步的分離；圖9d為數據在多路徑Radon變換域系數，可以看出，即使存在能量較強的隨機噪聲，由于不同類型同相軸在該變換域系數都同時稀疏、聚焦，從而仍然能夠較容易將其區分并分離；線性Radon變換方法的噪聲壓制及波型分離結果如圖8e、f所示，拋物Radon變換方法的噪聲壓制及波型分離結果如圖9g、h所示,本文提出的多路徑Radon變換方法的噪聲壓制及波型分離結果如圖9i、j所示，從圖中可以很明顯看出，線性Radon變換僅對線性同相軸的噪聲壓制效果較好，拋物Radon變換僅對拋物同相軸的噪聲壓制有效，而多路徑Radon變換方法對線性同相軸和拋物同相軸的分離及噪聲壓制同時有效，同相軸分離完全、無振幅損失且噪聲壓制干凈.三種方法噪聲壓制及分離后數據的信噪比如表2所示，本文提出的多路徑Radon變換方法在去噪及分離后，信噪比達到28 dB左右，與原始-16.09 dB含噪數據相比，信噪比提高了44 dB，其效果明顯優于線性Radon和拋物Radon變換.

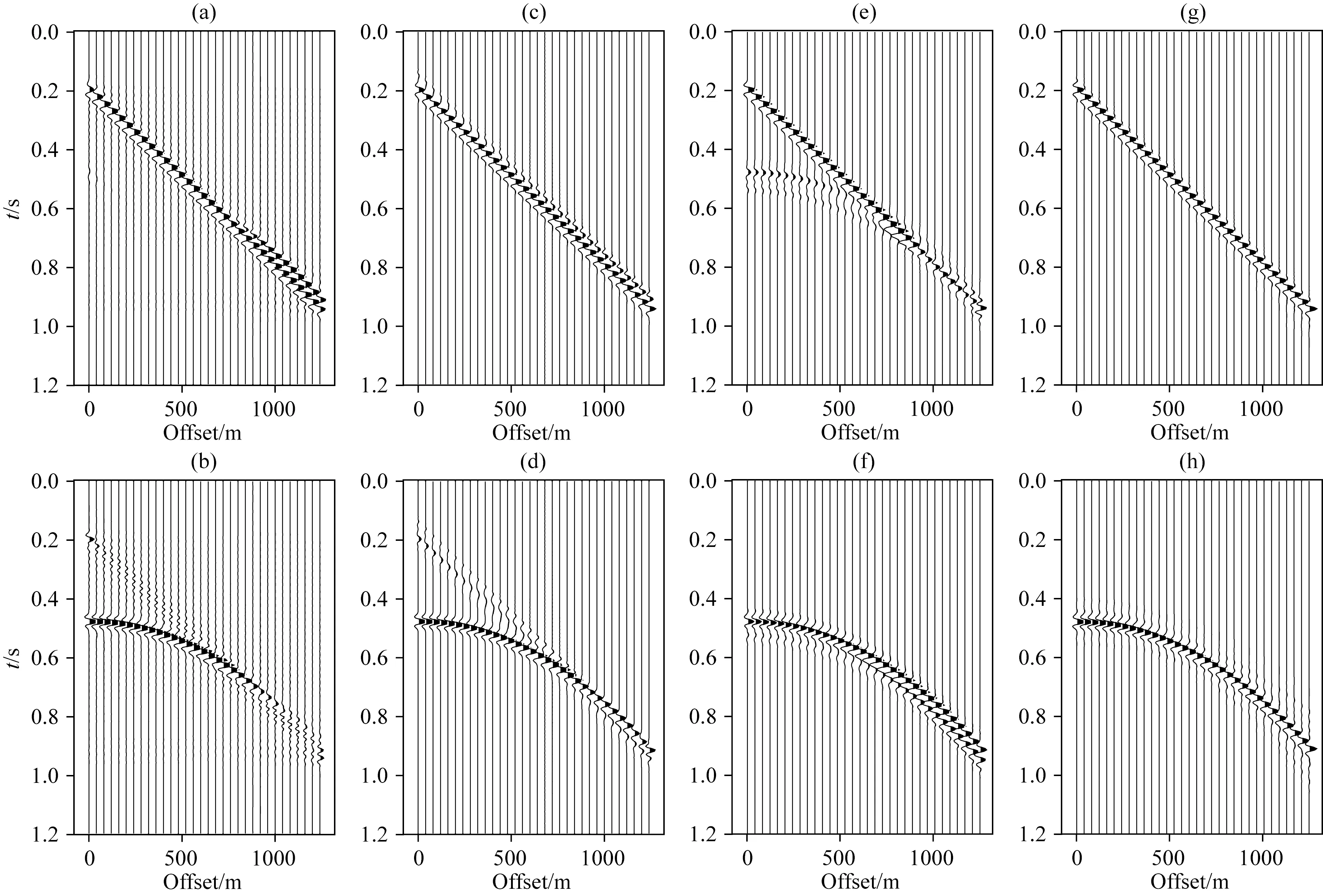
圖8 波型分離效果(a)(b)傅里葉變換波型分離后的數據；(c)(d)線性Radon變換波型分離后的數據；(e)(f)拋物Radon變換波型分離后的數據；(g)(h)多路徑Radon變換波型分離后的數據.Fig.8 Waveform separations by different transforms(a)and (b)Fourier transform；(c)and (d)Linear Radon transform；(e)and (f)Parabolic Radon transform；(g)and (h)Multi-path Radon transform.

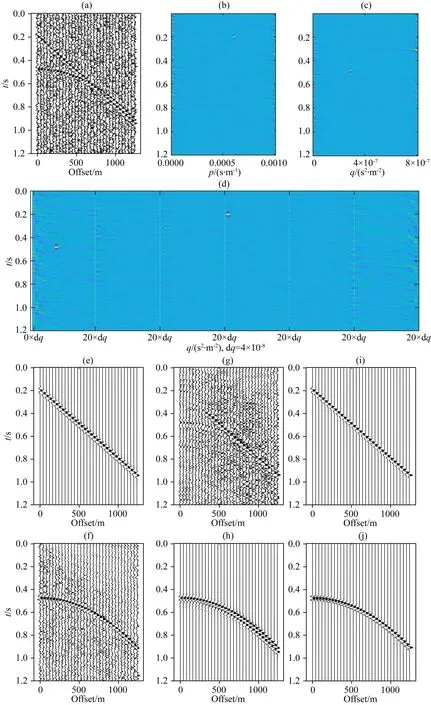
圖9 去噪及分離效果(a)含噪數據;(b)線性Radon變換系數;(c)拋物Radon變換系數;(d)多路徑Radon變換系數;(e)(f)線性Radon變換去噪及分離結果;(g)(h)拋物Radon變換去噪及分離結果;(i)(j)多路徑Radon變換去噪及分離結果.Fig.9 Denoised and separated data by multi-path Radon transform(a)Noised data；(b)Coefficients of linear Radon transform；(c)Coefficients of parabolic Radon transform；(d)Coefficients of multi-path Radon transform；(e)and (f)Denoised and separated data by linear Radon transform；(g)and (h)Denoised and separated data by parabolic Radon transform；(i)and (j)Denoised and separated data by multi-path Radon transform.

表2 含噪數據噪聲壓制及波型分離效果比較Table 2 Comparison of denoised and separated data by three Radon transforms

2.3 多路徑Radon變換在實際數據噪聲壓制及波型分離中的應用

現將該方法應用于塔里木某區域采集的實際數據面波壓制測試中，如圖10a所示，共71道，道間距為30 m,每道625個時間采樣,采樣間隔為4 ms，強烈的面波表現為線性，將近偏移距的有效信號湮沒.根據上文模型數據的測試結果，可以發現在線性和拋物型同相軸同時存在的地震數據中，線性Radon變換的處理效果優于拋物Radon變換，因此在實際數據面波壓制測試中，將僅提供線性Radon和本文提出的多路徑Radon變換的處理效果對比.二者面波壓制效果分別如圖10b、c所示，從圖中可以看出這兩種方法都能夠將線性面波壓制，但多路徑Radon變換方法能夠得到分辨率更高的近偏移距反射波同相軸，如圖中A白色橢圓區域所示；同時，對于深層較弱信號，如2.4 s深度B白色橢圓區域所示，本文方法恢復的同相軸更為連續；從去除的面波數據圖10e、f中紅色箭頭處，可以進一步發現線性Radon變換方法去除了更多有效信號.

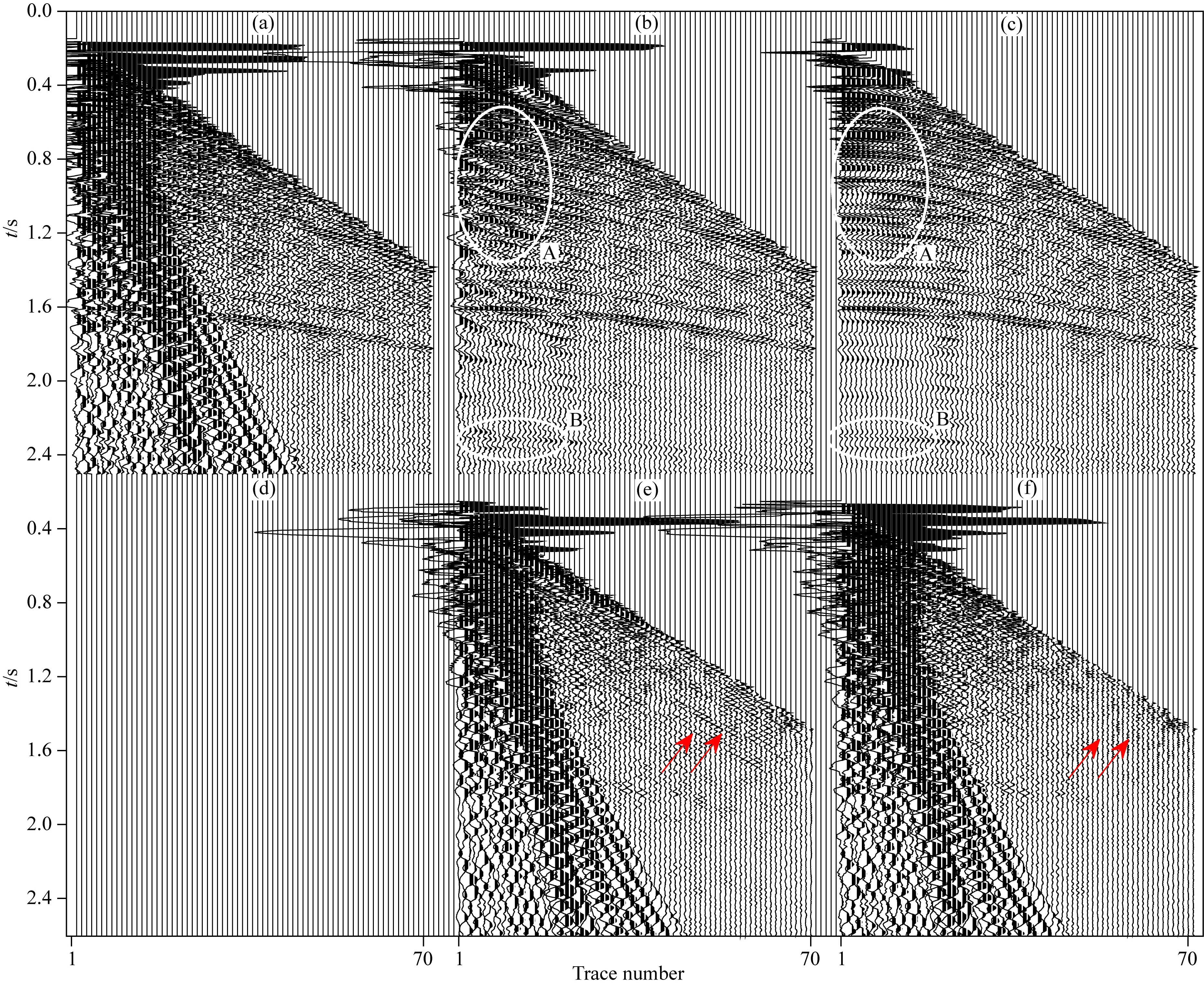
圖10 面波壓制效果(a)原始數據；(b)線性Radon變換面波壓制結果；(c)多路徑Radon變換面波壓制結果；(d)留白區域；(e)(f)分別為(b)(c)去除的面波.Fig.10 Suppression of surface waves by different transforms(a)Original data；(b)Linear Radon transform；(c)Multi-path Radon transform；(d)Whitespace；(e)and (f)Surface waves removed by (b)and (c),respectively.

接著將多路徑Radon變換方法應用于VSP數據的上下行波分離中，原始VSP數據如圖11所示，該數據共201道，道間距為20 m，每道1905個時間采樣，采樣間隔為4 ms，該數據較為復雜，每個同相軸都不是標準的線性或雙曲型.圖12為三種Radon變換方法的上下行波分離效果：圖12a、b分別為線性Radon變換方法分離的下行波和上行波；圖12c、d分別為拋物Radon變換方法分離的下行波和上行波；圖12e、f分別為多路徑Radon變換方法分離的下行波和上行波.可以看出，多路徑Radon變換方法的分離效果最佳，能夠實現上下行波的有效分離；線性Radon變換方法次之，其振幅存在一定的損失，且在上下行波的起始交叉點位置有部分假頻，如圖12a、b中紅色箭頭位置所示；拋物Radon變換方法的效果最差，在近偏移距處傾角較大的同相軸沒有得到有效恢復，且存在拋物型腳印，如圖12c、d中紅色虛框處所示；圖13為近偏移距0～1000 m數據分離效果的放大圖，可以更明顯地看出多路徑Radon變換方法上下行波分離的更為徹底且無信號損失，該實例進一步顯示了本文方法的有效性.

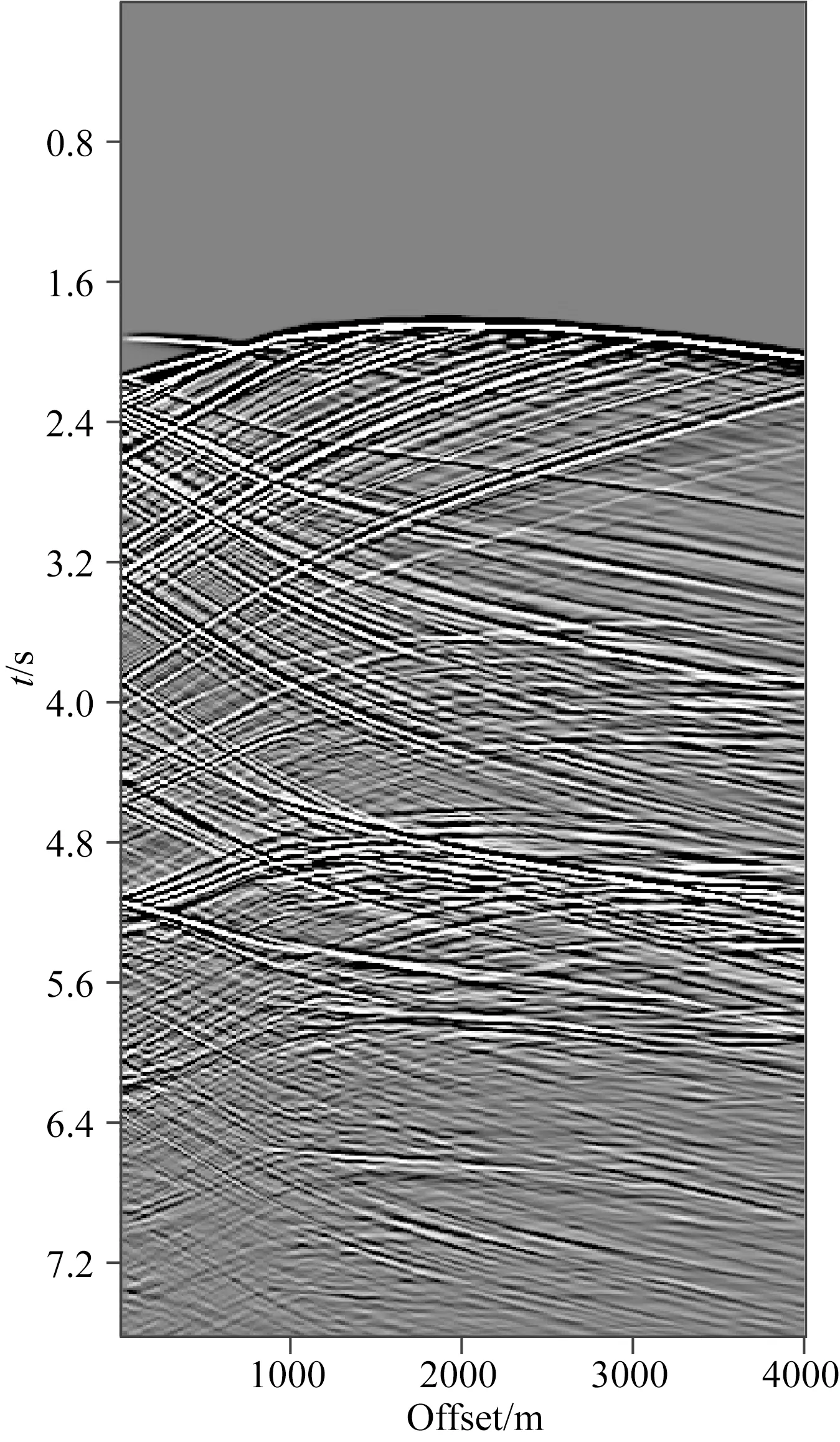
圖11 原始VSP數據Fig.11 Original VSP data

圖13 VSP數據上下行波分離近偏移距放大效果(a)(b)線性Radon變換近偏移距分離效果；(c)(d)拋物Radon變換近偏移距分離效果；(e)(f)多路徑 Radon變換近偏移距分離效果.Fig.13 Enlargement of separation of near-offset upward and downward waves in VSP data (a)and (b)Linear Radon transform；(c)and (d)Parabolic Radon transform；(e)and (f)Multi-path Radon transform.

3 結論

本文提出的基于最小二乘稀疏反演多路徑Radon變換方法，能夠使不同形態同相軸的Radon域系數自動分離，且保持系數的稀疏性.該方法解決了在地震數據中同時存在線性和拋物型同相軸時，傳統Radon變換域系數不能同時準確地進行稀疏表達的問題.本文從變換的稀疏程度、計算效率以及處理效果方面做了詳細的分析，與傳統線性Radon、拋物Radon相比，在不增加額外計算量的情況下，多路徑Radon變換能夠更好地識別不同系數所對應的同相軸形態、時間截距以及速度.這些優勢使Radon變換在隨機噪聲壓制、面波壓制以及波型分離中獲得更佳的處理效果.

需要注意的是，在地質結構特別復雜區域，地震剖面中的同相軸不滿足線性及雙曲型走時特征時，需要采樣間隔較小的p參數和q參數對其進行擬合，即p和q的采樣個數增加，使多路徑Radon變換算子規模成倍加大，從而導致該變換的計算效率降低，且變換域系數不再集中于某些點而是在一定范圍內進行展布，失去稀疏特征.因此，綜合考慮處理效果和計算效率，多路徑Radon變換在同相軸有明顯線性和雙曲型形態的地震數據中更具優勢.

致謝感謝評審專家提出的中肯意見和建議，使論文得以完善和豐富.