例說“數學的眼光”

郜舒竹 馮林

【摘? ?要】我國數學課程與教學的一個傳統是重視計算，學習者對于視覺感知和推理的經歷與經驗不足。“數學的眼光”作為數學素養(yǎng)以及數學課程目標的要素之一，在數學教學實踐中得到落實，可以彌補這樣的缺憾。把數學的眼光與視覺感知和推理聯系起來，讓其成為認知主體與外界對象、環(huán)境交往互動的過程與結果，同時將其發(fā)展為人的一種認知能力，具有非常重要的意義。這種能力的強弱會直接影響學生的學習。眼光作為一種認知能力，是需要在數學學習過程中逐步鍛煉并提升的。利用小學數學課程內容中常見的平面圖形面積關系的比較，詳細說明了“數學的眼光”具體、狹義的意義。從教育的角度說，這樣的意義不僅是認知方面的，而且還包括情感意義的鑒賞。

【關鍵詞】數學的眼光;視覺感知;視覺推理;面積;平面圖形

“數學的眼光”被認為是數學素養(yǎng)以及數學課程目標的要素之一。從抽象、廣義的角度說，它可以指向認識事物的思想觀念;從具體、狹義的方面看，它可以指向認知實踐中的過程與方法。為了將數學的眼光落實到數學課程設計與教學實踐中，下面重點討論其具體、狹義的意義，把“眼光（Visualization）”理解為人利用眼睛這一視覺器官“看”的過程與結果，其中既有“視覺感知（Visual Perception）”獲取信息的過程，也有“視覺推理（Visual Reasoning）”生成想法的思維活動[1]。視覺感知主要指看的過程以及形成思維“表征（Representation）”的過程，視覺推理則傾向于感知信息與已有心理“圖式（Schema）”之間相互作用的思維活動。

因此眼光是認知主體與外界對象、環(huán)境交往互動的過程與結果，同時也是一種認知能力，簡單地說就是“如何看”和“看到什么”的能力。這種能力的強弱會直接影響學生的學習，許多學習中產生的困難、誤解和錯誤都與眼光有關，眼光作為一種認知能力，是需要在數學學習過程中逐步鍛煉并提升的。下面以平面圖形的認識以及面積的比較為例進行說明。

一、看不見的“相等”

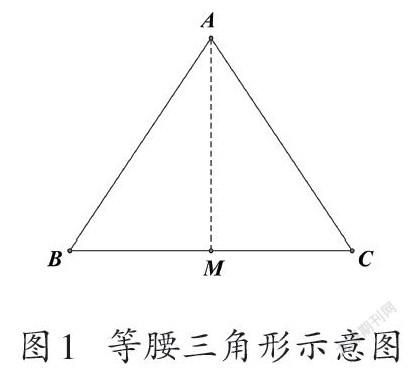
這里的“相等”，更準確的說法是“等價（Equivalence）”，指的是不同圖形之間面積大小的關系。任何一個封閉的平面圖形，都會有“質（Quality）”與“量（Quantity）”兩方面的認知元素，屬于質的元素是形狀、顏色等，屬于量的元素是長度、面積、體積、角度等。如果在平面上畫出一個等腰三角形ABC，將BC邊中點M與頂點A連接成線段AM。那么大三角形ABC就被分為兩個小三角形ABM和AMC（如圖1）。

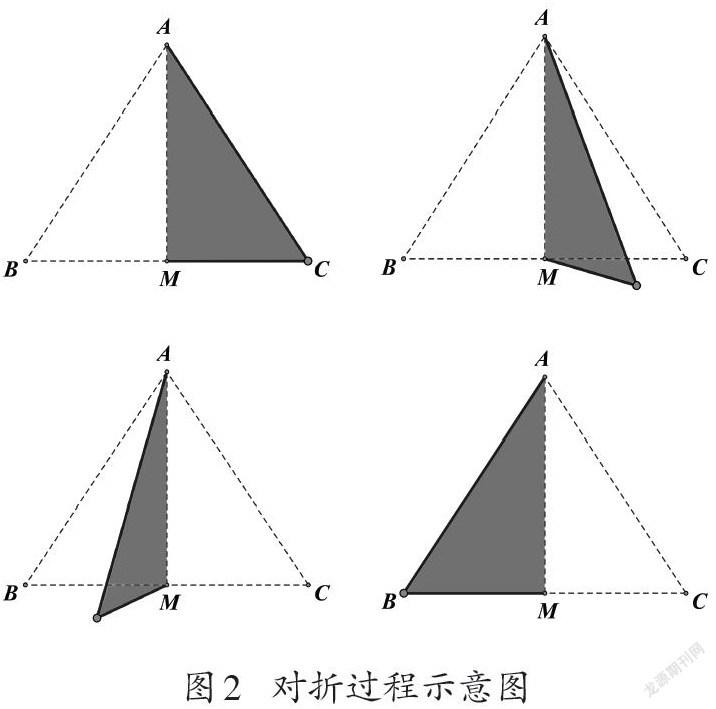
這時通過視覺可以自然地感知到這兩個小三角形的面積是相等的，判斷的依據是兩個小三角形看起來完全相同，也就是“全等（Congruence）”。視覺感知的過程可以伴隨著“具身的（Embodied）”對折動作，如果把大三角形ABC視為一張紙，沿著虛線AM對折后，兩個小三角形可以完全“重合（Superposition）”（如圖2）。

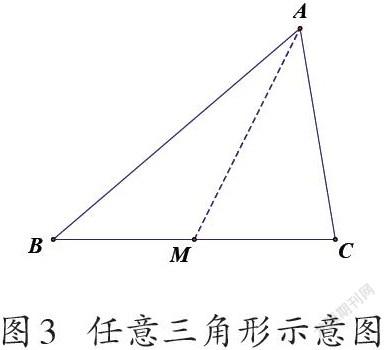
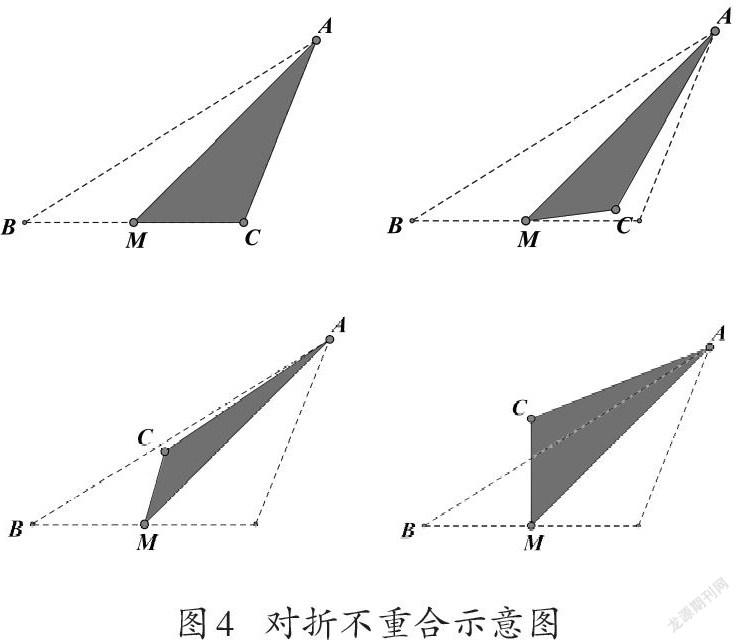
這樣的重合意味著兩個三角形作為量的面積是相等的，同時作為質的形狀是相同的，判斷的依據更傾向于質性的形狀相同。因此可以說，當比較對象質與量的關系一致時，通常不會造成認知困難。進一步，如果將頂點A向右稍加移動，使得整個三角形的形狀發(fā)生變化，呈現出傾斜的狀態(tài)（如圖3），那么兩個小三角形ABM和AMC的形狀就不一樣了，比較的對象出現了“形異”的情況，這時比較三角形ABM和AMC的面積是否相等，視覺感知就會出現困難，因為沿襲前面對折的經驗，無法使得兩個三角形重合（如圖4）。

在對北京一所小學五、六年級學生進行調查后發(fā)現，當學生已經知道三角形面積公式后，多數學生能夠得出兩個小三角形面積相等的結論，依據是“等底等高”。但如果進一步問學生：“除此之外還有什么方法能夠判斷出面積相等？”幾乎無人能夠回答。在對職前、職后教師進行調查后同樣發(fā)現，許多教師也不能回答這樣的問題。

這就反映出數學課程與教學的一個問題，重視公式和計算，輕視針對數學對象進行視覺感知和推理的認知活動。如果把數學教學視為教育的過程，那么提升學生的認知能力自然應當成為數學教學的目的之一。為此就需要在課程設計與教學中，讓學生有機會去經歷視覺感知和推理的過程，通過圖形的運動與建構，使得看不見的關系“可視化（Visible）”。

二、從正方形與長方形說起

小學階段認識平面圖形，通常始于正方形與長方形，而且把正方形視為特殊的長方形。從邏輯分類的角度看，因為正方形具有長方形的所有屬性，因此把正方形視為特殊的長方形是合理的。但從認知的視角看，正方形與非正方形的長方形是存在差異的。下文所說的“長方形”都特指長與寬不等，也即非正方形的長方形。那么這樣的長方形與正方形存在哪些認知方面的差異？

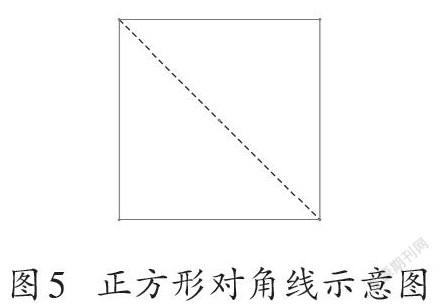
正方形相對于長方形最明顯的特征是四條邊的長度都相等，如果畫出對角線，將正方形分為兩個三角形，那么二者形狀、大小都相同。這樣的性質可以通過沿著對角線對折重合明顯看出（如圖5）。

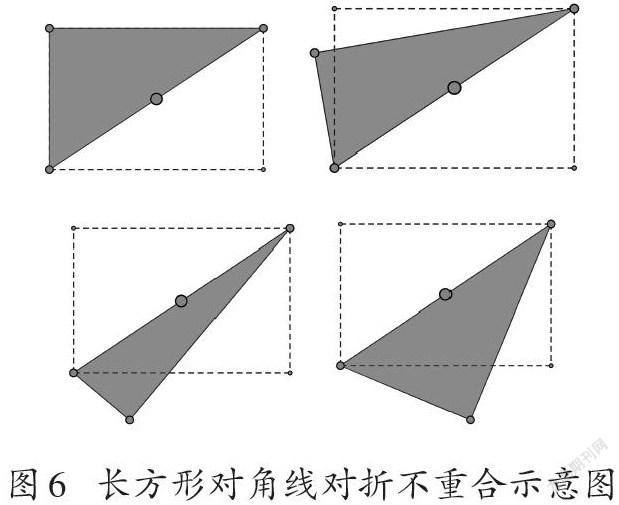
長方形則不同，一條對角線將長方形分為兩個直角三角形，雖然通過視覺可以“感覺（Sensation）”到二者的形狀、大小都相同，但這樣的相同并不能通過沿著對角線對折重合感知到（如圖6）。因此這只是一種感覺，尚未達到感知的水平。

這就表明，長方形與正方形在視覺感知的過程與方法方面存在差異。對折重合體現的是“軸對稱（Axis Symmetry）”的關系，是人類經驗中最熟悉的關系，諸如人的身體、建筑物、植物等許多熟悉的事物，都或多或少地表現出軸對稱的關系，因此是最容易通過視覺感知到的。像長方形對角線這樣，不能使得分出的兩個三角形對折重合，就需要改變視覺感知的方式，這樣的改變自然也是提升認知能力的機會。

如果把對折或對稱看作一種“動態(tài)（Dynamic）”的運動過程，即利用視覺在看的過程中將圖形作了運動，那么這種視覺中的圖形運動，就叫作圖形的“變換（Transformation）”。這樣的運動或變換其實質是思維中的活動，畫在紙上的圖形是靜止的，是觀察圖形的人通過視覺使其發(fā)生了變化，因此這樣的運動也叫作“虛擬運動（Fictive Motion）”，是觀察者對客觀對象運動的想象或思維中的模擬（Simulation）[2]。古希臘歐幾里得的《原本》中對于圖形的全等，就是利用“通過運動可以重合”定義的[3]。某圖形通過運動能夠與另一圖形完全重合，就說這兩個圖形的形狀和大小完全相同，也就是全等。其中的運動其實是虛擬的運動，由于運動過程保持了圖形的形狀和大小不變，因此也叫作“剛體運動（Rigid Motion）”[4]。

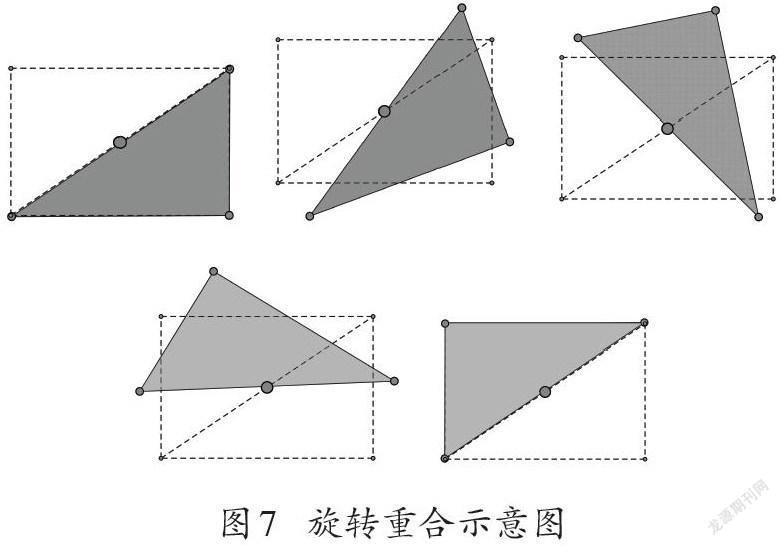
小學數學課程內容中的圖形運動不僅包括對稱，還有平移和旋轉。用旋轉的眼光看長方形對角線分出的兩個三角形（如圖7），最左側的陰影三角形沿著對角線中點，逆時針（也可以順時針）旋轉180度，就與另外一個三角形完全重合。因此運用圖形旋轉的認知方式，就可以感知到長方形對角線所分出的兩個三角形全等。

雖然結論與正方形相同，但視覺感知和推理的過程是不一樣的。正方形可以同時運用軸對稱和旋轉的方式實現重合，而長方形只能運用旋轉的方式。教學中讓學生有機會經歷并辨別這樣的過程差異，對于提升學生的視覺感知能力是十分必要的。接下來進一步看長方形和平行四邊形在認知過程方面的差異。

三、長方形與平行四邊形

平行四邊形對角線所分出的兩個三角形同樣具備形同量等的全等關系。視覺感知和推理的過程與長方形類似，同樣可以通過圍繞對角線中點旋轉180度實現兩個三角形重合（如圖8）。

但二者在軸對稱方面存在差異。對于長方形，如果連接相對兩邊的中點作出直線，那么這樣的直線就成為對稱軸，也就是可以實現分出的兩個小長方形對折重合。但平行四邊形（非長方形，下文同）不具備這樣的軸對稱性，也即相對兩邊中點連線，將大平行四邊形分為兩個小平行四邊形，二者不能實現對折重合（如圖9）。

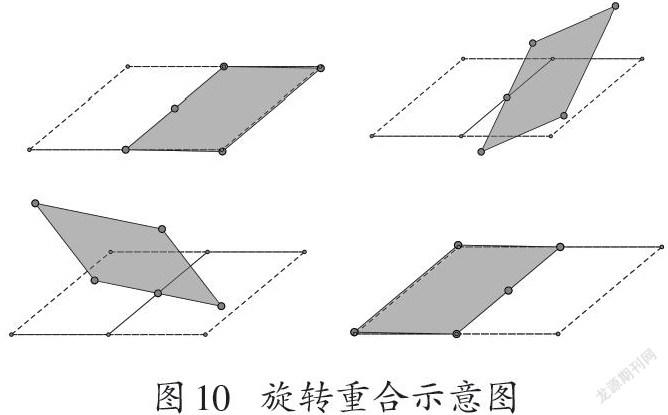
因此非長方形的平行四邊形不具備軸對稱的性質，也即沒有任何一條直線可以成為平行四邊形的對稱軸，而長方形可以通過連接相對兩邊中點得到兩條對稱軸。因此長方形具有軸對稱的性質，平行四邊形不具備這個性質，這是長方形與平行四邊形最大的差別。盡管如此，平行四邊形相對兩邊中點連線所分出的兩個小平行四邊形仍存在全等關系，這樣的關系可以通過旋轉重合看出（如圖10）。

將圖10中的陰影平行四邊形，沿著逆時針（或順時針）方向，繞相對兩邊中點連線的中點旋轉180度，就可以實現兩個小平行四邊形完全重合。至此得到了正方形、長方形和平行四邊形共同的性質：

l對邊中點連線和對角線將圖形分為兩個形狀、大小完全相同的圖形。

從軸對稱的角度說，正方形具有最強的對稱性，有兩條對邊中點連線和兩條對角線作為對稱軸;長方形次之，有兩條相對兩邊中點連線作為對稱軸;平行四邊形沒有對稱軸。從旋轉的角度說，三者都有旋轉中心，可以通過旋轉一定角度實現重合，這樣的圖形也可以說具有“旋轉對稱（Rotational Symmetry）”的性質。旋轉對稱的一個特殊情況，即旋轉180度可以實現重合的兩個圖形，也叫作“中心對稱（Central Symmetry）”或“點對稱”，因此，正方形、長方形和平行四邊形不僅具有旋轉對稱性，也具有中心對稱性。

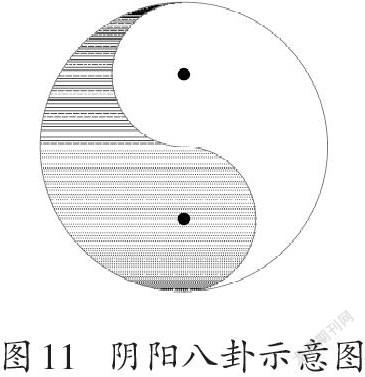
具有旋轉對稱性以及中心對稱性的圖形有很多，如我國經典的“陰陽八卦圖”并非軸對稱，而是一個典型的旋轉（中心）對稱圖形（如圖11），即圖中陰影部分圍繞大圓圓心旋轉180度，就可以與右側部分重合。古今中外藝術作品中，這樣的旋轉對稱現象十分普遍。可以說，“對稱性”是視覺藝術審美的核心要素。

四、回到三角形

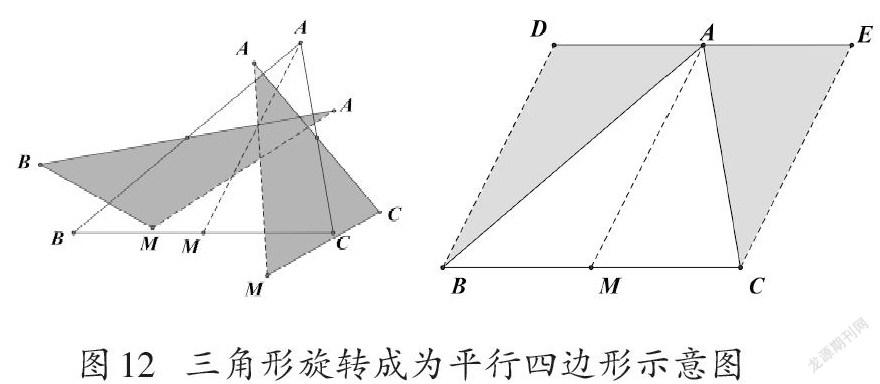
回到文初關于三角形的問題，為了能夠看出圖1中兩個小三角形ABM和AMC面積相等，就需要將“形異”變?yōu)椤靶瓮保簿褪且獙⒁曈X感知和推理方式進行改變，將原圖進行重新建構。從前面的討論可以知道，一個平行四邊形對角線分出的兩個三角形可以通過旋轉實現重合。那么，反過來看，三角形也應當可以通過旋轉形成平行四邊形（如圖12）。

圖12左圖中兩個小三角形ABM和AMC分別繞AB邊和AC邊中點，順時針或逆時針旋轉，就可以形成右圖兩個平行四邊形AMBD和AMCE，并且二者拼接為一個大平行四邊形DECB。也可以通過將線段BM和MC分別向上平移成為DA和AE，線段AM分別向左、右平移，成為BD和CE，同樣得到大平行四邊形DECB。

其中點A和點M分別是大平行四邊形DECB中DE邊和BC邊的中點。根據之前的經驗，線段AM將大平行四邊形DECB分為兩個形狀、大小完全相同的小平行四邊形，因此三角形ABC的兩條邊AB和AC相當于同一個平行四邊形的兩條對角線，自然就說明每個三角形的面積都是同一個平行四邊形面積的二分之一，因此其面積是相等的。三角形一邊中點與對面頂點的連線，叫作這個三角形的一條“中線（Median）”。因此前面通過圖形運動的視覺感知和推理得到的結論可以表述為：

l任意三角形的一條中線所分出的兩個三角形面積相等。

雖然這樣的結論可以通過三角形面積公式以及等底等高的條件輕易得到，但這只是邏輯意義的概念，缺少情感意義的“自然而然”。運用視覺感知“看出來”，使得認知過程和結果更加親切自然，具有了“美學（Aesthetics）”的意蘊，使得認知過程融入了對于對稱現象的鑒賞體驗和愉悅的情感體驗，對于引發(fā)學習動機十分有益。不僅如此，這樣視覺感知和推理的經驗可以使得許多所謂的難題變得顯而易見。2011年國際著名的期刊《數學教育研究》（Educational Study in Mathematics）發(fā)表了一篇對高中學生關于面積守恒認知能力的調查研究報告，發(fā)現多數學生對于下面的問題存在認知困難。[5]

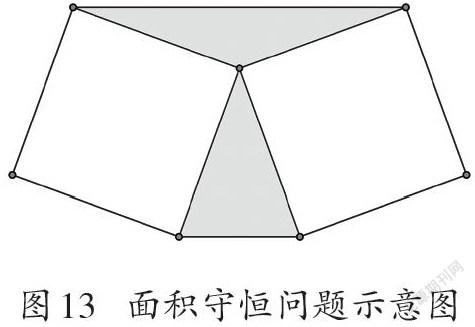
問題：如圖（圖13），兩個相同的正方形有一個共同的頂點，二者之間有兩個三角形（陰影）。這兩個三角形面積相等嗎？

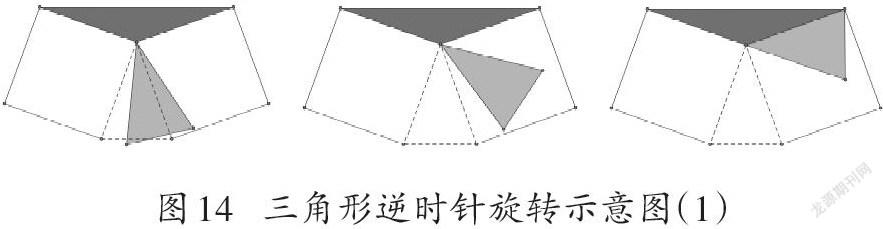
這一問題與前面三角形中線問題類似，兩個三角形形狀不同。不僅如此，二者底邊長度和高的長度也明顯不同，因此三角形面積公式就失去了作用。如果對于平面圖形面積的學習僅僅是“公式+計算”，那么對于這樣的問題自然會束手無策。如果有了前面關于視覺感知和推理的經驗，在視覺中可以將下面小三角形沿著逆時針（或順時針）方向旋轉90度，將兩個三角形拼接成為一個大三角形（如圖14）。

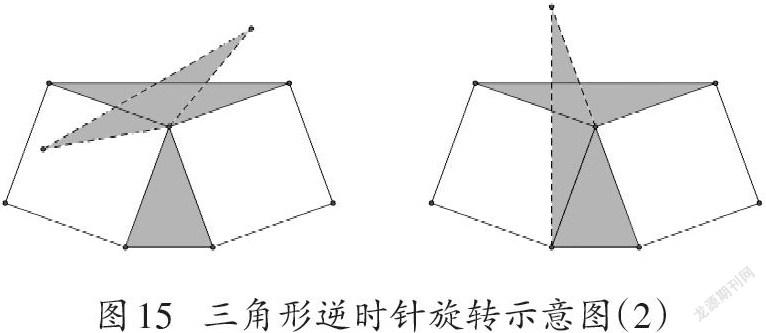
那么這兩個小三角形就是在同一個大三角形中用中線分開的兩個小三角形，其面積自然應當是相等的。此外，也可以將上面的小三角形沿著逆時針（或順時針）方向旋轉90度，再將兩個三角形拼接起來。同樣可以看出二者面積相等（如圖15）。

通過運動將圖形進行重構，是視覺感知和推理的重要方面，這種重構的過程與方法也是多樣的。在對小學六年級學生進行的調查中發(fā)現，有學生利用上、下兩個三角形都是等腰三角形，用豎直線段將兩個三角形平分，然后將下面左側三角形順時針旋轉，右側三角形逆時針旋轉，進而感知到相等關系（如圖16）。

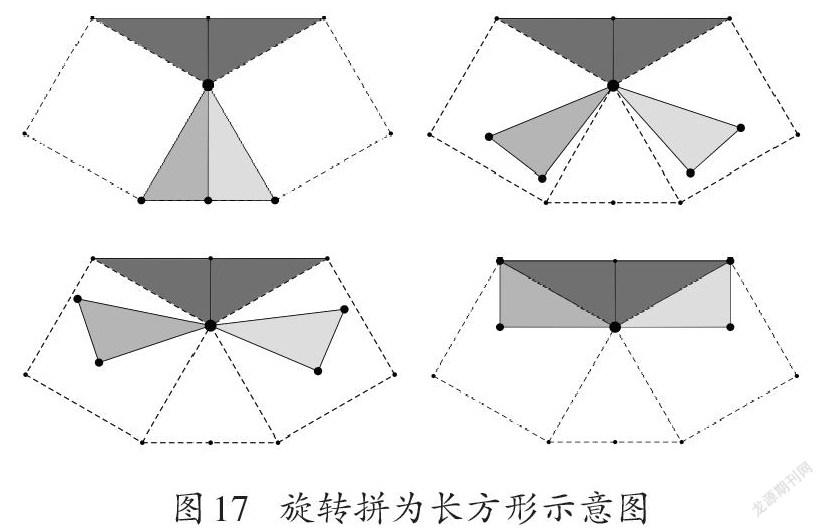
具體來說，就是將下面三角形的左側部分順時針旋轉90度，右側部分逆時針旋轉90度，與上面的三角形拼接成為一個長方形（如圖17）。

這時利用長方形相關性質，相等關系就一目了然了。盡管這樣的視覺感知和推理的過程是依賴直觀感受，并非嚴格的證明，但從素養(yǎng)導向的數學教學的角度來說，這樣的過程對于提升學生視覺感知和推理的能力十分有益，也是圖形認知不可逾越的階段。

小學數學課程中關于平面圖形面積的教學，一般按照長方形（正方形）、平行四邊形、三角形、梯形、圓形的順序進行，依次推導出面積公式，而后運用公式進行面積計算。這樣的課程安排與教學重視的是公式和計算，缺乏關于面積之間關系的感知和推理。因此在課程設計與教學中，應當增加指向視覺感知和推理的學習活動，讓學生在運用眼光“看”的活動中提高視覺感知和推理的能力。

在重視視覺感知學習活動的同時，也應注意其局限性。視覺感知過程中存在著“視覺誤差（Visual Illusion）”，也就是似是而非的現象。比如著名的“桑德平行四邊形（Sander Parallelogram）”，是將一個等腰三角形（圖18右）放在一個傾斜的平行四邊形中（圖18左），這個三角形兩條相等的邊，在視覺中顯得不相等了。[6]

應當相信，任何認知活動都不可能是十全十美的，人的認知過程和認知活動應當是綜合的、多樣的。有視覺感知的活動，就應當伴隨思維的推理和想象的活動;有解釋、證明正確的活動，就應當伴隨辨別謬誤的“證偽（Refutation）”活動。學生只有在這樣豐富多樣的活動中才有可能在各個方面獲得更全面的發(fā)展。如果把人的智力活動概括為以下六點：感覺（Sensation）、感知（Perception）、推理（Reasoning）、想象（Imagination）、象征（Symbolism）、文化（Culture），那么視覺感知和推理是其中最為基礎，也是最為重要的階段。如果把數學中利用公式的計算視為是“量化（Quantitative）”的程序操作，那么視覺感知和推理更偏向于“質性（Qualitative）”的感知和推理，強調“看”的過程和“看出”結果，而不僅是“算”的過程和“算出”結果。這樣“看”的活動和“看出”的能力，不僅可以鍛煉認知能力，而且可以實現對于“美”的情感意義的鑒賞。教師應當在數學學習活動設計中對此引起高度重視，讓學生經歷“看+想+做”的全過程，將培養(yǎng)學生“數學的眼光”真正落實到學生的學習活動過程中。

參考文獻：

[1]NEMIROVSKY R，NOBLE T. On mathematical visualization and the place where we live[J]. Educational Studies in Mathematics， 1997， 33（2）： 99-131.

[2]TEENIE M. Fictive motion as cognitive simulation[J]. Memory & Cognition， 2004， 32 （8）： 1389-1400.

[3]GOODSTEIN R L. Euclidean geometry and the rigid motion group[J]. The Mathematical Gazette， 1953， 37（320）：117-118.

[4]GEORGE K，PANAGIOTIS S，DIONYSSIOS L. Exploring students’ strategies in area conservation geometrical tasks[J]. Educational Studies in Mathematics， 2011， 77（1）： 105-127.

[5]GEORGE W H. Gestalt psychology and mathematical insight[J]. The Mathematics Teacher， 2007， 100（1）： 16-21.

[6]ALEXANDER H B. Living mind： an inquiry into the psychological and logical foundation of human understanding[J]. The Pluralist， 2008， 3（1）：11-88.

（首都師范大學初等教育學院? ?100048）