基于R-L型分數階導數與損耗統計理論的鐵磁材料高頻損耗計算方法

陳 彬 秦小彬 萬妮娜 唐 波

基于R-L型分數階導數與損耗統計理論的鐵磁材料高頻損耗計算方法

陳 彬1,2秦小彬2萬妮娜1,3唐 波1,2

（1. 湖北省輸電線路工程技術研究中心 宜昌 443002 2. 三峽大學電氣與新能源學院 宜昌 443002 3. 國網湖北省電力有限公司宜昌供電公司 宜昌 443002）

傳統損耗統計理論對鐵磁材料的高頻損耗預測誤差較大且存在過高估算的問題。為此，該文首先考慮高頻條件下磁通密度不均勻分布對磁滯損耗的影響，提出基于有限單元剖分法的磁滯損耗計算方法。然后基于R-L型分數階導數對傳統損耗統計理論中的渦流場和渦流損耗計算式進行改進，并引入量子遺傳算法對分數階導數模型中阻尼系數和導數階次進行全局尋優。在上述磁滯損耗、渦流損耗模型以及參數提取方法的基礎上，提出適用于寬頻率、寬磁通密度范圍的改進型損耗統計方法。最后采用愛潑斯坦方圈測量了3% Si-Fe超薄取向硅鋼片在10Hz～10kHz頻率范圍的損耗，將理論計算值與實驗測量值進行對比，結果表明，所提方法在整個頻段內的最大平均相對誤差為9.14%，最小平均相對誤差為2.13%，相比于傳統損耗理論，損耗預測精度大大提高，驗證了該文方法的有效性。

損耗統計理論 磁滯損耗 渦流損耗 分數階導數 量子遺傳算法

0 引言

在中高頻應用工況下，非晶合金、納米晶合金、超薄硅鋼等鐵磁材料具有優異的軟磁性能，是電力電子、航空航天、國防軍工等領域不可缺少的關鍵材料[1-2]。隨著工作頻率的提高，鐵磁材料的能量損耗將顯著增加。為了提高設備的運行效率、能源利用率，需要在了解鐵磁材料損耗機理的基礎上，掌握鐵磁材料在高頻磁化條件下的損耗求解方法。

1892年，C. P. Steinmetz首次提出基于實驗數據擬合的經驗公式法求解鐵心損耗并認為鐵心損耗僅決定于鐵心材料、頻率與峰值磁通密度[3]。Steinmetz經驗公式法雖然具有計算參數少、形式簡便等優點，但本質上屬于現象學模型，缺乏對損耗產生機理的解釋且計算精度較低[4]。為解決上述問題，G. Bertotti基于對巴克豪森跳躍現象描述，提出經典損耗統計理論（Statistical Theory of Loss, STL），將總損耗分離為磁滯損耗、渦流損耗與剩余損耗分量[5]。損耗統計理論具有物理概念清晰，適用于任意波形損耗計算的優點，但鐵磁材料內部磁通密度均勻分布、趨膚效應可忽略的假設條件使得損耗統計理論僅在低頻段適用[6]。文獻[7-8]在損耗統計理論框架下，基于復磁導率與線性磁化法則從麥克斯韋方程中推導出了高頻渦流損耗計算表達式，但這種改進方法僅適用于較低磁通密度下的損耗計算。一些學者將磁滯模型如Preisach模型[9]、Energetic模型[10]與電磁場擴散方程進行耦合[11]，采用有限元法或有限差分法等數值計算方法，獲取了高精度的高頻損耗計算結果。然而，這些數值計算方法在實現過程中會耗費大量的計算時間和存儲空間，磁滯的高度非線性特性也會導致計算結果收斂的不確定性[12]。

近年來，B. Ducharne等將分數階導數引入鐵磁材料的渦流場計算中，實現了鐵磁材料在高頻條件下動態磁滯回線的精確模擬[13]。分數階導數具有時間記憶性與全局相關性的特點，其階數提供了全新的自由度，避免了數值計算方法進行空間離散造成的所需計算時間較長、所需存儲空間較大的問題，保證了高頻動態磁滯回線模擬的準確性，因而被廣泛應用于電磁理論領域。比如：D. Guyomar基于機械干摩擦概念的準靜態磁滯模型與分數階導數結合構造的動態模型用于鐵電材料的動態磁滯行為模擬，取得了良好的效果[14]；Zhang Bin等分別將J-A磁滯模型和Preisach模型與分數階導數組合應用于鐵磁材料的動態磁滯模擬，針對取向晶粒硅鋼鐵磁材料的動態磁滯回線與損耗計算取得了良好的模擬效果[15-16]。然而，上述基于分數階導數的動態磁滯模擬與損耗計算存在如下幾個問題：①在高頻條件下磁通密度呈不均勻分布，磁滯損耗將隨磁化頻率與峰值磁通密度發生變化[17]，基于靜態磁滯模型獲得的單位周期內磁滯損耗與頻率無關，這與實際情況不相符。同時，磁滯模型實現起來較為復雜且需要較大的數據量與計算量[4]。②分數階導數的參數提取（包括分數階導數的階數與阻尼系數）是根據低頻和高頻條件下的磁滯回線數據通過試湊得到，得到的參數值并不能保證為全局最優值。

在傳統損耗統計理論基礎上，本文考慮了高頻條件下磁通密度不均勻分布對磁滯損耗的影響，提出了基于有限單元剖分法的磁滯損耗計算方法。在對R-L型和G-L型分數階導數特點進行分析的基礎上，利用R-L型分數階導數對傳統損耗統計理論中的渦流場和渦流損耗計算式進行改進。引入量子遺傳算法，以渦流損耗計算值與測量值之間誤差最小為目標函數，實現對分數階導數模型中的阻尼系數和導數階次的全局尋優。以3%Si-Fe超薄取向硅鋼片為例，通過愛潑斯坦方圈測量了超薄取向硅鋼疊片的損耗，比較了不同頻率、不同磁通密度下傳統損耗統計模型、基于線性磁化法則的損耗統計模型與基于分數階導數的損耗統計模型的預測精度。近年來，多相電機及其調速傳動系統已成為國內外研究的焦點。

1 傳統損耗統計理論模型

基于損耗統計理論，G. Bertotti提出了鐵磁材料損耗統計模型，將單個周期內的鐵磁材料總損耗t分解為靜態磁滯損耗h、渦流損耗cl和剩余損耗ex，總損耗的表達式為

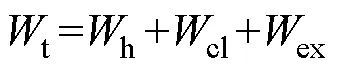
在損耗統計理論框架下，靜態磁滯損耗僅與峰值磁通密度p有關，文獻[18]提出了適用于計算高磁通密度下的磁滯損耗計算式為

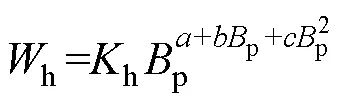
式中，h、、、為參數，可以根據靜態磁滯損耗測量值擬合得到。

在低頻條件下，傳統損耗統計理論基于鐵磁材料內部磁通密度均勻分布的假設條件，根據Maxwell方程推導出渦流損耗的計算式為

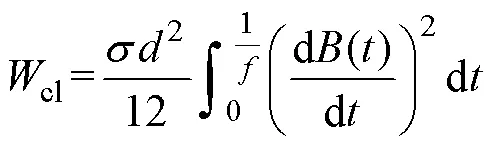
在高頻條件下，趨膚效應顯著，鐵磁材料內部的磁通密密度不再均勻分布。文獻[7-8]基于線性磁化法則，考慮趨膚效應的影響，提出正弦波激勵下的渦流損耗表達式為

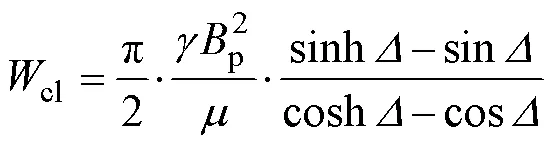
其中

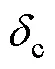
G. Bertotti基于材料內部微觀結構和磁疇結構的隨機統計分布特性推導了剩余損耗計算解析式為

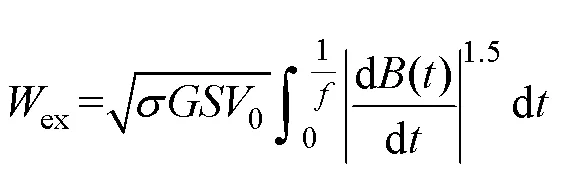
式中，為無量綱數，0.135 6；為鐵磁材料橫截面積；0為表征磁體局部磁場分布的統計參數。

式（2）、式（3）和式（5）所組成的傳統損耗統計理論在低頻條件下對鐵磁材料的損耗預測精度較好，但隨著頻率的升高，趨膚效應顯著，此時鐵磁材料內部磁通密度均勻分布的假設條件將不再適用，進而使得傳統損耗統計理論的損耗預測值與實驗測量值的誤差逐漸增加。為了說明傳統損耗理論所存在的這一固有缺陷，本文基于式（2）、式（3）和式（5）計算了厚度為0.071 9mm的超薄取向硅鋼在磁通密度為0.4T、1T和1.5T下10Hz～10kHz頻率范圍內的損耗，并與測量值進行比較，如圖1a～圖1c所示。由圖1可知，隨著頻率的增加，傳統損耗統計理論的預測值與測量值的誤差逐漸增大，并且預測值明顯高于測量值。

為了將損耗統計理論的應用范圍擴展至寬頻率、寬磁通密度范圍，必須對傳統損耗統計理論進行改進。需要注意的是，文獻[7-8]研究表明，趨膚效應對剩余損耗分量的影響較小，式（5）仍然適用于高頻條件下剩余損耗的預測。

圖1 傳統損耗統計理論的損耗計算值與測量值對比

2 改進的損耗統計理論模型

2.1 基于有限單元剖分法改進磁滯損耗計算模型

在低頻率下，鐵磁材料內部渦流較小，趨膚效應可以忽略。隨著頻率的增加，趨膚效應逐漸明顯，趨膚深度的表達式為

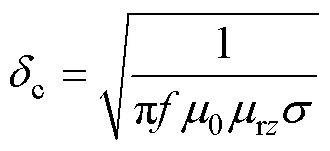
式中，0為真空中磁導率，0=4p×10-7；為硅鋼片的電導率；rz為沿軋制方向的常數相對磁導率。

計及峰值磁通密度對相對磁導率的影響，可以表示為以rz為自變量的多項式，有

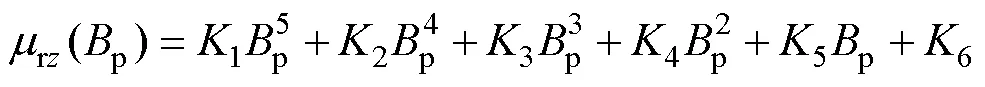
式中，1～6為擬合系數，可以采用沿軋制方向的鐵磁材料磁導率測量值擬合得到。

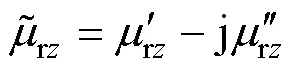
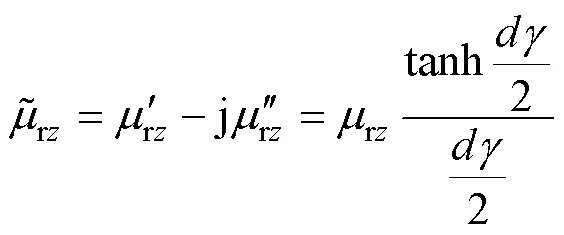
高頻條件下，鐵磁材料內部磁通密度受趨膚效應、復數磁導率、非線性磁化特性等因素的共同影響，沿鐵磁材料厚度方向上各個部分的磁滯回線不同[19]，硅鋼片截面劃分示意圖如圖2所示。假設硅鋼片被劃分為5層區域，從外至內的區域分別編號為1、2、3（即表層為區域1，中心為區域3），記硅鋼片截面上磁通密度為pk（=1, 2, 3），對應區域內產生的渦流為e1、e2。圖2中，為硅鋼片截面寬度，為硅鋼片的厚度，d（=1, 2, 3）為硅鋼片劃分后各層區域的厚度。硅鋼片外表面上的交變磁通密度scos()的方向平行于軸方向，即軋制方向。上述變化影響了單位周期的總磁滯損耗，一個周期內磁滯損耗不再等于一個周期內、相同磁峰密度下的靜態磁滯損耗。精確獲取高頻下磁滯損耗必須考慮鐵磁材料厚度方向的磁通密度分布。

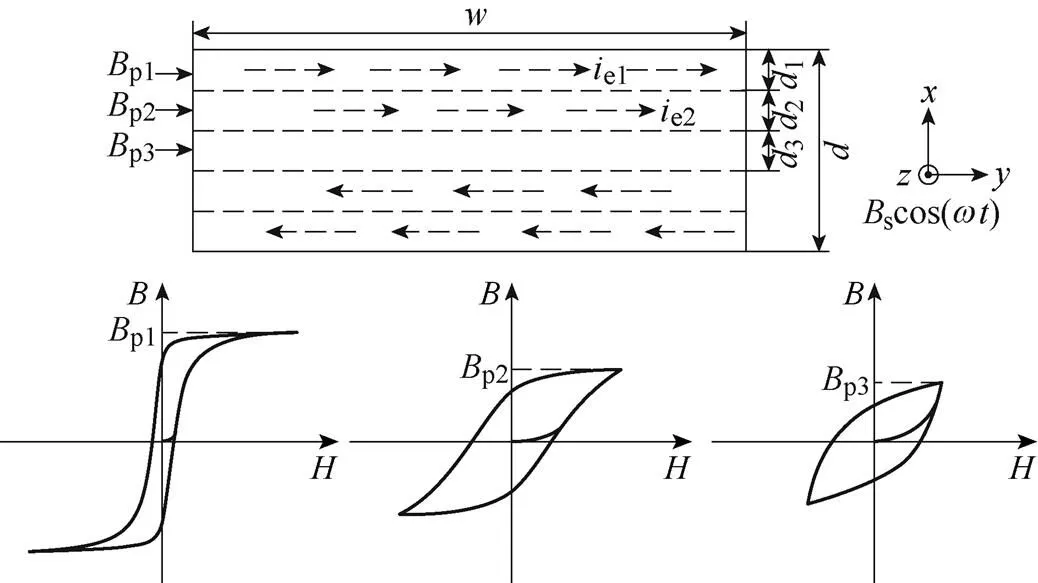
圖2 硅鋼片截面劃分示意圖

硅鋼片厚度方向任意位置處的瞬時磁通密度表達式[19]為

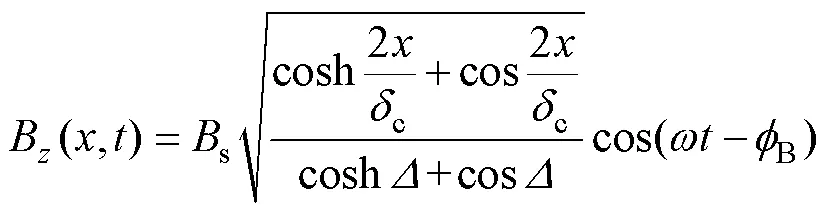
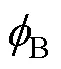
平均峰值磁通密度p與表面磁通密度s的關系為

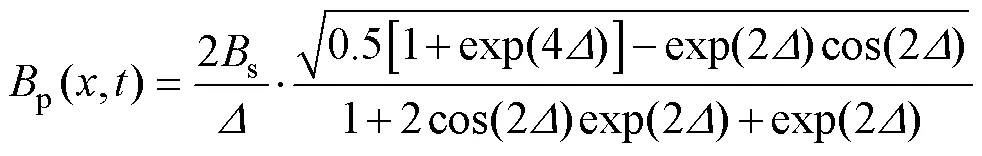
考慮到高頻條件下磁通密度不均勻分布的情況，對磁滯損耗計算式（2）進行了改進，使其能夠適用于高頻條件下磁滯損耗計算。改進步驟為：利用式（8）～式（10）得到給定頻率與表面峰值磁通密度下的磁通密度分布；沿厚度方向上將鐵磁材料劃分為個單元，計算各個單元內部磁通密度pn（=1, 2,…,）。采用式（2）計算各個單元磁滯損耗，總磁滯損耗為各剖分單元磁滯損耗的疊加，有

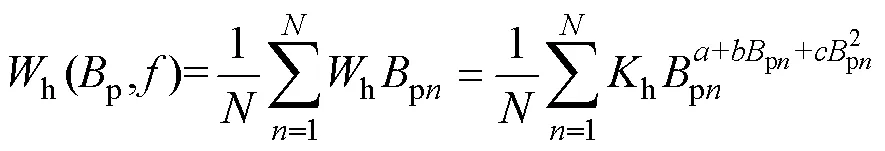
2.2 基于分數階導數的改進渦流損耗計算模型

傳統渦流損耗表達式中含有瞬時磁通密度對時間的整數階導數。整數階導數的局部極限定義不適用于描述非局部、頻率、歷史等依賴性過程[20]。為了避免數值計算方法進行空間離散造成的所需計算時間較長、存儲空間較大的問題，同時能夠考慮渦流損耗對頻率的依賴特性，本文引入分數階導數，實現對高頻渦流損耗的解析建模和計算。

分數階導數將傳統導數的階數由整數推廣至非整數和復數[21]。Grünwald-Letnikov（G-L）型與Riemann-Liouville（R-L）型分數階作為分數階算子的特例，前者表示階導數，后者表示階積分。R-L型分數階是對G-L型分數階的改進與擴展[21]，R-L型分數階所能描述的函數類別比G-L型分數階更加廣泛，G-L型僅能用于描述可積的函數。然而，對于本文所研究的正弦磁通密度函數，兩類分數階導數算子是等價的。因此，本文將依據R-L型分數階導數對傳統損耗統計理論中的渦流場和渦流損耗計算式進行改進，R-L型分數階導數的具體形式[20]為

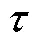
根據場分離假設[22]，渦流場cl與傳統損耗統計理論的渦流損耗cl計算式滿足

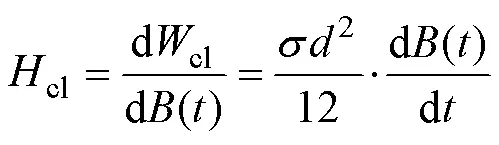
將式（12）引入式（13），可以實現對傳統損耗統計理論中的渦流場的改進，有

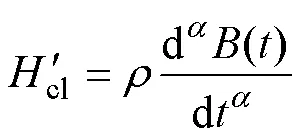
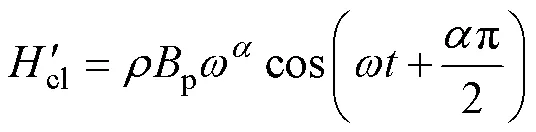
進而得到的基于分數階導數的改進渦流損耗解析計算式，有

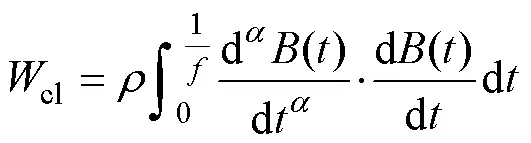
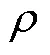
2.3 基于優化算法的分數階參數提取方法

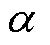
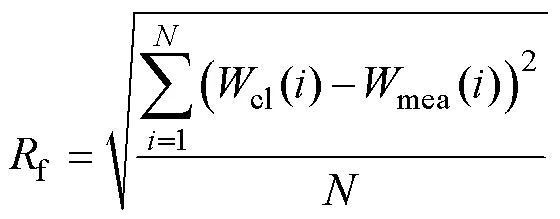
式中，f為方均根誤差；cl為基于式（16）的理論計算值；mea為損耗測量值。

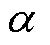
傳統遺傳算法易受交叉、變異概率取值不當影響而產生過早收斂于局部最優解、局部搜索能力弱等問題[25]。量子遺傳算法是量子計算與遺傳算法相結合新興發展起來的概率進化算法。利用量子態的疊加、糾纏和干涉特性，將量子的態矢量引入遺傳編碼，使一條染色體可以表達多個態的疊加，并利用量子邏輯門實現染色體的更新操作，進而實現目標函數的優化與求解。量子遺傳算法既克服了傳統遺傳算法的固有缺陷，同時也保留了其高魯棒性與廣泛適用性等優點。

（1）種群初始化：將不同磁通密度不同頻點的損耗測量值數據點歸為一個種群集合，利用量子遺傳算法函數IntPop產生初始化種群下量子比特應用于染色體的編碼矩陣chrom，有

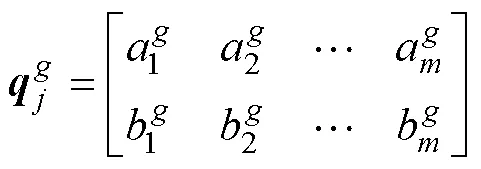
（2）采用collapse函數對種群進行一次測量，獲得確定解集。

（3）基于目標函數（式（17））對()中每個個體進行適應度評估，并作為下一步進化目標值。

（4）對步驟（3）進行循環迭代，并保留()中適應度最優個體及適應度值。

（5）種群迭代次數是否大于最大迭代數，滿足條件計算結束；否則，繼續下一步運算。

（6）實行量子門操作，實現染色體基因的變異進化，從而形成新的種群。量子旋轉門的更新式[26]為

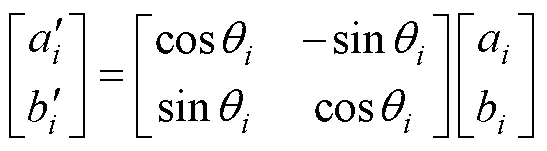
其中

（7）迭代次數加1，返回步驟（3）。

基于量子遺傳算法的分數階導數參數提取流程如圖3所示。

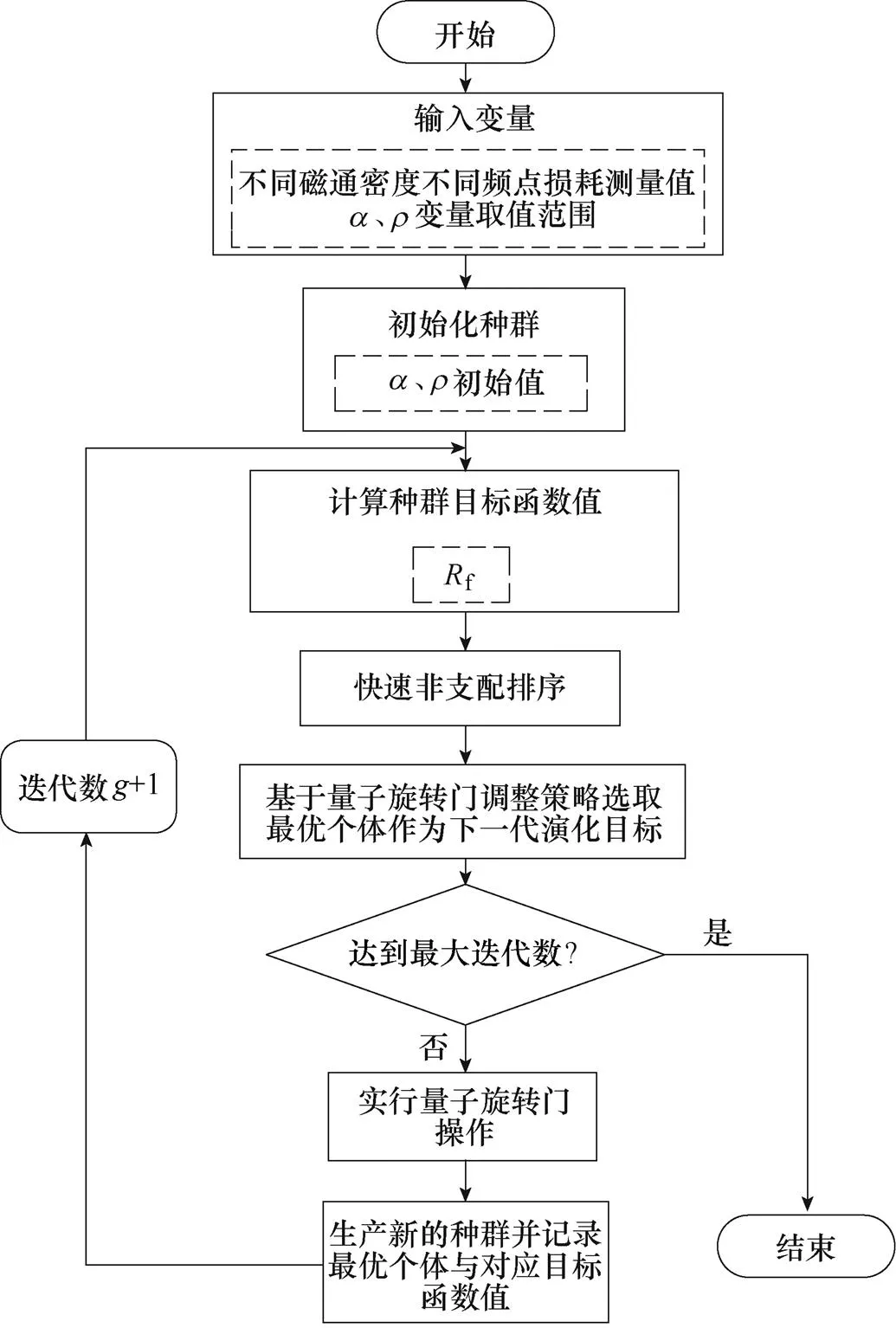
圖3 基于量子遺傳算法的分數階導數參數提取流程

將改進磁滯損耗表達式與改進渦流損耗表達式引入損耗統計理論框架實現對高頻損耗的精確計算。基于有限單元剖分法與分數階導數的改進損耗統計理論計算流程如圖4所示。

3 實驗驗證

3.1 測量系統及參數提取

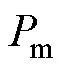
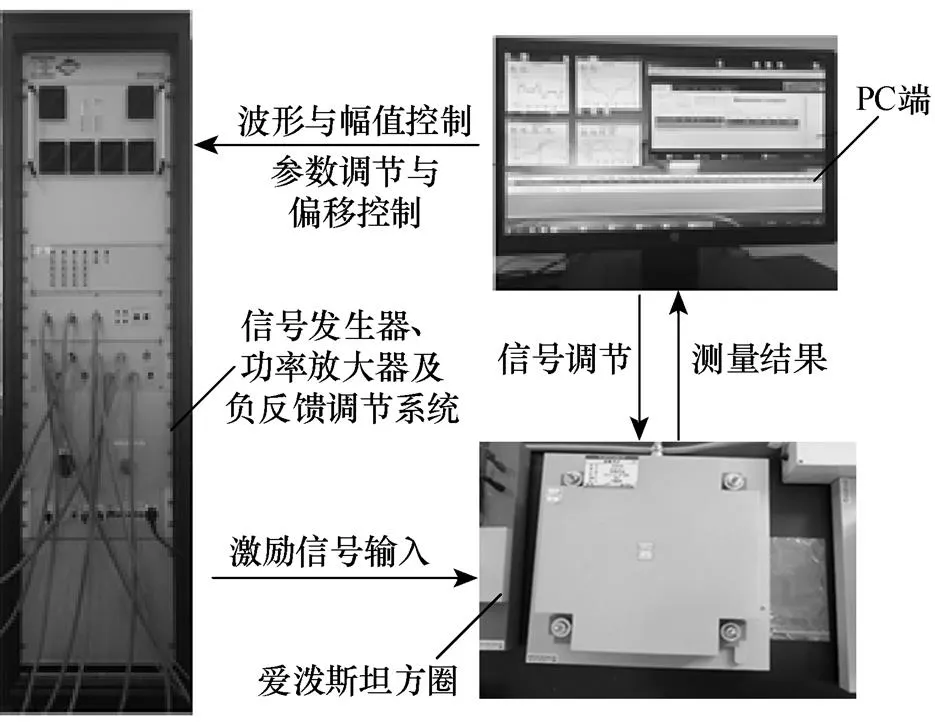
圖5 超薄取向硅鋼片磁特性測量系統

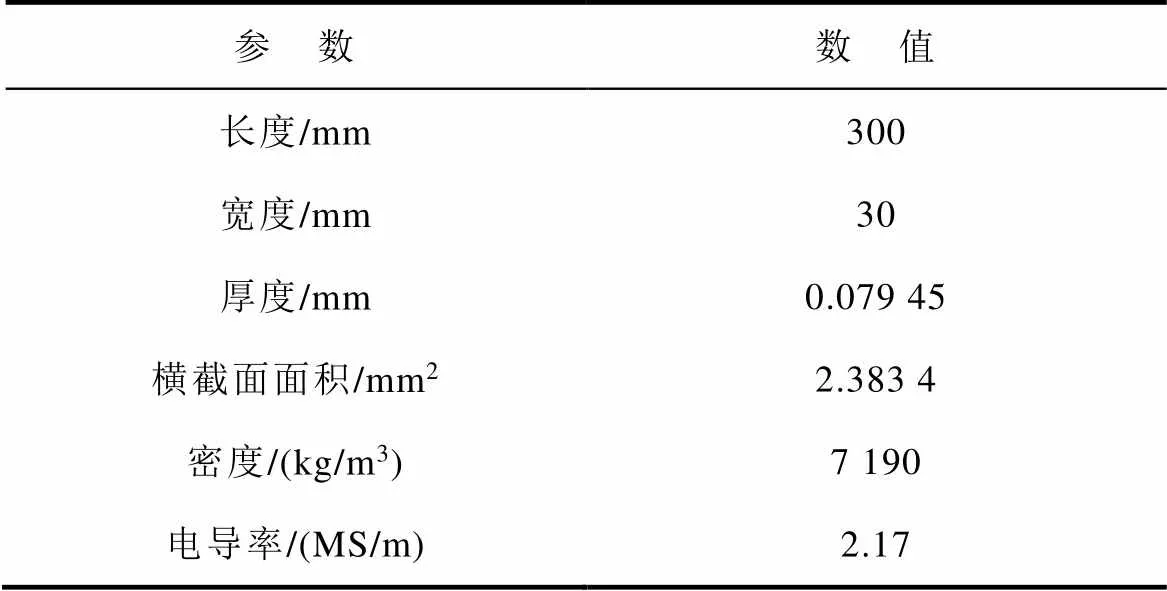
表1 超薄取向硅鋼片樣品參數

式中，m為頻率下動態磁滯回線面積。

單個周期內的磁滯損耗h(p)和剩余損耗中的0可以通過低頻條件下的總損耗測量值t,m(p,)來確定，此時趨膚效應可以忽略。將總損耗測量值t,m(p,)減去式（3）得到的渦流損耗計算值cl(p,)，可以得一個頻率區間內不同峰值磁通密度對應的h+ex隨0.5的變化曲線[28]，有

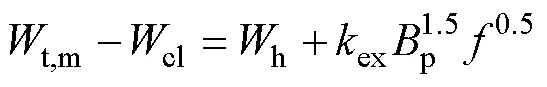
其中

式中，ex為剩余損耗擬合系數。

由式（21）可知，該曲線的節距對應于靜態磁滯損耗，0可以通過曲線的斜率得到。本文基于實驗測量的不同磁通密度下的低頻損耗（10Hz、50Hz、100Hz和150Hz），提取了超薄取向硅鋼片的靜態磁滯損耗h(p)和0(p)值，結果如圖6所示。

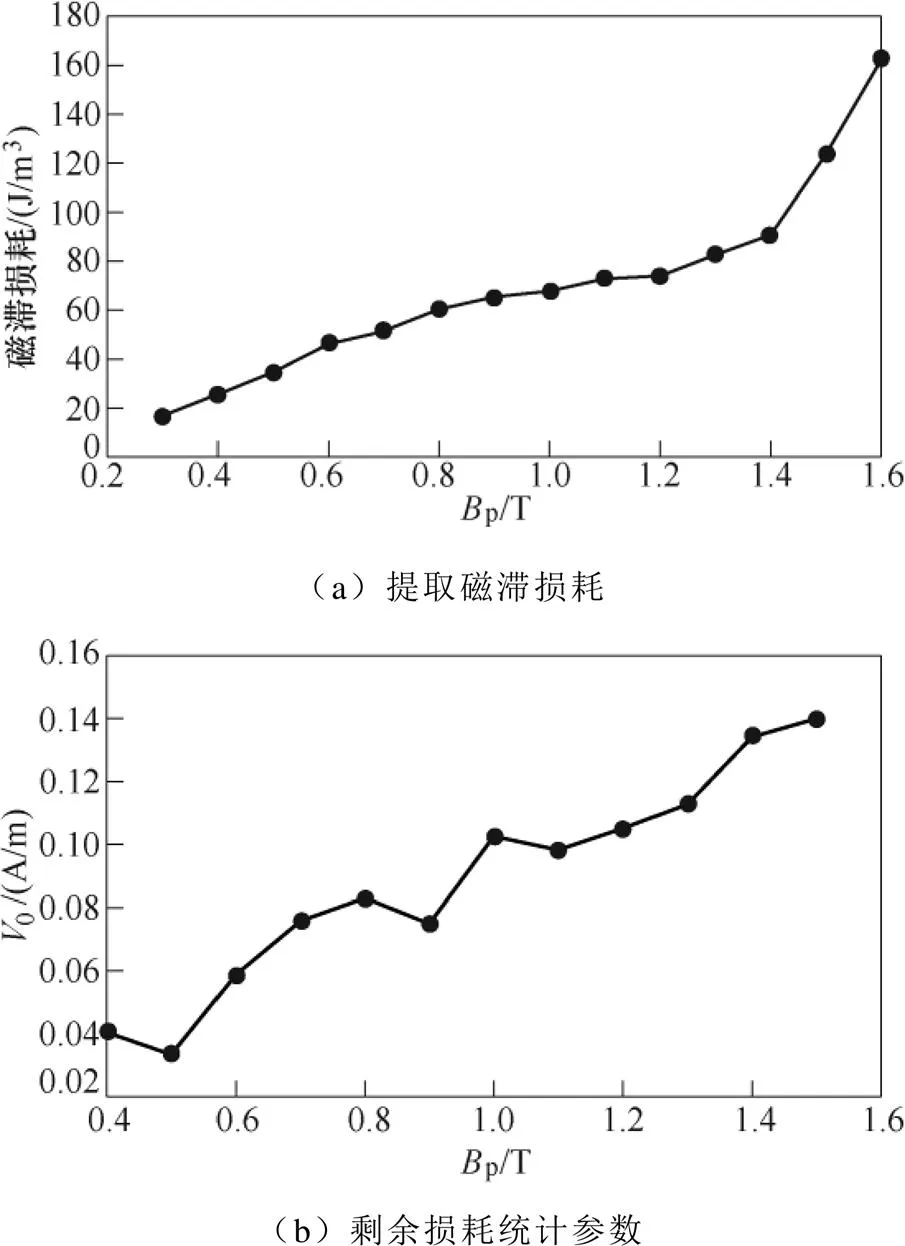
圖6 由測量值擬合獲得的Wh和V0隨Bp的變化曲線

基于不同磁通密度下的相對磁導率測量值，利用最小二乘法對式（7）進行擬合，得到超薄取向硅鋼片10Hz下（準靜態情況）相對磁導率隨峰值磁通密度變化曲線，如圖7所示。曲線系數1～6對應為11 014.86、-84 140.82、150 670.69、-105 271.87、60 410.24和-2 035.49。進一步將式（7）擬合曲線值代入式（8）可得到不同磁通密度的復數磁導率。

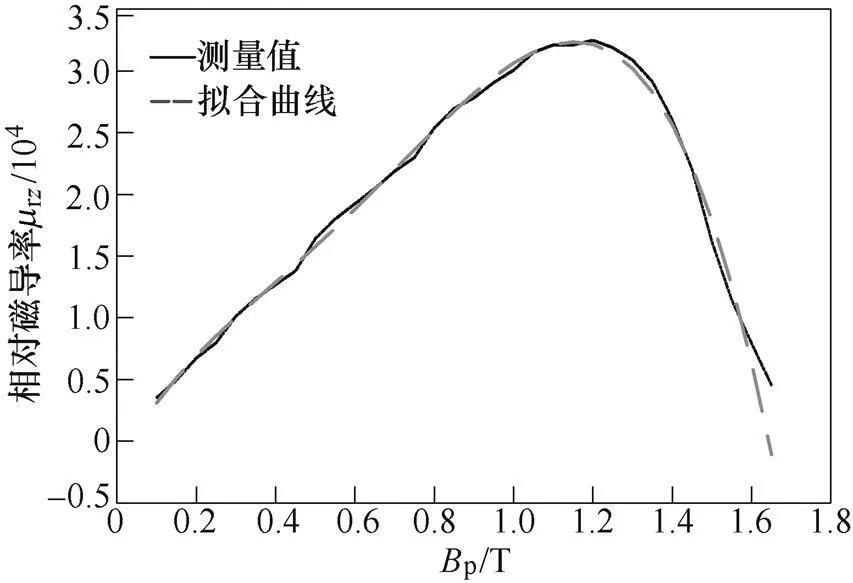
圖7 超薄取向硅鋼片10Hz相對磁導率隨磁通密度峰值變化

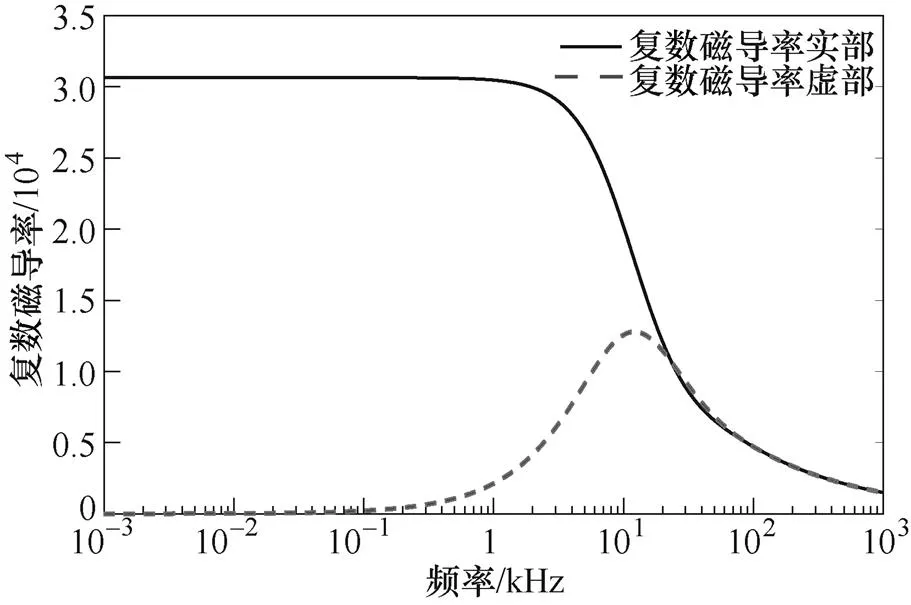
圖8 超薄取向硅鋼片1T下復數磁導率

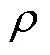
3.2 計算結果及誤差分析

本文將采用傳統STL模型（式（2）、式（3）、式（5）組成傳統STL模型）、基于線性磁化法則的改進損耗統計模型（式（2）、式（4）、式（5）組成模型一）、基于分數階導數的改進損耗統計模型（式（5）、式（10）、式（16）組成模型二），對10Hz～10kHz頻率范圍，0.4～1.5T磁通密度范圍內超薄取向硅鋼片的損耗進行計算，將上述三種模型的預測值與損耗測量值進行比較，結果如圖10～圖16所示。

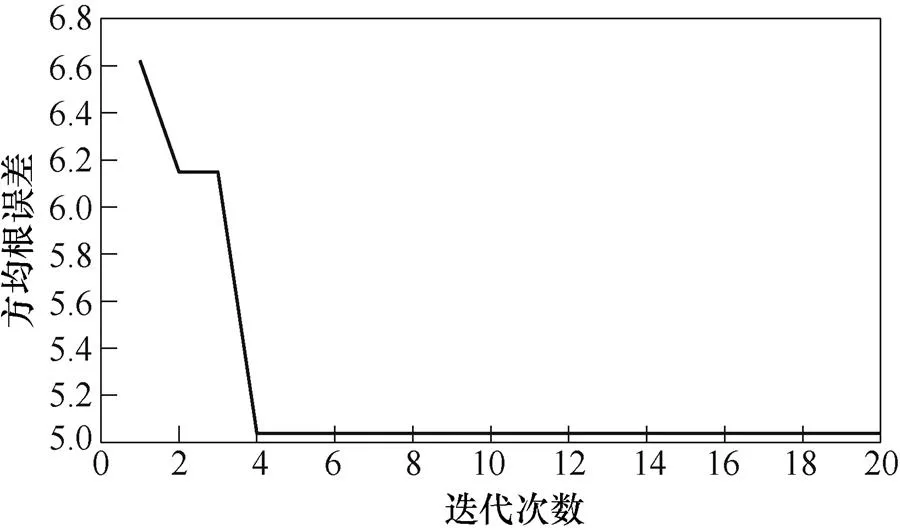
圖9 量子遺傳算法方均根誤差隨迭代次數變化

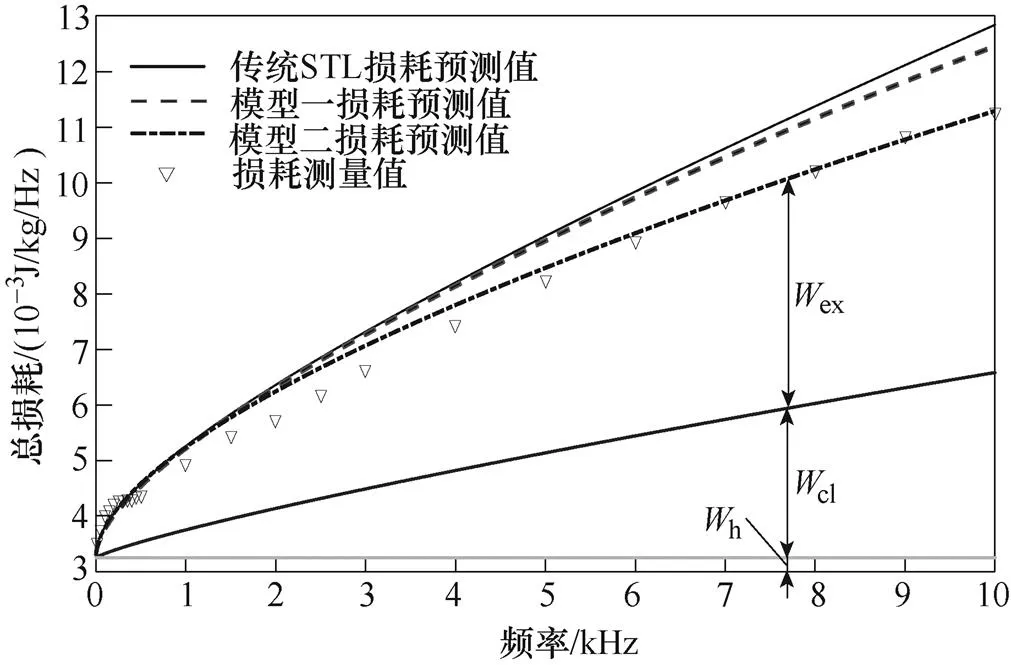
圖10 Bp=0.4T損耗預測與測量值對比

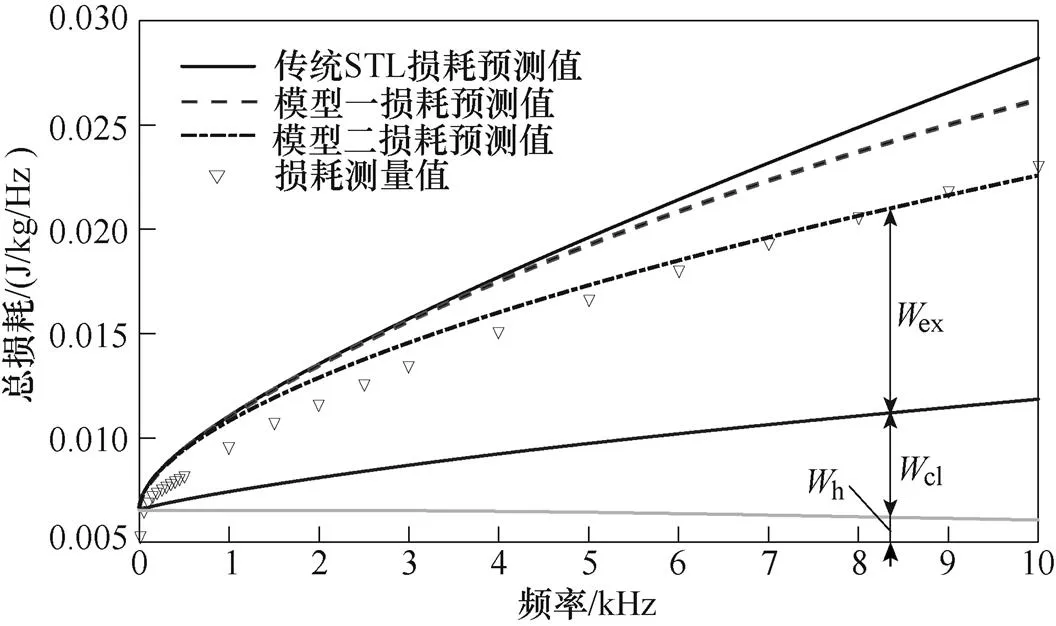
圖11 Bp=0.5T損耗預測與測量值對比

為了定量比較三種損耗計算模型的預測效果，本文引入平均相對誤差用于描述損耗計算模型的整體預測效果，平均相對誤差的表達式為

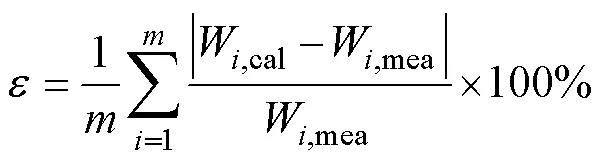
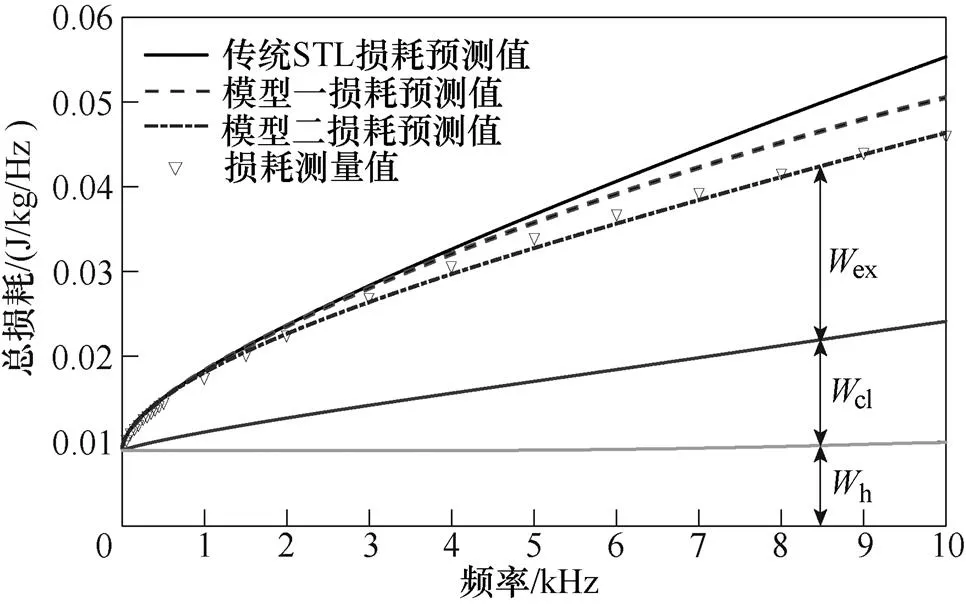
圖13 Bp=0.9T損耗預測與測量值對比

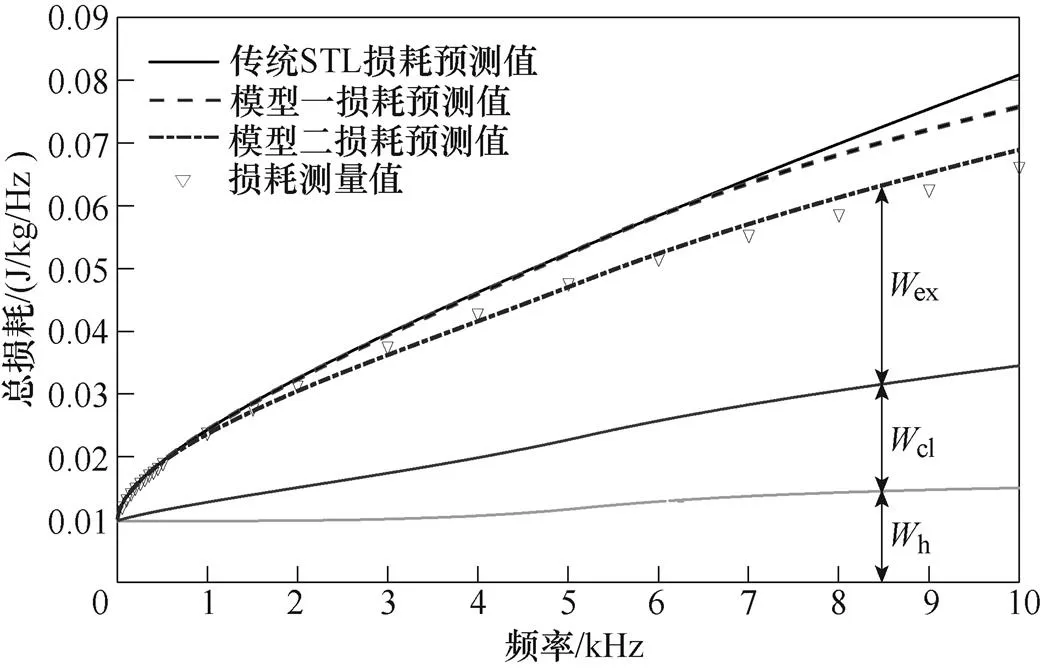
圖14 Bp=1.1T損耗預測與測量值對比

式中，為不同磁通密度下10Hz～10kHz范圍內的測量頻點數目，每個磁通密度下取22個測量頻點；W,cal為三類損耗計算模型不同磁通密度下計算值；W,mea為不同磁通密度實驗測量值。

表2對比了三種損耗計算模型在0.4～1.5T磁通密度范圍內的平均相對誤差。

三種損耗計算模型的平均相對誤差與峰值磁通密度變化曲線如圖17所示。可知，基于分數階的改進損耗統計模型（模型二）的平均相對誤差遠低于傳統STL和基于線性磁化準則的改進損耗統計模型（模型一），而模型一在低磁通密度下對損耗預測的精度較傳統STL有所改進，但在高磁通密度下預測精度的改善效果將不再明顯，這是由于線性磁化法僅適用于低磁通密度，這也進一步說明了模型一具有高磁通密度高頻損耗預測精度差的缺點，這與文獻[8-9]結論一致。

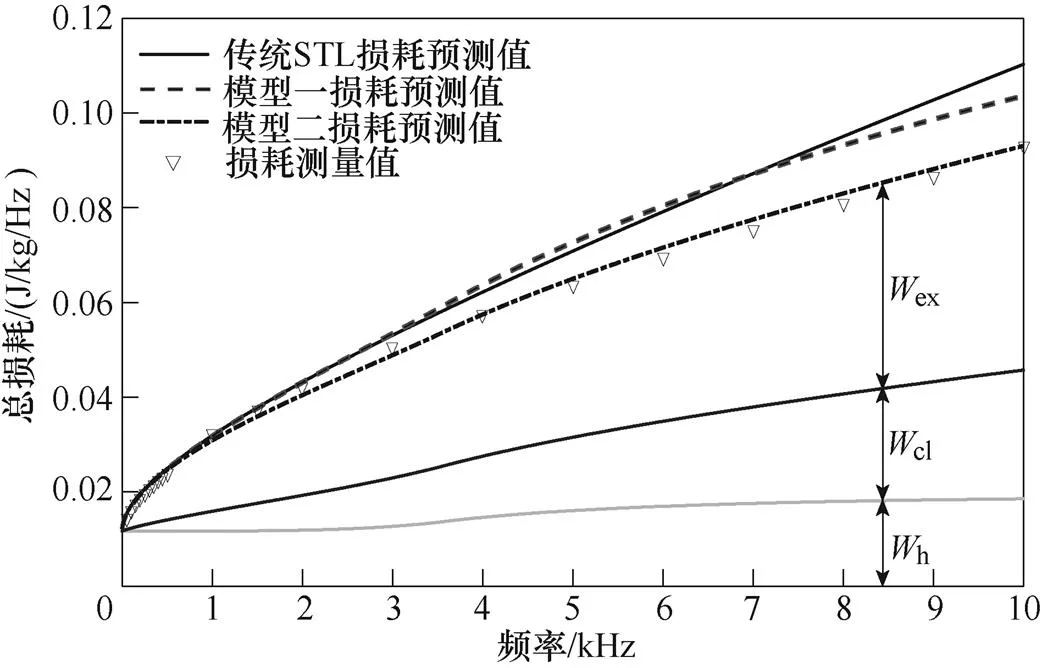
圖15 Bp=1.3T損耗預測與測量值對比

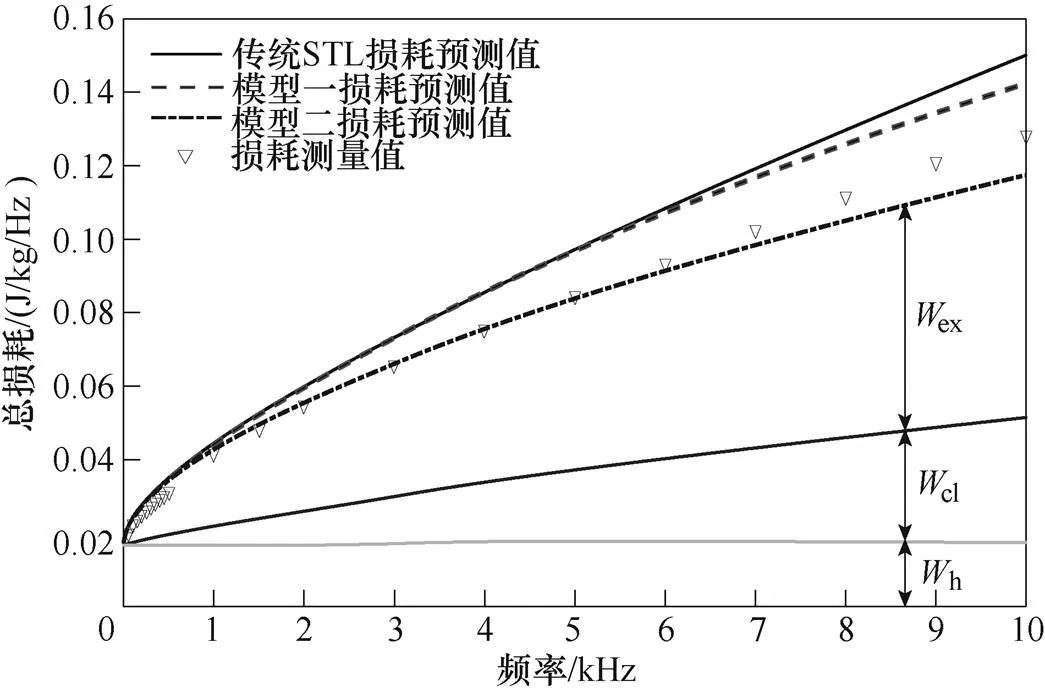
圖16 Bp=1.5T損耗預測與測量值對比

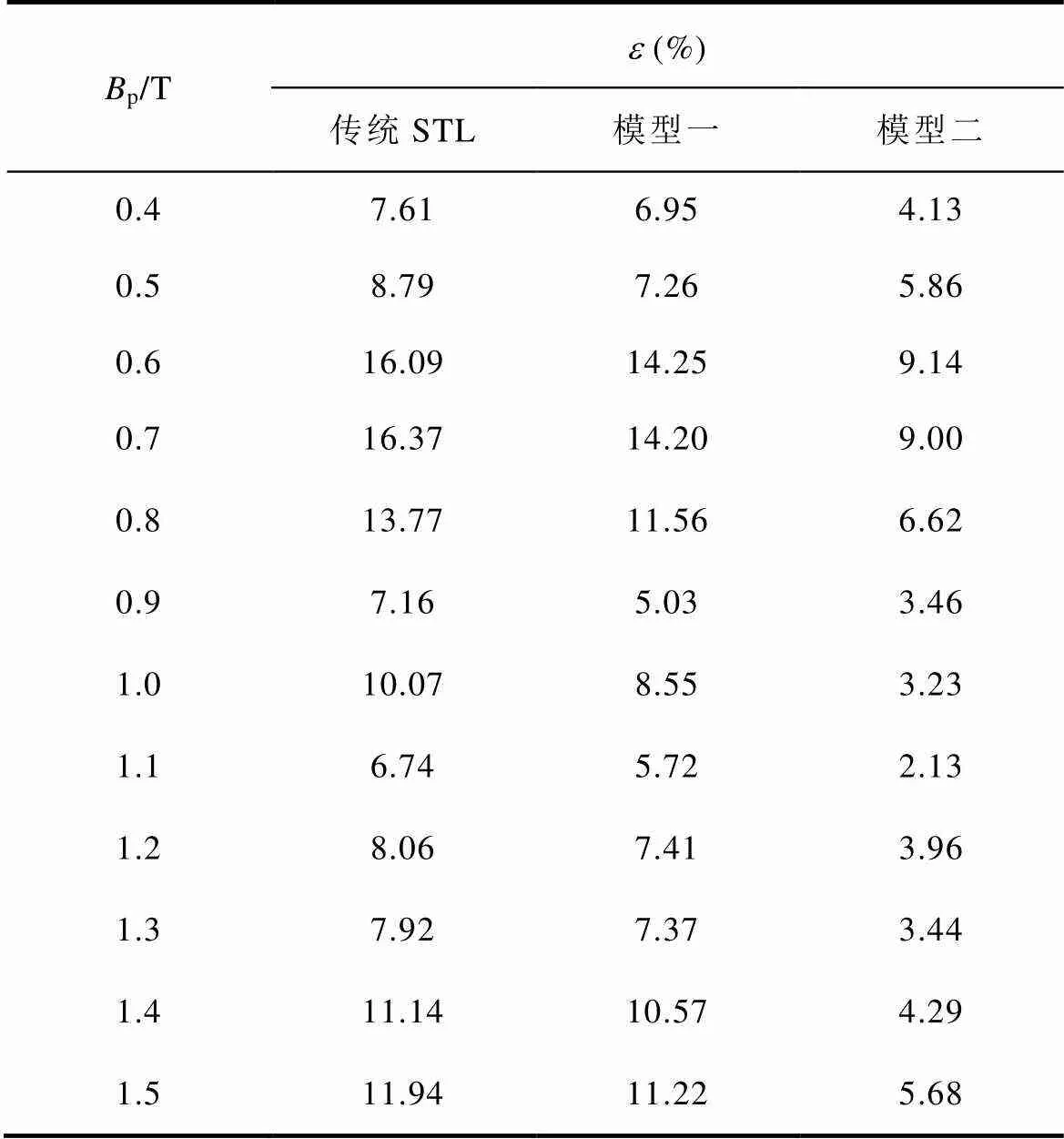
表2 三種損耗計算模型平均相對誤差e 對比

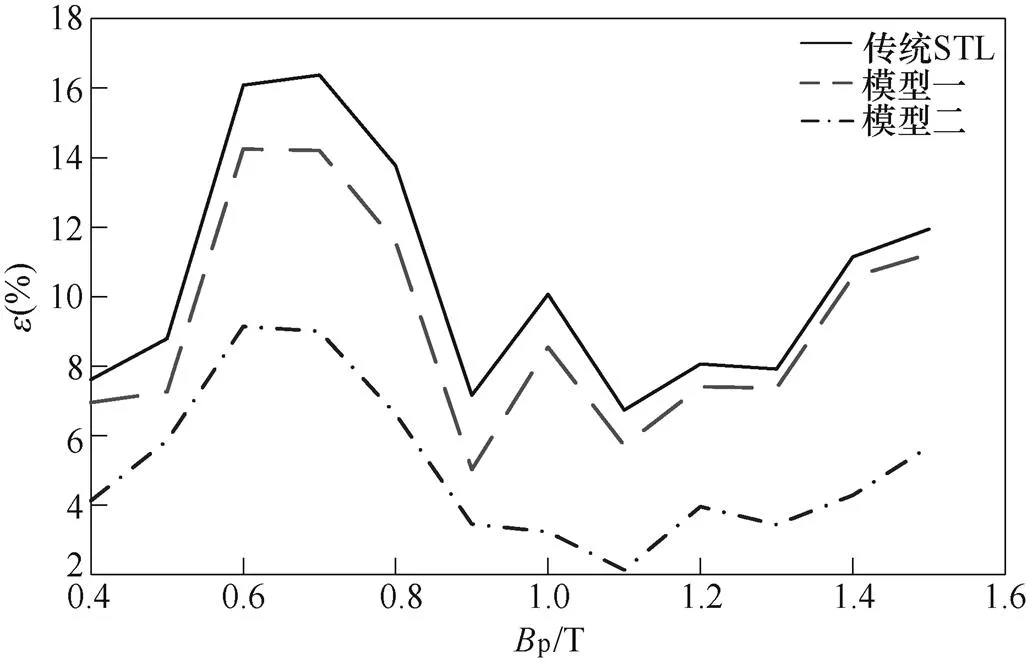
圖17 平均相對誤差隨峰值磁通密度變化曲線

4 結論

[1] 楊慶新, 李永建. 先進電工鐵磁材料特性與應用發展研究綜述[J]. 電工技術學報, 2016, 31(20): 1-11.

Yang Qingxin, Li Yongjian. Characteristics and developments of advanced magnetic materials in electrical engineering: a review[J]. Transactions of China Electrotechnical Society, 2016, 31(20): 1- 11.

[2] 劉任, 李琳, 王亞琦, 等. 基于隨機性與確定性混合優化算法的Jiles-Atherton磁滯模型參數提取[J]. 電工技術學報, 2019, 34(11): 2260-2268.

Liu Ren, Li Lin, Wang Yaqi, et al. Parameter extraction for Jiles-Atherton hysteresis model based on the hybrid technique of stochastic and deter- ministic optimization algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2260- 2268.

[3] Steinmetz C P. On the law of hysteresis[J]. Pro- ceedings of the IEEE, 1984, 72(2): 197-221.

[4] 劉剛, 孫立鵬, 王雪剛, 等. 正弦及諧波激勵下的鐵心損耗計算方法改進及仿真應用[J]. 電工技術學報, 2018, 33(21): 4909-4918.

Liu Gang, Sun Lipeng, Wang Xuegang, et al. Improvement of core loss calculation method and simulation application under sinusoidal and harmonic excitations[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4909-4918.

[5] Bertotti G. General properties of power losses in soft ferromagnetic materials[J]. IEEE Transactions on Magnetics, 1988, 24(1): 621-630.

[6] Kowal D, Sergeant P, Dupré L, et al. Comparison of iron loss models for electrical machines with different frequency domain and time domain methods for excess loss prediction[J]. IEEE Transactions on Magnetics, 2015, 51(1): 6300110.

[7] Zhao Hanyu, Ragusa C, Appino C, et al. Energy losses in soft magnetic materials under symmetric and asymmetric induction waveforms[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(3): 2655- 2665.

[8] Zhao Hanyu, Ragusa C, de la Barrière O, et al. Magnetic loss versus frequency in non-oriented steel sheets and its prediction: minor loops, PWM, and the limits of the analytical approach[J]. IEEE Transa- ctions on Magnetics, 2017, 53(11): 1-4.

[9] 段娜娜, 徐偉杰, 李永建, 等. 基于極限磁滯回線法的軟磁復合材料磁特性模擬[J]. 電工技術學報, 2018, 33(20): 4739-4745.

Duan Nana, Xu Weijie, Li Yongjian, et al. Electro- magnetic property modeling of the soft magnetic composite material based on the limiting loop method[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4739-4745.

[10] Zhang Yu, Pillay P, Ibrahim M, et al. Magnetic characteristics and core losses in machine laminations: high-frequency loss prediction from low-frequency measurements[J]. IEEE Transactions on Industry Applications, 2012, 48(2): 623-629.

[11] Steentjes S, Hameyer K, Dolinar D, et al. Iron-loss and magnetic hysteresis under arbitrary waveforms in NO electrical steel: a comparative study of hysteresis models[J]. IEEE Transactions on Industrial Elec- tronics, 2017, 64(3): 2511-2521.

[12] Raulet M A, Ducharne B, Masson J P, et al. The magnetic field diffusion equation including dynamic hysteresis: a linear formulation of the problem[J]. IEEE Transactions on Magnetics, 2004, 40(2): 872- 875.

[13] Ducharne B, Sebald G, Guyomar D, et al. Fractional model of magnetic field penetration into a toroidal soft ferromagnetic sample[J]. International Journal of Dynamics and Control, 2017, 6(1): 89-96.

[14] Guyomar D, Ducharne B, Sebald G, et al. Fractional derivative operators for modeling the dynamic polarization behavior as a function of frequency and electric field amplitude[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 2009, 56(3): 437-443.

[15] Zhang Bin, Gupta B, Ducharne B, et al. Dynamic magnetic scalar hysteresis lump model based on Jiles-Atherton quasi-static hysteresis model extended with dynamic fractional derivative contribution[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-5.

[16] Zhang Bin, Gupta B, Ducharne B, et al. Preisachs model extended with dynamic fractional derivation contribution[J]. IEEE Transactions on Magnetics, 2018, 54(3): 1-4.

[17] Ibrahim M, Pillay P. Advanced testing and modeling of magnetic materials including a new method of core loss separation for electrical machines[J]. IEEE Transactions on Industry Applications, 2012, 48(5): 1507-1515.

[18] Mthombeni T L, Pillay P. Physical basis for the variation of lamination core loss coefficients as a function of frequency and flux density[C]//IECON 2006-32nd Annual Conference on IEEE Industrial Electronics, Paris, 2006: 1381-1387.

[19] Hamzehbahmani H, Anderson P, Hall J, et al. Eddy current loss estimation of edge burr-affected magnetic laminations based on equivalent electrical network- part II: analytical modeling and experimental results[J]. IEEE Transactions on Power Delivery, 2014, 29(2): 651-659.

[20] 陳文, 孫洪廣, 李西成. 力學與工程問題的分數階導數建模[M]. 北京: 科學出版社, 2010.

[21] 吳強, 黃建華. 分數階微積分[M]. 北京: 清華大學出版社, 2016.

[22] Chandrasena W, McLaren P G, Annakkage U D, et al. An improved low-frequency transformer model for use in GIC studies[J]. IEEE Transactions on Power Delivery, 2004, 19(2): 643-651.

[23] Zhang Bin, Ducharne B, Sebald G, et al. Characteri- zation of fractional order for high-frequency band- width model of dielectric ferroelectrics[J]. Journal of Intelligent Material Systems and Structures, 2014, 27(4): 437-443.

[24] Ducharne B, Sebald G, Guyomar D, et al. Dynamics of magnetic field penetration into soft ferromagnets[J]. Journal of Applied Physics, 2005, 117(24): 243907.

[25] 蘇玉剛, 吳學穎, 趙魚名, 等. 互補對稱式LCC諧振網絡的電場耦合式無線電能傳輸系統參數優化[J]. 電工技術學報, 2019, 34(14): 2874-2883.

Su Yugang, Wu Xueying, Zhao Yuming, et al. Parameter optimization of electric-field coupled wireless power transfer system with complementary symmetric LCC resonant network[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 2874- 2883.

[26] 馬書民, 戎子睿, 林湘寧, 等. 計及多類裝置協同的直流偏磁治理設備全局優化配置研究[J]. 中國電機工程學報, 2020, 40(14): 4387-4399, 4720.

Ma Shumin, Rong Zirui, Lin Xiangning, et al. Study on the global optimal configuration of DC bias equipment considering the cooperation of multiple devices[J]. Proceedings of the CSEE, 2020, 40(14): 4387-4399, 4720.

[27] 趙小軍, 劉小娜, 肖帆, 等. 基于Preisach模型的取向硅鋼片直流偏磁磁滯及損耗特性模擬[J]. 電工技術學報, 2020, 35(9): 1849-1857.

Zhao Xiaojun, Liu Xiaona, Xiao Fan, et al. Hysteretic and loss modeling of silicon steel sheet under the DC biased magnetization based on the Preisach model[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1849-1857.

[28] Barbisio E, Fiorillo F, Ragusa C. Predicting loss in magnetic steels under arbitrary induction waveform and with minor hysteresis loops[J]. IEEE Transa- ctions on Magnetics, 2004, 40(4): 1810-1819.

[29] Liu Ren, Li Lin. Analytical prediction model of energy losses in soft magnetic materials over broad- band frequency range[J]. IEEE Transactions on Power Electronics, 2020, 36(2): 2009-2017.

Calculation Method of High-Frequency Loss of Ferromagnetic Materials Based on R-L Type Fractional Derivative and Loss Statistical Theory

1,221,31,2

（1. Hubei Provincial Engineering Technology Research Center for Power Transmission Line Yichang 443002 China 2. College of Electrical Engineering and New Energy China Three Gorges University Yichang 443002 China 3. Yichang Electric Company State Grid Hubei Electric Power Company Yichang 443002 China）

The traditional statistical theory of loss (STL) has a large prediction error of high-frequency loss of ferromagnetic materials and the estimation is too high. For this reason, this paper firstly considers the influence of the uneven distribution of magnetic flux density on hysteresis loss under high-frequency conditions, and proposes a calculation method for hysteresis loss based on the finite element method. Then based on the R-L type fractional derivative, the eddy current field and eddy current loss calculation formulae in the traditional STL are improved, and the quantum genetic algorithm is introduced to optimize the damping coefficient and the order of the derivative in the fractional derivative model. Subsequently, an improved STL method suitable for wide frequency and wide magnetic density range is proposed. Finally, the Epstein frame is used to measure the loss of 3% Si-Fe ultra-thin oriented silicon steel sheet in the frequency range of 10Hz to 10kHz. Comparing the theoretical calculation value with the experimental measurement value, the result shows that the maximum average relative error of the proposed method in the entire frequency band is 9.14%, the minimum average relative error is 2.13%. Compared with the traditional loss theory, the loss prediction accuracy is greatly improved, which verifies the effectiveness of this method.

Loss statistical theory, hysteresis loss, eddy current loss, fractional derivative, quantum genetic algorithm

TM153; TM275

10.19595/j.cnki.1000-6753.tces.201462

國家自然科學基金青年科學基金項目（52107006）和湖北省自然科學基金面上項目（2021CFB149）資助。

2020-11-01

2020-12-06

陳 彬 男，1989年生，博士，研究生導師，研究方向為電力裝備電磁特性模擬與測量技術、新型電工磁性材料綜合磁特性模擬與測量技術。

E-mail: chenbin@ctgu.edu.cn（通信作者）

秦小彬 男，1994年生，碩士研究生，研究方向為新型磁性材料損耗與磁滯特性模擬。

E-mail: 2902915609@qq.com

（編輯 崔文靜）