基于虛擬電壓注入的閉環磁鏈觀測器的感應電機無速度傳感器矢量控制系統

王震宇 孫 偉 蔣 棟

基于虛擬電壓注入的閉環磁鏈觀測器的感應電機無速度傳感器矢量控制系統

王震宇 孫 偉 蔣 棟

（華中科技大學電氣與電子工程學院 武漢 430074）

多年來，感應電機無速度傳感器矢量控制系統在低同步轉速區域的不穩定問題一直沒有得到解決。該不穩定問題由系統狀態變量不能觀、極點分布不穩定以及電機參數魯棒性弱共同導致。當且僅當三個問題被同時解決時，低同步轉速區域的不穩定問題才能夠得到解決。該文以經典的閉環磁鏈觀測器為基礎，采用虛擬電壓注入法改進其低速穩定性。與傳統高頻/低頻信號注入法不同，虛擬電壓注入法不在電機中注入信號，而是在觀測器中注入虛擬電壓。虛擬電壓注入能同時解決系統狀態變量能觀性、極點分布穩定性和電機參數魯棒性問題，最終實現系統在低同步轉速區域的穩定運行。

感應電機 無速度傳感器 閉環磁鏈觀測器 虛擬電壓注入

0 引言

近年來，感應電機無速度傳感器矢量控制系統，因其成本低、可靠性高、維護簡易等優勢，成為國內外電氣傳動領域研究的焦點，在工業上得到廣泛應用。但低速區域下，尤其是接近零同步轉速時，系統的不穩定問題限制了驅動系統的運行范圍以及應用場合。針對這一問題，國內外學者們提出了許多改進方法。這些方法一般可以分為兩類。

（1）基于電機各向異性的信號提取法。這類方法利用轉子齒槽諧波、互感的飽和特性、人造凸極性或轉子漏抗，通過向電機注入信號，提取轉子轉速和位置信息[1]。文獻[2]基于高頻信號注入法，利用同步濾波器提取轉子位置信息。同時提出了一種新型的擾動辨識方法，無需離線預處理，實現轉子轉速在線辨識。文獻[3]引入額外的電流傳感器測量感應電機零序電流，通過零序電流的變化反映電機漏感的變化，并提取出轉子位置信息，估計電機轉速。文獻[4]基于脈振電壓注入法，提出新型的信號分離方法，獲取精確的齒槽凸極性信息，從而可以獲得精確的轉子轉速。通過上述信號提取法，無速度傳感器矢量控制系統可以在低速甚至零同步轉速下穩定長時間運行。但感應電機各向異性較弱，難以通過簡易高效的方法提取轉子轉速和磁鏈定向信息。因此，信號提取法不適用于工業應用（但這種方法在永磁電機[5-8]和同步磁阻電機[9]的無速度傳感器系統中很常見）。

（2）基于感應電機基波數學模型的基波模型法。相較于信號提取法，基波模型法通用性強，在工業中應用廣泛。文獻[10]改進了傳統全階磁鏈觀測器，自適應地調整反饋矩陣系數，提高了低速發電模式下，系統的穩定性和轉速估計精度。基于傳統的轉子磁鏈誤差模型參考自適應系統（Model Reference Adaptive System, MRAS），文獻[11]提出了一種自適應線性神經元速度觀測器，利用神經網絡自適應修改轉速自適應律權重系數，保證了系統的低速起動穩定性。文獻[12]提出了一種基于感應電機反電動勢的高階滑模觀測器，提高了觀測器的參數魯棒性，同時削弱了系統抖振。文獻[13]提出了一種基于改進指數趨近律的滑模觀測器，進一步削弱了系統抖振，并實現了對系統狀態的自適應控制。文獻[14]基于對稱強跟蹤擴展卡爾曼濾波器進行轉子轉速辨識，提高了轉速估計精度和跟蹤速度，并對噪聲進行抑制。文獻[15]在傳統的轉子磁鏈誤差MRAS的基礎上，提出了閉環磁鏈觀測器（Closed-Loop Flux Observer, CLFO），解決了電壓模型的純積分問題，改善了系統的低速性能，但仍然存在低速運行不穩定問題。通過上述基波模型法，無速度傳感器驅動系統在低速下的性能得到極大改善，不穩定區域減小，但是不穩定問題仍然存在。

本文對基于CLFO的感應電機無速度傳感器矢量控制系統的低速不穩定問題進行了研究。分別利用非線性系統局部弱能觀性理論[16]分析狀態變量的能觀性、利用小信號擾動理論分析矢量控制系統的極點穩定性和參數魯棒性，得到了導致CLFO低速不穩定問題的原因。針對不穩定現象提出了虛擬電壓注入法，能夠同時解決轉速能觀性、系統極點穩定性和電機參數魯棒性問題，進而實現CLFO系統在低速區域的穩定運行。

1 傳統閉環觀測器低同步轉速區域的不穩定問題

1.1 閉環磁鏈觀測器

在dq兩相旋轉坐標系下，閉環磁鏈觀測器數學模型為

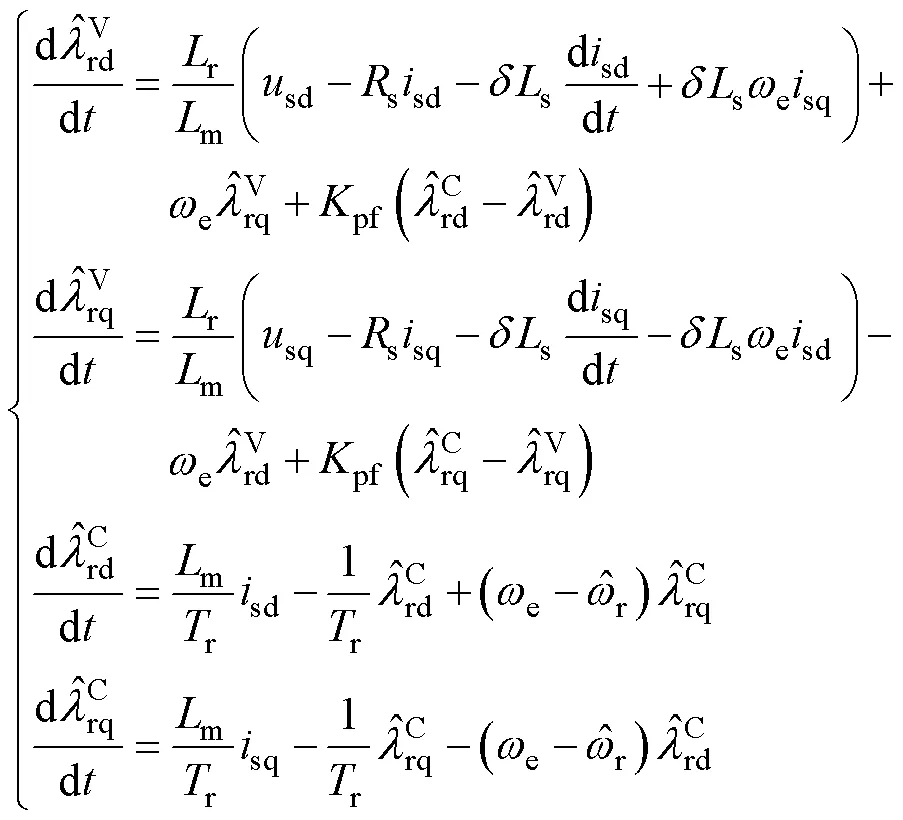
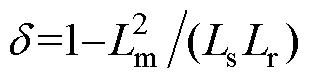
轉速觀測器自適應律為

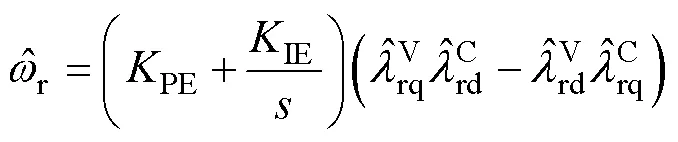
式中，PE與IE分別為轉速自適應律PI參數。

基于電機基波模型構建的觀測器，均具有低同步轉速區域的不穩定問題[17]。該問題由轉速能觀性、系統極點穩定性和電機參數魯棒性問題共同導致。

基于CLFO構建的感應電機無速度傳感器矢量控制系統同樣具有低同步轉速區域的不穩定問題[15]，本文將分別對CLFO系統的轉速能觀性、系統極點穩定性以及對電機參數魯棒性進行分析，從而歸納出低速不穩定問題的原因。

1.2 非線性系統的局部弱能觀性

本文將利用非線性系統的局部弱能觀理論[16]對觀測器的能觀性進行分析。非線性系統的局部弱能觀理論描述如下。

假定一個非線性動態系統為

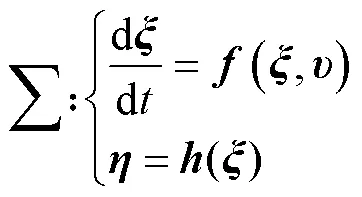
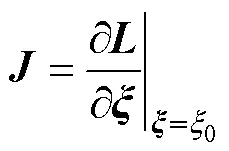
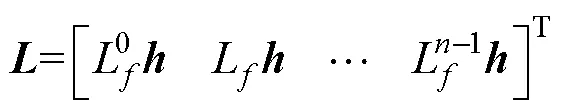
如果矩陣滿秩，即

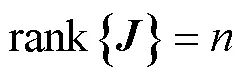
根據非線性系統的局部弱能性理論和式（1），得到基于CLFO的非線性動態系統為

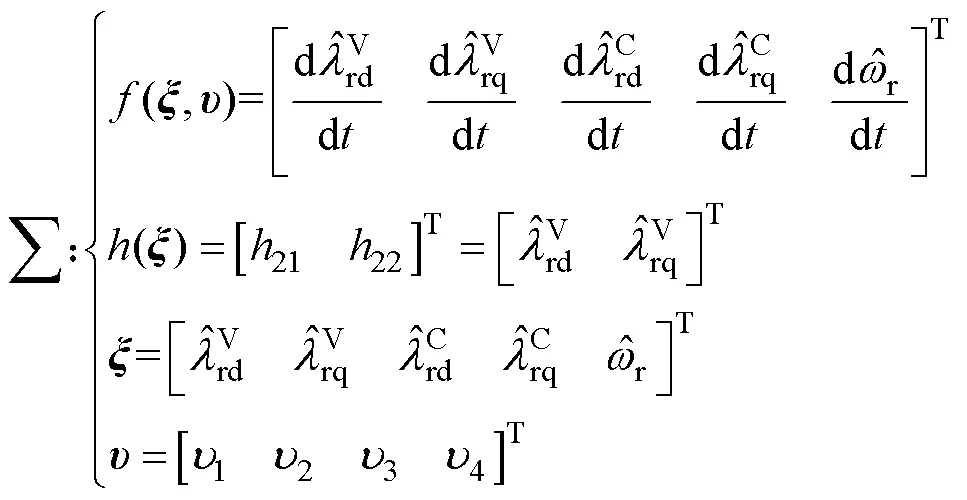
其中

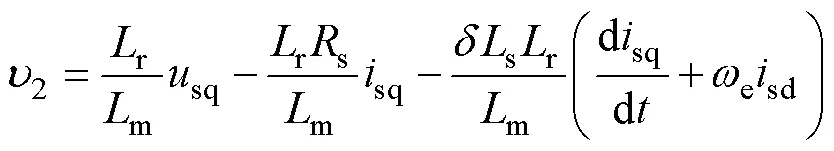
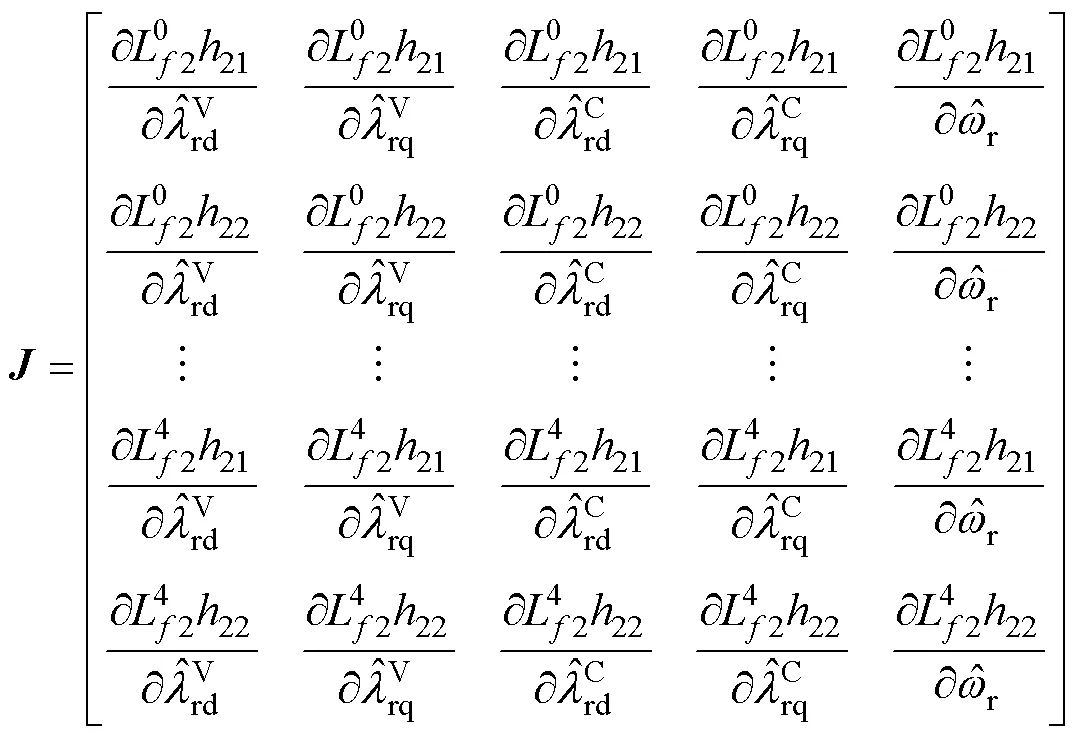
式（8）為10×5矩陣。根據局部弱能觀性理論[16]，當且僅當滿秩時，系統中的狀態變量具有局部弱能觀性。因此提取式（8）中前四行與第六行，得到矩陣1為

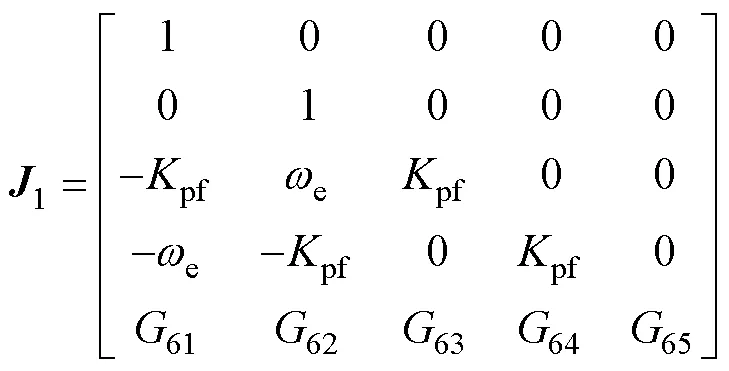
其中

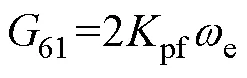
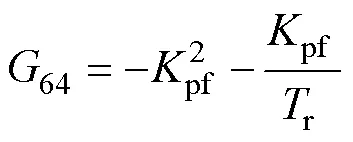
由式（9）得1的行列式1為

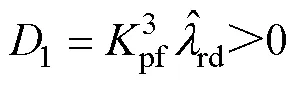
即矩陣1的秩為5，因此矩陣滿秩。根據局部弱能觀性理論可知：基于CLFO構建的非線性系統中的狀態變量在所有轉速區域（包括e0rad/s時），均具有局部弱能觀性。

1.3 無速度傳感器矢量控制系統極點穩定性

傳統CLFO系統的傳遞函數框圖如圖1所示。圖中，e為感應電機電磁轉矩，L為負載轉矩，為轉子轉動慣量，為轉子摩擦因數。

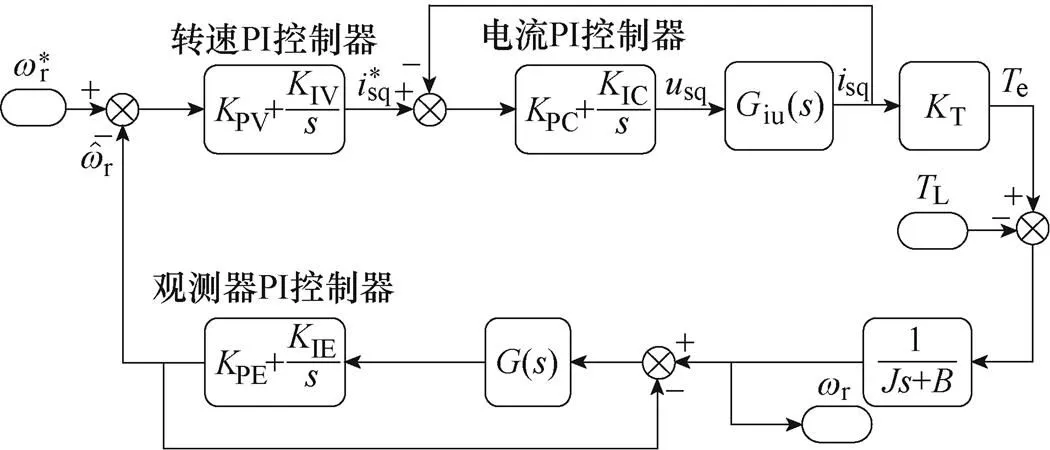
圖1 傳統CLFO系統的傳遞函數框圖

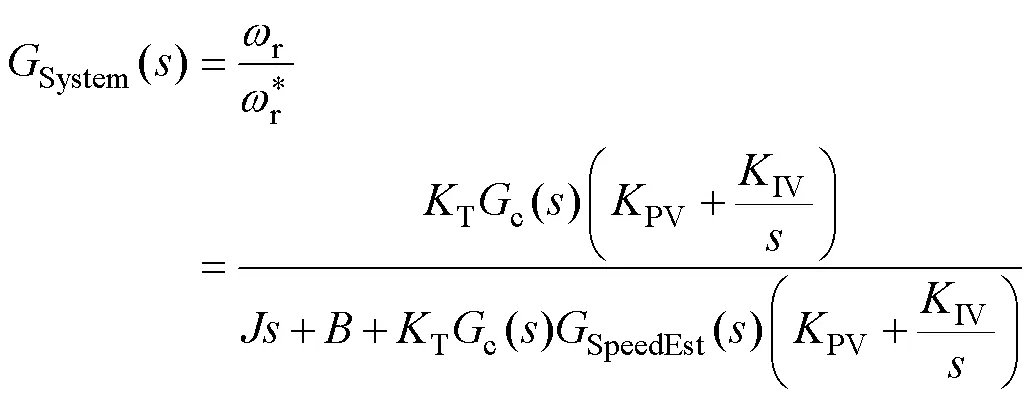
其中

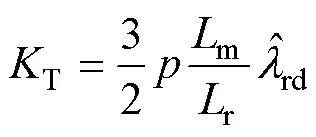
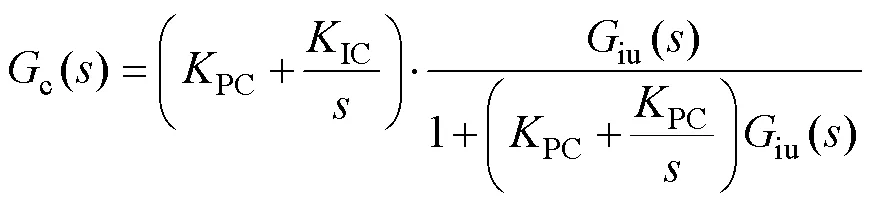
式中，PV與IV分別為轉速PI控制器PI參數；PC與IC分別為電流PI控制器PI參數；為電機極 對數。

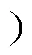
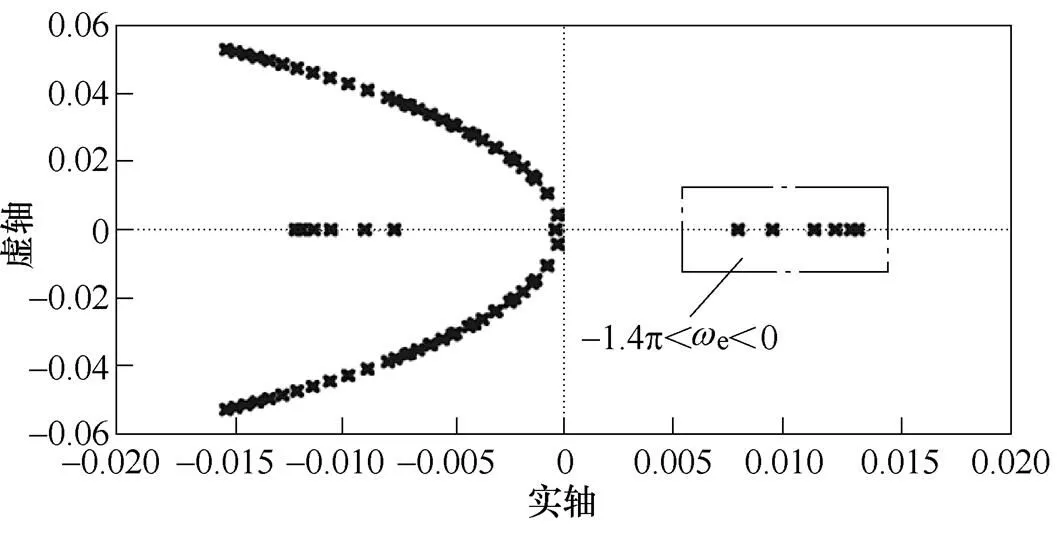
圖2 傳統CLFO系統的極點分布

1.4 對電機參數變化的魯棒性

根據式（11）可以得到電機參數（定子電阻、轉子電阻、互感）變化時的轉子實際轉速與參考轉速的傳遞函數為

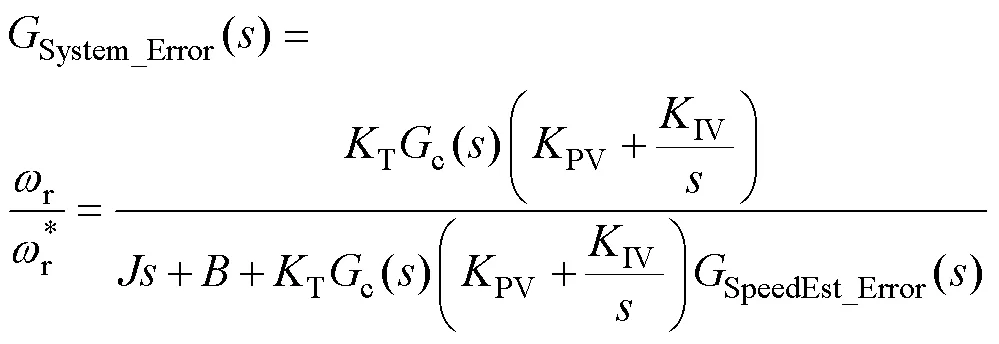
其中

根據式（12）可以得到，當電機參數發生變化時，傳統CLFO系統的極點分布，如圖3所示。

由圖3可知，當電機參數不準確時，系統閉環傳遞函數在低同步轉速區間存在右半平面極點，系統參數魯棒性弱，系統不能穩定運行。在實際工業應用中，電機參數很難精確獲得，并且電機參數隨著電機運行時間的增加會發生漂移。系統參數魯棒性弱，也是導致系統低速不穩定問題的原因之一。

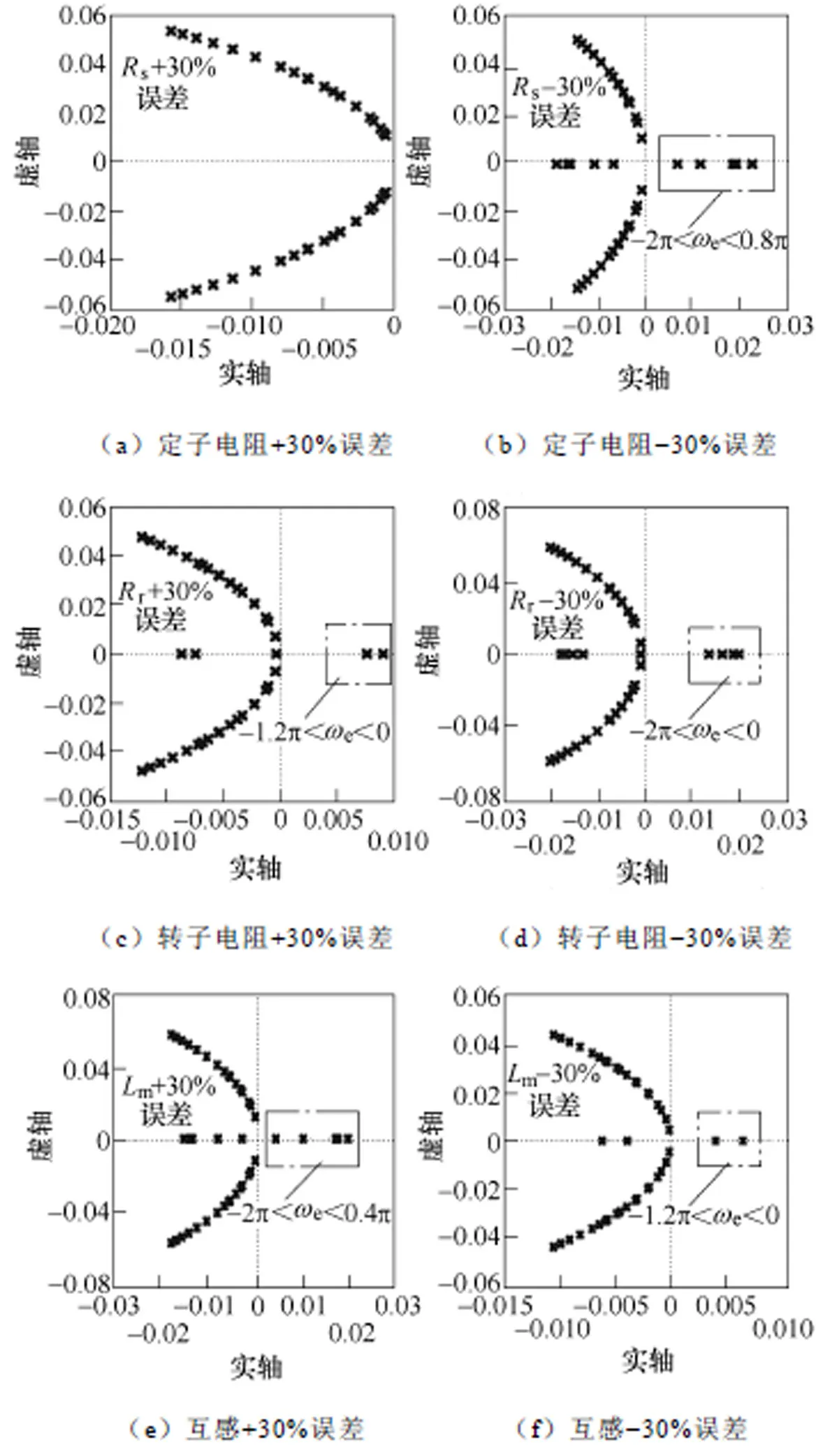
圖3 電機參數變化時，傳統CLFO系統的極點分布

綜上所述，雖然CLFO中的狀態變量在任何轉速區間均具有局部弱能觀性，但由于系統極點不穩定且參數魯棒性弱，基于CLFO構建的無速度傳感器矢量控制系統存在低速不穩定問題。

2 虛擬電壓注入法

由于感應電機的各向異性很弱，利用傳統的高頻或低頻信號注入法很難提取有效的位置或轉速信息，因此傳統信號注入法很少應用在感應電機中。與傳統信號注入法相比，虛擬電壓注入法僅在觀測器中注入額外的電壓信號（不需要在電機中注入），就能夠同時解決系統極點不穩定問題和對電機參數魯棒性問題，并且能夠提升閉環觀測器中狀態變量的觀測度（即量化了的能觀性），進而解決傳統的CLFO系統的不穩定問題。

基于虛擬電壓注入的CLFO系統結構框圖如圖4所示。

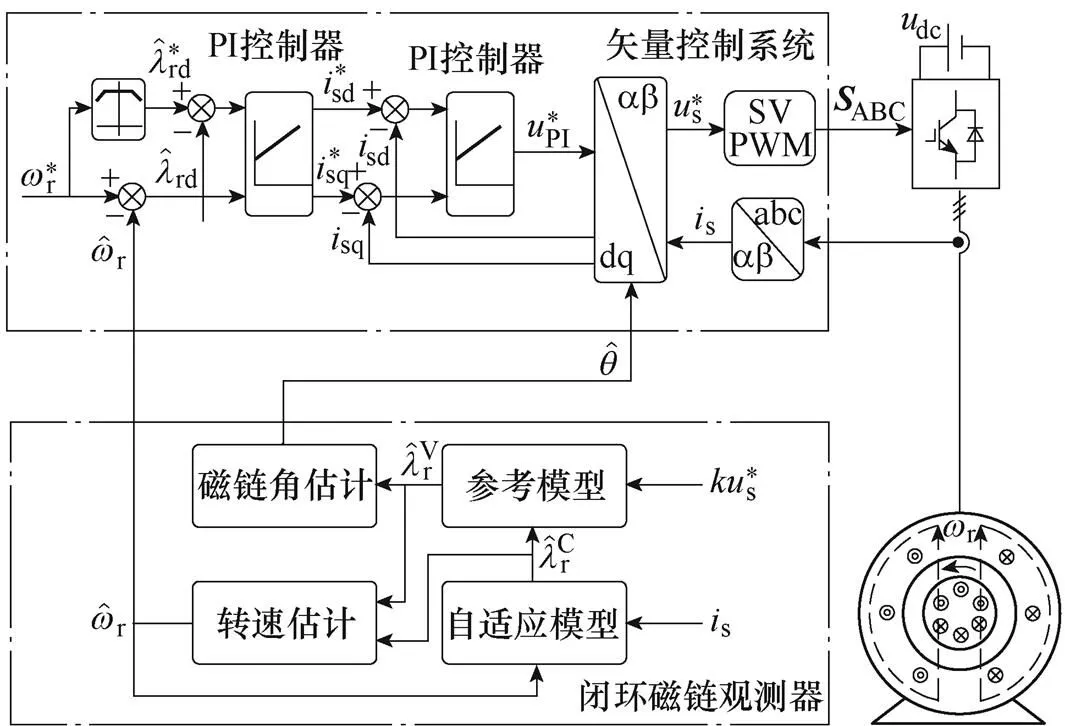
圖4 基于虛擬電壓注入的CLFO系統結構框圖

觀測器數學模型為

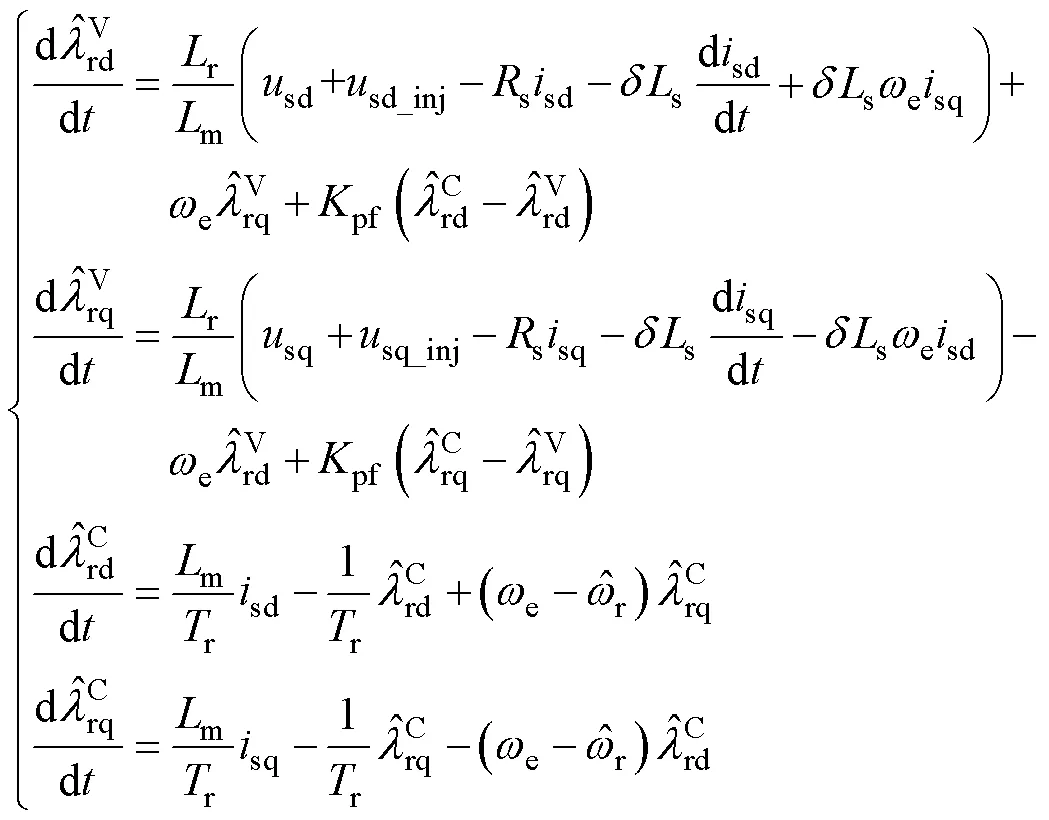
2.1 虛擬電壓注入法對系統能觀性的改進

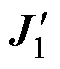
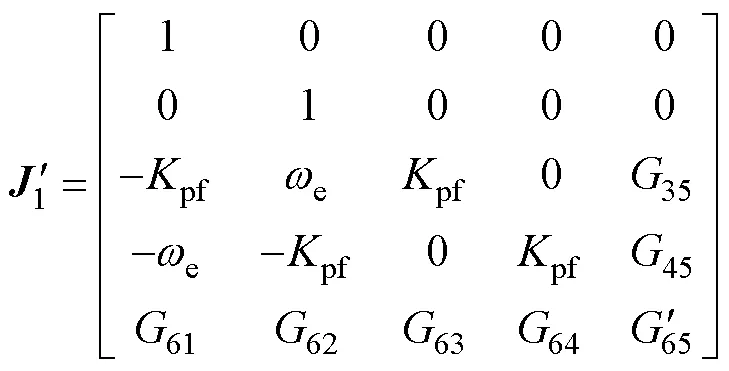
其中

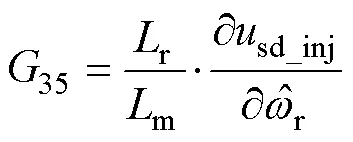
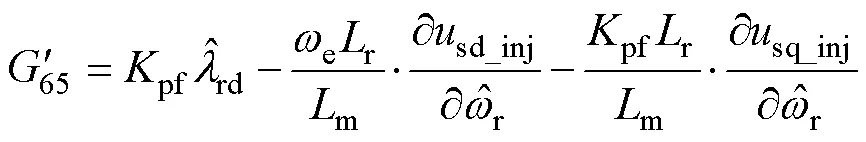
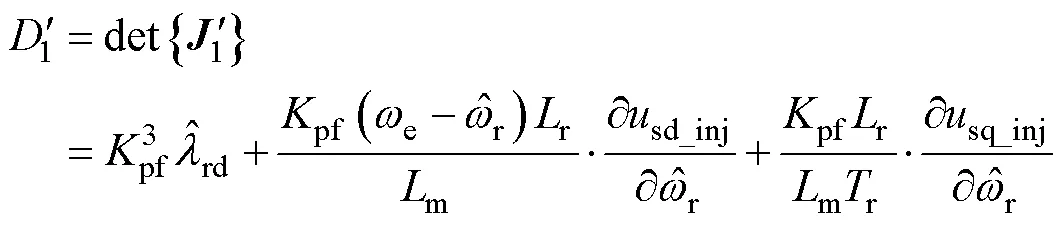
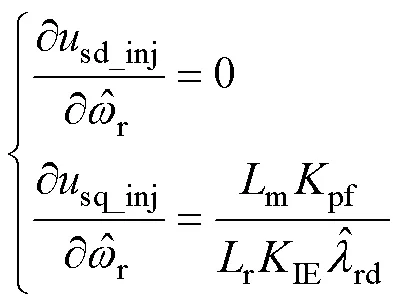
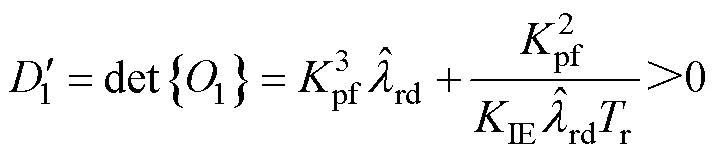
雖然虛擬電壓注入前后，CLFO的狀態變量均具有局部弱能觀性，但引入虛擬電壓后，觀測器的能觀度（能觀性的定量描述）增強了。

本文將文獻[18]中的能觀性結論進行了擴展，得到系統能觀性的定量化描述。且當

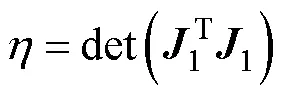
越大時，系統能觀度越大，系統穩定區域越大，觀測器抗干擾能力越強[18]。

未注入虛擬電壓的CLFO能觀度如式（18）所示，注入虛擬電壓后，CLFO能觀度為

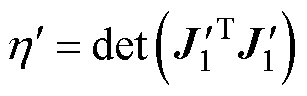
根據式（10）和式（17）可得

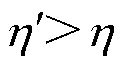
因此，當注入虛擬電壓后，系統的能觀度增大，系統在零同步轉速下的局部弱能觀性得到增強。

2.2 虛擬電壓注入法對系統低頻穩定性的改進

引入虛擬電壓注入時，CLFO系統的傳遞函數框圖如圖5所示。

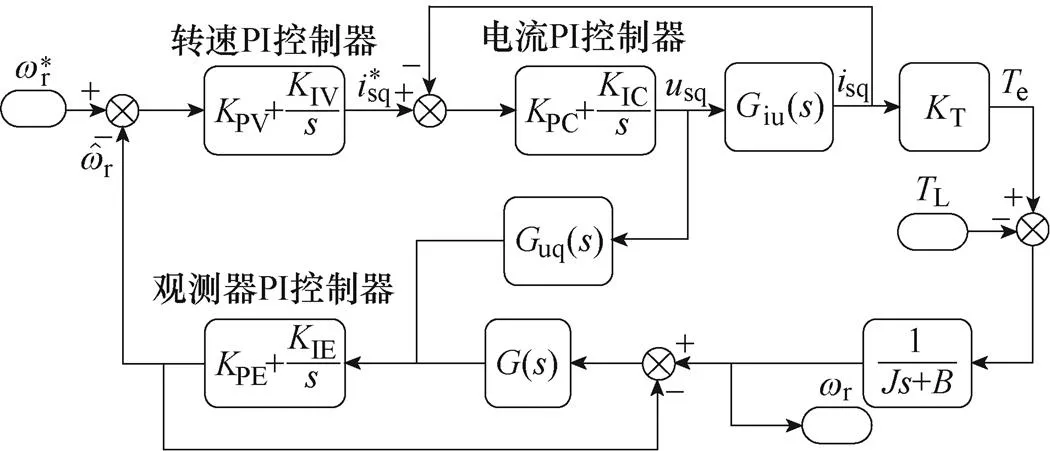
圖5 基于虛擬電壓注入的CLFO系統的傳遞函數框圖

由圖5可得引入虛擬電壓注入時轉子實際轉速與參考轉速的傳遞函數為

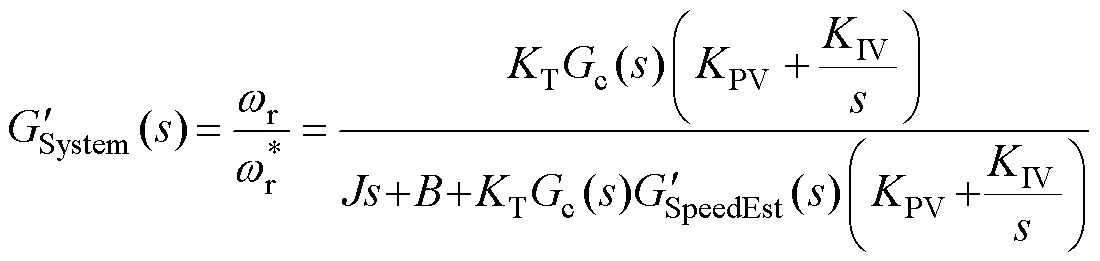
其中

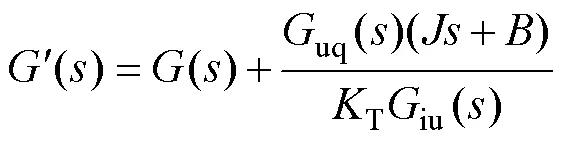
根據式（21）可以得到基于虛擬電壓注入的CLFO系統的閉環傳遞函數極點分布，如圖6所示。圖中，注入系數=1.5，相比圖2中的極點分布，在圖6中系統不存在右半平面極點，極點不穩定問題得到解決。

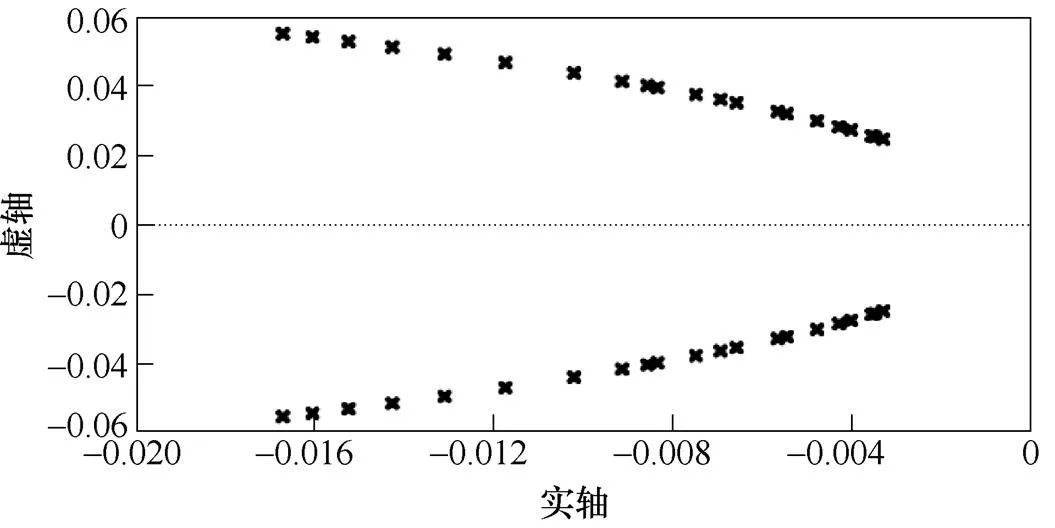
圖6 基于虛擬電壓注入的CLFO系統的極點分布，k=1.5

2.3 虛擬電壓注入法對系統魯棒性的改進

引入虛擬電壓后，同樣地，根據式（21）可以得到電機參數（定子電阻、轉子電阻、互感）變化時的轉子實際轉速與參考轉速的傳遞函數為

其中

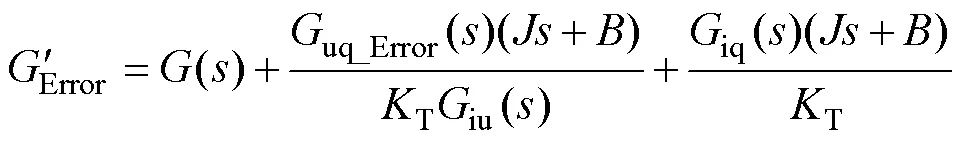
根據式（22）可以得到，當電機參數變化時，系統的閉環傳遞函數極點分布，如圖7所示。注入系數=1.5。相比圖3中的極點分布，系統在低同步轉速下，不存在不穩定極點，系統始終保持穩定。

通過以上分析可知，基于CLFO的無速度傳感器矢量控制系統在低同步轉速下的不穩定問題，可通過虛擬電壓注入解決。虛擬電壓注入對CLFO系統的性能改進見表1。

虛擬電壓注入增強了系統的轉速能觀性，解決了低速下系統極點的不穩定問題與對電機參數變化的魯棒性弱的問題，進而實現了系統在低同步轉速下（包括零同步轉速）的穩定運行。

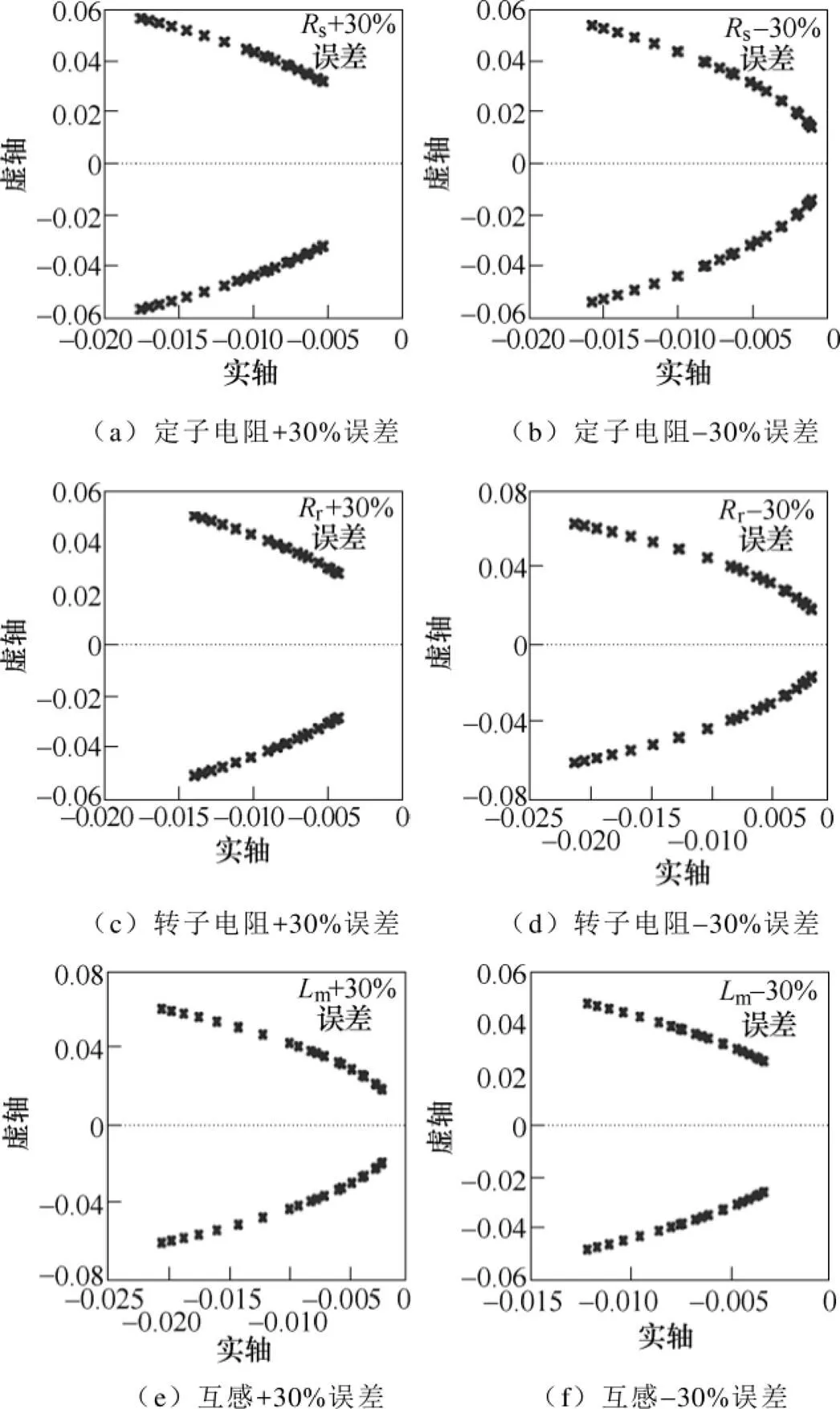
圖7 電機參數變化時，基于虛擬電壓注入的 CLFO系統的極點分布，k=1.5

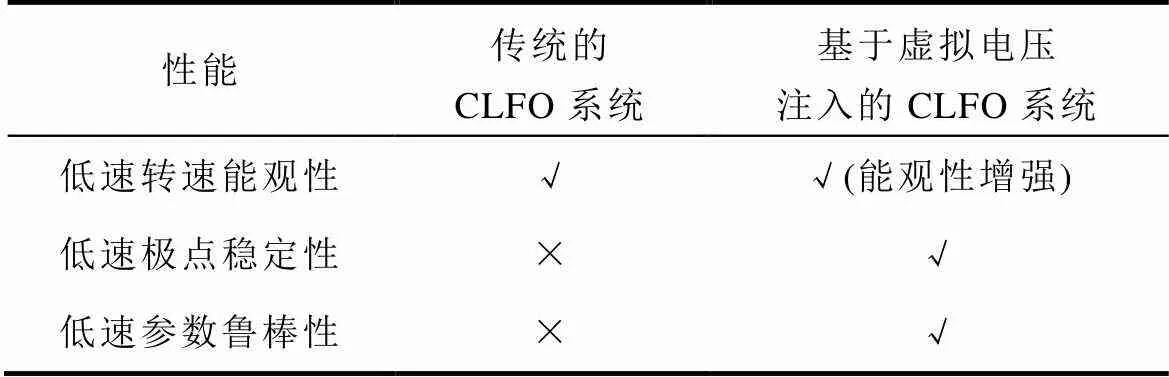
表1 虛擬電壓注入對CLFO系統的性能改進

注：“√”表示性能理想；“×”表示性能不理想。

3 實驗驗證

為驗證虛擬電壓的有效性，本文采用5.5kW的感應電機作為被測電機進行實驗驗證，5.5kW的內嵌式永磁同步電機（Interior Permanent Magnet Synchronous Motor, IPMSM）提供負載轉矩。感應電機參數見表2。

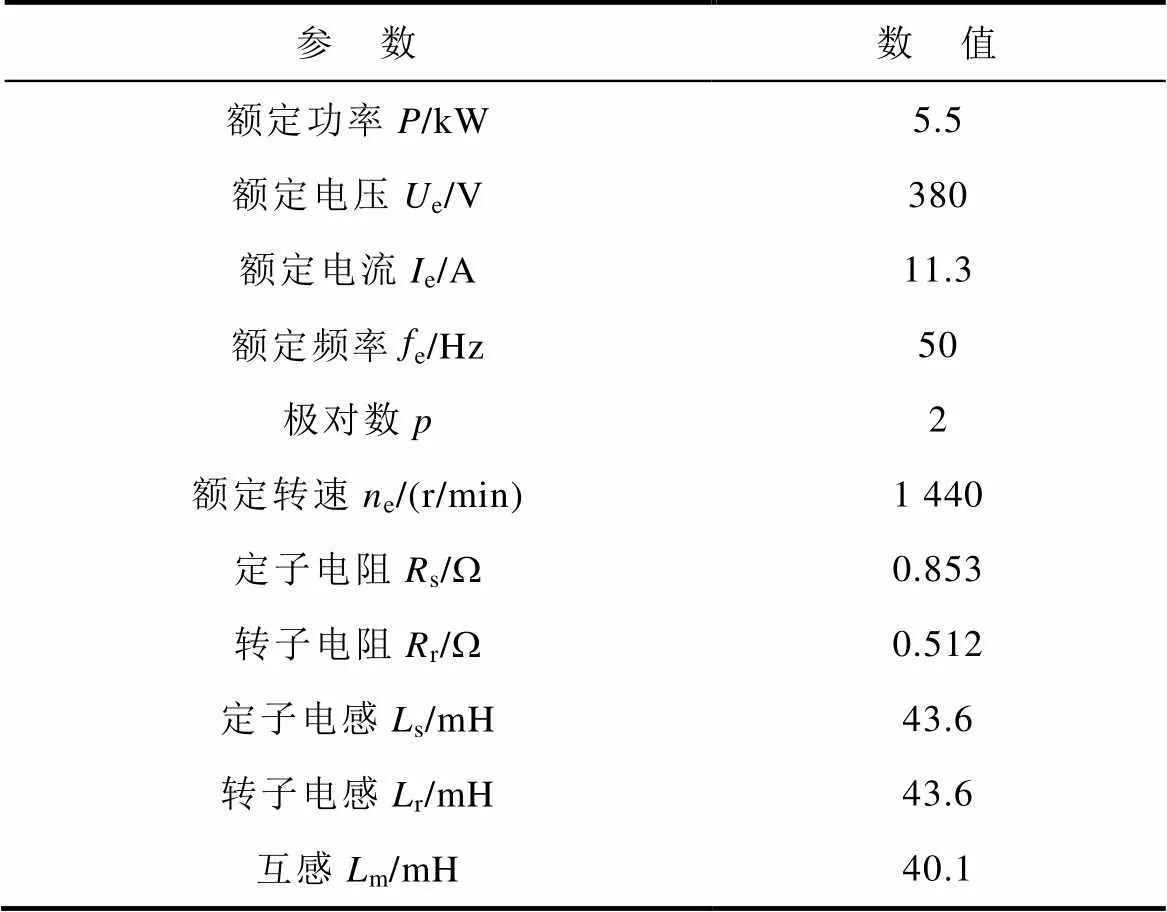
表2 感應電機參數

3.1 低速穩定性實驗

為驗證基于虛擬電壓注入的CLFO系統的低速穩定性，施加100%額定負載轉矩，給定轉子參考轉速從120r/min切換到-120r/min。當電機轉速為正時，被測電機工作在電動模式；當電機轉速為負時，被測電機工作在發電模式，實驗結果如圖8所示。

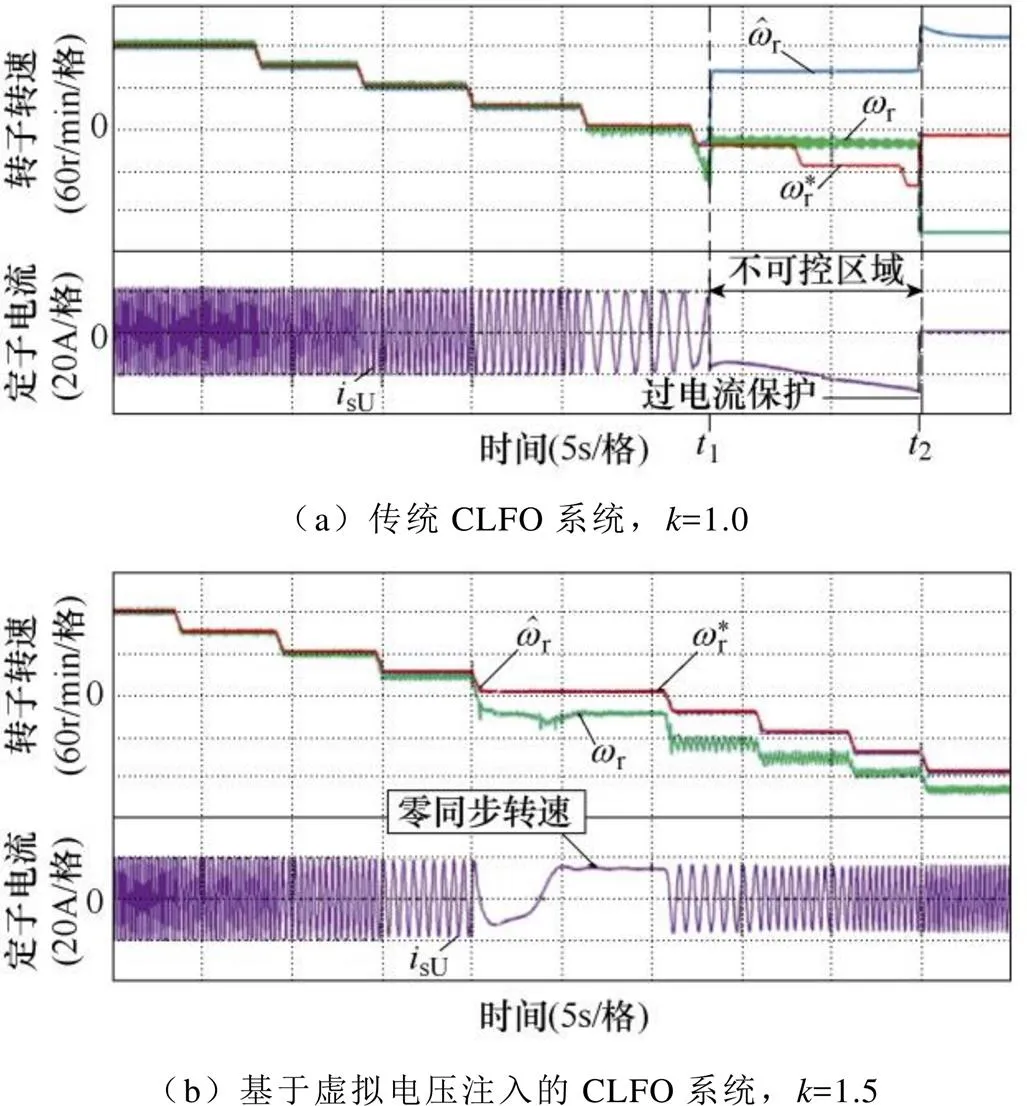
圖8 100%額定負載轉矩下的低速穩定性對比

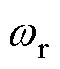
由圖8b可知，CLFO被注入虛擬電壓后，存在明顯的轉速誤差。文獻[19]詳細分析了造成該誤差的原因，并提出了相應的補償方法。為了驗證補償算法的有效性，給定參考轉速30r/min（因為該轉速下傳統CLFO系統不能穩定運行，而虛擬電壓注入法能夠保證系統穩定運行），負載由100%額定轉矩逐漸降低為-100%額定轉矩，被測電機由電動模式切換到發電模式，實驗結果如圖9所示。

從圖9可見，虛擬電壓所引起的轉速估計誤差，能夠通過補償得到消除。轉速補償前后，低速下不同負載轉矩時的轉速估計誤差（參考轉速減去實際轉速）見表3。

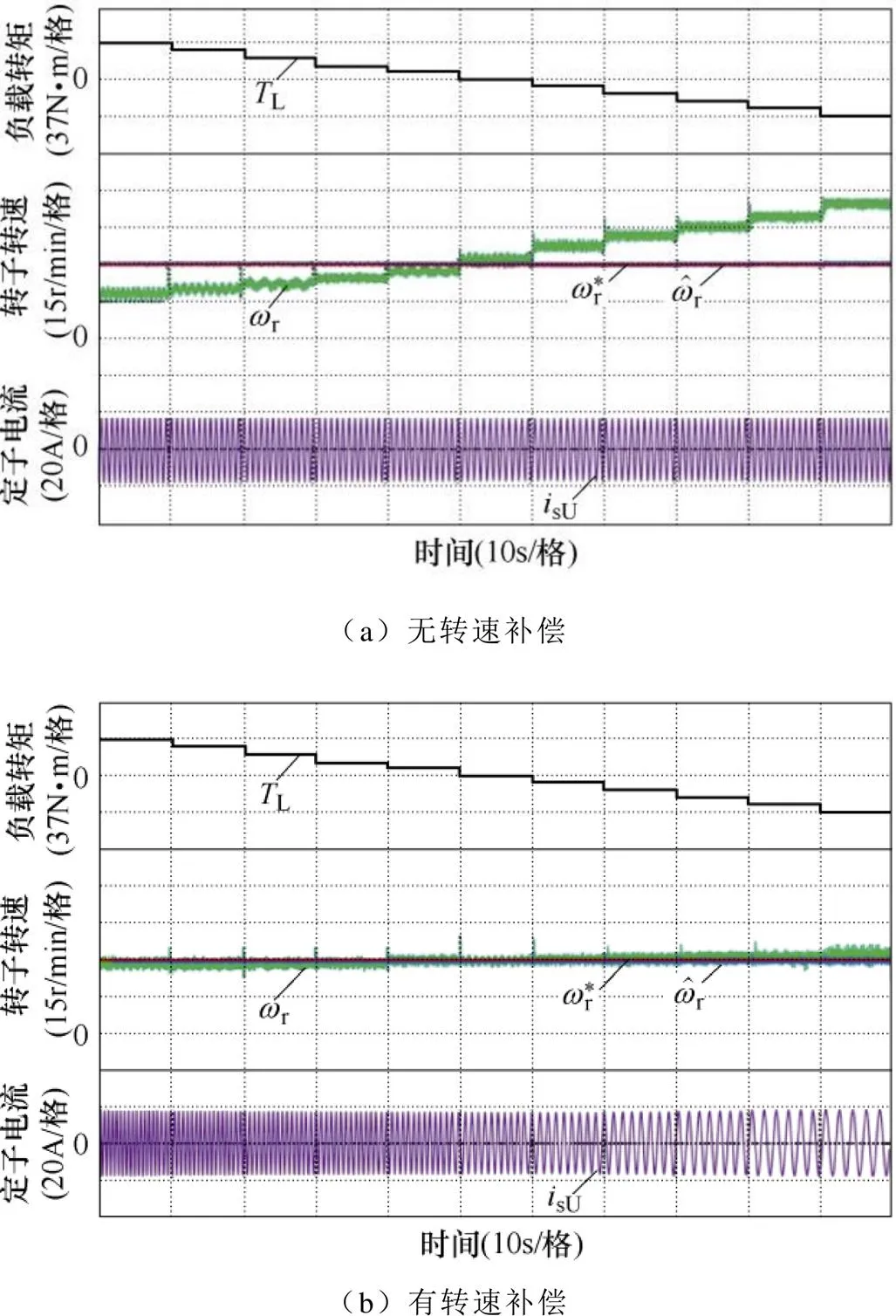
圖9 不同負載轉矩下的轉子轉速對比

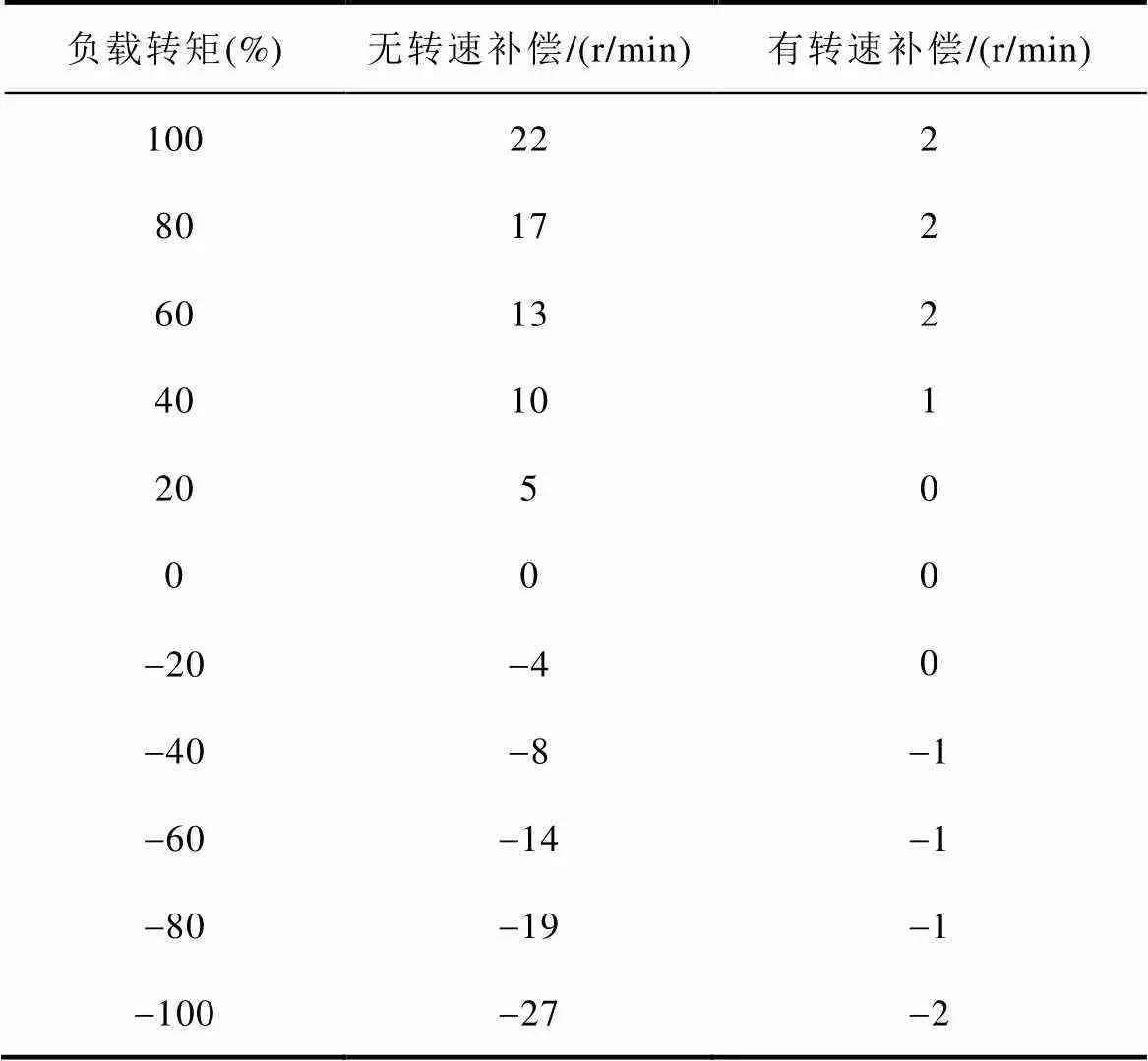
表3 低速下不同負載轉矩時的轉速估計誤差

3.2 參數魯棒性實驗

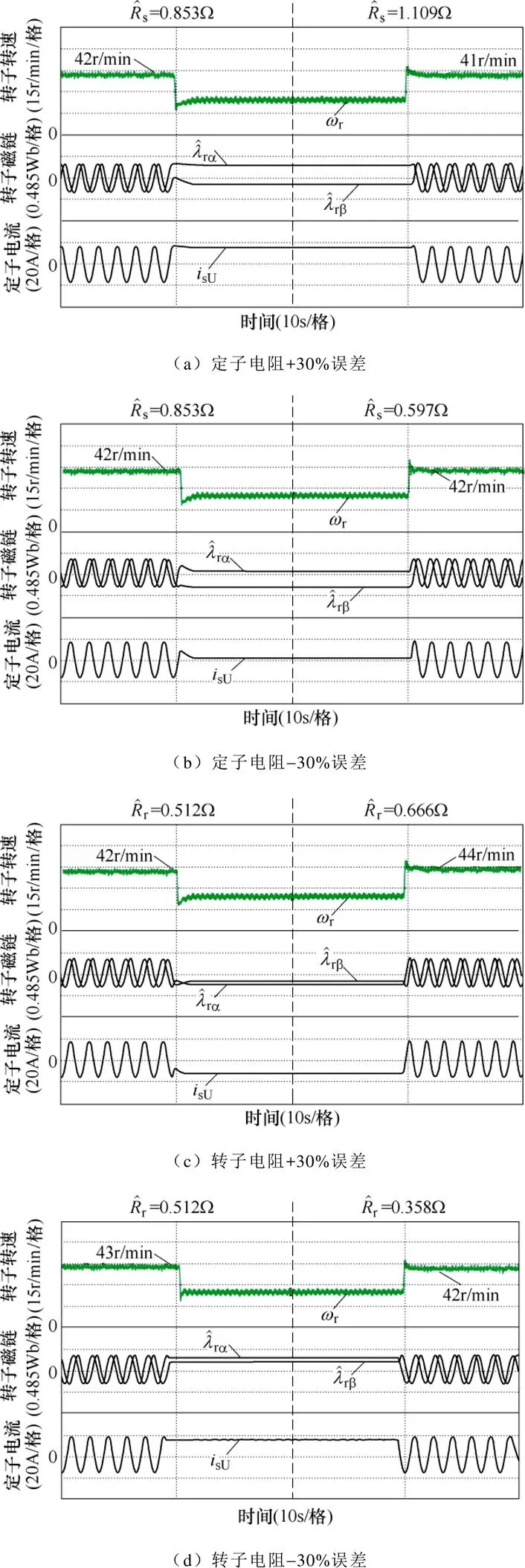
為了驗證虛擬電壓注入對系統魯棒性的改善，實驗中參考轉速從15r/min下降到0r/min，運行一段時間后，在黑色虛線處，觀測器中的電機參數發生30%階躍變化，隨后參考轉速再從0r/min上升到15r/min。在該過程中，被測電機負載轉矩始終為-100%額定轉矩，被測電機處于發電模式。實驗結果如圖10所示。

由圖10可知，在低速發電模式下，參數變化前后，系統始終保持穩定，且能長時間穩定運行在零同步轉速處。因此虛擬電壓注入改善了傳統CLFO系統的參數魯棒性問題，解決了傳統基波模型法的低速不穩定問題。

4 結論

基于CLFO的感應電機無速度傳感器矢量控制系統在低同步轉速區間具有不穩定問題。本文針對引起不穩定問題的三個因素：狀態變量能觀性、系統極點穩定性以及電機參數魯棒性進行了分析，得到了CLFO系統不穩定問題的原因。進一步地，通過虛擬電壓注入法改善CLFO系統。虛擬電壓注入法同時改善狀態變量能觀性、極點穩定性以及電機參數魯棒性問題，進而解決了系統低同步轉速區間的運行不穩定問題。對比實驗結果，基于虛擬電壓注入法的CLFO系統實現了低同步轉速下的穩定長時間運行，且具有很強的參數魯棒性。

為了分析虛擬電壓注入對無速度傳感器矢量控制系統的能觀性改進，采用小信號擾動理論推導觀測器的動態模型。

實際電機的轉子磁鏈可分別由定子電壓模型與轉子電流模型表示為

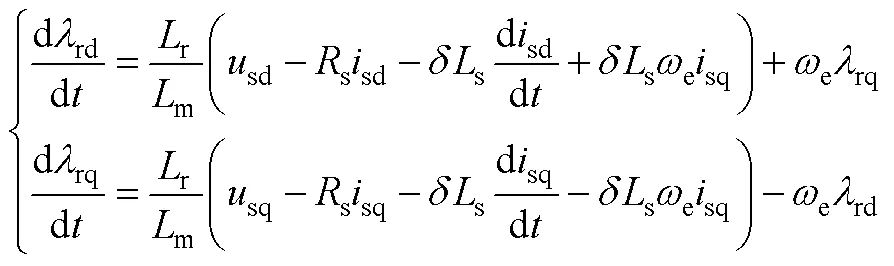
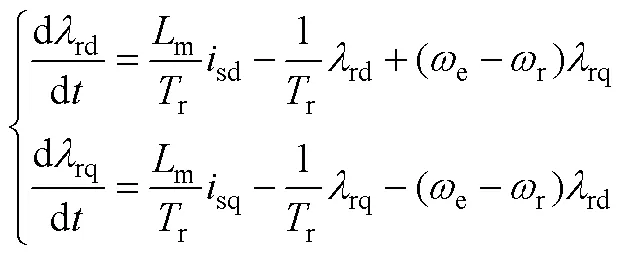
將式（A1）、式（A2）代入式（1），可以分別推導出電壓模型磁鏈估計誤差與電流模型磁鏈估計誤差為

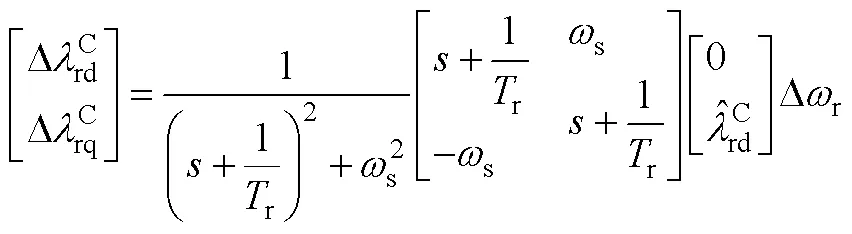
其中

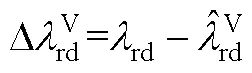
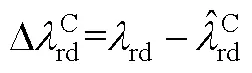
將轉速估計算法式（2）變換為

感應電機無速度傳感器驅動系統基于轉子磁鏈定向，穩態時可得

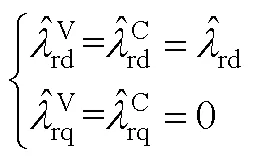
根據式（A3）～式（A6）可推導出估計轉速與轉速估計誤差及電壓的傳遞函數為

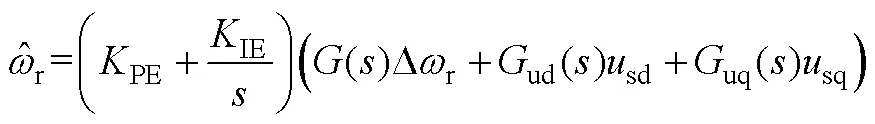
其中

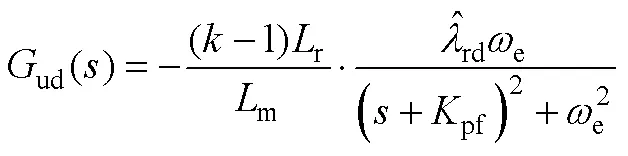
根據式（A7）可構建系統的動態模型。

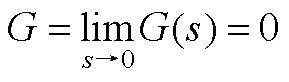
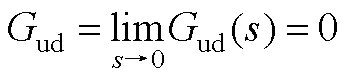
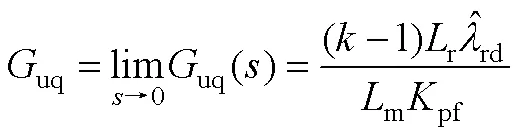
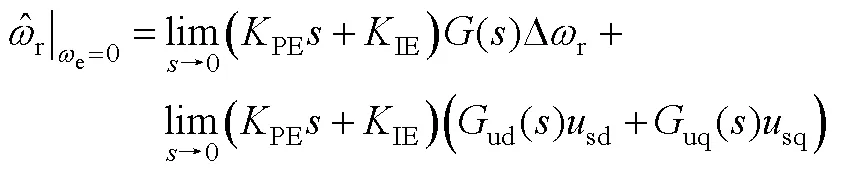
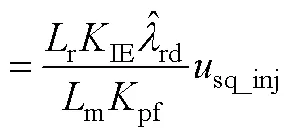
此時，估計轉速的穩態值由q軸注入電壓決定。

[1] Xu Dianguo, Wang Bo, Zhang Guoqiang, et al. A review of sensorless control methods for AC motor drives[J]. CES Transactions on Electrical Machines & Systems, 2018, 2(1): 104-115.

[2] Gao Q, Asher G, Sumner M. Sensorless position and speed control of induction motors using high- frequency injection and without offline precom- missioning[J]. IEEE Transactions on Industrial Electronics, 2007, 54(5): 2474-2481.

[3] Staines C S, Caruana C, Asher G M, et al. Sensorless control of induction machines at zero and low frequency using zero sequence currents[J]. IEEE Transactions on Industrial Electronics, 2006, 53(1): 195-206.

[4] Metwaly M K, Elkalashy N I, Zaky M S, et al. Slotting saliency extraction for sensorless torque control of standard induction machines[J]. IEEE Transactions on Energy Conversion, 2018, 33(1): 68-77.

[5] Wang Gaoling, Yang Lei, Zhang Guoqiang, et al. Comparative investigation of pseudorandom high- frequency signal injection schemes for sensorless IPMSM drives[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 2123-2132.

[6] 劉善宏, 楊淑英, 李浩源, 等. 基于旋轉坐標系解調的內置式永磁同步電機旋轉高頻注入法位置觀測[J]. 電工技術學報, 2020, 35(4): 708-716.

Liu Shanhong, Yang Shuying, Li Haoyuan, et al. Rotating high frequency signal injection based on interior permanent magnet synchronous motor rotor position estimation with the demodulation imple- mented on the synchronous reference frame[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 708-716.

[7] 李文真, 劉景林. 考慮磁路飽和及交叉耦合效應的內置式永磁同步電機無傳感器優化方法[J]. 電工技術學報, 2020, 35(21): 4465-4474.

Li Wenzhen, Liu Jinglin. An improved sensorless method of IPMSM considering magnetic saturation and cross-coupling effect[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4465-4474.

[8] 吳春, 陳科, 南余榮, 等. 考慮交叉飽和效應的變角度方波電壓注入永磁同步電機無位置傳感器控制[J]. 電工技術學報, 2020, 35(22): 4678-4687.

Wu Chun, Chen Ke, Nan Yurong, et al. Variable angle square-wave voltage injection for sensorless control of PMSM considering cross-saturation effect[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4678-4687.

[9] Yousefi-Talouki A, Pescetto P, Pellegrino G, et al. Combined active flux and high-frequency injection methods for sensorless direct-flux vector control of synchronous reluctance machines[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(3): 2447-2457.

[10] Maksoud H A, Shaaban S M, Zaky M S, et al. Performance and stability improvement of AFO for sensorless IM drives in low speeds regenerating mode[J]. IEEE Transactions on Power Electronics, 2019, 34(8): 7812-7825.

[11] 苗軼如, 劉和平, 杜俊秀, 等. 一種異步電機自適應線性神經元速度觀測[J]. 電機與控制學報, 2018, 22(11): 52-57, 66.

Miao Yiru, Liu Heping, Du Junxiu, et al. Speed observer of ADALINE for induction motors[J]. Electric Machines and Control, 2018, 22(11): 52-57, 66.

[12] 楊淑英, 丁大尉, 李曦, 等. 基于反電動勢滑模觀測器的異步電機矢量控制[J]. 電機與控制學報, 2016, 20(10): 23-30.

Yang Shuying, Ding Dawei, Li Xi, et al. Back-EMF based sliding mode observer for vector control of induction machine[J]. Electric Machines and Control, 2016, 20(10): 23-30.

[13] 陳闖, 王勃, 于泳, 等. 基于改進指數趨近律的感應電機滑模轉速觀測器研究[J]. 電工技術學報, 2020, 35(增刊1): 155-163.

Chen Chuang, Wang Bo, Yu Yong, et al. An improved exponential reaching law based-sliding mode observer for speed-sensorless induction motor drives[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(S1): 155-163.

[14] Yin Zhonggang, Li Guoyin, Zhang Yanqing, et al. Symmetric-strong-tracking-extended-Kalman-filter-based sensorless control of induction motor drives for modeling error reduction[J]. IEEE Transactions on Industrial Informatics, 2019, 15(2): 650-662.

[15] Jansen P L, Lorenz R D. Accuracy limitations of velocity and flux estimation in direct field oriented induction machines[C]//European Conference on Power Electronics & Applications, Brighton, UK, 1993, 4: 312-318.

[16] Vaclavek P, Blaha P, Herman I. AC drive obser- vability analysis[J]. IEEE Transactions on Industrial Electronics, 2013, 60(8): 3047-3059.

[17] Holtz J. Sensorless control of induction machines- with or without signal injection?[J]. IEEE Transa- ctions on Industrial Electronics, 2006, 53(1): 7-30.

[18] Lefebvre G, Gauthier J Y, Hijazi A, et al. Observability- index-based control strategy for induction machine sensorless drive at low speed[J]. IEEE Transactions on Industrial Electronics, 2017, 64(3): 1929-1938.

[19] Sun Wei, Wang Zhenyu, Xu Dianguo, et al. Stable operation method for speed sensorless induction motor drives at zero synchronous speed with esti- mated speed error compensation[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(11): 11454- 11466.

Induction Motor Speed Sensorless Vector Control System Based on Closed-Loop Flux Observer with Virtual Voltage Injection

（School of Electrical and Electronic Engineering Huazhong University of Science and Technology Wuhan 430074 China）

For many years, the instability problem of the induction motor speed sensorless vector control system in the low synchronous speed range has not been solved. It results from the unobservable system state variables, the unstable pole distribution and the poor robustness of the motor parameters. If and only if the three problems are solved simultaneously, the instability problem in the low synchronous speed range can be solved. In this paper, a virtual voltage injection method is adopted based on the classical closed-loop flux observer to improve its stability in the low speed range. Different from the traditional high frequency/low frequency signal injection method, the virtual voltage is injected into the observer rather than the motor. It can solve the observability of the system state variables, the stability of the pole distribution and the robustness of the motor parameters at the same time. Finally, the stable operation of the system can be achieved in the low synchronous speed range.

Induction motor, speed sensorless, closed-loop flux observer, virtual voltage injection

TM346+.2

10.19595/j.cnki.1000-6753.tces.L90249

國家自然科學基金（51807077）和臺達電力電子科教發展計劃（DREG2018002）資助項目。

2020-07-07

2020-11-01

王震宇 男，1996年生，碩士研究生，研究方向為交流電力傳動。

E-mail: wang_zhenyu@hust.edu.cn

孫 偉 男，1961年生，博士，講師，研究方向為交流電力傳動和電力電子控制理論。

E-mail: sunwei77@hust.edu.cn（通信作者）

（編輯 陳 誠）